一种带对数二次邻近项定制临近点的算法
李思吉,申 远
(南京财经大学 应用数学学院,江苏 南京 210023)
对于传统的带有线性等式约束的凸优化问题
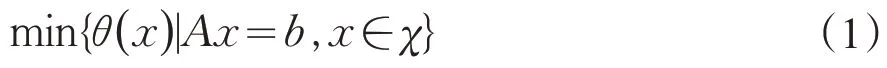
其中θ(x) :Rn→R 是一个凸函数。A∈Rm×n,B∈Rm,χ⊆Rn是非空闭凸集。问题(1)的解集用χ*来表示,并且假设χ*非空。这是一个简单的1-block凸优化问题,很多实际问题如压缩传感、图像处理、机器学习等,都可以转化成问题(1)的形式来求解。
处理问题(1)的算法有很多,最基础的是增广拉格朗日方法(ALM),是由Magnus 等[1-2]于1969 年提出。增广拉格朗日函数将约束条件合并到目标函数中,在拉格朗日函数基础上添加了一个惩罚项,问题(1)的增广拉格朗日函数为
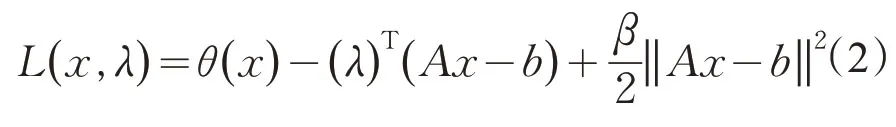
相应的增广拉格朗日方法的迭代格式如下

其中λ∈Rm,是拉格朗日乘子,x∈χ,β>0 是线性约束的罚参数。
另一个处理线性凸优化问题的有效方法是邻近点算法(Proximal Point Algorithm,PPA),该方法最早是由Moreau在1965年提出来的[3]。1976年,Rockafellar指出ALM方法和PPA方法之间的关系:ALM方法是应用到模型对偶问题上的PPA方法[4]。1999年,Alfred 论证了ALM 算法与PPA 算法之间的关系[5],但是在该论证中并没有提及PPA 算法的收敛率。2019 年,顾国勇等对经典PPA 算法进行了严格的证明,并得出该算法具有次线性收敛率[6]。
然而经典PPA算法局限于处理无约束优化问题,要处理带约束的问题就需要对它进行改进。2009年,何炳生提出带有二次邻近项的LPPA算法[7];2013年,何炳生等又提出了可以处理带有线性等式约束的定制邻近点算法(Customized Proximal Point Algorithm,简称CPPA方法),通过数值实验显示当目标函数简单时CPPA方法比ALM方法更加高效[8]。
求解问题(1)的CPPA方法的迭代格式如下
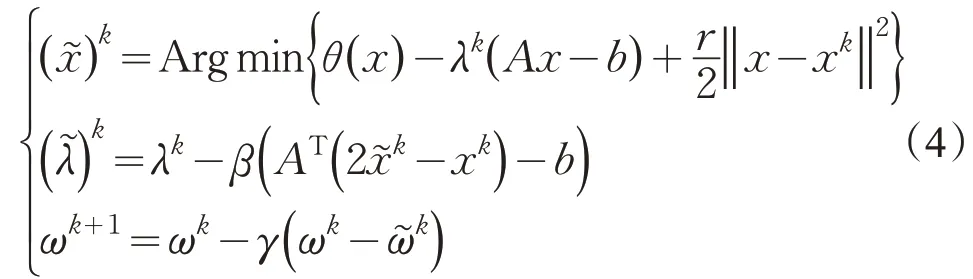
其中x∈χ,ω:=(x,λ)T,是二次邻近正则项。2014 年,顾国勇探讨了CPPA 方法的更多细节[9];2020年,邓康等提出了gCPPA方法与eCPPA方法[10]。这些方法的共同特点是都带有会使子问题复杂二次邻近正则项,尤其当变量x≥0 时,带有二次正则项的CPPA 子问题更不容易求解。对于子问题不易解的问题,可以运用对数二次邻近项(logarithmic-quadratic proximal terms,LQP)替换二次正则项,利用LQP良好的内点性质和可分性质,极大地降低了求解难度。LQP 是由Auslender 在1999 年提出的[11],之后在求解两块的分离结构变分不等式问题上得到了广泛的应用,例如文献[12]通过将LQP 和ADM方法结合,利用LQP项的内点性质降低子问题的复杂程度。2014 年,Bnouhachem 将LQP-ADM 扩展,提出了不精确的LQP-ADM 方法[13];2020 年,他又进一步提出了解决3块可分离结构变分不等式的下降LQP-ADM方法[14]。
本文主要考虑的问题是求解变量非负的带有线性等式约束的凸优化问题
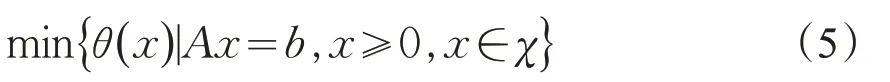
其中θ(x) :Rn→R 是一个凸函数。A∈Rm×n,B∈Rm,χ⊆Rn是非空闭凸集。我们将LQP与CPPA算法结合,提出一种新算法——LQP-CPPA方法,该方法用LQP 正则项代替传统的二次邻近正则项,使它的每个子问题都可解并且证明此算法的全局收敛性。本文的LQP-CPPA 方法利用LQP 项降低了CPPA子问题的求解难度,并且将非负约束的优化问题转化为无约束问题。
1 预备知识
1.1 对数二次邻近正则项(LQP)
对任意的z∈,LQP正则项定义为

关于引理1的证明见文献[8]。
1.2 等价的变分不等式
由问题(1)的一阶最优条件得到,求解问题(1)等价于求解
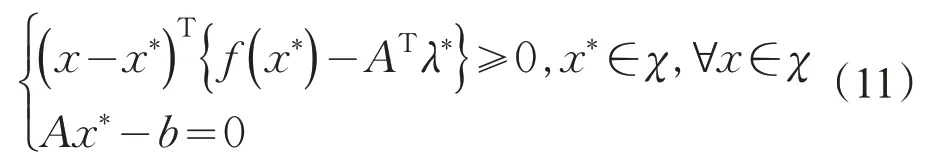
其 中f(x*)∈∂θ(x*),并且通过令u=(x,λ)T,F(u)=(f(x)-ATλ,Ax-b)T和Ω=χ×Rm,式(11)可以写成等价的变分不等式问题(VI(Ω,F)):
∀u∈Ω,找到u*∈Ω和f(x*) ∈∂θ(x*),使得(u-u*)TF(u*)≥0 成立。
我们用LQP 正则项去替换式(4)中的二次邻近项,得到新的生成预测点的迭代格式(12)。
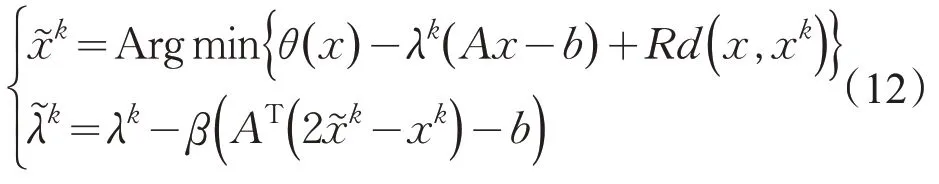
2 对于求解变分不等式问题的LQP-CPPA方法
Step1通过求解非线性方程得到预测点

Step2更新拉格朗日乘子
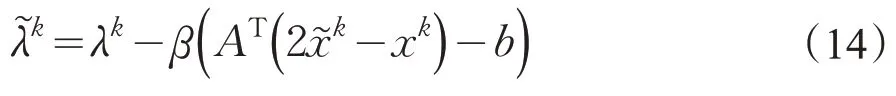
Step3生成校正点

3 新算法的一些重要性质
在证明新算法的全局收敛性之前,我们先证明一些简单的引理,这些引理将在证明新算法的全局收敛性时起到重要的作用。
定理1关于给定的xk由新算法生成的新的迭代点xk+1,对于任意的x*∈χ*,得到

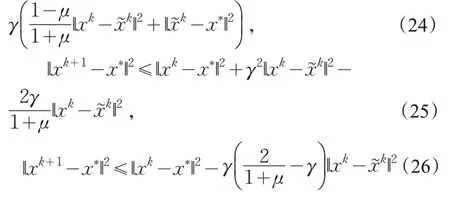
证毕。定理1 说明,由新算法生成的序列{xk}是Fejer单调的。
定理2对于给定的λk,由新算法生成的λk+1满足对任意的λ*∈Λ*,有

证毕。定理2说明,由新算法生成的序列{λk} 也是Fejer单调的。
定理3对于给定的uk,由新算法生成的uk+1对于任意的u*∈Ω*,有
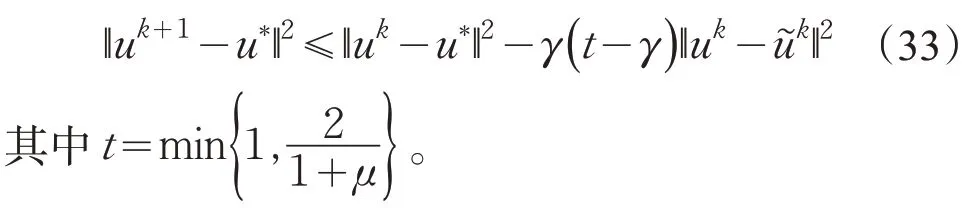
证明:由u的定义,有

将定理1和定理2应用到式(34)中,得到

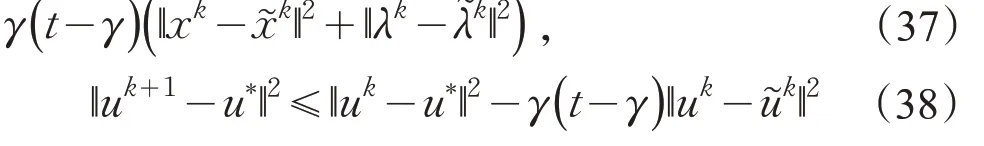
证毕。定理3 说明,由新算法生成的序列{uk}是Fejer单调的。
4 全局收敛性
定理4由LQP-CPPA 算法生成的序列{uk} 收敛到某个u∞,其中u∞是式(11)的解。
证明:由定理1-3,序列{xk},{λk},{uk} 都是有界的,并且
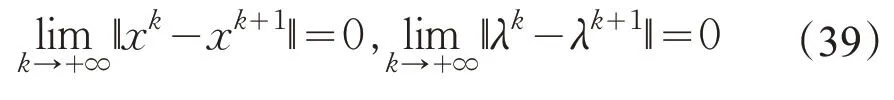
另一方面,有
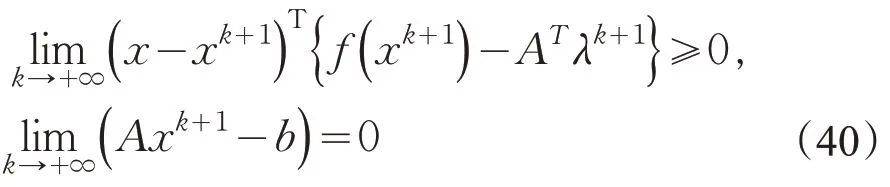
并且由有界序列必有收敛子列知{uk}至少有一个聚点,令u∞是{uk} 的一个聚点,则存在子列收敛到u∞,这样在式(40)中代入k=kj-1,有
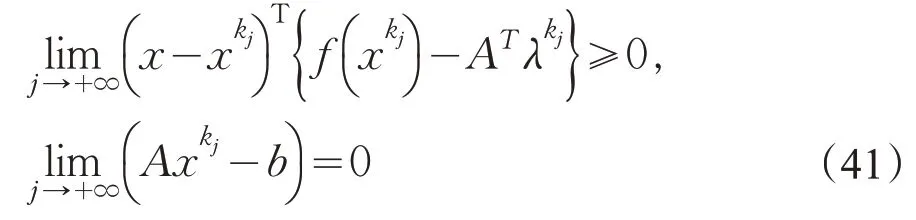
令j→∞对两端取极限,由极限的保号性有
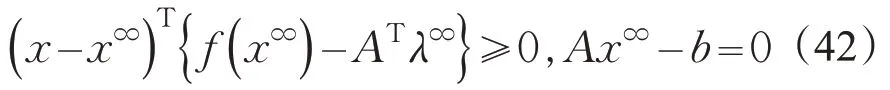
这是式(11)的解,又因为定理3对所有解集中的点都成立,所以有
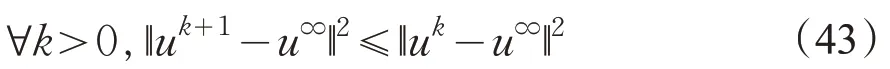
因此,序列{uk}收敛到u∞,并且u∞是式(11)的u∞解,(x∞,λ∞)是VI(Ω,F)的解。这样,就得到了算法LQP-CPPA的全局收敛性。
5 结论
本文主要考虑解决变量非负的带有线性等式约束凸优化问题的算法,通过将传统的CPPA 方法中的二次正则项替换为LQP 项,将传统的CPPA 方法与LQP 方法相结合得到新的解决变量非负的带有线性等式约束凸优化问题的LQP-CPPA 算法,新算法求解时的子问题中不再含有二次项,而是含有非线性项,使得需要求解的子问题变成了解一个非线性方程,将变量非负的约束转为无约束,这样克服了CPPA方法对要求变量非负的问题失灵的不足,它比带有二次项的子问题好解,并且我们证明了新算法的一些性质和全局收敛性。

