基于MATLAB的双缝干涉实验探索
马峰全,张玉叶,王 彤
(咸阳师范学院 物理与电子工程学院,陕西 咸阳 712000)
杨氏双缝干涉实验在光学发展历程中具有重大的历史意义,对双缝干涉的研究也从未间断。随着计算物理学的不断进步,使用计算软件分析物理问题的方法被越来越多的物理工作者所采用的。MATLAB因具有高性能的数值计算和可视化能力被众多物理工作者所使用,基于MATLAB研究双缝干涉现象的研究也不少。这些研究,在光强计算上,根据惠更斯-菲涅耳原理[1-2]或者双光束干涉的叠加原理[3-5]进行光强分析,并运用MATLAB的数值计算及可视化上对干涉现象进行模拟计算。从傅里叶光学的角度分析杨氏双缝干涉的光强分布,并用MATLAB进行模拟分析的文献还未发现。本文根据傅里叶光学分析了杨氏双缝干涉的光强分布,并用MATLAB对干涉光强进行模拟计算。
1 光强计算分析
如图1所示,单色平面光波垂直照射在双缝S1、S2所在平面x1(衍射屏),经过双缝传播到观察平面x(观察屏)。在光学实验中,杨氏双缝干涉实验一般采用演示的方法,利用激光光源直接照射在双缝上,根据实验环境,采用不同的观察屏(教室的墙壁、黑板等),为了肉眼能够直接观察到干涉条纹,一般情况下D的距离较大。在双缝干涉实验中,为了更好测量,取得更精确的结果,得到更清晰的干涉条纹,实验室一般用读数目镜测量条纹间距,典型的实验参数为d(mm)、D(m)、σ(mm)、b(10-4m),其中σ表示实验中干涉条纹存在区域的线度。观察屏光强的计算方法可以采用如下方法进行计算。

图1 双缝干涉光路示意图
1.1 双光束干涉光强计算
设缝S1、S2在观察屏上的光强分布为I1、I2,根据波的叠加原理[6],观察屏上光强

在实验中,为了得到更好的干涉条纹,通常控制实验光路确保I1=I2,此时干涉条纹的可见度最高,条纹的明暗对比最强,设I1=I2=I0,则
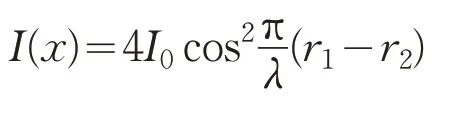
实验中,在典型实验参数的条件下,能够保证远场傍轴条件,对光程差r1-r2可以做近似计算得到

式(1)是MATLAB双缝干涉模拟计算的重要依据。
1.2 傅里叶光学光强计算
根据标量衍射理论[7-8],衍射是光振动由衍射屏后表面到观察屏的自由传播,当观察屏与衍射屏的距离远大于孔径线度并且傍轴近似条件下,可以用菲涅尔衍射计算观察面的光强分布。
1.2.1 菲涅耳衍射计算
设屏函数
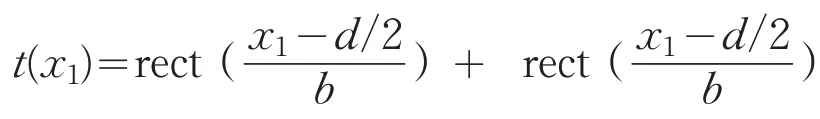
则观察屏上的光场分布为
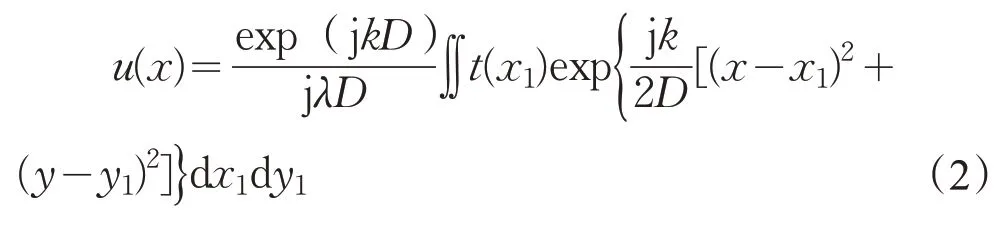
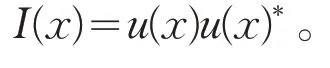
1.2.2 夫琅禾费衍射计算
在菲涅尔衍射的基础上,如果传播距离进一步增加或减小衍射孔径线度,菲涅尔衍射可进一步简化为夫琅禾费衍射。

通过不同的角度,对双缝干涉的光强分布作计算,给出了3种不同表达形式,其中式(1)(3)给出了光强分布的解析解,而式(2)只给出了积分表达式,需要采用一定的方法进行数值计算。在这3种表达式中,式(2)适用范围要比式(1)(3)的广,给出影响光强分布的因素更多。
2 仿真计算
为了更好地理解以上计算方法的差异,通过MATLAB 软件可以更直观进行分析对比。3 种方法给出的光强表达式虽有差异,但用MATLAB 软件分析计算的程序流程是相似的,其流程图如图2所示[9]。

图2 光强仿真计算流程
2.1 双光束干涉仿真计算
利用式(1),可以分析d、D及波长λ对光场的影响。设波长λ=632.8 nm,双缝间距d=1 mm,衍射屏到观察屏的距离D=2 m,观察区域线度σ=12 mm,其结果如图3所示。

图3 双缝干涉光强仿真
通过改变D、d的大小得到的光强分布如图4。从图4 分析可以得出,只要D/d的比值固定不变,其仿真结果一样,这也是目前软件分析光强分布的最常用方法。即使当缝间距d=0.001 mm,D=2 mm 时也能仿真出清晰的干涉图像,在该条件下,式(1)成立的条件已经被破坏,也能得到相对应的成果。从实验角度,在如此参数下,实验的实现是困难的,仿真结果与实验结果也是不相符的。
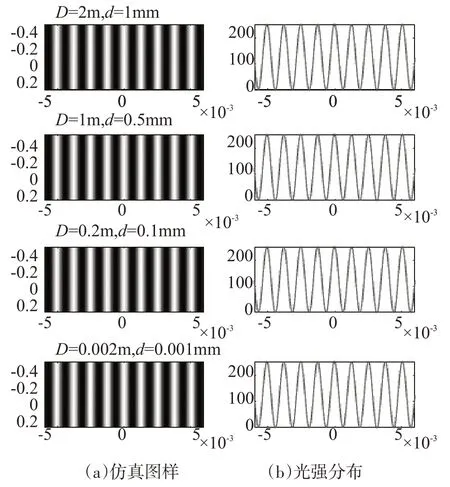
图4 不同D、d值的干涉光强仿真
2.2 夫琅禾费衍射仿真计算
设波长λ=632.8 nm,双缝间距d=1、0.5、0.25 mm,缝宽b=1、0.5、0.25 mm,衍射屏到观察屏的距离D=2 m,观察区域线度σ=16 mm,当d=b时,实际分析为单缝衍射。根据式(3)进行仿真如图5,从仿真计算结果分析与夫琅禾费单缝衍射结果相同。

图5 单缝衍射光强仿真
波长λ=632.8 nm,双缝间距d=1 mm,衍射屏到观察屏的距离D=1 m,观察区域线度σ=16 mm,改变缝宽b,其计算结果如图6所示。
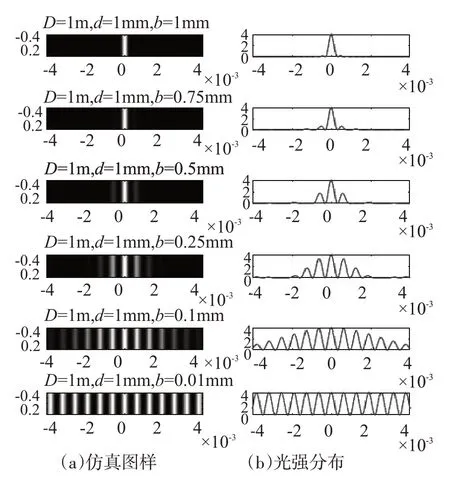
图6 不同b值的光强仿真
在固定双缝间距d及干涉距离D的前提下,改变缝宽b的前提下(1∶1,1∶0.75,1∶0.5,1∶0.25,1∶0.1,1∶0.01),可以看到随着缝宽的不断减小,单缝衍射的因素越来越强,缝间干涉的因素显示得越清晰,当缝宽与缝间距比例达到100 时,缝宽b=0.01 mm 时,其光强分布与式(1)仿真计算结果相同。从图6的光强分布曲线可以看到,随着缝宽的不断减小,单缝衍射中央亮条纹的宽度不断增加,在相同的显示区域内,能观察到的缝间干涉图像区域越大,双缝干涉效果越明显。
2.3 菲涅尔衍射仿真计算
根据标量衍射理论,式(2)也可以表示为
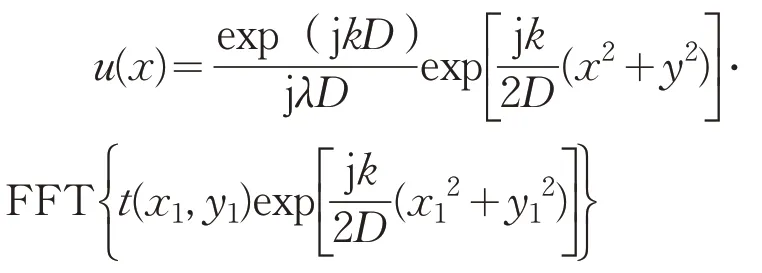
FFT{}表示傅里叶变换,可以利用软件的傅里叶变换函数而实现。
设波长λ=632.8 nm,双缝间距d=1 mm,缝宽b=0.1 mm,衍射屏到观察屏的距离D=1 m。计算结果如图7所示。结果与式(1)(3)相同。

图7 菲涅尔衍射光强仿真
保持d、b数值不变,改变D的取值,对观察屏的强度分布计算如图8所示。
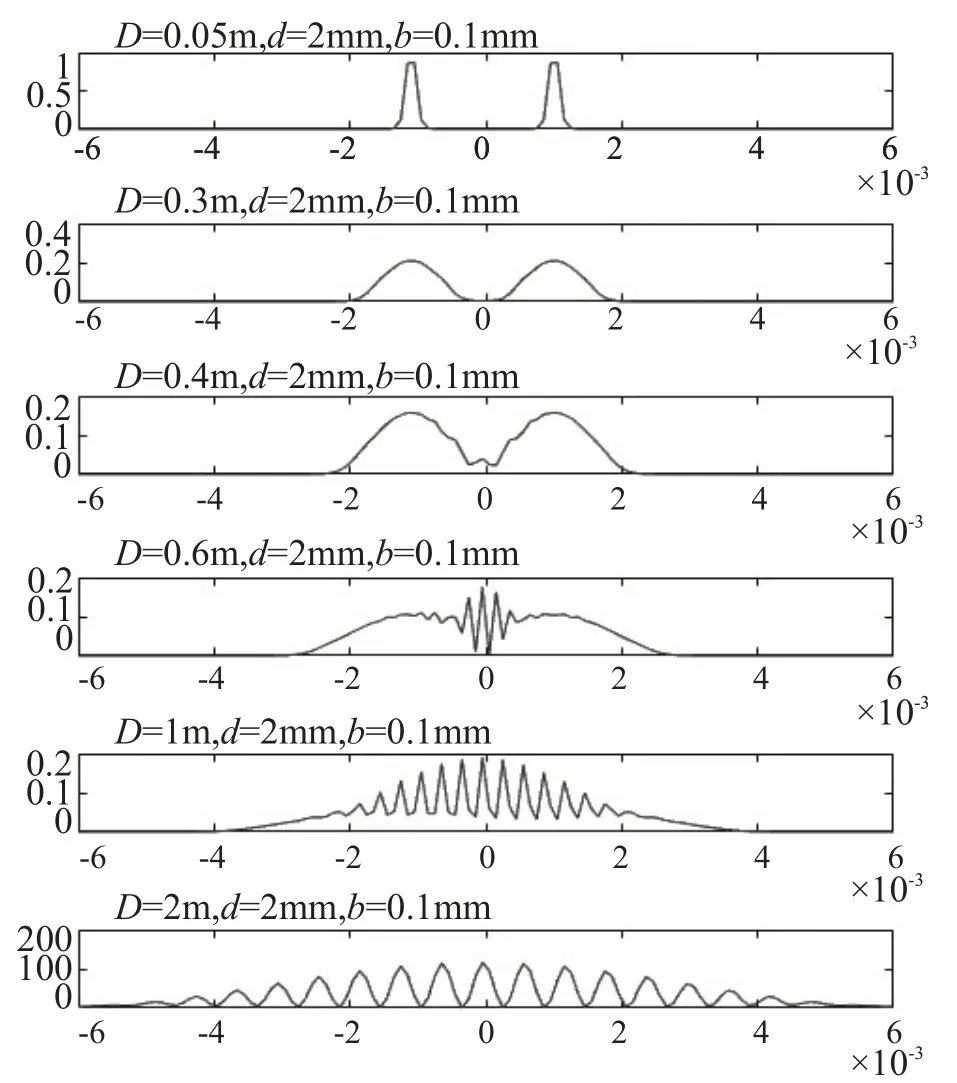
图8 不同D值的光强仿真
从图8中可以看出,当衍射距离D为5 cm时,光的传播还可以近似为直线传播,缝S1、S2发出的光波还没有相遇。随着D的增加,单缝的衍射现象越来越明显,D=30 cm时,两单缝衍射的中央条纹开始相遇,发生相干叠加,当衍射距离增加到1 m 时,干涉条纹明显,随着D值得进一步提升,条纹的可见度得到提高。从图中可以看出,干涉条纹主要集中在两单缝衍射中央条纹叠加区域,双缝干涉是单缝衍射对应中央条纹的相干叠加,干涉条纹的观察区域的大小与单缝衍射中央明纹的宽度相对应。
用该方法计算的结果与双缝干涉实验相吻合,双缝干涉实验操作一般是先找到两束光的相遇区域,当用一张白纸辅助确定相遇区域时,随着白纸与双缝之间距离的变化,白纸上光强的变化与仿真结果相一致。
3 结论
波长λ=632.8 nm,双缝间距d=1 mm,衍射屏到观察屏的距离D=1 m 时,采用不同的计算方法得到的结果相同,但是采用光程差计算的结果最为优美,与教材理想化的分析最为相符;在D=1 m时,改变d、b数值,夫琅禾费衍射计算能够清晰地得到双缝干涉是单缝衍射对多缝干涉调制的结果;在d=2 mm、b=0.1 mm时,改变D值,菲涅耳衍射计算结果与实验结果相符,更好地阐释了干涉与衍射的联系。通过仿真计算,进一步明确双缝干涉强度分布公式成立的前提条件,清楚实验结果与理论结果的差异的原因。在3种计算方法中,菲涅耳衍射计算与实际最相符,从编程的角度分析,菲涅耳衍射计算难度较大,需要考虑衍射面的尺寸及观察区域的线度,另外选择合适的采样,也是仿真计算成败的关键。

