整合分数阶等宽波动方程的所有单行波解的分类

李 钊，蒋志颖

（成都大学 计算机学院，四川 成都 610106）

许多自然科学和工程技术中的问题通常可以用非线性偏微分方程来建模。近年来，非线性偏微分方程备受关注[1-2]。对于非线性偏微分方程的研究主要有解的存在唯一性、稳定性、初边值问题下整体解的存在性和渐近性、数值解和精确解等。特别是寻找非线性偏微分方程的精确解是非线性偏微分方程研究的核心问题之一[3-5]。但是，由于非线性方程的复杂性，可能出现高阶的非线性偏微分方程或者复杂的分数阶偏微分方程。因此，无法建立一个统一的构建非线性偏微分方程精确解的方法。但是通过众多科学家的不断努力，一些行之有效的方法已经被提出，如：齐次平衡方法[6]、双曲函数展开法[7]、首次积分法[8]、平面动力系统分析法[9]和多项式完全判别法[10]等。特别是，刘成仕[11]提出了一种被称作多项式完全判别系统的新方法，能够很好地给出非线性偏微分方程单行波解的分类。同时，该方法被杜兴华等[12]进一步发展，被应用于寻找具有实际背景的非线性偏微分方程和方程组的单行波解的构造。近年来，在物理学和工程技术中，带有记忆性的分数阶偏微分方程被提出来，然而，对于物理工作者和工程研究人员亟待解决的问题是：给出这类方程的解析解（通常称为精确解）。目前，一些成熟的方法已经被提出用于构建分数阶偏微分方程的精确解，比如：（G'/G）-展开法[13]、群分析方法[14]、指数函数展开法[15]和平面动力系统分析方法[16]等。

本文利用多项式的完全判别法考虑如下整合分数阶等宽波动方程（conformable fractional equal width wave equation）[17]

其中0 ＜α≤1,和分别表示未知函数u关于时间变量t和空间变量x的整合分数阶导数，a和b为实参数。

定义1[18]设函数f:[0,∞)→R

1 方法描述

首先考虑如下的整合分数阶时间分数阶偏微分方程

其中u=u(t,x)，P是含有u的关于变量x的导数、变量t的导数、变量t和变量x的分数阶导数的多项式。

步骤1对方程（3），引入行波变换u(t,x)=u(ξ)，，其中k，c为待定常数。则方程（3）转化为非线性常微分方程

步骤2如果上述非线性的常微分方程（4），经过一系列的变换后能够约化称为如下的常微分形式

式（5）可以写成积分形式

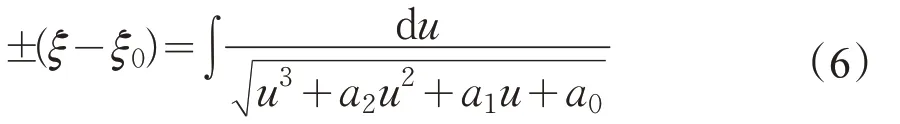
接下来，我们可以根据多项式完全判别系统获得方程（6）的解的分类。

2 整合分数阶波动方程的精确解

对方程（1）做行波变换

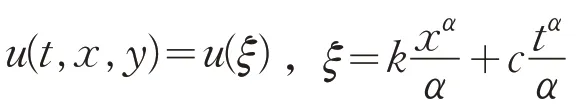
其中k和c为待定常数。则式（1）被简化为

对式（7）关于ξ积分一次

其中c1是积分常数。

在式（8）两端同时乘以u′，可得

对式（9）两端同时积分一次，化简可得

其中c2是积分常数。

令

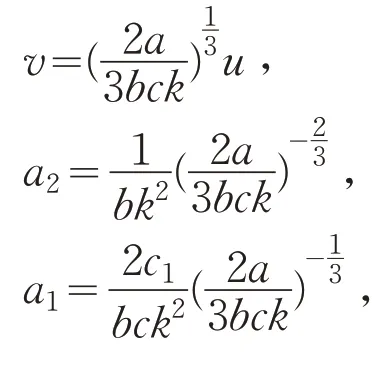
则式（10）可转化为

则式（11）的积分形式为

为了方便计算，这里记f(v)=v3+a2v2+a1v+a0，它的完全判别系统为那么根据三阶多项式的完全判别系统，可以得到式（1）的解有以下4种情况：

情况1Δ=0，D1＜0 时，即

图1 式(1)的解u1(t,x)三维图

图2 式(1)的解u3(t,x)三维图

情况2Δ=0，D1=0 时，即

情况3Δ＞0，D1＜0 时，即

当α＜v＜γ时，作变换

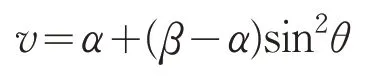
由式（12），可得

3 结论

本文给出了分数阶偏微分方程的三阶多项式完全判别法，并且利用该方法给出了整合分数阶等宽波动方程的所有单行波解的分类，这些解主要包括双曲函数解、三角函数解、有理函数解和Jacobi椭圆函数解。与文献[17]相比，本文所利用的方法是新的，并且所获得的解更加丰富。本文的完全判别法也适用于其他可化简为三阶多项式（6）的分数阶偏微分方程。