关于3级Fibonacci数的一些恒等式
杨衍婷
(咸阳师范学院 数学与统计学院,陕西 咸阳 712000)
在文献[1]中,Fibonacci 数Fn与Lucas 数Ln分别定义为

满足

其中α,β为方程x2-x-1=0 的两个不同的根。
Fibonacci 数Fn和Lucas 数Ln可分别称为2 级Fibonacci数和2级Lucas数。类似地,按照2级Fibonacci数与2级Lucas数的定义,3级Fibonacci数与3级Lucas数分别为

满足

其中α,β,γ为方程x3-x2-x-1=0 的3 个不同的根。
长期以来,关于Fibonacci 数的各种性质的研究一直是数论和组合数学中引人关注的焦点问题,包含Fibonacci数的恒等式更是国内外众多专家和学者的研究热点。杨海等[2-4]研究了二项式系数与Fibonacci 数幂的关系,得出了有趣的几个恒等式;陈国慧[5]利用初等方法以及指数函数的幂级数展开,给出了一组关于Fibonacci 数列及Lucas 数列的恒等式;Xue 等[6]研究了与二项式系数相关的广义Fibonacci与Lucas数的恒等式;吴振刚[7]研究了包含广义Fibonacci 数列倒数积的恒等式;陈斌[8]研究了广义Fibonacci 数的性质,给出了关于广义Fibonacci 数的两个恒等式。2 级Fibonacci 数的研究理论相对比较成熟,关于3级及以上高级Fibonacci数的研究较少,但是高级Fibonacci 数也是很重要的一类数论函数,应用也非常广泛,例如,庞荣波[9]研究了4 级Fibonacci数列的性质,并给出4 级Fibonacci 数在正整数分拆中的应用。本文利用3 级Fibonacci 数的生成函数,借助几何级数的和函数,研究包含3 级Fibonacci 数的恒等变换,得出了一些有趣的恒等式与同余式。
1 相关引理

引理1对于任意的实数δ,x,有

其中δx≠1,i=1,2,…。

根据数学归纳法,假设i=k时结论成立,当i=k+1 时

两边关于x求导,得

从而有

所以结论成立。
引理2对于任意的实数x,ξ,η,有

其中ξx≠1,ηx≠1,m=1,2,…。
证明:当m=1 时,
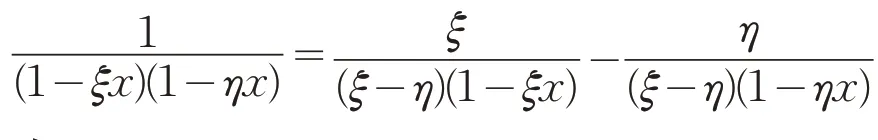
结论成立。
设m=k时结论成立,则当m=k+1 时
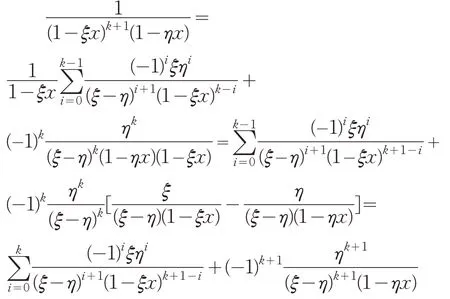
根据数学归纳法,结论成立。
引理3对于3级Fibonacci数和Lucas数,有

证明:根据3 级Fibonacci 数与3 级Lucas 数的定义与性质,有

2 主要结论
定理1对于任意的正整数a,b,n,有恒等变换

证明:基于Δ2=-44,根据引理1、引理2 和引理3,由几何级数的和函数

其中


推论1对于任意的正整数n,有同余式

证明:由定理1可得。
定理2对于任意的正整数a,b,c,n,有恒等变换

证明:由几何级数的和函数


由引理1 和引理2,将上式每一项展开成幂级数,然后对αn,βn,γn的系数分别组合合并同类项,根据根与系数的关系,将αn,βn,γn的系数表示成α,β,γ的幂(指数可以为负)的多项式,基于Δ2=-44,得

由引理3和3级Fibonacci数的递推关系可得结论。
推论2对于任意的正整数n,有同余式

证明:由定理2可得。
3 结论
Fibonacci 数与Lucas 数长期以来是研究的热点问题,在已有研究结果的基础上,本文利用三阶线性递推数列的基本性质,研究包含3 级Fibonacci 数的恒等变换,得出了一些有趣的恒等式与同余式,丰富和推广了2 级Fibonacci 数列的相关结论,为高级Fibonacci数列的研究提供一定的帮助。

