浅谈在数学课堂中促进学生深度学习的教学策略
高清文
深度学习,是指在教师的指导下,学生围绕具有挑战性的学习主题,全身心参与、体验成功、获得发展的有意义的学习过程。如何践行深度学习的数学课堂?笔者以为应创设激发学生认知需求的情境,注重知识与方法之间的联系,引导学生自主探究,让学习真正发生,发展学生的核心素养。
一、创设情境,促使深度学习成为可能
情境创设,让学生置身于求知的环境中,对于学生走向深度学习大有裨益。在数学教学中,教师应以教学内容为本,抓住学生的心理特征,通过设置具有认知冲突的问题情境,激发学生的学习兴趣,使之处于心意求而未得,口欲言而不能的状态,真正进入到学习活动中,深度学习的发生才能成为可能。
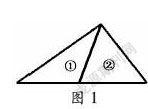
例如,在教学“三角形的内角和”时,通过学前调研,学生对“三角形的内角和是180度”都有一定的认知,于是教师创编教材情境:课件出示一个三角形,教师问:“它的内角和是多少度?”学生异口同声:“180度。”紧接着教师在这个三角形中做了一点小变化(如图1)。紧接着,教师问:“这时①号三角形的内角和是几度呢?”部分学生脱口而出:“90度。”有学生紧随其后,立马反驳:“不对,是180度。”教师问:“那么,②号三角形呢?”仍有学生坚持说180度,但明显底气不足了,更多的学生陷入了沉思之中。不一会儿,一个个疑问冒了出来:一个三角形的内角和是180度,分成几个更小的三角形后,每个三角形的内角和还是180度吗?是不是任意三角形的内角和都是180度呢?带着这些疑惑学生自然而然会进入深度探究。
原来的学习情境:“画几个三角形,并量一量、算一算它们的内角和是多少度?”学生只是被动地验证,并没有主动思考,也不存在认知冲突。改编后的学习情境,与学生的原有认知相冲突,疑惑重重,驱使学生进入深度学习。
二、注重关联,促使深度学习自然发生
数学知识是螺旋上升的,它们之间具有一定的联系性。因此教师可以把结构相同、相近的数学知识整合在一起进行教学,利用知识之间的联系开展教学活动,激发学生主动探究,促使学生深度思考,深度学习才得以自然发生。
例如,在学习“运算定律”这一单元时,我们可以做如下整合:把加法交换律和乘法交换律放在同一个课时进行教学。先教学加法交换律,课上让学生举出大量的例子,引导学生观察发现,自主建构加法交换律的知识结构,然后教师抛出问题:“交换两个加数的位置,和不变,这种关系是否也存在于其他运算中呢?”学生兴趣盎然,把学习加法交换律的方法投入到乘法交换律的探索中,很快发现了它们二者之间的相同之处,清晰地看到两个运算定律中的相同表征——参与运算的两个数的位置变了,但结果不变,深刻理解了交换律的结构。还有的学生举出例子:40-6=34,6-40≠34,40÷8=5,8÷40≠5。这说明除法和减法没有交换律。还可以把“连减、连除”这两课整合在一起,借助两者之间的联系,学生很容易就掌握了这两类简便运算。
以上案例中,教师把知识相似的教学内容整合在一起,让学生更充分地体会知识间的整体联系,感悟变与不变的数学思想,加深了学生对加法交换律和乘法交换律“等值变形”模型的理解,构建交换律的知识框架。在思辨和钻研中,学生的学习不断深入。
三、体验操作,促使深度学习落地生根
对于新知的学习,只有学生自身主动参与、体验操作,才可能是有效的。学生在动手实践操作中,手脑并用,充分调动各种感官,让思维在指尖绽放,让深度学习落地。
例如,在教学“不规则物体的体积”时,笔者提前布置了探索性作业:怎样测量一个土豆的体积?试一试,做一做,把你的想法、做法记录下来。笔者没有要求学生提前预习教材,怕这样会限制了他们的思维,只是把这个核心问题抛给了学生,让学生自己去思考、去创造。第二天,学生展现出了一节绝妙的生本课堂,除了常规的排水法,还有各种意外的精彩,学生的测量方法如下。
方法一:迁移求不规则图形面积的方法,先在这个土豆上面切出一个近似的长方体,量出长、宽、高,利用公式计算出它的体积,再把剩下的土豆尽可能地堆成一个长方体,估算出它的体积,最后把两者的体积相加。
方法二:先称出这个土豆的重量,然后切出1立方厘米的小块,称一下這1立方厘米有多重,再用除法计算出整个土豆的重量里包含了几个1立方厘米土豆的重量,也能求出土豆的体积。
方法三:把土豆蒸熟了捣成泥,装在一个长方体的容器里,使它变成一个长方体,利用长方体的体积公式就能求出土豆的体积。
方法四:准备两个大小一样的杯子,若干个1立方厘米的小正方体。在这两个杯子里装入同样多的水,一边放入土豆,一边放入1立方厘米的小正方体,直到两边水面的高度大致一样,最后数一数一共有多少个1立方厘米。
本课的学习中,教师给足了学生动手操作的时间,学生善用不同的工具,且运用了求不规则图形面积的方法、等积变形的原理、天平原理测量出了土豆的体积。对不规则物体体积的测量方法有了自己的理解,在如此厚重的操作实践活动中,充分感悟数学知识的本质,使知识学习从浅度走向深层。
四、拓展延伸,促使深度学习漫溯深处
深度学习需关注学生的认知延伸,教学中,不能局限在某一节课或某一个知识点上,而是要立足于原有教材,同时拓宽教材的深度和广度,对教学进行系统化、层次化的设计,抓住原有知识的延伸点进行拓展,使学生走向更广阔、更深刻的自我思维、自我探究的空间,促使深度学习持续发展。
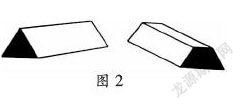
例如,在教学“立体图形的体积”时,梳理完立体图形的体积公式的推导过程后,观察发现,除了圆锥,其余图形都可以用底面积乘高来计算。紧接着教师出示课件(如图2),引导学生思考:该如何计算它们的体积?小组讨论后得出,也是用底面积乘高,因为这些立体图形可以看做是由若干个底面积叠加起来的。此时教师结合课件动态演示,学生观察由面到体的过程。教师继续追问:“你认为什么样的立体图形,体积可以用底面积乘高来计算?”学生一下子就明白了,不管什么样的立体图形,只要上下两个面完全相同,就可以用这个公式来求出体积。
综上所述,课堂上要实现学生的深度学习,教师应优化数学学习环境,关注数学知识、数学方法之间的联结,注重学生的体验与探究,鼓励学生进行深度拓展,才能使深度学习真正发生。
(作者单位:福建省厦门市同安区莲花中心小学)
——特级教师周卫东《乘法交换律》教学赏析
——特级教师周卫东苏教版四下《乘法交换律》教学赏析

