芯片级节流制冷器换热器结构多目标优化研究

童 欣，邱 杰，李家鹏，槐 阳，陈俊元，谢坤圆

（昆明物理研究所，昆明 650223）

0 引言

近年来，芯片行业发展迅速，小型化和集成化成为主要发展趋势，广泛应用于生物、光学和IT等领域[1]。随着芯片体积的缩小，适配的制冷系统也需相应缩小。芯片级节流制冷器的体积比常规节流制冷器小一个数量级左右，最早由美国斯坦福大学Little等[2-4]于20世纪70年代发明。首次采用了微加工技术，在材料表面加工出微米级的细微槽道，构成了高、低压换热器以及节流区域，并采用键合工艺进行组装密封。

芯片级节流制冷器在国外已经较为成熟，美国MMR公司推出了一系列制冷量为25～250 mW的产品，主要应用于半导体霍尔效应和塞贝克效应等检测仪器、CCD阵列芯片以及光学器件中[5]。荷兰TWENTE 大学 Lerou等[6-9]、Derking等[10-11]和 Haishan等[12-15]也对芯片级节流制冷器进行了广泛深入的研究，提出了由点阵组成的高、低压侧换热器结构，如图1[15]所示。此种结构的MMR可根据不同工况需求调整尺寸和制冷量，以双级制冷方式达到28 K制冷温度。MMR能够与微型热电制冷器进行耦合，在实现相同制冷量的同时有效降低所需的气源压力。

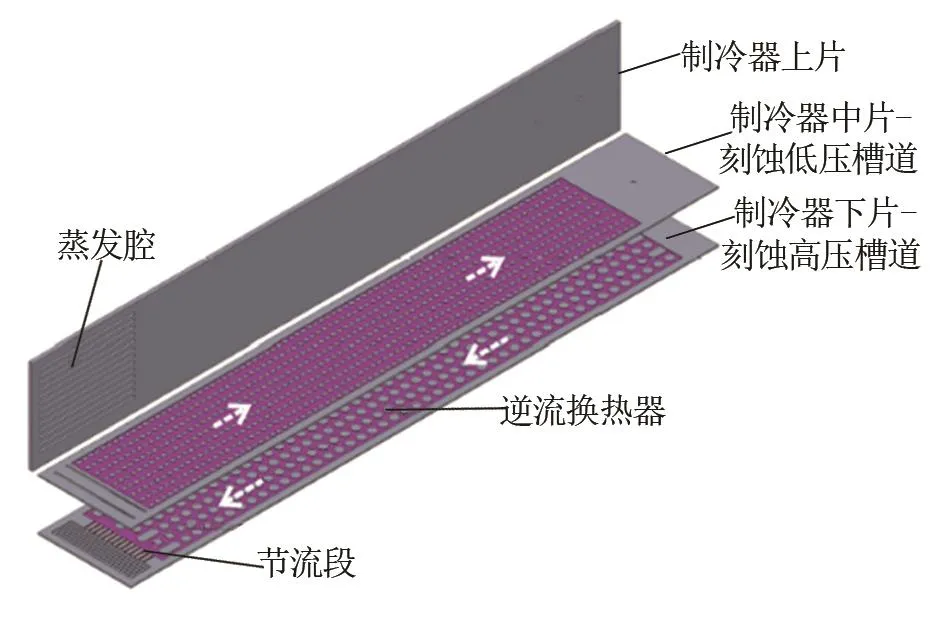
图1 TWENTE大学芯片级节流制冷器Fig.1 MMR made by TWENTE university

图1中的逆流换热器的流动和换热性能对制冷器整体性能起到至关重要的作用。文献[8]对图2所示的不同形状的换热器进行了实验研究，发现菱形和正弦型换热器拥有最佳的流动性能，然而综合考虑制造加工难度以及换热性能，最终采用了圆形点阵的方案，圆形点阵换热器的进一步优化未见报道。由于MMR结构微小，制造难度较大，数值模拟是优化其性能的有效方法。

图2 MMR不同形状的换热器结构Fig.2 Different shape of heat exchangers of MMR

由于MMR最大尺寸为60 mm，最小尺寸仅为1 μm，差距巨大，无法对整体MMR进行建模。本文对高、低压侧换热器的若干柱体组成的换热单元进行参数化建模，使模型的所有几何参数均为自变量结构参数的函数，生成结构计算实验点。然后使用CFD-Fluent进行数值计算，得到该结构的流动和换热性能数据。最后采用CCD优化算法、Kriging响应面以及多目标遗传算法优化方法对MMR换热器的努塞尔数Nu以及摩擦因子f进行优化，分别得到高压侧和低压侧换热器的理论最佳结构，并对最佳结构进行了数值计算验证。

1 MMR换热器的计算模型及数值模拟方法

1.1 计算模型的建立

为了对计算结果进行有效验证，高、低压换热器计算模型的建立和几何规律采用文献[15]中的结构，如图3（a）所示。计算模型采用参数化建模，模型自变量结构参数为柱体底部圆直径Dpillar以及沿流动方向相邻柱体间距Sspace，当自变量结构参数发生改变时模型也会随之发生改变，如图3（b）（c）所示。

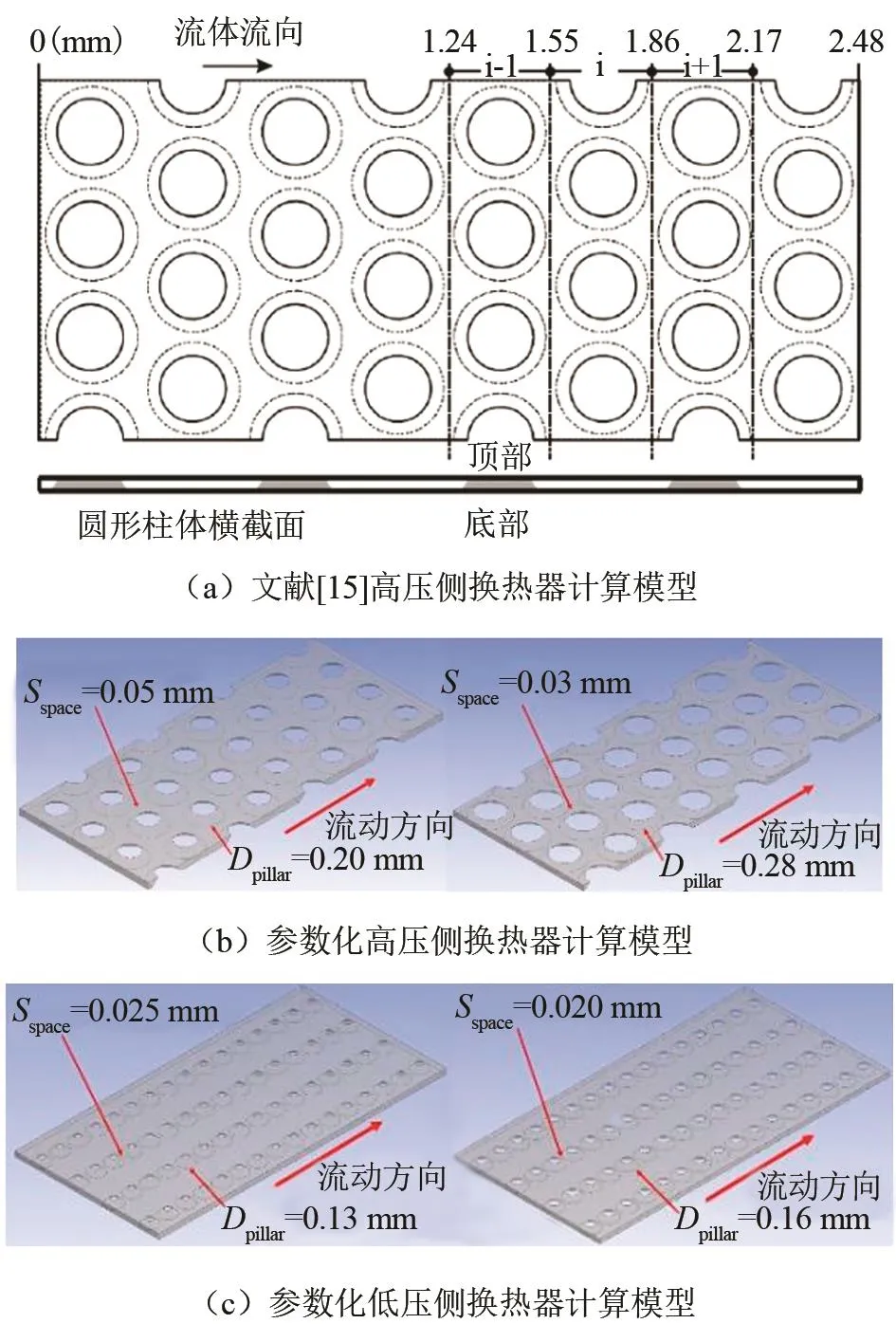
图3 MMR换热器的计算模型Fig.3 Calculation model of MMR heat exchanger

1.2 基本方程和数值方法

由于MMR换热器尺寸微小，流体在换热器内无法充分发展为湍流，因此采用层流模型进行计算，基本方程包括质量、动量和能量方程，表达式如下。

连续性方程：

式中：v为速度矢量，m·s-1；T为静态温度，K；ρ为流体密度，kg·m-3；p为静压，Pa；μ为流体分子黏度，Pa·s；cp为流体比热，J·kg-1·K-1；λ为流体导热系数，W·m-1·K-1；ϕ为湍动能耗散项。在层流模型中ϕ可忽略不计。

计算模型物性参数和边界条件设置为：高、低压侧换热器流体均采用氮气作为工质，物性在Refprop中查取，换热器中流动计算过程按照工质物性恒定进行；高压侧换热器进口氮气设置为300 K以及8 MPa，低压侧换热器进口氮气按中波红外探测器的典型工作温度97 K以及压力0.6 MPa进行设置；因模型大小会随自变量结构参数改变，计算模型进口处采用速度进口边界条件以保证在模型变换时进口雷诺数Re变化不大，高压侧换热器进口速度为0.57 m/s，低压侧换热器进口速度为0.9 m/s；模型出口采用背压为0的压力出口边界条件；高压侧换热器采用上接触面和柱体表面定壁温，低压侧换热器采用下接触面和柱体表面定壁温边界条件，以模拟实际MMR工作时高、低压侧换热器通过中间制冷器片进行导热换热的状态；壁温与流体温差设置为5 K，即高压侧换热壁面为295 K，低压侧换热壁面为102 K，其余壁面均按绝热面处理；所有壁面均设置为无滑移标准壁面函数，压力-速度耦合采用SIMPLE算法，动量和能量方程均为二阶迎风格式，各项残差均设置为1×10-6。采用以上边界条件计算得到的高压侧换热器中部平面温度分布云图如图4所示（模型结构参数见3.1节中的初始结构），模型最右边温度出现分布不均区域，原因为数值计算时出口处压力计算值与背压存在少量不匹配引发的回流现象，该区域面积较小对换热器整体性能评价影响不大。

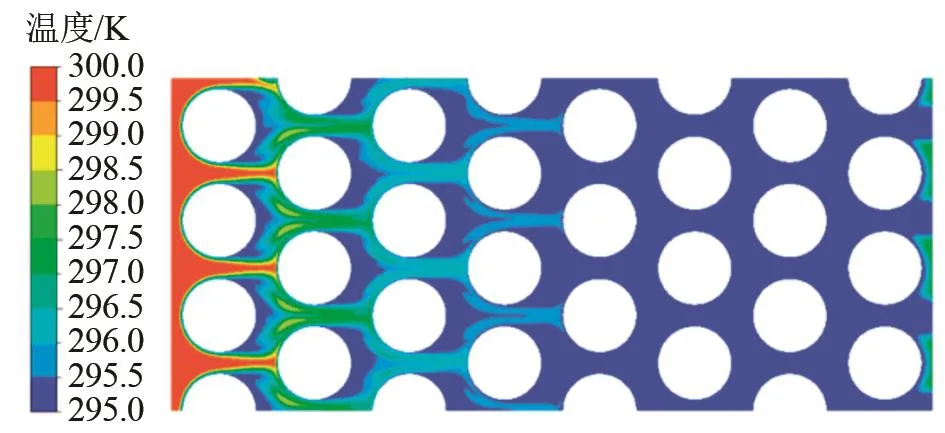
图4 高压侧换热器中部温度分布云图Fig.4 Temperature contour of mid plane in high-pressure heat exchanger

1.3 计算模型的验证

计算模型在进行优化算法前需进行网格无关性验证。高、低压侧换热器计算模型网格均为四面体网格，采用MESH生成，高压侧换热器生成网格数量为60万、100万、200万和360万，低压侧换热器生成网格数量为110万、160万、210万和440万。不同网格模型的Nu和f采用与文献[14]中相同的计算方法，并与在相同Re下该文献提出的关联式计算值Nucor、fcor进行对比，如图5所示。

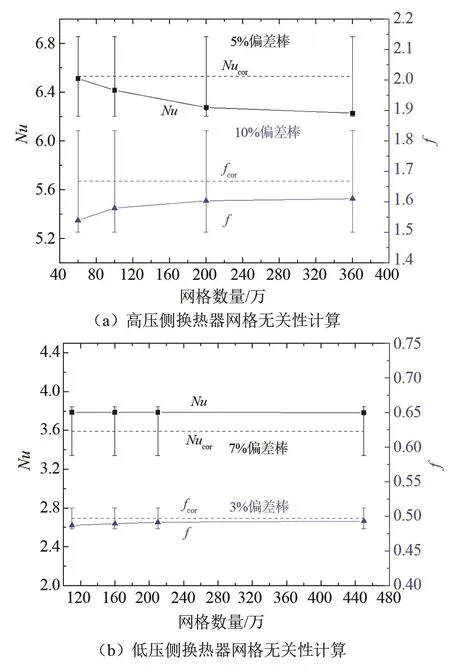
图5 高、低压侧换热器计算模型网格无关性验证Fig.5 Grid independence verification of calculation model of high and low pressure heat exchanger

由计算结果可见，随着网格数量增加，高压以及低压侧换热器模型Nu和f的变化均趋于平缓，表明当网格数量足够密集时，网格变化对计算结果影响显著减小，而过于密集的网格会导致计算速率大幅下降。高压侧换热器模型计算结果随网格数量变化更显著，应选择相对较多的网格，而低压侧换热器模型计算结果随网格数量变化不大，可选择相对较少的网格。综合考虑计算准确性以及计算速率，高压侧选择200万网格模型，低压侧选择160万网格模型，两模型的Nu和f与文献[14]中关联式的计算偏差分别为：高压侧4.0%、3.8%；低压侧5.1%、1.5%，能够满足计算精度要求。

网格无关性验证后还需对模型在各个工况下的计算精度进行验证，文献[14]高低压侧换热器性能关联式适用范围为Re≤300，因此分别对高低压侧换热器模型工况在Re=100～300进行计算验证，结果如图6所示。计算结果与关联式符合良好，高压侧换热器Nu的最大误差5.2%、平均误差2.3%，f最大误差3.5%、平均误差2.3%；低压侧换热器Nu最大误差6.1%、平均误差5.3%，f最大误差1.8%、平均误差1.5%。造成以上计算误差的原因可能是网格划分以及工质物性设置的不同。

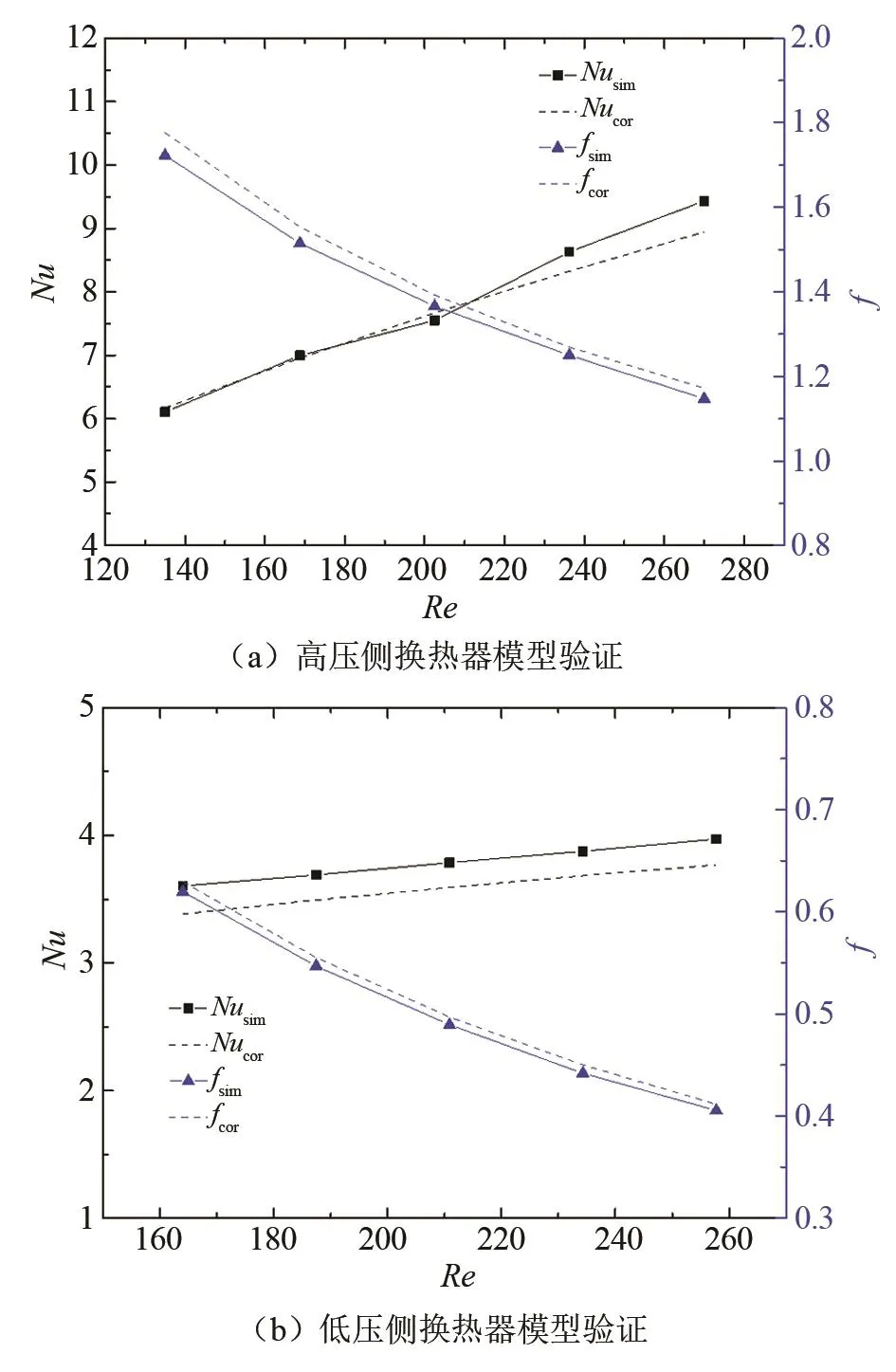
图6 高、低压换热器计算模型验证Fig.6 Calculation model verification of high and low pressure heat exchanger

2 数值计算

2.1 计算模型几何参数

高、低压侧换热器几何参数及进口条件设置如表1所列，其中柱体底部直径Dpillar以及沿流动方向相邻柱体间距Sspace为模型自变量。自变量变化范围需在一定合理范围内，否则会导致在高压工况下制冷器片键合失效，造成结构损坏。高压侧换热器柱体为交叉排布以提高换热能力，低压侧换热器柱体为垂直排布以减小流动阻力，降低蒸发腔背压从而降低制冷温度，两模型换热器柱体排列形式如图3（b）（c）。

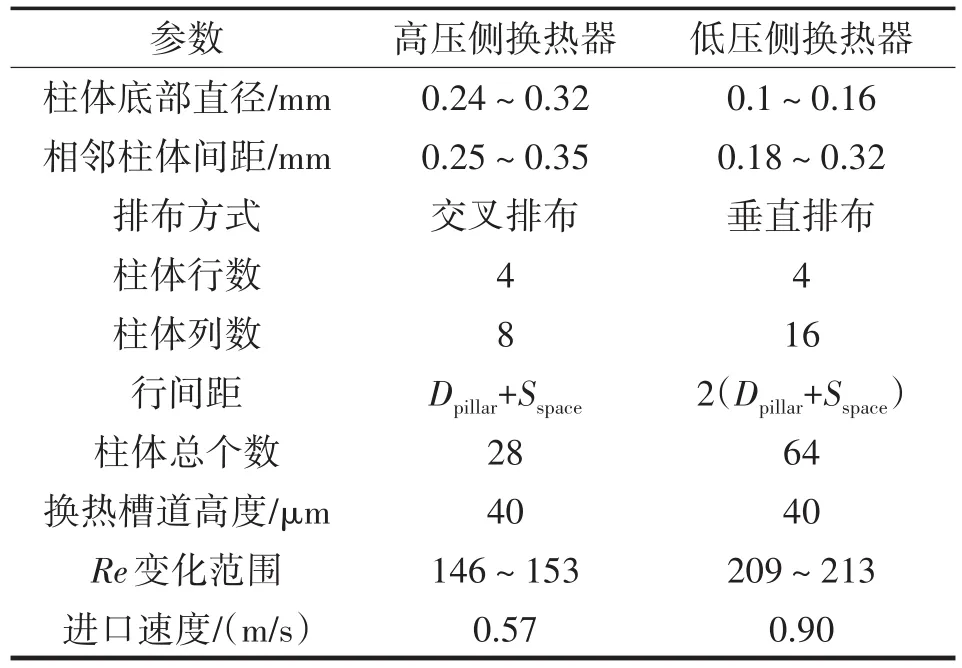
表1 高、低压侧换热器计算模型几何参数及进口条件Tab.1 Geometric parameters and inlet conditions of calculation model of high and low pressure heat exchanger

2.2 数据处理

本文采用努塞尔数Nu和摩擦因子f来表征高低压侧换热器的换热和流动性能，Nu越高换热性能越好，f越低换热器阻力越小，流动性能也越好。模型的换热性能参数Nu计算公式如下：

式中：Dh为水力直径，m；Vflow为流通体积，m3；h为换热系数，W·m-2·K-1；Q为总换热量（为计算模型中所有换热壁面的换热量总和），W；Atrans为换热面积（柱体表面积+上或下换热面），m2；Δtm为对数平均温差，K；Tin、Tout、Tw分别为进口、出口以及壁面平均温度，K。

式（8）～（10）主要计算f以及Re。

式中：Δp为模型压降，Pa；pin、pout为进口和出口平均压力，Pa；v为进口流速，m·s-1；L为换热段长度（8、16列柱体排列总长度），m；μ为流体分子黏度，Pa·s。

3 计算结果分析与讨论

3.1 响应面方法和多目标参数优化理论

在得到模型初始结构的换热和压力性能（高压侧换热器Dpillar=0.28 mm、Sspace=0.03 mm；低压侧换热器Dpillar=0.13 mm、Sspace=0.025 mm）后对高低压模型的Dpillar和Sspace进行改变，变化范围如表1所列。通过计算点设计试验计算量较小、精度高和预测性好的中心组合设计CCD（Central Composite Designs）方法[16]，从而得到计算点用于建立响应面。该方法更加强调变量边界处的取值计算，相比于传统的正交试验法所需的计算点更少、计算速率更快，更加有利于体现影响因素之间的交互作用。

响应面采用Kriging插值方法[17]，是一种通过已知点来预测未知观察点的插值方法，利用方差的变化来表达空间的变化，可以保证由空间分布得到的预测值的误差最小[18]。

利用Kriging响应面中的数据进行换热器结构多目标优化，在一定的设计参数范围内寻找同时满足Nu最大化和f最小化的换热器结构[19-21]。

3.2 响应面计算结果及分析

CCD优化算法及Kriging响应面生成的高、低压侧换热器的Nu、f关于结构变量Dpillar、Sspace的响应面如图7和图9所示，从响应面中能够大致分析出Nu、f关于结构参数的变化趋势。

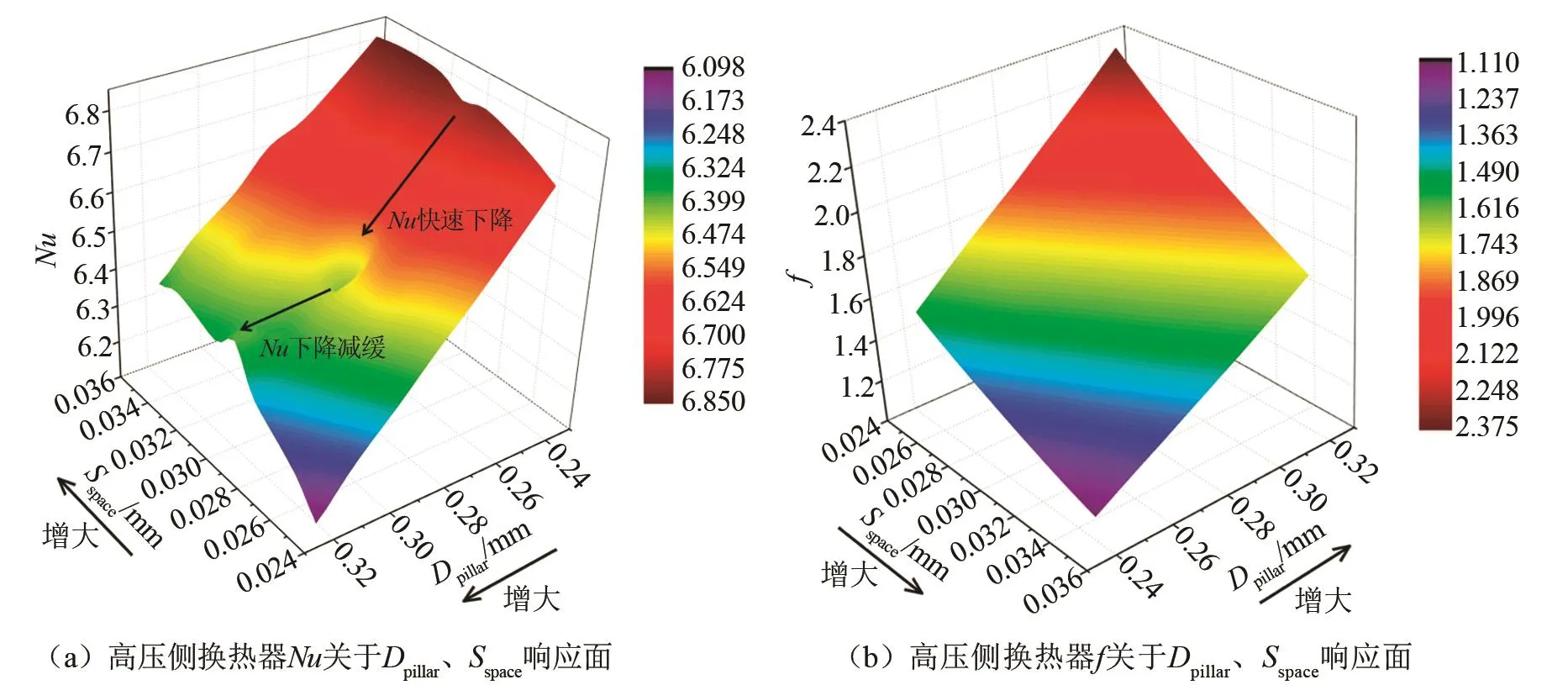
图7 高压侧换热器性能-结构响应面Fig.7 High-pressure heat exchanger performance-structure response surfaces

由图7（a）可见，高压侧换热器中Dpillar较小区域的Nu较高，在此区域较大的Sspace也能在一定范围内提高Nu。这是因为MMR换热器流道十分微小，工质流体呈层流流动，较小的Dpillar能够使得流体更易绕柱体环流流动，较大的Sspace使得层流能够更充分地发展，从而提升换热性能。值得注意的是在Sspace=0.03 mm附近Nu变化规律产生改变，此时Nu受Dpillar变化的影响更大并且在Dpillar=0.28 mm附近Nu值快速减小，图7（a）出现凹陷区域。这可能是因为Sspace在0.03 mm附近时层流流型发生较显著改变，此时Dpillar改变对换热器换热性能影响更大。在Sspace=0.03 mm时，Dpillar=0.24～0.28 mm区间Nu随Dpillar的增加减小较快，而在Dpillar=0.28～0.32 mm区间Nu随Dpillar的增加而减小的斜率较低。为了更好地对此现象进行分析，分别对Sspace=0.03 mm，Dpillar=0.24、0.26、0.28、0.30、0.32 mm五个结构进行单独研究，提取每个模型流道中部截面进口区域流体速度分布云图，如图8所示。可见随着Dpillar增加流体流速也随之增加，并且在柱体后方逐渐出现涡旋（图中方框所示），涡旋处流体滞留，在增加流体阻力的同时也对换热产生不利影响，在Dpillar=0.24～0.28 mm阶段涡旋逐渐出现并充分发展，Dpillar＞0.28 mm后涡旋无显著变化。因此Sspace=0.03 mm时Nu随Dpillar增大而变化的速率先快后慢。

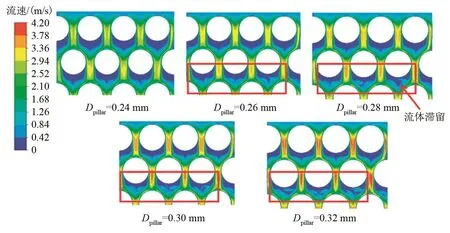
图8 高压侧换热器不同Dpillar速度分布云图Fig.8 Velocity contours of high-pressure heat exchanger with different Dpillar

由图 7（b）可见，较小的 Dpillar和 Sspace使f显著降低，当柱体更小、柱体间距更大时换热通道对流体的阻力也将减小。与之类似，在低压侧换热器中，如图9（a）（b）所示，在低压侧换热器中随着 Dpillar减小Nu显著增加，并且受Sspace影响不大。这是因为低压换热器的柱体排列行间距较大，为2倍Dpillar+Sspace，因此Sspace的改变对层流流型无显著影响。而较小的Dpillar和较大的Sspace也有利于降低换热器的摩擦因子f，并且相较于高压侧换热器，低压侧换热器中Sspace对f的影响更为显著，原因是由于低压侧换热器柱体阵列呈垂直排布，且柱体行间距大，换热器的流动阻力主要来自平行于流动方向的柱体间隙即Sspace。

图9 低压侧换热器性能-结构响应面Fig.9 Low-pressure heat exchanger performance-structure response surfaces

通过响应面计算能够得出MMR换热器换热和流动性能关于几何结构的变化规律，对换热器优化起到一定指导作用。并且根据响应面数据可同时对两个目标函数进行多目标优化。

3.3 多目标优化

换热器优化目标函数应为：努塞尔数Nu尽可能大、摩擦因子f尽可能小，这两个目标函数在某些时候存在冲突，即换热较佳的结构通常会伴有较大流动阻力。因此优化过程需首先利用响应面中数据获得Nu和f的所有非支配解的解集，即帕累托前沿（Pareto front），响应面中不存在Nu和f性能同时优于帕累托前沿中解的结构点。

自变量结构参数变化如表1所列，其中高压侧换热器Dpillar=0.28 mm、Sspace=0.03 mm以及低压侧换热器Dpillar=0.13 mm、Sspace=0.025 mm为初始结构。利用响应面得到换热器的帕累托前沿如图10所示。

由图10可见，在所有优化结构中，更高Nu的换热器结构也伴随着更高的f，为在帕累托前沿中选取更加合理的优化结构点，采用权重系数k来评价Nu和f在优化过程中的相对重要性[22]。其计算如下：

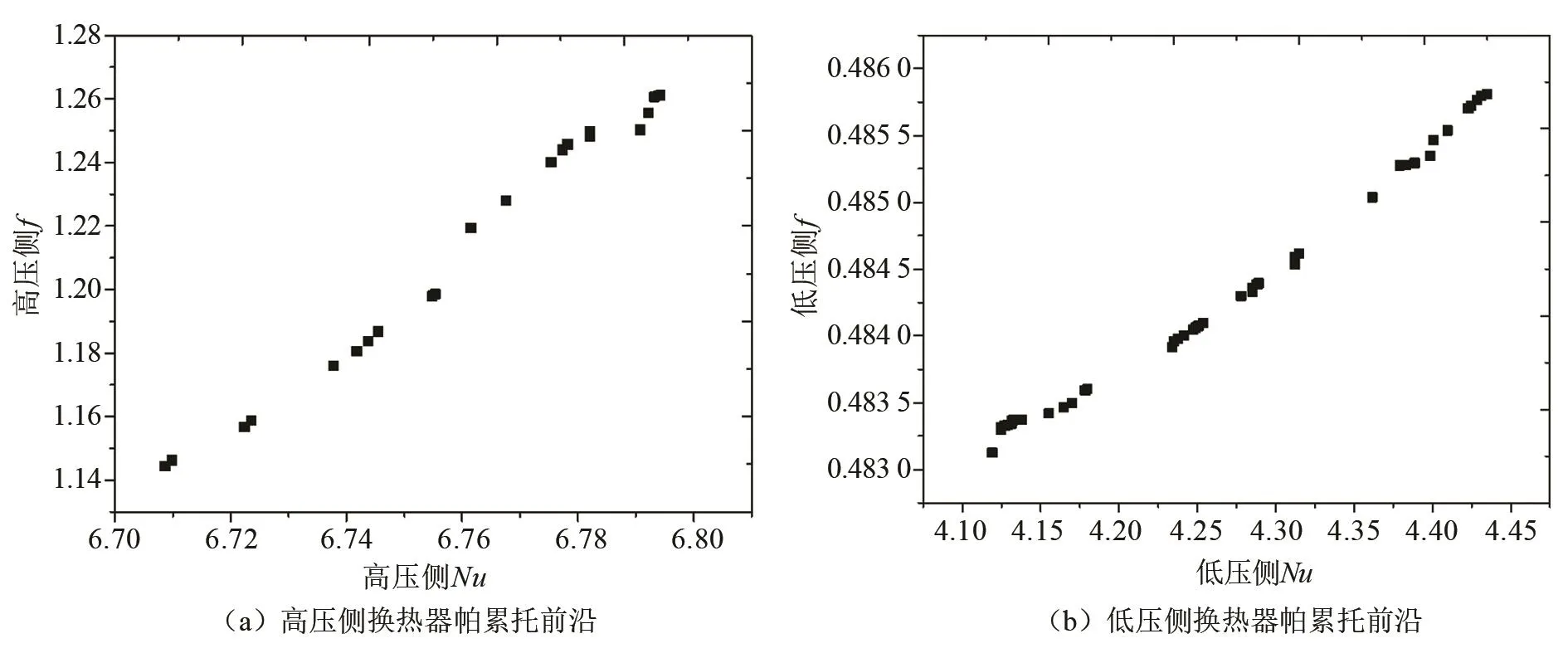
图10 计算模型优化算法帕累托前沿Fig.10 Pareto optimal fronts for calculation models

函数F（x）反映了在Nu和f的帕累托前沿变化内各备选优化点性能参数与前沿中最优性能参数Numax和fmin的偏差大小，F（x）值最小时即为Nu和f在当前权重系数下同时接近最佳性能的结构参数点。

换热器分别选取权重系数k=0.1、0.2～0.9范围内得到的优化结构参数和性能以及与原始结构对比如表2所列。

由表2可见，取不同权重系数k时，高、低压侧换热器性能较原始结构均得到了优化。根据式（11）定义，k值越高优化越倾向于强化Nu性能，反之则倾向于强化f性能。对于MMR制冷器而言，较高换热性能有利于提升降温速率，但MMR一般为非金属材料，无法通过不断提高供气压力来提升制冷性能，因此为保证制冷器有足够的节流制冷效应，流动阻力也不宜过大。根据MMR工作特性，对换热器换热和流动性能进行均衡考虑，因此选择k=0.5时的结构参数作为优化结构，并加以进一步验证和分析。

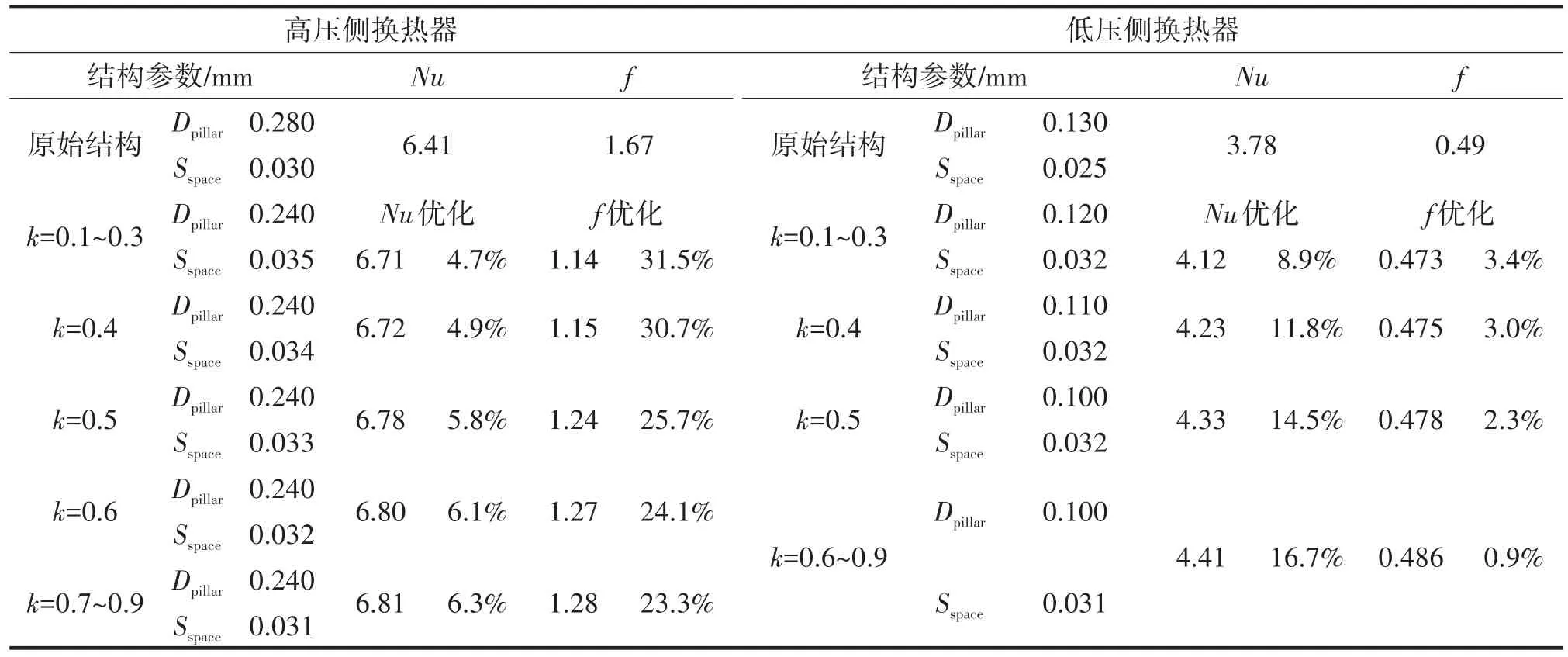
表2 换热器不同权重系数优化结果Tab.2 Optimization results of heat exchanger with different weighting factor

对k=0.5时的优化结构进行CFD重新计算，误差在1%以内，证明了多目标参数优化的准确性。本文选取高压侧换热器的最佳结构点为Dpillar=0.24 mm、Sspace=0.033 mm，较原始结构Nu提升了5.8%，f下降了25.7%。低压侧换热器最佳结构点为Dpillar=0.10 mm、Sspace=0.032 mm，较原始结构Nu提升了14.5%，f下降了2.3%。为进一步分析最佳结构与原始结构流动和换热的区别，分别选取两结构中部进口部分平面的速度和温度分布如图11、12所示。

由图11（a）可见，高压侧换热器优化结构的流体流速相对较慢，并且柱体后方的涡旋更少（图中方框所示），有利于减小流动阻力和强化换热。图11（b）进一步证明该观点，在方框所示区域优化结构的流体温度相对更低，说明具有更高换热效率。

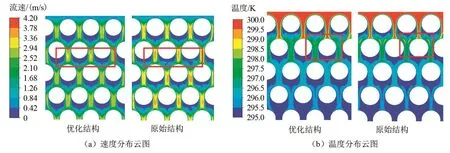
图11 高压侧换热器速度和温度分布云图Fig.11 Velocity and temperature contours of high-pressure heat exchanger

由图12可见，与高压侧换热器类似，低压侧换热器优化结构中流体流速相对较低，并且流体温度升高相同值所需的流动距离变短（图（b）中虚线所示）。

图12 低压侧换热器速度和温度分布云图Fig.12 Velocity and temperature contours of low-pressure heat exchanger

综上所述，高、低压侧换热器的优化结构较原始结构在换热和流动性能上得到提升。进一步对比优化结构与原始结构参数可得出以下结论：

对于高压侧换热器而言，较小的Dpillar能够提高换热性能，降低流动阻力；Sspace值过大时会使得换热器柱体阵列过于稀疏，从而影响换热性能。

对于低压侧换热器而言，较小的Dpillar能提升换热性能，对流动性能优化效果不明显。这是由于低压换热器的柱体阵列垂直排布以及较大行间距已经在很大程度上降低了流动阻力，进一步优化空间有限。该优化结构分别位于模型变量中Dpillar的下限以及Sspace的上限，本文未拓宽自变量取值范围做进一步计算，这是因为在实际MMR换热器中低压换热器的Dpillar不能过小，Sspace也不能过大，否则会降低换热通道表面键合强度以及使制冷器承受更大应力，在高工作压力下更易损坏。因此计算所得优化结构应该在MMR换热器结构参数合理变化范围内。

通过多目标参数优化分别得到了高、低压侧换热器在层流工况下的最佳结构点，并且优化后换热器的换热和压力性能均得到了提升。

4 结论

本文采用多目标参数优化数值模拟的方法，对结构参数影响MMR换热器的传热和流动性能进行了研究，并对换热器结构进行了优化，得到结论：

（1）参数化建模以及多目标参数优化可利用较少的计算资源实现MMR换热器的多参数变量计算以及多目标函数优化，为MMR的设计提供参考。

（2）对于高、低压侧换热器而言，较小的柱体底部直径Dpillar有利于提升换热性能及降低流动阻力。因此设计中在保证结构强度的前提下适当降低Dpillar以提升换热性能。

（3）对于高压侧换热器，适当增加柱体间距Sspace使层流更充分地发展以提高换热和压力性能，Sspace存在最佳值。对于低压侧换热器，较大的Sspace仅对换热性能存在有利影响，对压力性能影响不大。

（4）利用多目标参数优化方法得到了高、低压侧换热器在Re=150、210附近工况以及结构参数在表1所列变化范围内的流动、换热性能最佳结构，分别为：Dpillar=0.24 mm、Sspace=0.033 mm以及Dpillar=0.10 mm、Sspace=0.032 mm；Nu分别提升了 5.8%、14.5%，f分别降低了25.7%、2.3%。