非对称气体弹簧谐振系统建模与分析

水 龙，田集斌，李昊璘，王雪松

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

0 引言

往复式运动机器广泛应用于能源转换领域，如自由活塞斯特林制冷机/发电机、线性压缩机等。通常使用机械弹簧和气体弹簧为往复式运动活塞提供轴向刚度支撑，以实现活塞的稳定往复直线振荡[1-2]。其中，气体弹簧利用封闭空间内一定质量气体的可压缩性来产生作用力，通过设计附加气腔、连通管路及囊结构等，实现弹簧刚度动态调节，有效提高往复式机器运行频率[3]。

20世纪90年代，美国MTI公司在NASA支持下研发了12.5 kW自由活塞斯特林发电机SPDE和CTPC[4-5]，样机采用气体弹簧提供配气/动力活塞轴向刚度。Lewandowski等[6]以CTPC样机为研究对象，建立了包含斯特林热力学循环、机械振动和直线电机的等效质量-刚度-阻尼动态模型，分析了样机多个工况条件下从启动至全功率运行的瞬态与动态特性。在此基础上，Foster-Miller公司基于成本与时间考虑，研制了CTPC缩比样机——5 kW自由活塞斯特林发电机[7]，Raymond等[8]建立了该样机的线性与非线性分析模型。以上模型均未包含样机气体弹簧流道内气体振荡、间歇流动以及密封间隙处气体流动等动态过程。本文以兰州空间技术物理研究所研制的斯特林发电机原理样机的非对称气体弹簧谐振系统为研究对象，考虑气体弹簧连通管内气体振荡流动、平衡孔内瞬态间歇气体流动以及活塞-气缸多个间隙密封处气体流动等动态过程，通过谐振系统非线性建模与计算，对谐振系统动态特性进行分析。在此基础上，通过时频变换对谐振系统刚度特性进行分析。

1 非对称气体弹簧谐振系统

非对称气体弹簧谐振系统主要由动力活塞、配气活塞及内外缸体组成，在配气活塞与内缸体之间设计有连接管道。动力活塞与外缸体配合形成工作腔与背压腔，配气活塞与内缸体配合形成前、后气体弹簧腔，其中前气体弹簧腔通过内缸体上的连通管与附加腔保持连通。配气活塞位于平衡位置附近时，配气活塞上平衡孔与内缸体的连接管连通，实现前、后气体弹簧腔的连通；配气活塞在其他位置时，平衡孔失效，前、后气体弹簧腔隔离。非对称气体弹簧谐振系统（简称谐振系统）的基本结构如图1所示。

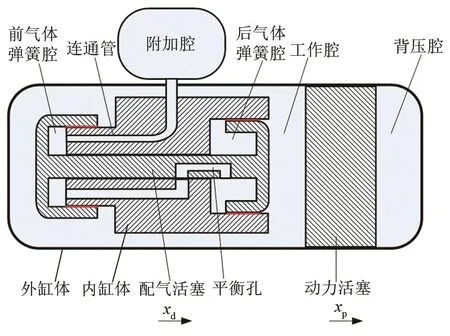
图1 非对称气体弹簧谐振系统示意图Fig.1 Schematic of the resonant system with asymmetric gas springs

在直线电机驱动下，谐振系统动力活塞受到主动力作用做简谐振动，使得工作腔内气体压力周期性变化。哑铃状配气活塞由于存在面积差受到气体压力作用[4]，在前、后气体弹簧的共同作用下做简谐振动。前气体弹簧腔与附加腔通过管路连通实现扩容，后气体弹簧腔容积较小。配气活塞在往复振荡过程中，前、后气体弹簧腔压力值存在显著差异，前、后气体弹簧的刚度也存在显著差异，具有非对称特性。

谐振系统动态特性测试实验系统如图2所示，主要由氦气源、交流电源、压力和位移传感器以及数据采集和处理单元组成，其中氦气源为谐振系统提供一定压力，谐振系统活塞位移、各个气腔内气体动态压力的变化规律分别由激光位移传感器和动态压力传感器采集并通过数据采集单元传输至示波器和计算机处理。谐振系统的设计参数如表1所列。

表1 谐振系统设计参数Tab.1 Design parameters of the reciprocating system

图2 谐振系统动态特性测试实验系统Fig.2 Experimental set-up of the resonant system with asymmetric gas springs

2 谐振系统建模

谐振系统的动子包含动力活塞和配气活塞，是一个2自由度质量-刚度-阻尼往复运动系统。动力活塞、配气活塞的往复直线运动使得气腔内气体周期性膨胀和压缩，并通过管道和密封间隙流动，气腔内气体压力的周期性变化又反作用于动子，从而影响动子的运动，即谐振系统动子的往复直线运动与气腔内气体压力变化互相耦合。

初始状态时，非对称气体弹簧谐振系统的动子均位于平衡位置，规定动力活塞的运动正方向（xd）和配气活塞的运动正方向（xp），如图1所示。

2.1 动子动力学

配气活塞运动过程中受到工作腔气体压力pw及前、后气体弹簧压力pf、pa作用，根据牛顿第二定律，得到：

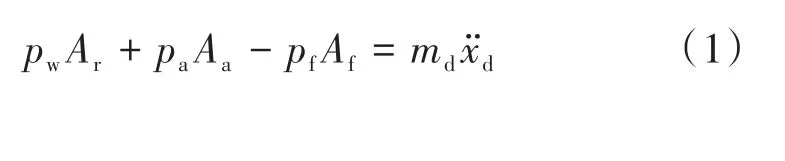
同理，动力活塞运动过程中受到工作腔、背压腔气体压力pw、pb及主动力Fe作用，可得：

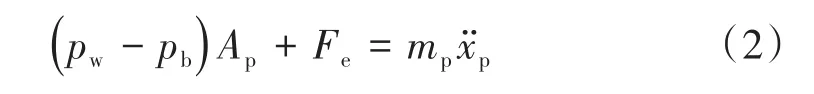
式中：̈为动力活塞加速度。

2.2 气腔气体热力学

动力活塞与配气活塞的往复直线运动使得工作腔、前后气体弹簧腔内气体周期性压缩与膨胀，将各腔内气体视为理想气体，则有：

2.3 气腔气体质量传递

谐振系统中，前气体弹簧腔与工作腔、后气体弹簧腔与工作腔之间存在密封间隙，前气体弹簧腔与附加腔通过连通管连接，前后气体弹簧腔在平衡位置附近通过管道连接。由于气腔气体压力波动的幅值和相位不同，谐振系统气腔之间存在稳定或瞬时的气体质量交换。

前气体弹簧腔与附加腔、工作腔、后气体弹簧腔之间存在气体质量交换，表示x腔与y腔之间的质量流量，因此，前气体弹簧腔的质量流量为：

同理，前气体弹簧附加腔、后气体弹簧腔及工作腔的质量流量分别为：

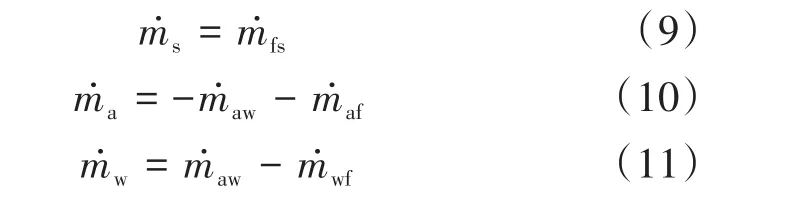
如图3为缸体与活塞配合形成的密封间隙示意图，气体通过环形密封间隙的质量流量为：

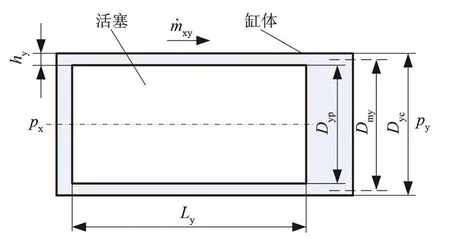
图3 密封间隙示意图Fig.3 The schematic diagram of the gap seal

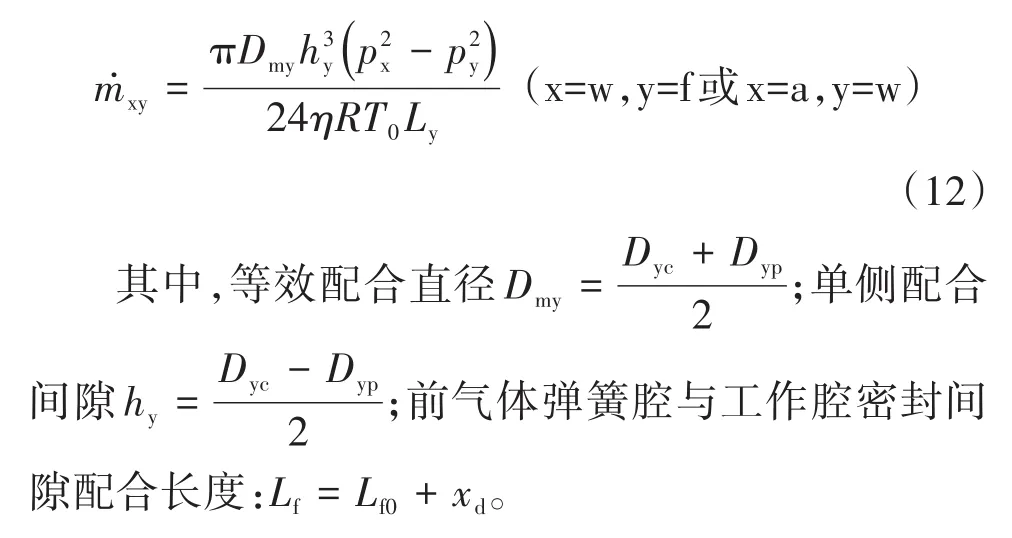
如图4为气体在两个气腔连通管道内的质量传递示意图，气体通过管道的质量流量为[9-10]：

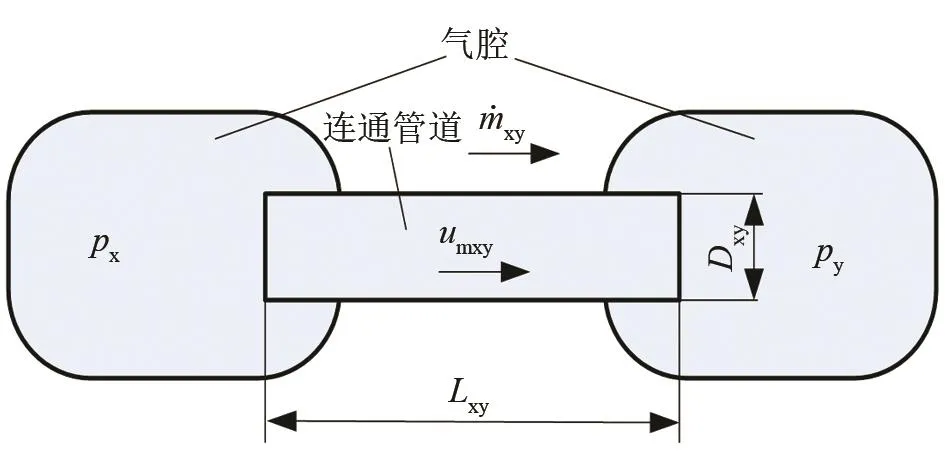
图4 气体在两个气腔连通管道的质量传递示意图Fig.4 Schematic diagram of mass transfer of gas in the connecting pipe between two gas chambers

值得注意的是，前气体弹簧腔与附加腔始终通过管道连通，而前气体弹簧腔与后气体弹簧腔仅在配气活塞位于平衡位置附近时通过平衡孔连通，前后气体弹簧腔连通面积与平衡孔面积之比随配气活塞位移的变化规律如图5所示。

3 动态特性分析

联立式（1）（2）（7）～（13），得到谐振系统动力学模型，包含 xd、xp、pf、ps、pa、pw、pb、mf、ms、ma、mw、mwf、maw、mfs和maf共15个未知变量，已知未知变量的初始值，通过数值计算可得到谐振系统的动态特性。

计算得到谐振系统动子位移、气腔气体压力、气腔质量流量、配气活塞主动力及气体弹簧力的变化规律分别如图6～9所示。

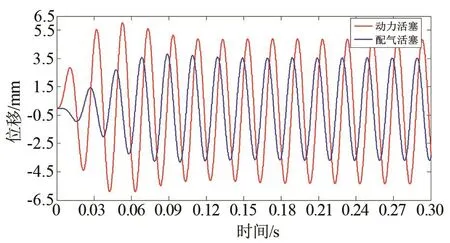
图6 动力活塞及配气活塞位移变化规律Fig.6 Variation laws of displacements of power piston and displacer

谐振系统启动后，动子振幅、气腔气体压力幅值和质量流量逐渐增大并过渡至基本保持不变，谐振系统经过瞬态达到稳定运行状态。在稳定运行阶段，谐振系统各变量随时间周期性变化，并保持稳定的幅值与相位关系，从图5、图6分别截取动子位移、气腔气体压力在0.2～0.3 s时间段内的变化过程，并与实验结果进行对比，如图10、图11所示。

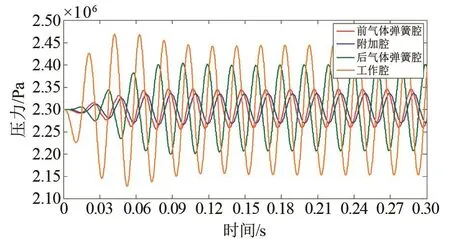
图7 气腔气体压力变化规律Fig.7 Variation laws of gas pressure

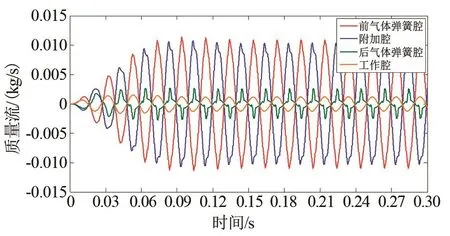
图8 气腔质量流量变化规律Fig.8 Variation laws of gas mass flow

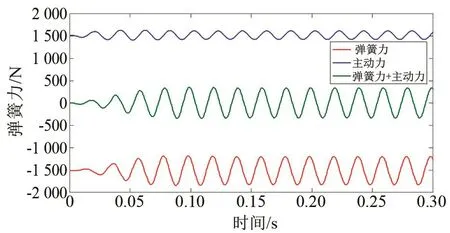
图9 配气活塞主动力及弹簧力变化规律Fig.9 Variation laws of driving force and gas spring force of displacer

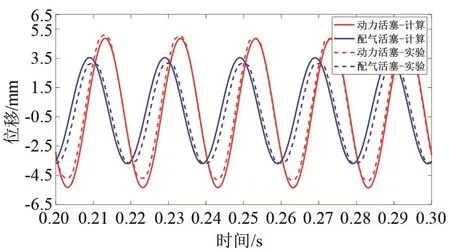
图10 动子位移变化规律对比Fig.10 Comparison of displacements of pistons

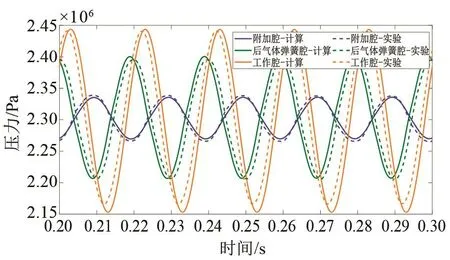
图11 气体压力变化规律对比Fig.11 Comparison of gas pressure

由计算结果和实验结果可知，在稳定运行阶段，谐振系统的动力活塞和配气活塞在主动力与气体压力共同作用下做简谐振动，振动频率均为50 Hz。动力活塞和配气活塞振幅计算值分别为5.09 mm和3.62 mm，实验测试值分别为4.86 mm和3.39 mm，两个活塞相位差约为70°。

谐振系统气腔气体压力呈近简谐变化规律，交变周期与动子运动周期一致，前气体弹簧腔通过连通管与附加腔存在稳定的周期性气体质量交换，质量流量幅值为0.01 kg/s，附加腔气体压力跟随前气体弹簧腔气体压力的交变，而压力波动幅值较小，约为0.035 MPa，与实测值接近。

由于容积存在显著差异，后气体弹簧腔气体压力波动幅值明显大于前气体弹簧腔，其压力波动幅值分别为0.095 MPa和0.046 MPa。当配气活塞位于平衡位置附近时，前后气体弹簧腔通过平衡孔连通，出现气体质量的间歇脉冲式交换。

谐振系统配气活塞受到正方向且大小均值为1 518 N的交变主动力以及负方向且大小均值为1 518 N的交变弹簧力共同作用。弹簧力幅值大于主动力幅值，两者保持稳定的相位差，弹簧力与主动力的合力为方向与大小均交变的作用力，这是配气活塞做简谐振动的根本原因。

综上所述，谐振系统动态特性的计算结果与实验结果吻合良好，验证了谐振系统建模和计算的正确性。

4 气体弹簧的刚度特性

4.1 气体弹簧的等效刚度

由谐振系统动态特性计算结果可知，前后气体弹簧腔通过密封间隙及平衡孔的质量流量较小。忽略气体弹簧腔的密封间隙泄露和平衡孔瞬时连通作用，推导气体弹簧等效刚度计算公式。前气体弹簧腔仅与附加腔存在气体质量传递，通过傅里叶变换[11]，得到前气体弹簧腔气体压力在频域的表达式为：

4.2 计算结果对比分析

根据式（18）～（21），计算得到谐振系统前、后气体弹簧的等效刚度分别为25.6 N/mm和65.9 N/mm，谐振系统等效总刚度为91.5 N/mm，分别绘制等效刚度曲线如图12、图13和图14所示。图中蓝色曲线为气体弹簧刚度曲线，红色曲线为相应的等效刚度曲线。

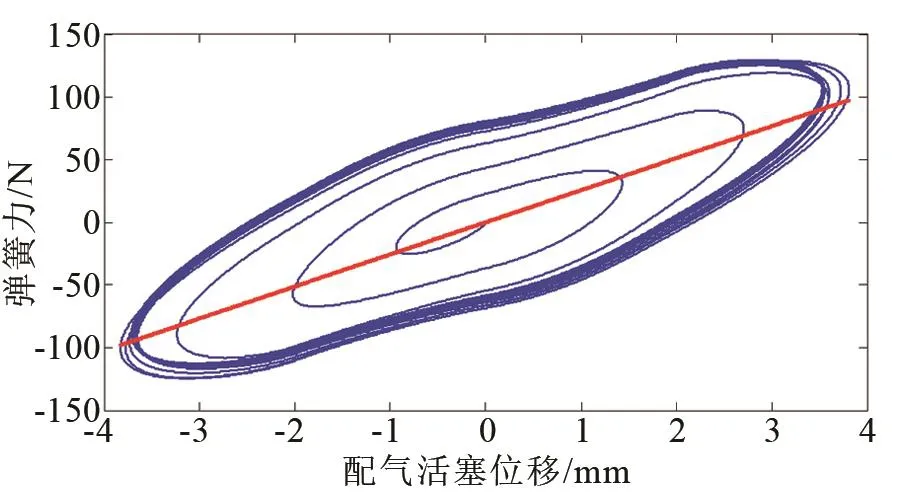
图12 前气体弹簧刚度曲线Fig.12 Stiffness curve of forward gas spring

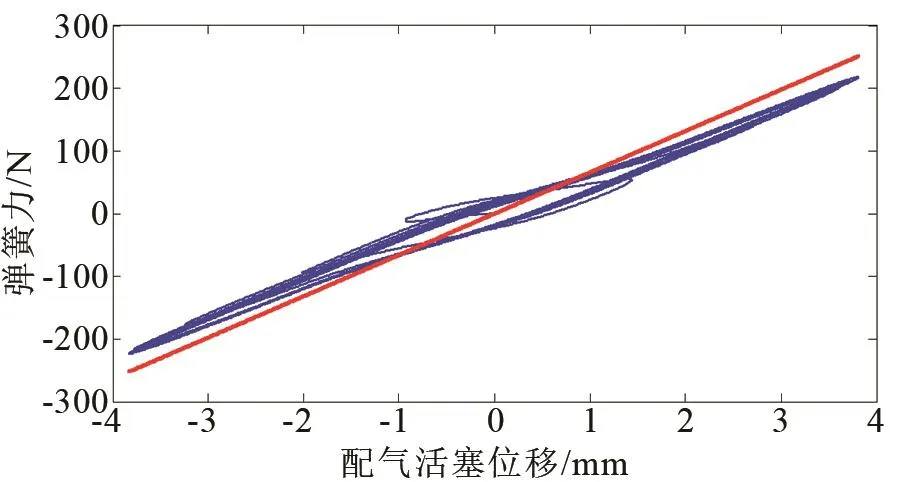
图13 后气体弹簧刚度曲线Fig.13 Stiffness curve of aft gas spring

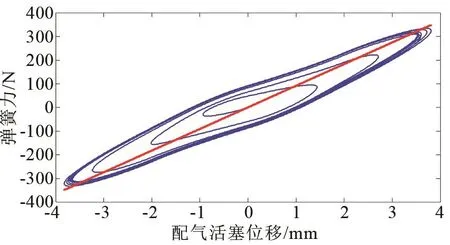
图14 谐振系统总刚度曲线Fig.14 Total stiffness curve of the resonant system

由图可知，谐振系统总刚度为其前后气体弹簧刚度叠加所得，前后气体弹簧具有非对称特性，后气体弹簧刚度曲线线性度较好。后气体弹簧刚度与等效刚度偏离的主要来源是前后气体弹簧腔的连通作用，在前后气体弹簧腔非连通段刚度与等效刚度基本一致。在前后气体弹簧腔连通段受平衡孔瞬时连通产生的气体质量传递影响，后气体弹簧刚度略小于等效刚度，后气体弹簧等效刚度占比约72%。由于前气体弹簧腔与附加腔存在稳定的周期性气体质量传递，前气体弹簧刚度曲线环绕其等效刚度近似呈“椭圆状”，非线性特征明显，前气体弹簧等效刚度占比约28%。

5 结论

针对非对称气体弹簧谐振系统的运行过程，综合考虑前气体弹簧腔与附加腔的稳定气体质量传递、前后气体弹簧腔瞬时气体质量传递以及密封间隙等因素，建立了包含动子动力学、气体热力学及气体质量传递的谐振系统动力学模型，计算得到了谐振系统动态特性，并与实验结果进行了对比分析。在此基础上，通过时频变换推导了谐振系统气体弹簧等效刚度解析计算公式，与动态刚度曲线进行了对比分析，分析结果表明：

（1）谐振系统动态特性计算结果与实验结果吻合良好，验证了谐振系统非线性建模与计算的正确性；

（2）基于动态特性计算结果绘制的气体弹簧刚度曲线与其等效刚度曲线基本一致，等效刚度能够反映气体弹簧的刚度特性；

（3）谐振系统前气体弹簧腔与附加腔存在稳定的周期性气体质量传递，前气体弹簧刚度曲线非线性特征明显，后气体弹簧刚度较大，前后气体弹簧具有非对称特性。