基于灰色神经网络的车轮多边形阶次预测

时敏栋，许牧天，朱文杰，崔 越，张 程

（上海工程技术大学 城市轨道交通学院，上海 201620）

0 引 言

车轮多边形主要遍布在车轮踏面上，是车轮不圆形式中最普遍的一种，随着城市轨道交通在各个城市的普及，车轮多边形化也变得越来越来普遍，大多数都是以一阶偏心为主，并且随着车辆的运行时长以及速度的提升，车轮磨耗也随着时间在不断地累积，多边形化亦逐渐呈现出高阶的形态。车轮多边形化会造成车轮与钢轨间的垂向作用力的不断改变，由于受力不均衡，就会直接导致车体产生垂向上的振动，降低乘坐舒适性，而且会产生高频尖锐的噪声污染。

目前，列车车轮不平顺磨耗的预测只是针对最大的不平顺值，并没有对每个采样点的不平顺点都进行预测，从而推断车轮多边形的具体发展。通用的预测手段为：人工经验、算法预测和建立动力学仿真模型。Braghin等人根据多体动力学对列车磨耗进行仿真，得到轮轨之间接触参数之后再通过Derby磨损指数理论指导对车轮磨损建立模型，精确模拟了车轮的不平顺磨损。Pascual等人通过分析运营列车中随机选取的1 000多个车轮的磨损统计数据，发现轮缘厚度越厚，其磨损速度越快。李滢等人将灰色模型和指数平滑模型相结合，实现了对车轮轮缘厚度的有效预测。

国内对车轮多边形阶次的预测研究大体上处于一个缓慢的状态中，主要的判断方法多数集中在维保人员的工作经验和建立磨耗预测模型来验证车轮未来的一个工作状态。这2种方法中，人工经验法主观性强，基本满足不了高精度数据的预测，并且目前对于车轮多边形以及形成机理的研究仍不多见，由于各种原因都会导致车轮发生多边形磨耗，相关维保部门不能及时地对相应的车轮进行镟修作业，从而导致视情维修的问题尤为突出，这就使得车轮的使用寿命大大减少，轨道交通运营与维修成本也随之增加。同时车轮多边形化严重影响列车运行安全，综合前述原因，必须对如何精确地预测出车轮多边形阶次的趋势进行研究。本文将灰色理论与BP神经网络引入车轮多边形预测领域，提出了一种基于灰色神经网络的车轮多边形阶次预测模型。该模型可根据少量的原始不平顺数据预测车轮滚动圆每个测量点磨耗的发展，再进行粗糙度的评定，推断出车轮多边形的阶次，便于制定车轮镟修计划。

1 车轮多边形阶次相关概念

列车周向不平顺是指距离轮缘内侧70 mm处车轮滚动圆半径的变化，在列车运行时，车轮踏面会和钢轨产生滑动摩擦力，并且在运行过程中不断地在加速以及制动中来回转换，这就会导致车轮半径发生周期性变化，从而形成多边形磨耗。目前，国内城市轨道交通车辆车轮主要是以偏心磨损（一阶）为主，如图1所示，但随着列车的不断运行，慢慢会出现椭圆（二阶）（见图2）、三角形（三阶）以及一些高阶的状况。

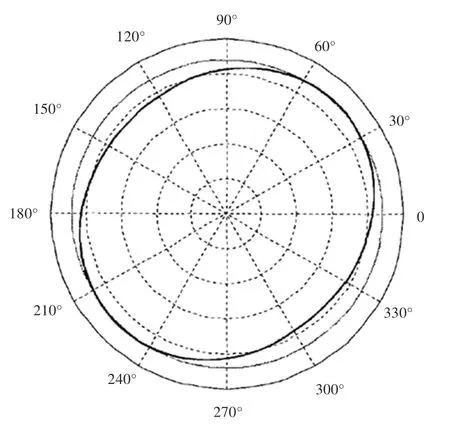
图1 一阶不圆Fig.1 The 1st order is not circular

图2 二阶不圆Fig.2 The 2nd order is not circular

本文采用激光位移传感器作为高精度测量传感器，完成对车轮滚动圆直径的数据采集，如图3所示，该设备采用的激光位移传感器重复精度达到了1μm，完全满足检测的精度要求。车轮半径采用弓高弦长测量方法来确定，其测量原理如图4所示。

图3 车轮不平顺磨耗现场采集Fig.3 On-site collection of wheel roughness wear

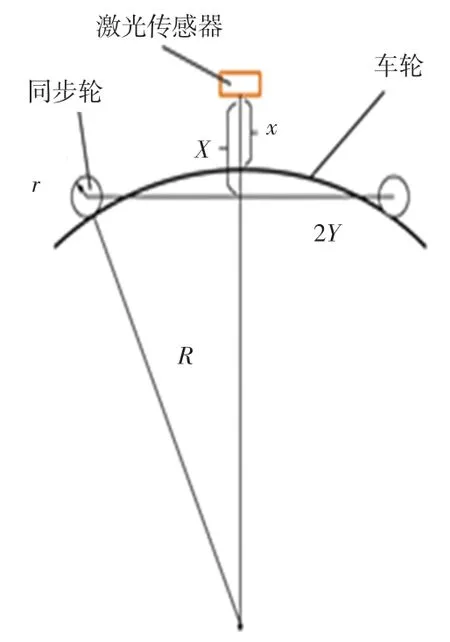
图4 车轮直径测量方法Fig.4 Measuring method of wheel diameter

由图4可知，2个同步轮半径为，2个同步轮之间弦长距离为2，激光传感器激光发射点与弦长的距离为，为激光传感器实测距车轮踏面的距离，车轮半径为，通过和标准车轮半径做比较，即可得出轮径差，其中、、的数值由机械结构设计确定，根据勾股定理有：

可得：

2 等时距GM（1，1）预测模型的建立

从系统的角度看，车轮整体的多边形阶次的发展是一个庞大的灰色系统，其中，车轮每个采样点的不平顺值是已得到确定的测量值，但影响因素“灰色信息”，不能对所有的影响因素进行定量分析。所以分析车轮多边形的发展趋势主要从时间序列角度考虑，时间的变化是影响车轮多边形阶次变化的重要因素。基于此，将灰色系统理论应用于车轮多边形阶次的预测，能够正确预测其发展趋势。对于（1，1）模型的建立，这里将给出阐释论述如下。

每个采样点的不平顺数据组含有个数据，即(1)，(2)，…，()]；对这些随机的数据进行累加操作后得到的数据组为：

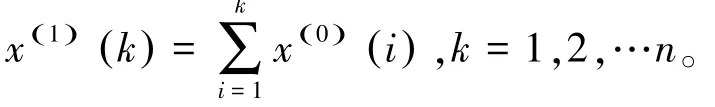
根据灰色系统理论，（1，1）模型其实是一阶微分方程模型，因而建立的灰色微分方程为：

根据最小二乘法的基本原理，可计算得到式（4）中的发展系数和灰色作用量，进行微分方程求解后，即可得到灰色微分方程的时间响应式：

3 不平顺数据预测残差修正与效果评价指标

3.1 基于BP神经网络的预测残差修正

仅通过建立单一灰色模型对每个采样点进行预测，车轮不平顺预测值存在较大的误差。BP神经网络模型在训练的时候具有高度的自学习以及非线性映射能力，而且能够解决许多模糊的、不具备线性特征、包含多种复杂因素的问题，对于无规则、样本数目巨大的残差序列，采用BP神经网络对其进行修正会更加精确快捷。对此拟展开研究分述如下。

（1）计算残差序列及归一化处理。将实测的原始车轮周向不平顺数据与灰色模型得到的预测值求差，得到残差序列：

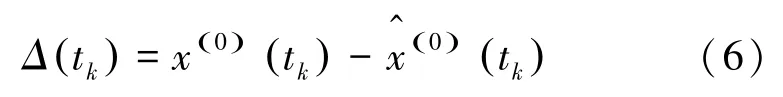
（2）确定网络训练参数。网络隐含层传递函数为函数，训练算法采用收敛速度快、运算次数少的基于Levenberg-Marquardr（LM）规则的训练函数，预测模型训练误差精度为0.001，迭代次数为1 000。

（3）BP神经网络的建立与仿真。研究中，近似使用1（为初始预测值序列个数）为网络输入（inputs），相应的预测值序列为输出（ouputs）对网络进行训练，用1（为预测次数）作为预测样本，利用函数仿真得到次的预测值序列。至此，对训练后的数据进行反归一化处理，即可得到修正过后的残差序列。

3.2 预测效果评价指标

预测效果评价指标为：使用误差来衡量单个预测值的预测效果，使用平均绝对误差（）和均方根误差（）来衡量整体预测效果，对其给出的数学定义可写为如下形式：

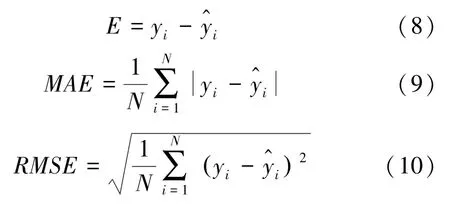
平均绝对误差是将各个预测值误差取绝对值累加之后再取其平均值，能客观反映预测模型的准确性。均方根误差将每个采样点预测值误差平方后，再对其进行求和，继而进行开方，这是衡定测量模型预测精度的常用指标。该值越小，表明预测精度越高。

4 实例分析

本文实例分析数据来自使上海地铁车辆车轮的历史周向不平顺数据序列，城市轨道交通车辆车轮直径为840 mm，所以整个车轮的周长大概在2.6 m左右，采样间隔设置为2 mm，采样周期d0.002 s，则相应的采样频率F＝1d500 Hz，采集到的数据点为1 300个，每次采集数据的时间间隔为2周，通过激光位移传感器非接触测量得到的不平顺数据如图5所示，经过滤波处理、离散傅里叶变换、再根据粗糙度定义就能得到各个阶次的粗糙度值如图6所示。从图6中可以看出，一阶偏心在该车轮的磨耗中占据主导地位，同时也存在一定的二阶椭圆化的存在，其他一些阶次的粗糙度等级数值较小，所以并没有在车轮周向上有显著的表现。

图5 车轮周向不平顺采样数据Fig.5 Sampling data of wheel circumferential irregularity

图6 车轮各阶次粗糙度等级Fig.6 Wheel roughness levels of each order

4.1 灰色神经网络的实例预测

选取上海地铁某车辆实测得到的7组历史车轮不平顺数据，对前6组数据建立的等时距灰色模型进行预测分析，每组数据时间间隔为2周。灰色模型预测数据如图7所示。由图7可见，预测2周后的车轮周向不平顺预测值与实际值存在一定偏差，得出绝对误差0.112，均方根误差0.214，可见灰色模型可以得出车轮周向不平顺数值的变化趋势，但一定存在较大的误差。为此通过计算两者的残差序列，通过一个3层BP神经网络对残差序列进行修正，隐含层采用10个节点数，采用函数为传递函数，最终预测结果如图8所示。由图8可见预测数据与实际测量数据基本上重合，经过计算，可得绝对误差0.04，均方根误差0.101，2个数值都有大幅度的缩小，说明在预测精度层面来说，灰色神经网络模型要远远好于灰色模型，更能反映出车轮整体的不平顺状态。

图7 灰色模型预测数据Fig.7 Grey models predicted data

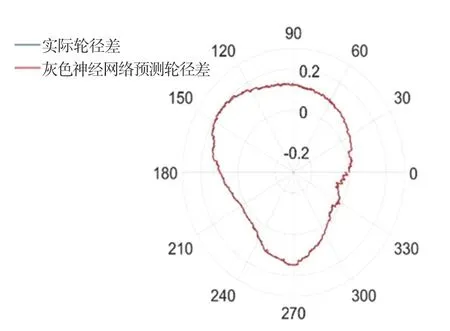
图8 极坐标下灰色神经网络模型预测Fig.8 Grey neural network model prediction in polar coordinates

4.2 预测数据的多边形阶次提取

每个波段的多边形阶次就是一段特定频率完整的谐波，研究中把采集到的不平顺数据在频域上进行分析，当某一段频率在频域中的能量最大，则说明这段频率代表的多边形阶次在车轮踏面上表现得更加显著或者说是处于主导地位。假设测量的数据长度为1时，则1～20阶多边形对应的阶次频率就分别为1 Hz，2 Hz，…，19 Hz，20 Hz。基于该理论，为了得到车轮各个阶次的多边形粗糙度等级，首先得对预测数据进行低通滤波处理，接着利用FFT对滤波后的不平顺值进行频域中的分析，再通过粗糙度等级的定义对各个阶次的粗糙度进行计算，10μm粗糙度的有效幅值对应20 dB的粗糙度等级。通过灰色神经网络利用已有的7组数据来建立预测模型，得出2周之后的车轮不平顺数据，经过上述处理后最终的结果如图9所示。由图9的结果分析得知，虽然该车轮的一阶偏心还是最显著，但二、三、四、五阶多边形的粗糙度等级也在不停增大，高阶多边形数值虽然也有所增大，研究同时发现粗糙度等级却并未显得非常突出，可见随着列车运行时间越久，车轮多边形会从一开始的一阶偏心向更高的阶次演变，最后的趋势就是往高阶多边形化发展。

图9 车轮各阶次粗糙度等级Fig.9 Wheel roughness levels of each order

5 结束语

本文根据历史车轮周向不平顺数据建立了一种基于灰色神经网络的车轮多边形阶次组合预测模型，主要利用等时距（1，1）对车轮每个采样点数据建立不平顺预测模型，再通过BP神经网络对每个采样点的预测数据的残差序列进行修正，解决车轮周向不平顺发展趋势中不确定性问题，最后对预测数据进行离散傅里叶变换以及低通滤波处理，根据粗糙度的定义得到车轮各个阶次的粗糙度等级，通过各个阶次粗糙度的数值大小来判断车轮多边形阶次的发展趋势。并且以上海地铁某车辆实测数据展开了灰色神经网络模型的实例预测分析，结果显示，这种组合预测模型预测效果的平均绝对误差与均方根较单一的灰色预测模型均有所降低，模型预测精度得到提高，证明了模型的有效性，并且可以从最后的各个阶次的粗糙度等级得出，随着列车运行时间的不断增加，车轮多边形也会不断向着高阶多边形化发展，可为工务部门制定车轮镟修策略提供重要指导意义。