基于降维算法从少量测量数据中重构温度场
罗 芸,钱 进,王一桂,朱道兴
(1贵州大学 电气工程学院,贵阳 550025;2中国电建集团贵州工程有限公司,贵阳 550025)
0 引 言
温度分布信息对锅炉、大气层、海洋等的监测都非常重要,其获取方法大概可以分为2种:计算方法和测量方法。在实际应用中,2种方法都有其局限性。计算方法是将数学问题离散化形式表示,但由于计算方法运算过程复杂且对计算资源要求较高,温度信息再现实时性差。测量方法受测量环境、被测物结构、测量设备安装以及工程造价等因素的影响,难以获得全面温度分布信息。
为了对适合工业现场温度分布进行快速、准确的重建,将降维算法引入温度分布重建,综合计算方法和测量方法的优点,由计算方法提供温度分布重建的样本数据集,测量方法得到少量温度传感器数据,使用数据降维算法提取样本数据集中温度分布特征,结合有限温度测量数据对温度分布实现实时重建。
利用本征正交分解(POD)降维方法进行温度分布重建以及分析,获得良好的效果,也是近些年来的研究热点。POD算法是数据驱动的维度降低算法,从大量的已知数据中提取元数据的主要特征,得到原数据的低维表达。Woojin等人采用本征正交分解方法提取低维基向量,重构了500 MW切向燃烧煤粉锅炉温度场,重构效果良好。在POD方法的基础上Sirovich等人首次提出了Gappy POD方法,该方法利用POD基结合部分测量数据重建缺失数据进行补全重构。与常用的基于POD的降维方法相比,Gappy POD的显著优点之一是其系数矢量是根据部分测量数据求解的,不需要了解测量对象物理过程的详细信息。Lei等人基于Gappy POD方法,提出数值模拟信息和测量信息相结合,从局部测量数据中重建稳定温度场,通过数值仿真验证了其可行性和有效性。陈敏鑫等人、及孙单勋提出了一种将CFD信息融合至Gappy POD算法中实现了对物理场的实时重建方法,该方法重建范围大,准确性高,为未来物理场预测重建提供了一种新的思路。
综上所述,提出基于Gappy POD算法,结合部分测量数据对温度场进行准确重建,具体重建流程如图1所示,并分析研究Gappy POD算法进行重建时,POD基个数、传感器数量和测量位置等因素对温度场重建的影响。

图1 重建流程Fig.1 Reconstruction process
1 本征正交分解方法
1.1 标准POD方法
标准POD方法主要思想是将原始温度场分解为基函数(POD基)和基系数的线性组合。应用POD算法,原始温度场组成的快照矩阵的大部分信息由少数POD基近似表示,进而实现了降维。
将多组温度场数据构成快照矩阵合集(x,t)(1,),是空间坐标,是温度场标量编号。其样本矩阵形式可表示为:

计算快照矩阵各个节点的平均值,即:
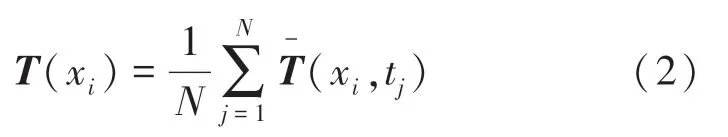
由此得到温度场的脉动量矩阵,即:


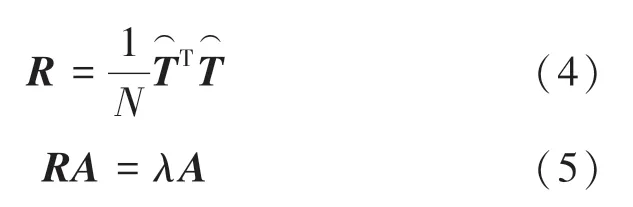
其中,为特征值,为特征向量。
通过式(6)、式(7)可以计算各阶POD基Φ()和其对应的模态系数a(),具体公式如下:

POD基表示捕获温度场的主要特征,前个POD模态所捕获的能量占全阶模态的能量为:

快照矩阵中任意温度场可以由温度场的平均值和一组基模态和线性组合来重构,即:

1.2 Gappy POD方法

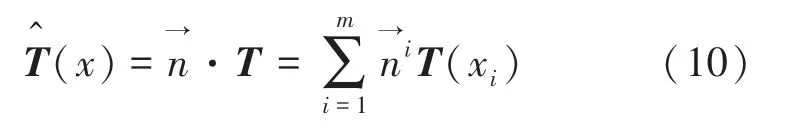






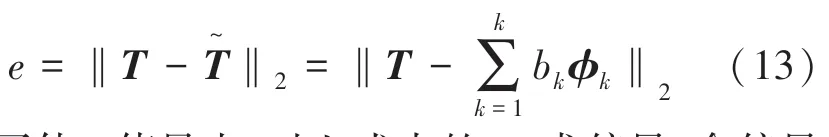
为了使值最小,对上式中的b求偏导,令偏导等于0得到误差最小值。研究推得的数学公式如下:

整理得:

进一步地,可以计算出:


为了后文的论述,定义均方根误差为重建误差:
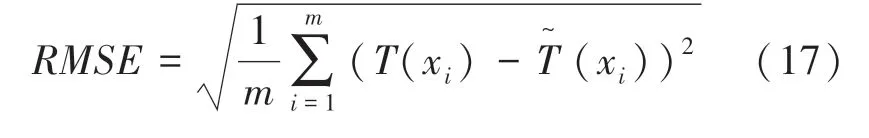
2 温度场重建仿真研究
2.1 二维温度场模型仿真
为了对待测对象进行二维温度场仿真研究,采用双峰偏斜温度场模型,运用Matlab软件进行仿真实验。
双峰偏斜数学模型:
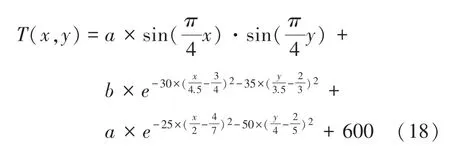
其中,(,)表示双峰偏置温度分布模型坐标点(,)处温度值(K);表示横坐标(m);表示纵坐标(m);、表示边界条件。
使用式(18)在计算区域内计算温度值,计算区域为4×4 m,采样步长为0.1 m,采集1 681个温度值,形成温度分布数据。计算不同边界条件下的温度分布数据,构建样本数据集以及测试集。设定双峰偏斜温度分布模型样本数据集以及测试集边界条件见表1、表2。

表1 样本数据集边界条件Tab.1 Boundary conditions of sample data sets

表2 测试数据集边界条件Tab.2 Boundary conditions of test data sets
根据表1、表2给出的边界条件,共有30组样本数据和5组测试数据,应用公式(15),计算温度分布数据,采样形成维数为1 681×30的样本数据集和维数为1 681×5的测试数据集。
2.2 温度场重建结果
在本节中,使用Gappy POD方法结合部分温度测量数据重建温度场。将样本数据集进行特征分解,按照公式(8)确定POD基的个数,构成转化矩阵,选择几个坐标点作为实际温度测点,坐标点的温度数据作为温度测量值,结合转化矩阵对测试数据集进行温度场重建。
首先对30个不同工况的样本数据集进行POD分析,得到用于重构温度场的POD基。不同POD基所占能量曲线和前两阶POD模态分别如图2、图3所示。从图中可以看出前两阶POD模态所占能量几乎是总能量的100%,这意味着高维数据可以用2个空间模态来准确表达,高维数据可以得到显著压缩。

图2 各阶POD基所占能量Fig.2 The energy of each order POD base

图3 前两阶POD模态Fig.3 The first two order POD
其次,对表2中的5组测试工况选择前两阶POD模态、10个温度测点和相同测点位置进行温度分布重建。重建结果如图4所示,图4(a)~(e)展示了测试工况原始温度场,图4(f)~(j)给出了重建温度场结果。按照公式(17)计算重建误差如图5所示。

图5 测试工况重建误差Fig.5 Test condition reconstruction errors
由图4可以看出,重建温度分布与原始温度分布大致保持一致,重建效果良好。

图4 重建结果Fig.4 Reconstruction results
图5 中,样本工况范围内的测试工况1~3的重建误差小于在样本范围外的测试工况4~5的重建误差,但其温度分布重建效果同样良好,全部测试工况重建误差均在1×10之下;测试工况4离样本工况范围近,测试工况5离样本工况范围远,测试工况5的重建误差大于测试工况4的重建误差。因此结合Gappy POD和部分测量数据的温度分布重建算法有着良好的适用性和准确性。
3 温度场重建结果误差分析
针对温度场的重建,使用控制变量法来分析POD基个数、传感器数量(测点数量)、传感器放置位置(测点位置)等因素对重建结果造成的影响。为了消除实验带来的随机误差,所有结果均进行了多次,做图数据为多次实验的平均值。
3.1 POD基数量对重建结果的影响
图6中展示了测试工况1的重建误差随着POD基数量的变化情况。利用10、50和70个实际测量数据,在固定的测量数据情况下,随机选取不同位置的测点进行温度重建计算,做图数据为多次计算的平均值,消除测点位置对结果产生的影响。从图6中可以看出,使用前两阶POD基进行重构,比使用前一阶POD基进行重构,重构误差大大减小,重构误差随着POD基数量的增加,先减小、而后趋于稳定。3种不同的测点数据下,重建误差随POD基数量的变化保持相同的趋势。

图6 利用10、50和70个测量数据,重建误差随POD基数量变化曲线Fig.6 The reconstruction errors curve with the number of POD bases by using 10,50 and 70 measurements
3.2 测点位置对重建结果的影响
图7为3和5个传感器在随机位置点的重构误差。
从图7中可以看出,由于测量数据的测点位置是随机的,即使同样数量的测点数据,测点位置不同,重建误差变化较大。

图7 3和5个传感器数量在随机位置点下的重构误差Fig.7 Reconstruction errors of 3 and 5 sensors at random position points
图8为利用2个POD基在不同传感器数量和不同随机位置下重构的误差,选取不同数量的测量数据,随机选择测点位置,进行5组实验,得到5组计算结果。由图8可以看出,不同随机位置测点的重建误差均是随传感器测量数据数量的增加由降低到趋于稳定,但测点位置不同,其重建误差也不相同。

图8 不同传感器数量和不同随机位置的重建误差Fig.8 Reconstruction errors of different random positions with different number of sensors
由此可见传感器的放置位置十分重要,不同的放置位置对其在温度分布重建算法中影响程度也不同。
3.3 测点数量对重建结果的影响
在传统的温度预测和重构中,预测和重构结果准确度高需要大量的传感器测量数据做支撑,然而,大量传感器使用却需要大量资金、人力和物力投入。因此,尽量少的传感器数量使用也是衡量预测重构模型的标准之一。由上文可知测点位置对重建结果的影响,为消除此影响,对此进行多次计算取平均值。
利用一阶、二阶和三阶POD基进行重建,重构误差如图9所示。由图9可以看出,一阶POD基重建误差随传感器数量增加虽呈下降趋势,但过程跌宕起伏;二阶和三阶POD基重建误差随传感器数量增加而减少、再趋于稳定。一阶与二、三阶趋势不相同,这是因为一阶POD基所占能量较低,对数据反应能力较弱,这与前文中提出的结论是一致的。

图9 不同POD基在不同传感器下的重构误差Fig.9 Reconstruction errors under different sensors with different POD bases
由图8和图9可知,重建误差均在测点数量为5后趋于稳定,由此可知传感器最佳数量为5个。
4 结束语
(1)针对有限的已知测量数据的温度场重构,本文结合Gappy POD方法,利用少量POD基能够快速准确地重构温度场,为了验证算法的可行性和适用性,重建5组测试工况,重建误差均在精度要求范围内,对于其边界条件不在快照矩阵范围内的测试工况4、5的重建,仍有令人满意的重建结果。
(2)重构误差随POD基数量的增加先减少、而后趋于稳定,少量的POD基就能重构温度场,对后续低阶模型有一定指导意义。
(3)同样数量的传感器,放置位置不同,重建误差变化较大,由此可见测点位置所携带信息重要程度在重建算法中也各有不同,因此测点位置的优化布置尤为重要,后期会对最佳测点位置方式进行研究。
(4)重建误差随传感器数量的增加先减少、再趋于稳定,根据成本和计算准确性考虑,传感器布置最佳数量为5个,显著地减少测量传感器的数量,可降低温度分布测量的复杂性与测量成本。

