一种基于改进型Chameleon算法的宿舍分配方法

顾唐杰，秦 波，蒋小菲

（贵州大学 大数据与信息工程学院，贵阳 550025）

0 引 言

当代年轻人拥有多样化的性格，这也将导致部分学生在人际交往过程中会出现各种各样的问题，在这些问题中室友往往担任着非常重要的角色。良好的宿舍氛围不但促进了学习进步，也提高了学生的生活质量，为大学生心理健康起到正面积极作用。然而近几年关于同寝室犯罪的报道却已开始映入眼帘，抛开极端情况不谈，在普通宿舍中也不时会出现因室友性格不同而导致的宿舍“小团体”现象或校园霸凌问题。根据新华网一项针对大学生舍友关系的调查显示，42.28%的学生与舍友曾经发生矛盾；与舍友发生矛盾时，仅有47.81%的学生会选择“积极沟通”。显然对于部分学生的矛盾很难通过教育、引导途径化解。

在此背景下智能宿舍分配方法孕育而生，2016年，上海大学的高校公寓“私人定制”计划采用了网上选室友计划。而在国外，学生也可以通过网络选择室友。为进一步满足学生宿舍需求，本文通过调研学生共性，对学生中性格习性相近或互补的学生进行聚类，并对Chameleon算法做出改进得到一种全新算法。

Chameleon算法是由CURE和ROCK算法演变而来，兼顾了接近度和内部互联度，在二维数据的聚类中取得了非常好的效果。目前，Chameleon算法也在不断的发展中出现过比较典型的改进。例如龙真真等人提出了M-Chameleon算法，改进后不但减少了聚类过程中所需的参数，并能更加客观地反映聚类情况。宫峰勋等人的《基于DPC算法与模块密度的改进Chameleon算法》中，在传统算法的基础上于图划分阶段利用密度峰值算法使稀疏图的划分更为准确，并在后续聚类过程中采用集群数据点相似性的函数获得最终的聚类结果。

结合以上算法优点，本文通过对Chameleon算法改进得到KSNN-Chameleon算法。KSNNChameleon算法在针对学生宿舍分配问题时，能够通过学生之间共性的差异进行智能宿舍分配。在查阅相关资料和社会调查后，本文按照学生的兴趣爱好、月生活水平、学习习惯、作息时间、嗜好等，对每一位学生的特点进行划分并通过Matlab软件进行分析推测出适合每一位学生的室友。

1 算法理论分析

本算法是在Chameleon算法的基础上进行改进和提炼的新型KSNN-Chameleon算法。本节将介绍KSNN-Chameleon算法的理论依据，以及对传统算法中各个阶段的改进。

1.1 Chameleon算法

聚类分析中的层次分析法可以笼统地分为：由整体分裂的方法和由多点凝聚的方法。这取决于层次分解当中分解的顺序，而Chameleon算法采用动态建模的方式进行聚类。Chameleon算法流程如图1所示。由图1可知，首先需要对数据项进行稀疏化，然后通过相关的图划分算法对稀疏图进行划分，从而形成多个相对连接性较高的初始子簇。最后使用凝聚层次聚类技术，重复合并相似性高的簇。即Chameleon算法是先对整体进行分裂，又采用凝聚的方法进行二次聚类的聚类算法。Chameleon算法最大的优点在于，既考虑了每个簇的相对互连度( C，C)，又考虑到簇的相对邻近度( C，C)，通过二者相结合的相似度函数计算数据点之间的距离。

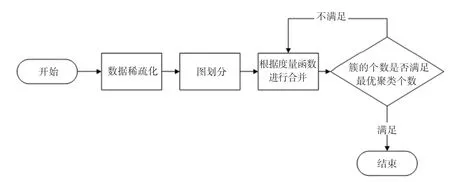
图1 Chameleon算法流程Fig.1 Chameleon algorithm flow chart

定义1 相对互连度( C，C)2个簇C和C之间的绝对互连度关于C和C的内部互连度的规范化，即：

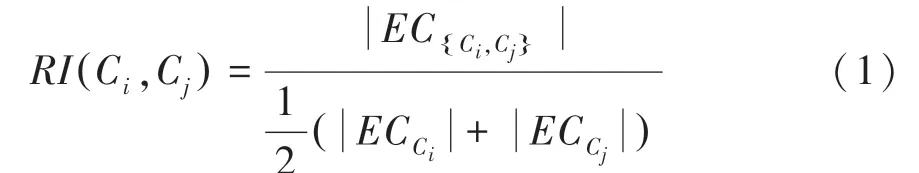
定义2 相对邻近度( C，C)2个簇C和C之间的绝对接近度关于C和C的内部接近度的规范化，公式如下：

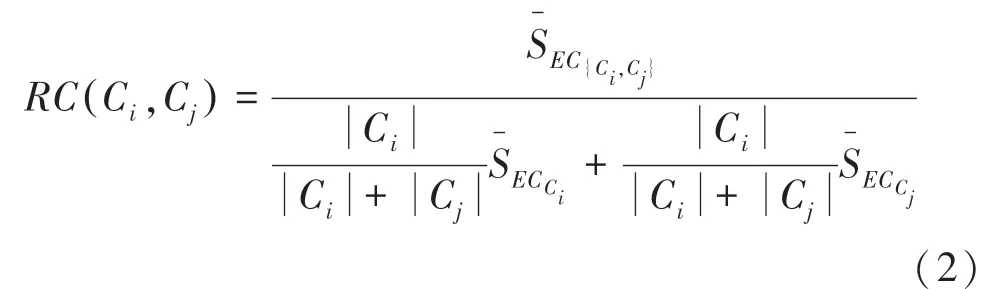
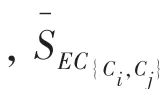
相对互连度和相对互连度的乘积，即：

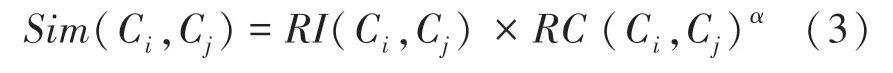
其中，是指定参数，设定两值的权重。例如，当1，代表2个度量标准权重相同；如果1，则Chameleon更偏重于相对接近度；反之，当1时，则偏重相对近邻度。

1.2 改进稀疏化

Chameleon算法的第一个阶段（稀疏化过程）是通过K最近邻法求出数据点的K最近邻图的过程，得到的K近邻图被称为数据集的稀疏图。此方法计算数据点关系时采用的是欧式距离法，对于偏重于距离分析的Q型聚类问题，这种方式可以有效地将数据点进行分类。然而，当遇到利用数据相关程度进行聚类的R型聚类问题时，这种聚类方法的适用性就会有所下降。因此，为了更好地利用稀疏图进行图划分，KSNN-Chameleon算法在稀疏化得到K近邻图后，将K近邻图转换为加权近邻图。

1.2.1 利用KD树减少总体聚类时间

由于本算法需要对K近邻图进行转换，聚类时间也随之增加。KSNN-Chameleon在K近邻算法的基础上利用KD-tree原理对其进行改进，大大减少了聚类所需要的时间。

根据目标点的距离度量，在输入数据集中找出与最近的个点，涵盖着个点的领域，记为N（），若N（）中某一个簇类C的出现的次数最多，则判定目标点也属于C。

是一种对K维空间中的实例点进行存储以便对树形树状结构进行快速检索。是空间二分树的一种特殊情况。

1.2.2 加权近邻图

传统K近邻图仅仅只能体现出数据点之间的位置关系和距离关系，而面对R型聚类问题时，利用欧式距离描述数据点之间的位置关系是不太准确的。为更好地解决R型聚类中，稀疏图依赖距离的问题，本文将得到的稀疏图，通过近邻度权重的方式进行改良从而得到加权近邻图。利用加权近邻图进行图划分可以更有效地避免R型聚类问题中依赖距离因素的问题。

公式如下：

其中，是分簇个数，a是点和被分为同一个簇的次数。若（，）≥05，则和为彼此的近邻点。

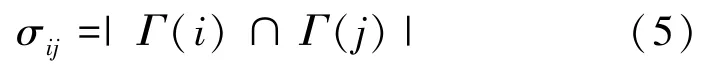
交集个数表明，若两者越相似，则所拥有的共同近邻点就越多，权重越大。根据以上定义得到算法1，用以得到加权近邻图。

含个数据点的数据集｛，，…，x｝

加权近邻图

1：Int中数据点的个数

2：For（1；；）

3： For（1；；）

4：（，）（，）；

//计算两点近邻度

5： End for

6：End for

7：If（（，）05）then

8： do∈（），∈（）

9：End if

10：If（∈（）‖∈（））then

11：σ＝Γ（）∩（）

计算两点间的权值

12：End If

13：__（，，σ）

1.3 改进图划分

Chameleon算法的第二阶段在得到稀疏图后会直接采用hMetis划分算法对获得的稀疏矩阵进行图划分。hMetis是一种多层次的分割方法，在处理粗糙图形信息上具有良好的效果并且聚类的时间更短。但考虑到hMetis算法不开放源代码，并且hMetis算法是一种采用最小可能性切割边缘进行图划分的方法，有时会产生距离很远却聚为一类的问题，所以在处理一些信息时达不到理想的聚类效果。为了更好地实现图划分，KSNN-Chameleon算法采用flood-fill法结合递归二分法，代替原有的hMetis算法，对得到的加权近邻图进行图划分。详情见算法2。

raph

多连接子簇

1：whiledo

2： For∈（）do

3： Ifisthen

4：_（）

综合能源系统是能源互联网的物理载体,主要着眼于解决能源系统自身面临的问题和发展需求,其研究不过分强调何种能源占主导地位。

//创建新空间存放数据点

5：__

（，，）

6： End If

7： End for

8：End while

9：__（，，）

10：（，）标记簇中的点

11：Forin（）do

12： Ifisthen

13：__（，，

）建立多连接簇

14： End If

15：End for

给区域内某一个点上色，并对所有相邻的点依次涂上的颜色，不断填充此区域，直到区域内的所有点都附上颜色。

1.4 合并阶段

本算法在Chameleon聚类的第三个阶段合并时主要针对2个部分进行改良。一方面传统算法在针对二维数据集时，采用的相似性度量函数可以有效地将图划分后的各个数据簇进行分析和合并，但是在面对三维以上的数据集时，其聚类效果会随着维度的升高而下降。为了在高维R型聚类问题中，得到更加精准的聚类簇，KSNN-Chameleon算法采用共享最近邻相似度的方法进行改进，从而避免高维情况下的维数灾难。另一方面，传统算法中需要反复计算目标数据集的最优聚类个数，这一过程消耗大量的时间，而KSNN-Chameleon算法采用第一截断法的方式，对该过程进行简化，可得到数据集聚类的最佳簇数。

1.4.1 共享最近邻相似度

为了解决高维度问题，本文引入共享最近邻相似度代替传统相似性度量，由于共享最近邻相似性度量在空间中主要反映的是点的局部结构，因此对空间的维度并不敏感，所以可作为一种相对合适的度量方法。共享最近邻相似度可以理解为：对于2个不同的数据点而言，如果彼此的相似点中，存在着大量重合的部分，那么即可判定这2个数据点也相似。如图2所示，点和都有8个最近邻居，其中有4个点是和都共有的，称为共享邻居，所以，点和点之间的最近邻相似度为4。

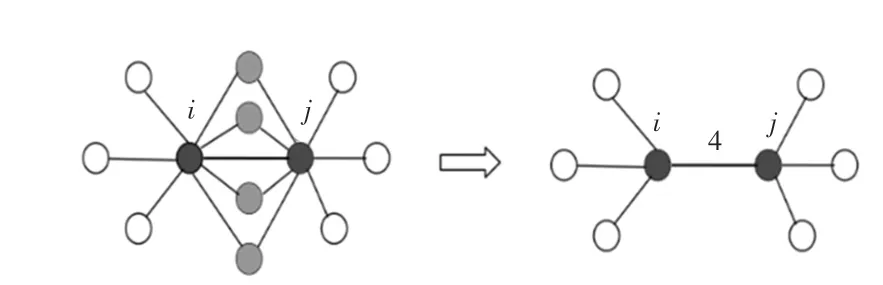
图2 共享邻居展示图Fig.2 Shared nearest neighbour diagram

在数据集中存在任意2点和，将点的个近邻集合设为（），同理将的集合设为（），则点和的的公共邻居集，定义如下：

对于数据集的任意数据点和，其共享最近邻相似度可定义为：

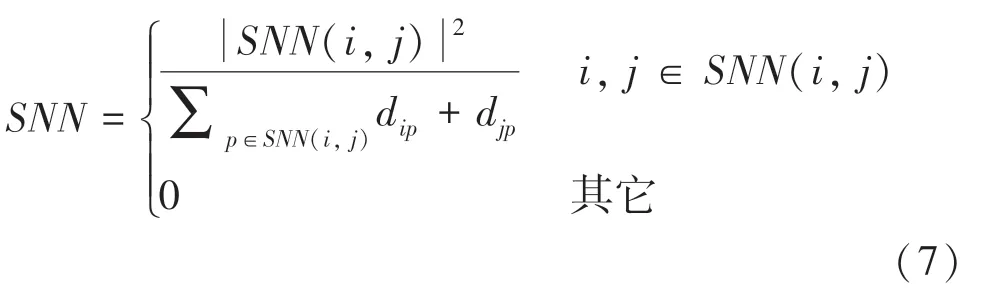
1.4.2 第一截断法

为了更有效地合并子簇并减少获取数据的时间，在子簇合并的过程中使用“第一截断法”。该方法的原理是：通过2个簇合并的位置视为“第一个大跃变”，此时2个簇理论上最不相似，因此只需找到第一个大跃变位置，如此就能找到最适合的分簇。可将合并后的层级视为自下而上的树状图，将树状图从中间划分为上、下两个部分，不断切割直至找到第一大跃变点作为合并图的最优截断数据，该数据即为数据集的最优分簇，具体代码详见算法3。

合并图

合并图的最优截断高度

1： Procedure（，）

2：_（）

3：（）

4：while0 do

5：_（*）

6： If

7： return

8： else

9：

10： End if

11：End while

12：_（）

13：（）

14：For alldo∈

15：

16： Ifthen

17：

18：

19： Return

20： End If

21：End for

22：

23：Return

2 KSNN-Chameleon实现

KSNN-Chameleon算法与传统算法均分为3个阶段，传统的Chameleon算法在针对二维Q型算法时，能够得到良好的聚类效果。但其算法在面向如“宿舍分配”等多维R型聚类问题时，难以维持二维情况下的精准聚类。因此本算法在传统算法的各个阶段都进行了不同程度的改良，使得改良后的算法在面对高维度的R型聚类问题时也能取得良好的聚类效果。

2.1 构建加权近邻图

KSNN-Chameleon算法以加权近邻图的方式代替原有的K近邻图作为数据集的稀疏图。首先采用KD树和K近邻算法相结合的方式，获取K近邻图，然后，根据公式（3）计算出每个点的相似度，再通过公式（4）和公式（5）计算出每个点近邻点集，得到由近邻点集构造出的加权近邻图。具体步骤如下所示。

初始数据集，分类参数

加权近邻图（稀疏图）

构建KD树，通过输入参数对相似度矩阵进行初始化。

从KD树的树根开始不断遍历，将所有数据划分在不同的区域当中。

根据数据集中的数据，利用定义3中的公式（3）算出每个点间的相似度，构建相似度矩阵。

在KD树的每个区域中取前个最相似的值分类更新相似度矩阵，得到K-最近邻相似矩阵。

利用算法1，分别求出不同值时得到相似矩阵情况，根据定义6、7计算数据点间的近邻权重，得到加权近邻图。

2.2 加权近邻图的划分与合并

在KSNN-Chameleon算法的第二阶段和第三阶段中，对加权近邻图进行图划分时，首先利用递归二分法和洪水覆盖法（flood-fill）对稀疏图进行图划分如算法2所示，然后采用定义10中的公式（7）计算出共享相似度，对图划分后得到的子簇进行自下而上的层次聚类，此时可以得到数据集的合并树状图。此后采用算法3中的第一截跳法求出适合于数据集的最佳聚类数，反复合并划分图直到满足最终簇数完成聚类，具体步骤如下所示。

加权近邻图，聚类簇数

个簇的聚类

将加权近邻图带入算法2中，利用flood-fill方法对加权近邻图进行图划分，得到分簇。

结合定义10中公式（7）求出各个子簇之间的共享相似度，推算子簇之间的相似关系。

通过共享相似度对数据集进行自下而上的层次聚类，并将聚类结果视为树状图。

将树状图带入算法3中，利用第一截断法求出聚类簇数。

将得到的簇数与聚类簇数对比，若不同则返回Step 2；若相同，则此时的聚类结果即为最终的聚类结果。

结合KSNN-Chameleon算法三个阶段所绘制的大致流程如图3所示。

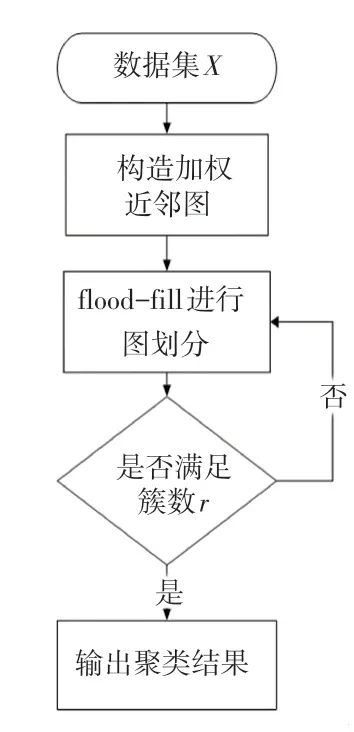
图3 KSNN-Chameleon算法总流程Fig.3 Flow chart of KSNN-Chameleon algorithm

3 实验数据分析

3.1 KSNN-Chameleon评估

为验证KSNN-Chameleon算法的可行性，本文采用Matlab测试数据集中具有代表性的4个测试数据集、即Aggregation、Iris、Seeds、Wine数据集对改良算法进行测试，并通过几种聚类评估的基准验证KSNN-Chameleon算法对于高维度的数据集具有良好的聚类效果。在与传统算法进行对比后得到的聚 类结果见表1。

表1 不同维度下2种算法聚类对比Tab.1 Clustering comparison of two algorithms in different dimensions

KSNN-Chameleon算法针对Aggregation二维数据集聚类后的结果如图4所示，在面向二维数据集时，KSNN-Chameleon算法与传统算法得出的结果图基本一致。图5为Iris（四维数据集）在三维空间中的展示图，通过对比后证明在高维聚类的情况中，KSNN-Chameleon算法比传统Chameleon算法的聚类更加完善，其中聚类精度平均提升了20.88%，聚类时间平均提升了2.73%。实验证明在面对R型高维度聚类问题时，KSNN-Chameleon算法仍然能具有较好的稳定性与聚类精度。

本实验对289名在校学生进行调研，并将数据整理为表，见表2。结合图4、图5和表2中数据可看出，对于二维数据集而言，KSNN-Chameleon算法的聚类精度没有明显地高于传统Chameleon算法，仅仅是略高于传统型。但当数据集的维度变大时，传统Chameleon算法的聚类效果明显下降，而改进型则有了显著的提升，即KSNN-Chameleon算法更适用于高维度聚类。在对比二者所消耗的时间时，发现KSNN-Chameleon算法和Chameleon算法所消耗的时间几乎没有很大的差别。但在二维以上环境中，KSNN-Chameleon算法所消耗的时间还是略小于传统算法的，这是由于在稀疏化阶段，KSNNChameleon算法为了更好地适应高维聚类，在传统算法只使用K近邻图的基础上，又对数据进行了近邻加权的操作，所以增加了时间的消耗。同时，该算法为了抵消这一部分操作带来的时间影响，在K近邻法中又增加了KD树的概念，减少了部分内存和时间的多余损耗，甚至在高维情况下还有一定的提升。

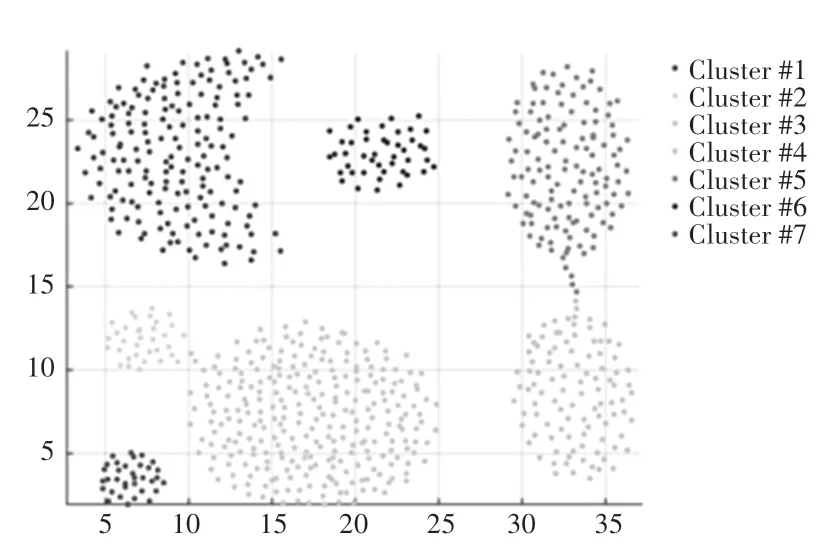
图4 KSNN-Chameleon算法对Aggregation数据集聚类结果Fig.4 The clustering results of Aggregation dataset using the KSNN-Chameleon algorithm

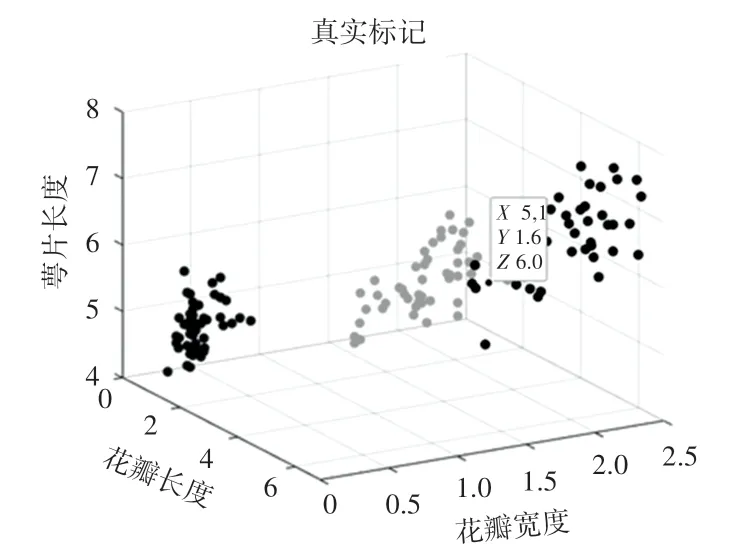
图5 KSNN-Chameleon算法对Iris数据集聚类结果Fig.5 The clustering results of Iris dataset using the KSNNChameleon algorithm

表2 StuData信息Tab.2 StuData information

3.2 实验条件和数据来源

实验测试采用的硬件环境如下：CPU为i5-8300H，内存为8 GB。运行环境为Windows 10操作系统。软件环境为IntelliJ IDEA 2020.3.4 x64、Matlab2020b。语言为Matlab、JAVA。

3.3 数据集稀疏化

以Matlab中的二维数据集Aggregation和学生调查的五维数据集StuData为例，将二维数据集Aggregation展示在二维平面中，StuData作为五维数据集将其中3个特征向量的数据抽取出来展示在三维坐标系中。结合第1节中的稀疏化步骤，针对数据集Aggregation取值为10，然后通过传统Chameleon算法以相似度计算得到的近邻图如图6（a）所示，通过改进型Chameleon算法得到的加权近邻图如图6（b）所示，可以看出两者在同样的值和二维环境中得到的近邻图相似。按照同样的步骤，在五维数据集StuData中取值为10后，通过传统算法得到的近邻图如图6（c）所示，而通过KSNNChameleon算法得到的加权近邻图如图6（d）所示。

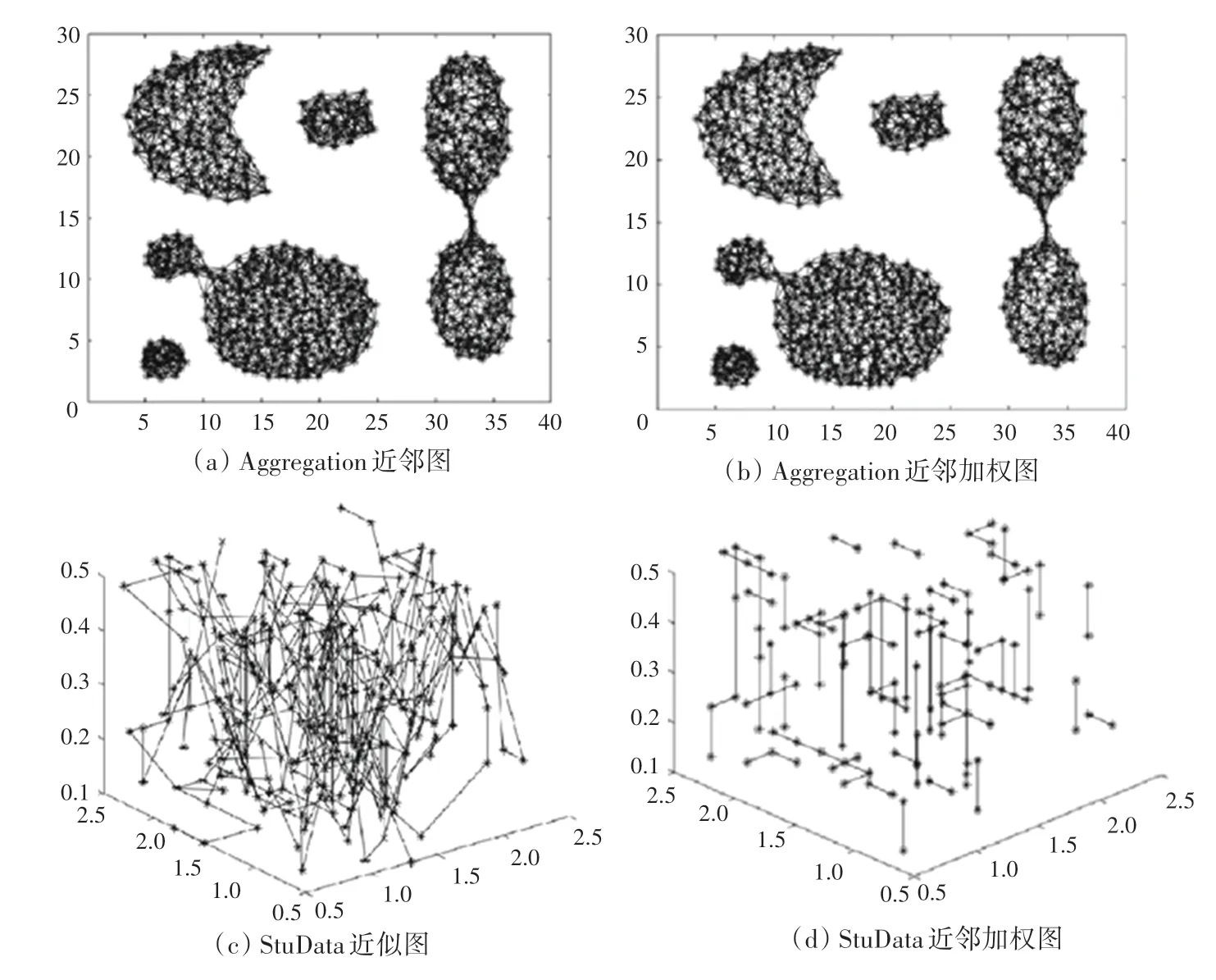
图6 对不同数据集使用传统算法和改进算法稀疏化Fig.6 Using the traditional algorithm and the improved algorithm to sparsely process different data sets

由图6可以看出在高维度情况下，KSNNChameleon算法的稀疏化结果更加精确，并且没有出现远点聚类情况。

3.4 通过KSNN-Chameleon宿舍分配

本文通过问卷调查的形式访问了289名在校学生的共7项意愿，从而整理得到了五维数据集StuData。在通过对每一项指标详尽的分配权重后，对其采用多种不同形式的聚类算法进行聚类，模拟出宿舍分寝情况。采用聚类评估的方式，对这些聚类方法进行评估，验证这些算法在面对高维聚类时的性能优劣，对比结果见表3。

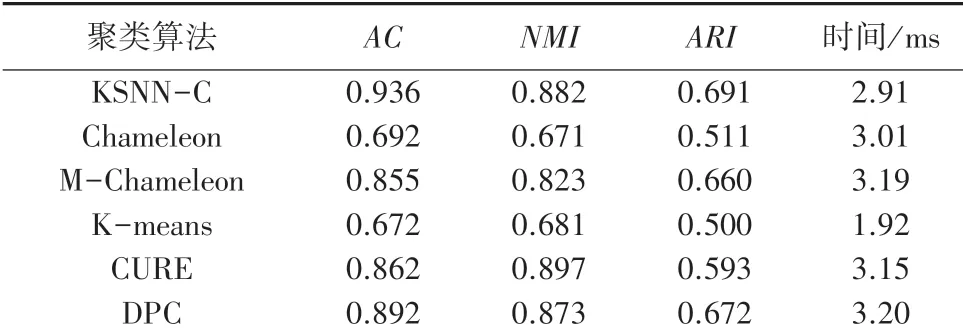
表3 采用不同算法对StuData进行聚类Tab.3 Clustering StuData with different algorithms

由表3可看出，将KSNN-Chameleon算法与目前几种主流聚类算法，包括：传统Chameleon算法、M-Chameleon算法、K-means、CURE、DPC算法，进行对比发现，针对五维数据集StuData和KSNNChameleon算法的聚类精度是最高的。对6种算法的值进行对比后，发现KSNN-Chameleon算法除了略低于CURE算法外，值都高于其它算法。对测试数据集重叠程度进行测量的值进行比对后，发现KSNN-Chameleon算法依然拥有良好的表现，仅略低于DPC算法。在聚类时间上，由于KSNN-Chameleon算法在聚类过程中需要对稀疏图进行加权，所以运行的时间也相对延长了。对比传统Chameleon算法，KSNN-Chameleon算法的聚类精度平均提升了0.165，值平均提升了0.205，值提升了0.181，在面对高维R型聚类问题时明显更加稳定，证明在高维环境中KSNN-Chameleon算法能够进行更有效的聚类。

在对比多种算法后，本文采用KSNNChameleon算法对StuData的数据图和聚类结果图进行分析，图7为三维环境中展示数据集StuData的所有数据点，图8为使用传统Chameleon算法对数据进行聚类后的结果图。图9为通过KSNNChameleon算法对数据集进行聚类后的结果图。通过图8和图9的对比可以看出，通过KSNNChameleon算法得到的聚类图相较Chameleon聚类得到的结果聚类图更加均匀，每个簇中的数据也更加平均和接近。证明KSNN-Chameleon算法对传统算法的改良是有效的。

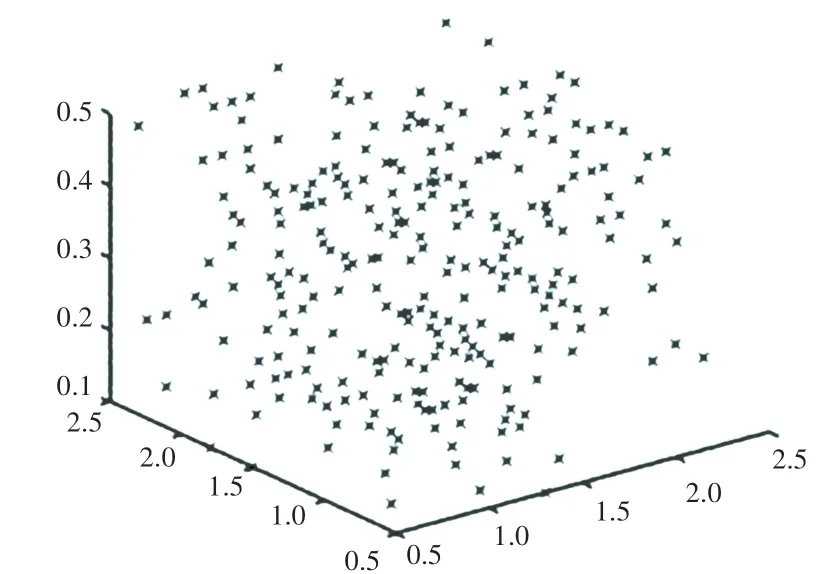
图7 StuData三维环境中数据图Fig.7 Data graph of StuData in 3D environment

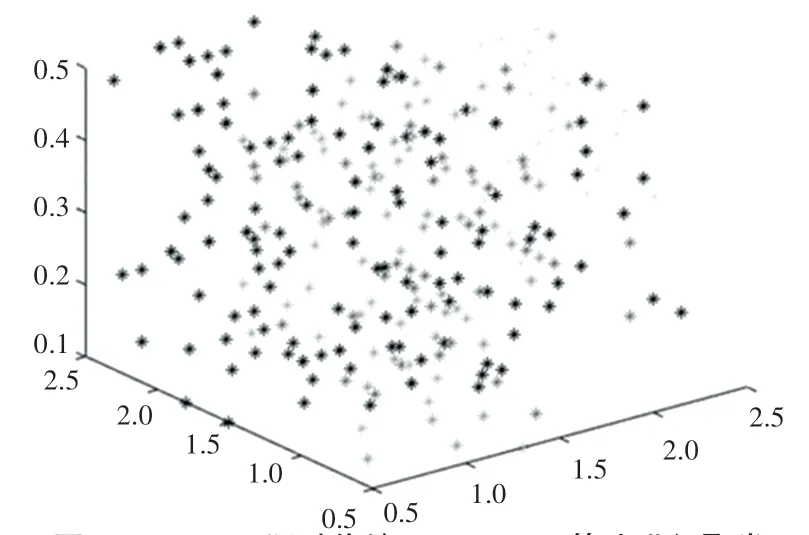
图8 StuData通过传统Chameleon算法进行聚类Fig.8 StuData clustering by traditional Chameleon algorithm

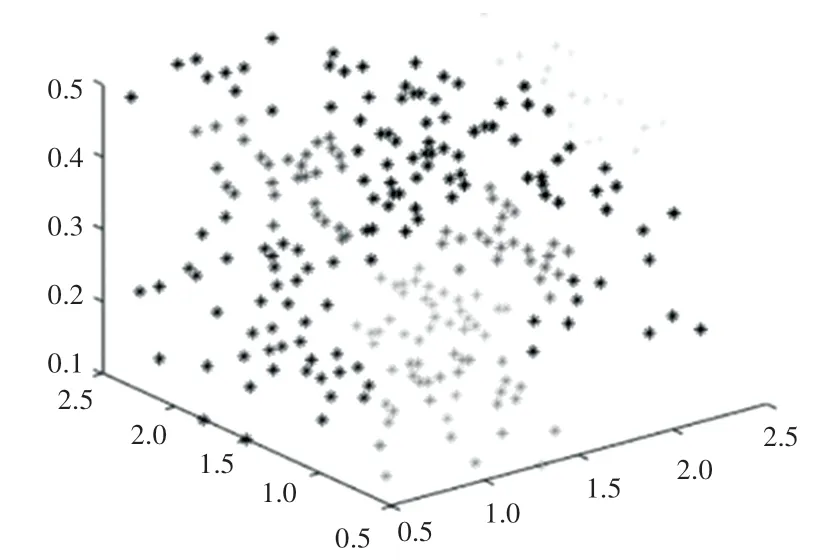
图9 StuData通过KSNN-Chameleon算法进行聚类Fig.9 StuData clustering by KSNN-Chameleon algorithm

研究针对StuData数据集中289名学生进行聚类后，将每一簇的学生按照每4人一组模拟为一个宿舍，绘制成宿舍分配表发放到这289名学生手中，并再次对学生进行调研回访。在289名学生中有65.05%的学生愿意按照此宿舍分配表的方式进行换寝，另外34.95%的学生认为维持原有的宿舍分配也不错。

4 结束语

本文针对传统的Chameleon算法进行改进，提出基于加权近邻法的KSNN-Chameleon算法，在针对R型高阶聚类问题时能够有着良好的聚类效果。算法首先在聚类的稀疏化阶段采用了加权近邻图的方法，有效避免了在R型聚类中使用距离为参照标准的问题。然后用洪水覆盖法（flood-fill）代替原有的hMetis算法，对加权近邻图的处理更加地细腻。最后利用共享近邻相似度和第一截断法，使得在高维环境中也能更好地将数据进行聚类，而不出现分散的问题。分析可知，KSNN-Chameleon算法在聚类的准确率和精度方面对比传统算法均有所提高。KSNN-Chameleon算法对比传统Chameleon算法的聚类精度提升了20.88%，聚类时间上则提升了2.73%，由此证明KSNN-Chameleon算法在面对高维R型聚类问题时更加稳定。