基于机器学习的乘用车上坡动力学建模研究

葛阳洋，范平清

（上海工程技术大学 机械与汽车工程学院，上海 201620）

0 引 言

研究可知，无人驾驶是人工智能领域的热点科技课题之一。研究初期，只有为数不多的几个发达国家在该领域展开角逐，随着中国科研基础和工业技术的发展、完善，在政府的支持下，国内的一些高科技公司和多所高校也已陆续开启了对无人驾驶的探索和讨论，并取得了可观的研究成果。虽然在路试中暴露了不少缺点，但却为此后的研究奠定了坚实的基础。

本文的研究内容方向是无人驾驶领域中的一个重要分支，通过数学建模的方法来模拟汽车上坡过程，将乘用车上坡过程数字化，并通过编程导出关键数据。后续用到的BP神经网络是机器学习衍生出的一种算法，不仅具有结构简单、使用方便等特点，而且在Matlab工具箱中还有自带的BP神经网络工具，因此可以直接在Matlab上进行调用来训练建模产生的数据，优化动力学模型，实现重要参数的分配。在研究过程中提出了有关无人驾驶的新思路，进一步开拓了智能驾驶领域的研究。

1 动力学建模

从汽车上坡过程的阻力部分入手，接着引入附着条件，然后根据发动机转矩拟合结果对驱动力部分进行处理，最后对各个部分的建模进行汇总，并不断完善和修改模型，直至符合车辆动力学要求。动力学建模的流程如图1所示。

图1 动力学建模流程图Fig.1 Flow chart of dynamics modeling

1.1 汽车行驶方程拟定

乘用车上坡过程涉及多个参数，汽车行驶方程式可写为：

式中各部分有：

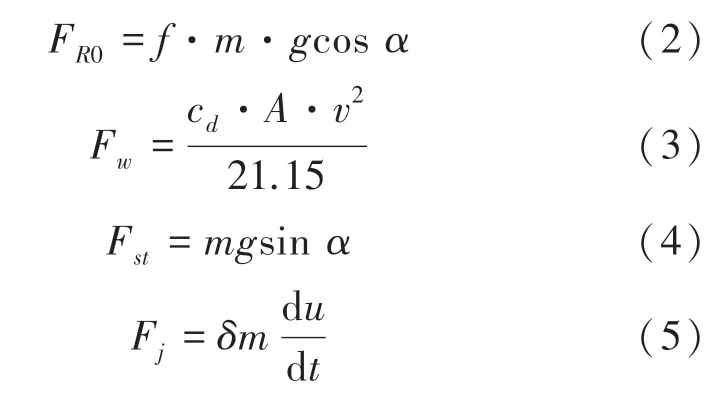
其中，F为驱动力；F为滚动阻力；F为空气阻力；F为坡度阻力，即重力下滑分力；F为加速阻力（F、F、F、F、F的单位均为N）；为整备质量，单位为kg；为当地重力加速度（取9.8 m/s）；为滚动阻力系数；C为空气阻力系数；为迎风面积（选定车型计算得2.442 m），为汽车行驶速度；为该乘用车的旋转质量转换系数（此车型是1.2）。

1.2 驱动力的确定

乘用车行驶过程中对驱动轮有一摩擦力，此摩擦力的反力F驱动乘用车行驶，研究推得的数学公式为：

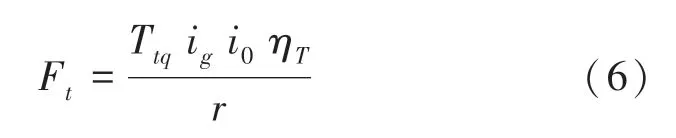
其中，F是发动机转矩通过汽车传动系后传递到驱动轮的转矩；为车轮半径；T为发动机转矩；i为变速器的传动比；为主减速器的传动比；η为传动系的机械效率，该车型为089；对于该车型的发动机有厂家给定测试转矩数据，见表1。

表1 发动机转矩实测数据Tab.1 Measured data of engine torque

将转矩数据在Matlab上进行多项式拟合，由此可得发动机转矩与转速关系为：

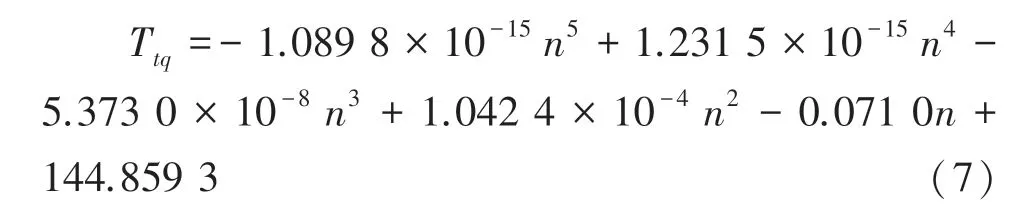
由公式（7）得到选定车型发动机转矩性能如图2所示。

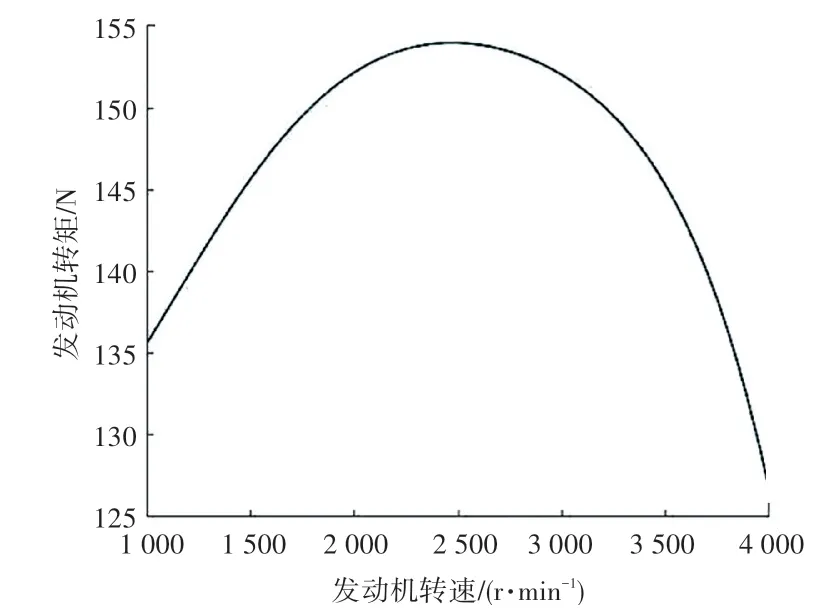
图2 选定车型发动机转矩性能拟合Fig.2 Fitting of engine torque performance for selected vehicle types

1.3 汽车行驶的附着条件

图3是乘用车上坡受力分解的简单示意。汽车行驶的附着条件是：

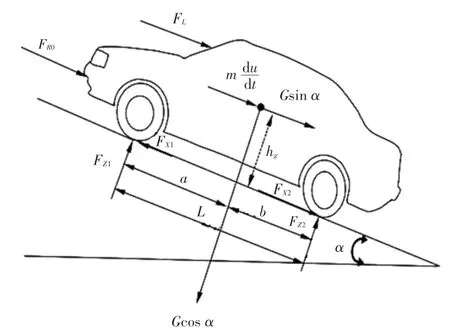
图3 乘用车上坡受力分解Fig.3 Decomposition of uphill forces for passenger vehicles

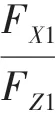
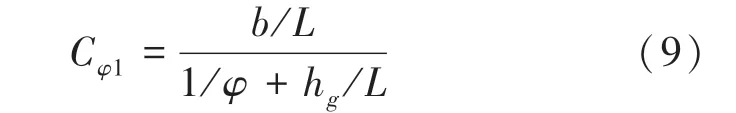
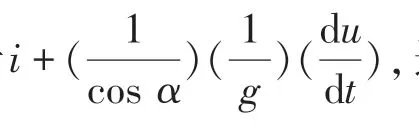
1.4 模型总结

该车发动机与车速的关系式为：

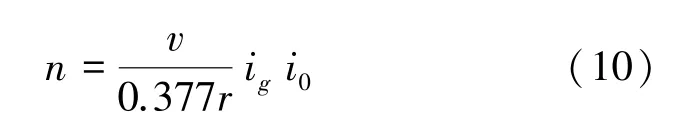
其中，为是汽车行驶速度；是发动机转速；为车轮半径，是0.328 4 m；二档时，i为2.816；为4.788。

乘用车上坡时所受空气阻力和发动机转速的关系为：

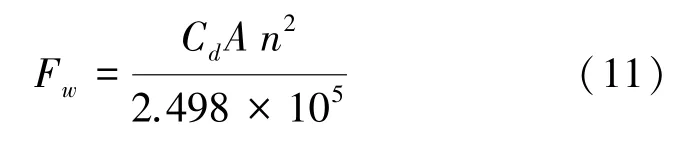
将式（7）、式（11）在Matlab计算后得出该车发动机转速和驱动力的关系式：

其中，为1089 810；为1231 510；为5373 010；为1042 410；为-0.071 0。

2 输入输出参数的处理

2.1 确定输入输出参数

影响乘用车上坡过程的因素有汽车内部因素—发动机的转速，外部因素主要是道路的条件，如道路的坡度、滚动阻尼等，由此拟定以下输入变量：坡度、发动机转速、路面附着系数、路面滚动阻尼。

为衡量车辆上坡时的性能，拟定以下输出变量：驱动力F、车辆加速度（负数表示不能持续爬坡）、可通过的最大等效坡度、轮胎是否打滑判定（输出1表示不打滑，输出0表示打滑）。

2.2 建模过程的数据导出与处理

后续编程用到的选定车型的基本参数见表2。

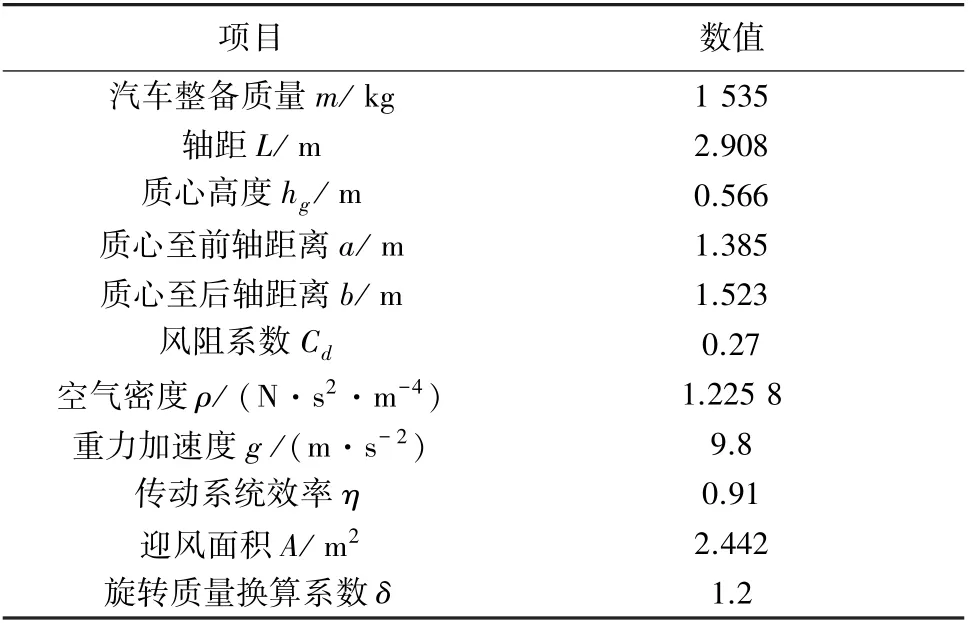
表2 基本参数Tab.2 Basic parameters

根据第一节所建立的车辆上坡过程动力学模型，通过Matlab编译出乘用车在上坡过程中产生的各个数据，编程算法代码具体如下：

将根据动力学建模运行处理后的数据保存成Excel表格，用于后续的数据训练与BP神经网络学习。

3 BP神经网络训练与预测

根据下面经验公式选取层数，即：

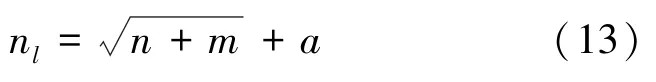
其中，n是BP神经网络的隐含层节点数量；是神经网络输入层节点数；为神经网络输出层节点数；为1～10之间任意常数。计算后得出本模型的n为10。

调用Matlab工具箱的BP神经网络对第二节导出的数据进行训练，训练流程见图4。

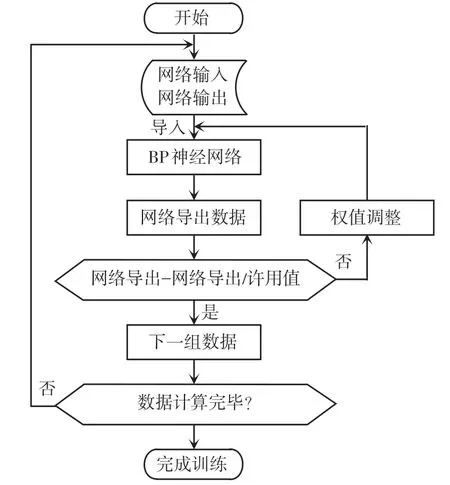
图4 数据训练流程图Fig.4 Flow chart of data training

图5 是在Matlab进行车辆上坡过程动力学建模中BP神经网络训练时的参数设置，包括训练步长、梯度、最小误差范围等。图6是经过训练后形成的神经网络的10个隐含层的各个权值情况，各个隐含层的权值在数据的训练中不断进行调整，使得神经网络进一步得到优化。

图5 训练参数设置Fig.5 Setting of training parameters

图6 隐含层权值Fig.6 Weights of the hidden layer

图7 是基于均方误差计算并绘制出来的曲线图。均方误差（mean-square error）的变化可以体现出模型预测情况与实际情况的差异程度。由图7可以看出，随着训练的进行，误差大体沿着越来越小的方向进行变化，从最开始数百万的误差变成了只有百分之一级别的误差，训练优化了动力学模型。

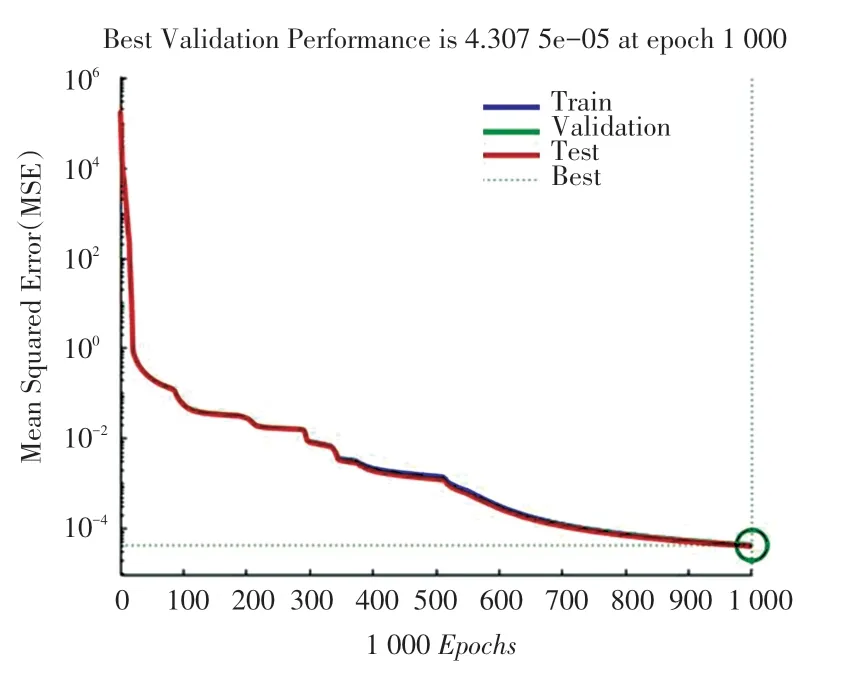
图7 训练误差表现Fig.7 Performance of training errors

4 结束语

本文提供了车辆动力学建模的思路以及简便处理动力学建模数据的方法，并基于BP神经网络对建模数据进行训练，使得模型网络化，优化简便了动力学模型，同时也大幅度减小了模型的表现误差，这就为智能驾驶的建模及数据处理提供了新的思路。