受强化学习思想启发的一种结构优化算法

李 徐，张 帆

（上海工程技术大学 机械与汽车工程学院，上海 201620）

0 引 言

结构工程中的大多数设计优化问题都是高度非线性的，在复杂的约束条件下涉及许多不同的设计变量，这些约束可以写成简单的界限，如材料特性的范围，也可以写成非线性关系，包括最大应力、最大挠度、最小承载能力和几何形状，这种非线性经常导致多模态响应景观，所以在结构优化问题中，寻求最优参数就变得更加困难。

强化学习的思想来自于条件反射理论和动物学习理论，是一种受到动物学习过程启发而得到的仿生算法，是重要的机器学习方法，因为其具有良好的无监督学习能力，该算法主要被运用于机器人领域以及人工智能领域，在结构优化问题中几乎没有被提及，这是因为如果套用整个的强化学习算法模型，则无法运用在结构优化问题中，但是基于结构优化问题中的设计参数和界限函数与强化学习中的动作、状态很相似，选择某一组设计参数就会对应某一个确切的界限函数值，在强化学习中选择某一动作后转移到某一个状态是一个概率事件，而结构优化问题中是确定性事件，也可认为转移的概率为1，在强化学习中目标是要找到奖励值最大的策略，而在结构优化问题中，只要找到可以使目标函数最优的设计参数就行，而设计参数的测试与选取也是靠某种策略得到，因此可以将强化学习的动作状态转移模型转换到结构优化寻优中来，更详细的说明在算法原理中有介绍。

布谷鸟搜索（Cuckoo Search，CS）是一种新的元启发式搜索算法，这个算法是基于一些杜鹃物种的专性繁殖寄生行为，结合了一些鸟和果蝇，是由Yang等人开发的，初步研究表明，该算法的应用前景很广，优于现有的遗传算法和粒子群算法，因此在本案例中，用布谷鸟搜索（CS）算法去验证所提出的优化算法，证明了该算法的可行性。本文的工作主要分为以下3个部分：

（1）算法原理中，介绍了该算法的原理，以及算法流程。

（2）案例验证中，用纯数学问题和工程案例去验证该算法的可行性。

（3）结果与讨论中，分析了实验仿真的结果，同时说明了该算法的局限性。

1 算法原理

在算法中，采用神经网络作为策略函数，因其具有极强的泛化能力、非线性映射能力，以及高度的非线性并行性，研究时常被用来作为一种学习器，并广泛运用于图像识别、分类应用中。在强化学习中也充分利用了其特性来作为策略函数，以解决具有连续动作和连续状态的强化学习，例如Policy Gradient（PG）、Proximal Policy Optimization（PPO）、Deep Deterministic Policy Gradient（DDPG）等。基于此，在本次研究中，采用了神经网络作为策略函数，单层的神经网络模型如图1所示。

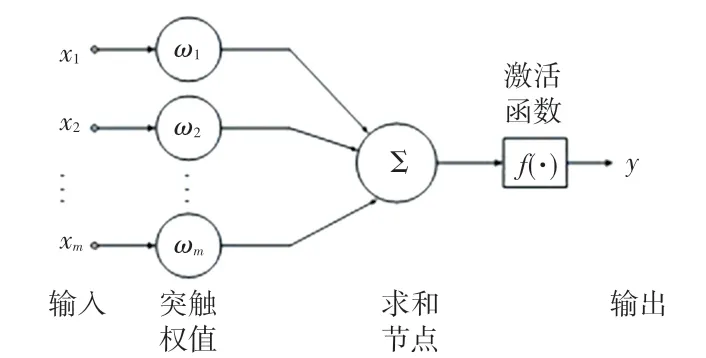
图1 单层神经网络模型Fig.1 Single-layer neural network model

由图1可知，图1的输出值为：

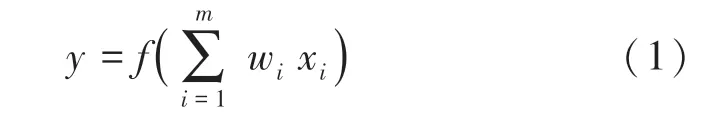
神经网络的更新方式是通过反向传播、梯度下降的原理去更新神经网络的参数，其更新方式的数学原理如下。

设输入样本为：

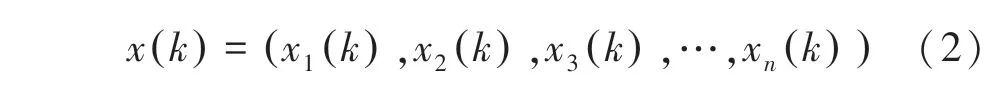
期望输出为：

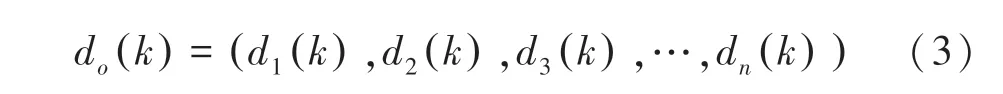
隐藏层各神经元的输入输出如下：

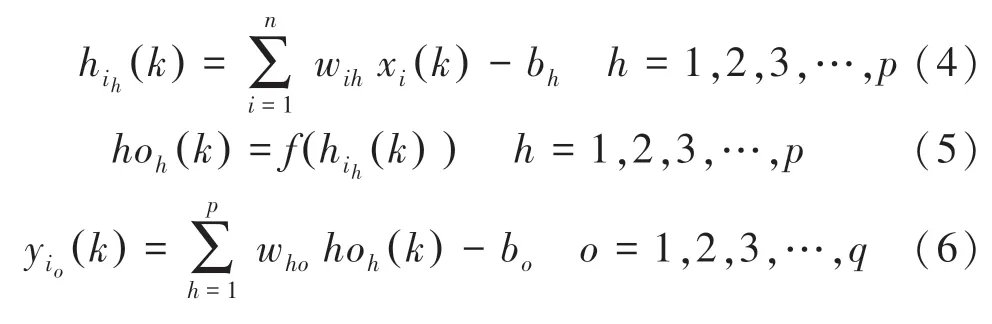
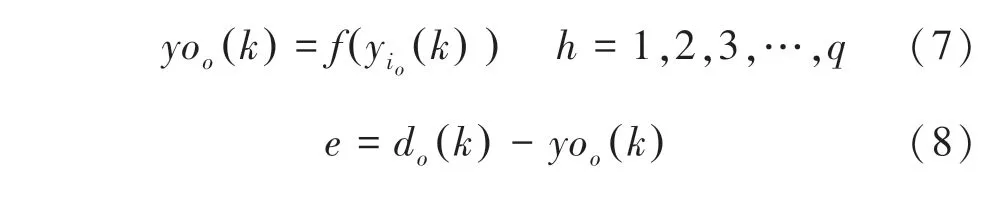
求出期望值d k()与实际输出值yo k()的误差函数的偏导数δ k()，其公式如下。

输出层可写为：

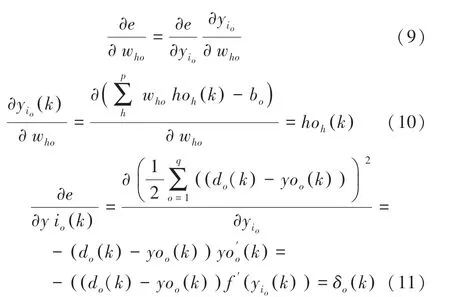
隐藏层可写为：

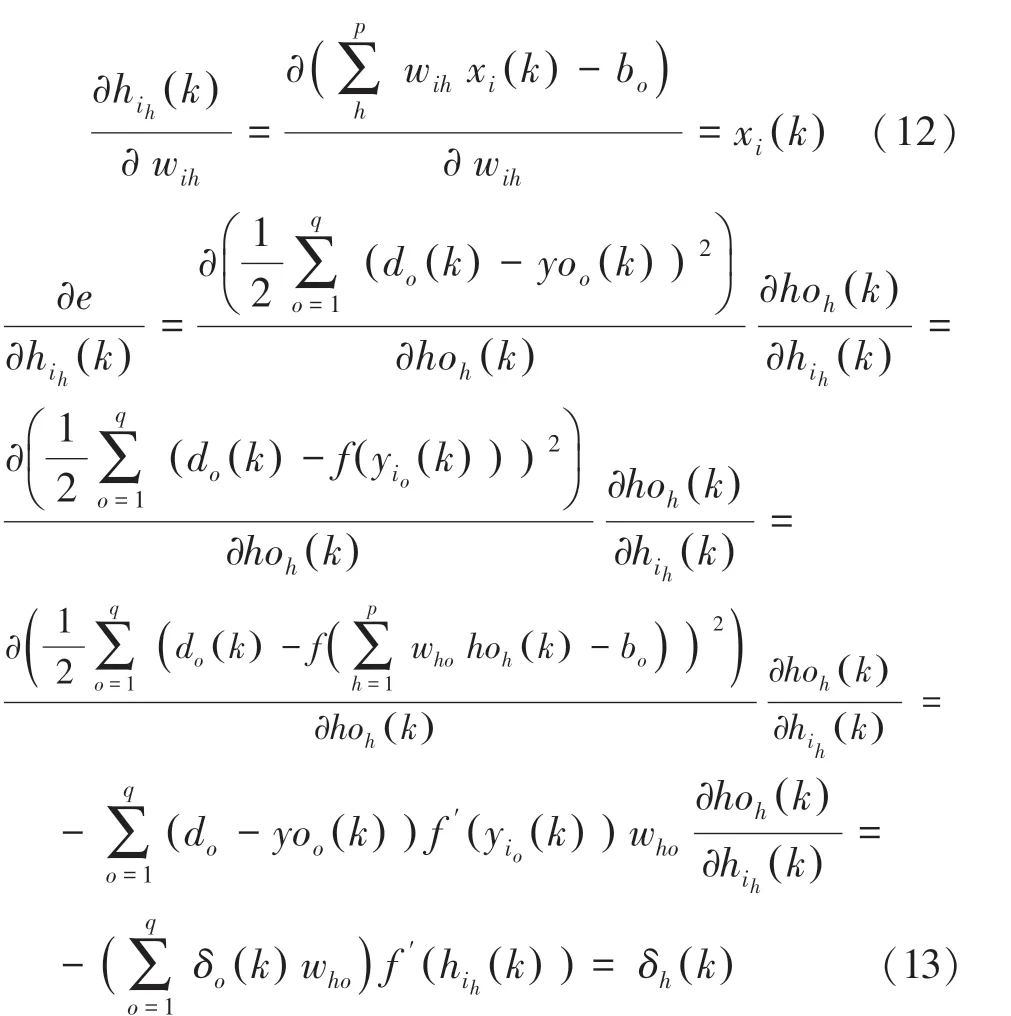
利用输出层各神经元的δ k()和隐藏层各神经元的输出来修正链接权值w k()。 研究中推得的数学公式可表示为：

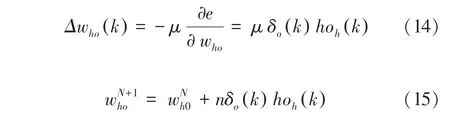
利用隐藏层各神经元的δ k()和输入层各神经元的输入修正权连接。研究中推得的数学公式可表示为：

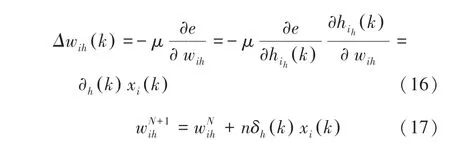
其中，是学习率。

通过式（17）就可以实现梯度下降，从而找到最优的目标函数值。

对于一个工程或机械结构优化问题，会涉及到设计参数，需要优化的目标函数（），以及会因为参数改变而引起其他性能变化的函数，在这里称为界限函数（），一般会要求（）在某一范围内。

虽然该算法启发与强化学习，但是在寻优的过程中没有正向意义上的奖励值，而是用优化机会作为奖励值，只要满足某一状态就可得到一次优化的机会，在强化学习中使用了基于神经网络的强化学习算法，如PPO、DDPG算法。在训练神经网络时，是对一批数据输入进行训练，这是由强化学习的算法决定的，现实中均值是无法确定的，需要通过求平均值来近似均值，而在结构优化中，只是要找到满足界限函数这一状态下的最优目标参数这一动作值即可，因此用本文提出的算法只能一次输入一个状态值（界限函数）到神经网络中，得到什么样的权重参数不重要，重要的是得到的设计参数是否是最优。

在提出的算法中，运用了强化学习的状态转移和策略函数的思想，以及神经网络的特性去优化目标函数，在有界限函数（）的情况下找到最优解的前提是其设计参数必须先满足界限函数，因此首先要找到满足界限函数的参数空间位置，然后在这个参数空间中寻找最优的目标参数。在该算法中，先随机选择一组满足界限函数的初始状态，用该状态作为神经网络的输入，其输出是该状态下选择的动作（设计参数），将该动作作为界限函数的自变量，计算出下一个状态（），与强化学习中的状态定义不同，这里将满足界限函数值这一类作为一个状态，不满足作为另一个状态，如果下一个状态在界限函数范围中，将该状态作为新的神经网络的输入，通过反向传播，梯度下降优化目标函数，如果超出了界限函数的范围，就以上一次的状态作为新的输入，通过反向传播、梯度下降的方式去更新动作输出，直到输出的动作值在界限函数值的范围之内，重复以上过程，直到训练结束，算法流程如图2所示。

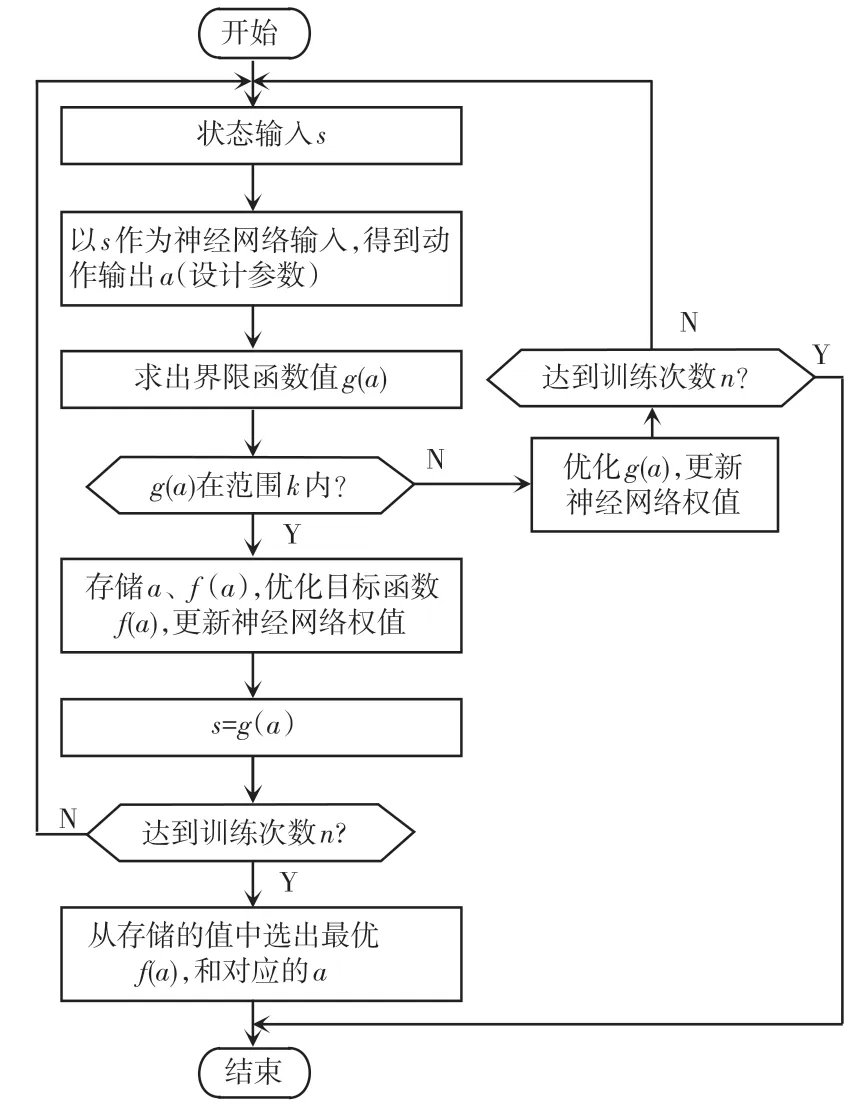
图2 算法流程图Fig.2 Algorithm flow chart

2 案例验证

2.1 纯数学问题验证

为了验证该算法可以找到最优解，考虑如下一个数学问题，有4个参数（，，，），∈[0，4]，∈[0，5]，∈[0，4]，∈[0，6]，有函数：

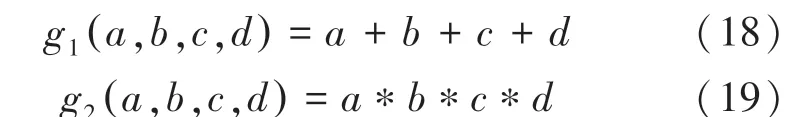
求在(，，，)≤9，(，，，)≤20的情况下函数（，，，）的最小值：

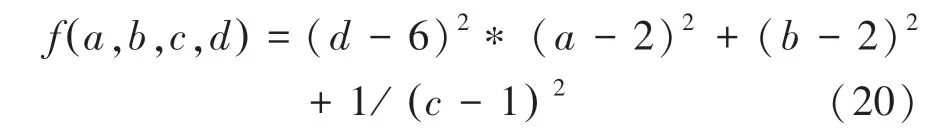
可以知道，在不考虑，的情况下可以取值6，取值2，取值4，而可以任意取值就可得到最优解；当考虑，的情况下，明显不能取值6，取值2，取值2，取值4同样可以得到最优解。通过所提出的算法求得其参数见表1，和预想的结果几乎一样，同时在相同运算时间内比使用CS算法得到的值更精确。

表1 实验数据Tab.1 Experimental data

该数学问题的目标函数不是很复杂，满足，的参数空间占比较大，且连续，可以看见收敛过程非常快（见图3），值与，相对应的散点三维图见图4，很明显在目标函数值下降的过程中，最小值对应的点越来越集中。

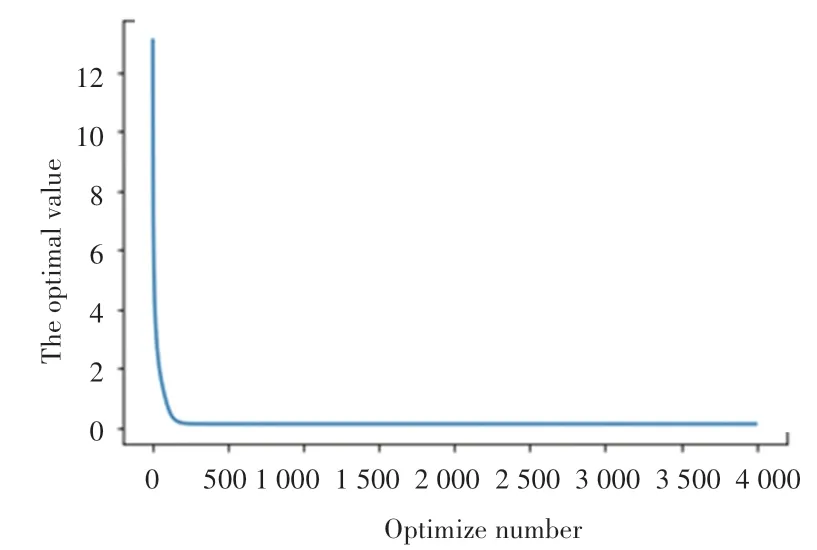
图3 收敛过程Fig.3 Convergence process

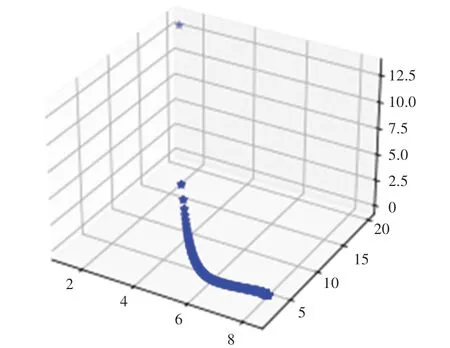
图4 散点图Fig.4 Scatter plot

2.2 工程实例

最小化工字梁的垂直偏转：使用一个包含4个变量的设计问题来测试该算法，此案例来自报告中的原始问题（已修改），目标是最小化工字梁的垂直偏转（见图5）。梁的相关参数：5 600 kN，550 kN。并且同时满足给定载荷下的横截面积和应力约束。当梁的长度（）和弹性模量（）分别为5 200 cm和523 104 kN/cm时，最小化垂直挠度（）48。 因此，该问题的目标函数可写作如下形式：

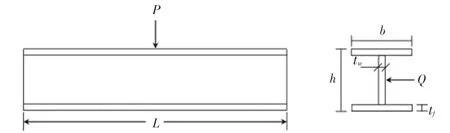
图5 梁结构Fig.5 Beam structure

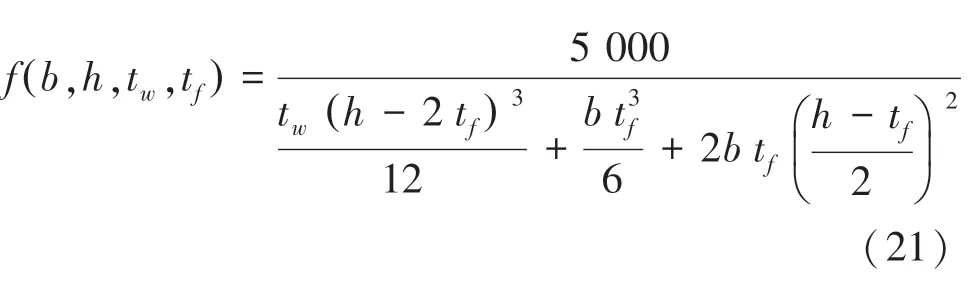
以横截面积小于300 cm为基准，有：

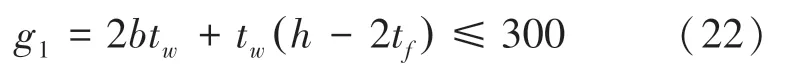
如果梁的容许弯曲应力为56 kN/cm，应力约束如下：

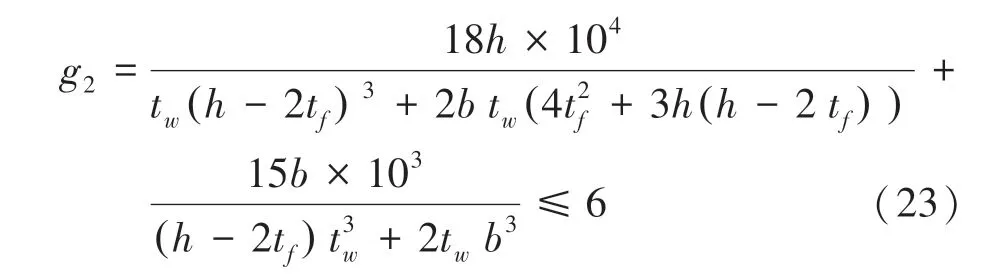
其中，设计参数空间满足10≤≤80，10≤≤50，09≤t≤5，09≤t≤5。

目标函数最终是收敛的（见图6），在近乎相同时间内该算法得到的最优值和相关参数与布谷鸟搜素算法得到的值见表2。为了排除该算法得到的最优值具有偶然性，运行得到了其他3组数据，仿真结果显示目标函数收敛在同一值附近，如图7所示。

表2 本文提出的算法与布谷鸟搜索算法得到的数据对比Tab.2 Comparison of the results between the proposed algorithm in this paper and the Cuckoo Search algorithm

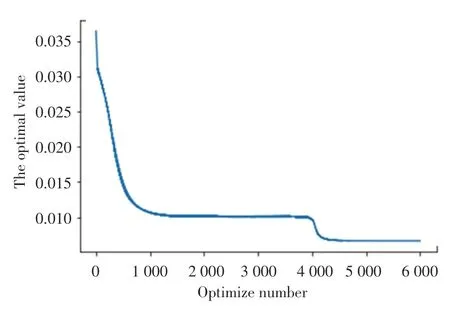
图6 收敛过程Fig.6 Convergence process

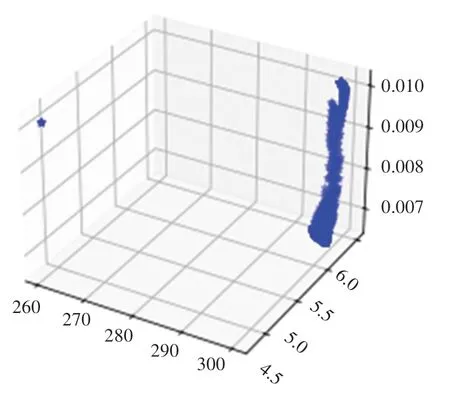
图7 散点图Fig.7 Scatter plot

3 结束语

实验仿真结果表明，在利用该算法寻优过程中，其目标函数值会因要考虑界限函数的值，可能出现一个振荡下降的过程（见图8），起初会有一个搜索阶段，这个阶段是为了寻找满足界限函数值的区域，当收敛到满足要求的界限值位置时，目标函数值会以一个相对光滑的趋势下降，直到收敛到最小值，呈现一条相对粗细一致的线条。从图8中可以看到，其收敛过程存在一定的差异，但最后都收敛到了最优值，经过分析发现，其原因就在于神经网络的初始化参数和初始化的状态值不同，较好的初始化位置，会使其在寻优过程中收敛曲线更加地平稳光滑，甚至会影响其收敛速度，因此可以认为，不同的初始化状态值和神经元参数对收敛过程具有一定的影响。

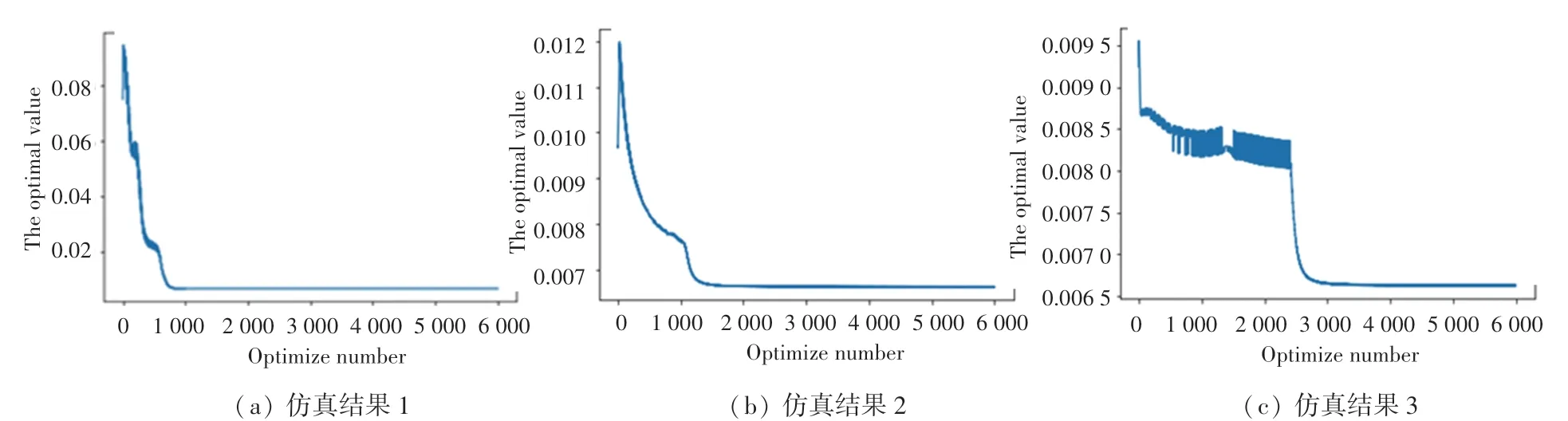
图8 实验仿真结果Fig.8 Experimental simulation results

另外，该算法具有一定的局限性，当满足界限函数的参数空间在整个参数空间占比较小，且位置较分散的时候，很难收敛到最优值，有时甚至无法收敛到满足界限函数的参数，这时需要不断改变初始值去求解最优值，同时如果面临参数空间中，有多个局部最优解的情况，此时初始化权值参数和初始化状态值没有选择到合适值，就可能无法找到全局最优解。但是对于全局最优解单一，满足界限函数的参数空间占比足够大的结构优化问题，该算法则可以更高效地找到最优解。