基于无偏灰色-马尔可夫模型的地铁牵引系统故障预测

张 程，李小波，张 浩，张冬冬，吴竑霖，汪 翔

（上海工程技术大学 城市轨道交通学院，上海 201620）

0 引 言

地铁车辆是城市轨道交通系统的重要载体，其运行的平稳性和可靠性关系到整个地铁交通系统的正常运转和乘客的人身、财产安全。而牵引系统是地铁列车的核心组成部分，是全车运行的动力源泉。因此，围绕列车牵引系统展开故障诊断和预测的研究对于提高列车的运行可靠性有着极其重要的意义。

目前应用广泛的故障预测方法主要包括：时间序列法、回归分析法、指数平滑法、结构分析法、灰色理论法、BP神经网络法等。牛坤等人针对铁路客流量时序特征明显的特点，采用基于平稳时间序列的铁路客流量预测模型对短时旅客客流量进行预测，对改善铁路运营压力具有一定意义。邓力等人在回归预测模型的基础上，提出一种网络组件故障的多元线性回归预测模型，并利用回归方程和系数的显著性得到新的预测方程，预测精度明显提高。杨博帆等人提出了一种能够根据历史数据计算出预测误差，并动态调整平滑系数及融合权值的在线预测算法，实现了对测量参数的准确预测。黄魁等人利用Levenberg-Marquardt算法改进神经网络模型，并与灰色模型相融合构建灰色神经网络故障预测组合模型，有效解决了故障样本数据少、预测精度低等问题。总结上述预测方法，可以将其分为2类。一类是根据采集到的各种特征量来评估设备或系统的运行状态；另一类是根据历史故障数据来预测设备或系统未来的故障发展趋势。但是，现有预测技术还存在诸多局限性。例如：时间序列法、回归分析法和神经网络法需要利用大量的历史数据，存在“周期长、区域大、信度低”的缺点，并且没有考虑数据波动性较大的情况。灰色预测方法虽然不依赖大量的历史数据，但在进行长期预测时精度会有所下降。与此同时，随着科技的不断发展和进步，各类设备和系统的性能日益提高，其复杂程度也急剧增加，导致故障预测的难度较大。因此，如何构建理想的预测模型、提高预测精度成为近些年来关注的热点问题。

针对以上问题，结合地铁牵引系统复杂程度高、数据样本少、随机因素多等特点，本文提出一种无偏灰色与马尔可夫模型相结合的预测模型。一方面，该模型既利用了灰色预测模型所需数据少、短期预测精度高的优点，对历史故障数据进行拟合并得出预测值；另一方面，考虑到系统故障次数具有随机波动性，通过马尔可夫模型寻找系统未来的故障状态变化规律，从而实现灰色理论与马尔可夫模型的优势互补。

1 无偏灰色预测模型

1.1 灰色理论

由于复杂装备或系统自身具有的复杂性和不确定性，常常导致监测数据不完善、数据样本少等情况，使得故障预测难度增大。针对这种“部分信息已知，部分信息未知”的灰色系统，一般使用灰色理论方法对其进行故障预测。

灰色理论的预测对象是系统行为特征值，也就是对在一定范围内变化的、与时间序列有关的灰过程进行预测。虽然系统数据看起来杂乱无章，但这些数据之间可能蕴含着潜在的规律。灰色理论就是在原始数据的基础上，通过生成灰色序列来寻求其变化规律。在此过程中，灰色序列的随机性被弱化，规律性逐渐显现。

整理分析地铁牵引系统故障数据资料发现，大部分数据包含的信息量较少，且规律性不明显，符合贫信息系统的特点，故选用灰色理论预测模型具有一定的适用性。但是，传统的灰色（1，1）预测模型适用于数据呈指数变化趋势的预测。因此，选用经过灰参数优化的无偏灰色预测模型，较好地解决了传统模型在数据增长率过高时失效的问题，提高了模型的预测精度。

1.2 无偏灰色模型建立步骤

（1）设原始数据序列为：

（2）累加生成新的数据序列：

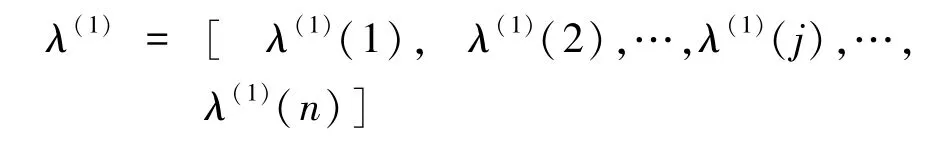
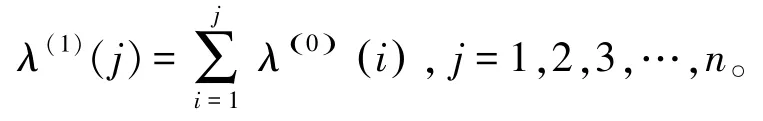
（3）构造累加矩阵和常数向量，生成的紧邻均值序列。由此推得的数学公式为：

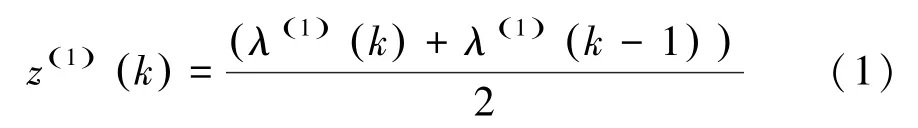
紧邻生成序列为：

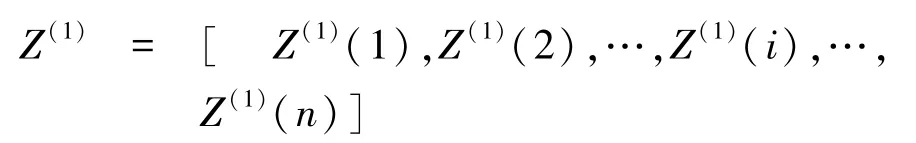
则存在累加矩阵和常数向量为：

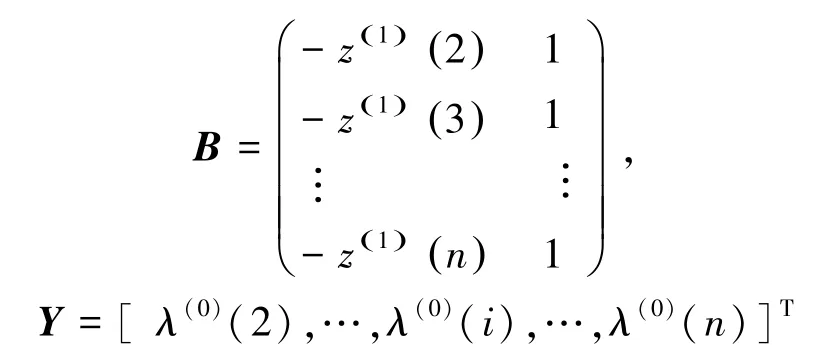
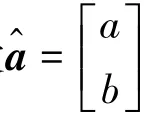
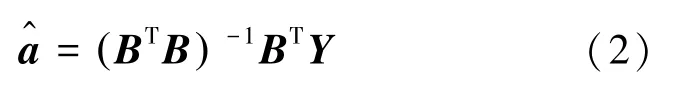
（5）在计算出、的基础上，再计算无偏灰色模型的参数、，其值分别为：

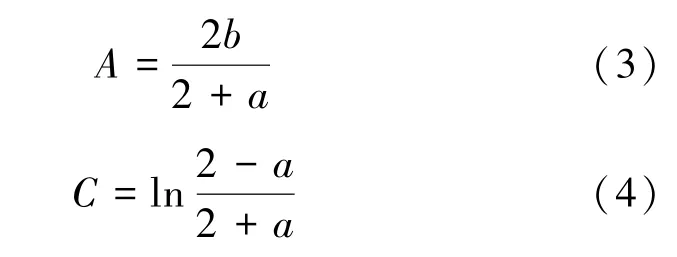
由此建立无偏灰色（1，1）模型：

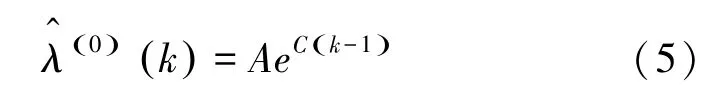
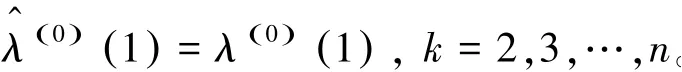
（6）模型精度检验。由模型预测函数计算出原始数据序列的拟合值之后，需要检验模型的预测精度，以便判断模型是否合理。本文采用平均相对误差、关联度和均方差比值这三项指标来对模型进行精度检验。 常用的模型精度等级检验参照表见表1。

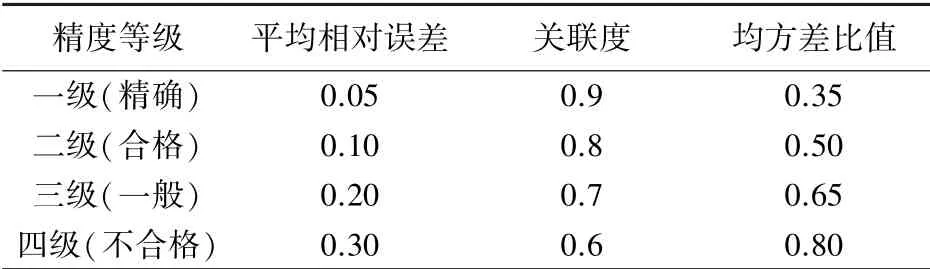
表1 模型精度等级检验参照表Tab.1 Accuracy grade inspection reference table for the model

2 无偏灰色-马尔可夫预测模型的建立

2.1 马尔可夫理论

马尔可夫理论的核心思想是：在随机过程中，系统在将来时刻的发展状态，仅与当前时刻所处的状态有关，而与之前状态无关，这个特性被称为“无后效性”或“马尔可夫性”，这个随机过程即为“马尔可夫过程”。

马尔可夫模型的预测对象是系统将来所处的状态，该理论以系统当前状态和变化趋势为基础，通过构建状态转移概率矩阵来寻找各状态之间的转移规律，最终计算出下一时刻系统向各状态的转移概率，故选用马尔可夫模型可以较好地应对数据随机波动性较大的情况，从而弥补了无偏灰色预测方法的不足。

2.2 无偏灰色-马尔可夫预测模型建立步骤

（1）划分状态。将无偏灰色模型的预测值与实际值相比较得出误差值，根据实际情况将其分为个状态，则任一状态区间可记为S＝［L，U］，，1，2，…，，其中L，U分别为该状态区间的上、下边界。

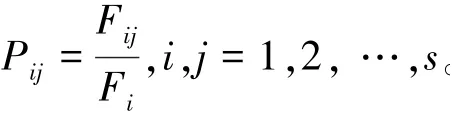
（3）预测系统状态。在确定马尔可夫链一步状态转移概率矩阵之后，按照最大概率准则对矩阵的行向量进行分析，即当max｛P，P，…，P｝＝P时，可以认为系统的状态下一步将转移到S，从而完成对系统状态的预测。

（4）计算预测值并进行修正。根据无偏灰色模型计算得出预测值，并结合步骤（3）中预测的系统状态对灰色预测值进行修正，最终得到无偏灰色-马尔科夫链预测模型的预测值。

3 牵引系统故障预测实例

3.1 无偏灰色模型预测

某地铁*号线*车型2014～2020年牵引系统受电弓模块的故障次数原始数据见表2。

表2 2014～2020年地铁牵引系统受电弓模块故障次数统计表Tab.2 The number of failures of the pantograph module of the subway traction system from 2014 to 2020

根据故障原始数据建立牵引系统受电弓模块无偏灰色预测模型，并进行精度检验和对2020年的故障次数进行预测。模型建立过程如下：

（1）构造牵引系统受电弓模块故障次数时间序列集：

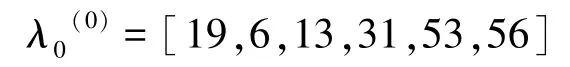
（2）求级比（）和可容覆盖区间：

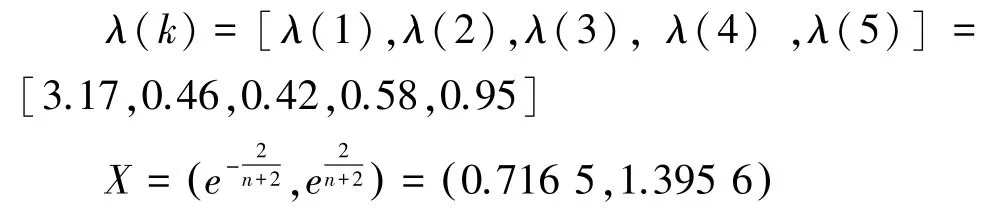
由于级比（）没有全部落在可容覆盖区间内，所以该时间序列集不满足灰色预测模型的要求，因此需对其作平移变换处理，使其满足以上要求。将原始数据序列（加上100，得到数据序列为：

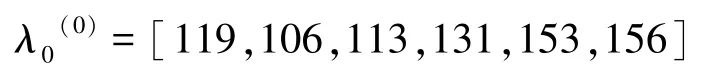
经过计算，该数据序列所有的级比（）均落在可容覆盖区间内，满足灰色预测模型的要求，故可以用来建模。

（3）计算累加矩阵和常数向量为：

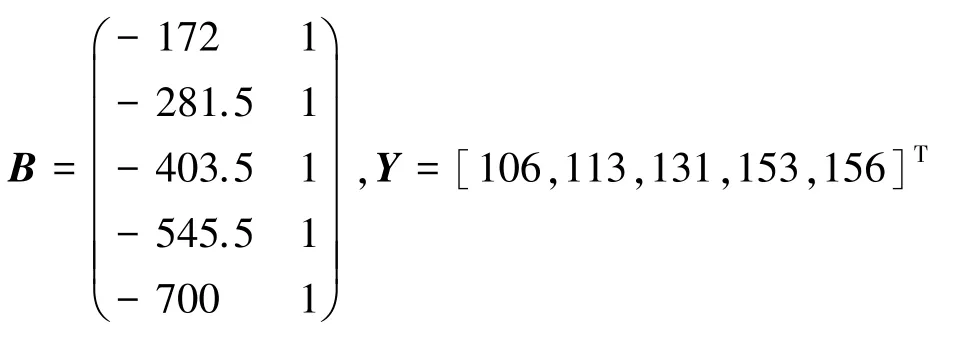
（4）利用Matlab软件计算相关参数，可得无偏灰色预测函数为：

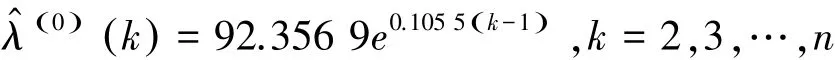
则数据序列的拟合值为：

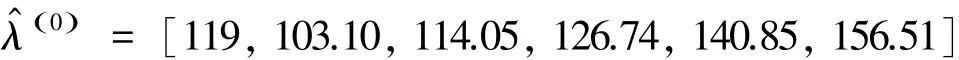
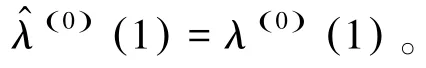
（5）将其还原便可得到原始数据的拟合值：

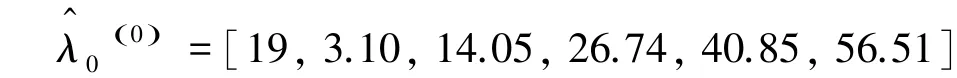
（6）拟合结果及误差分析。模型拟合结果及误差分析见表3。

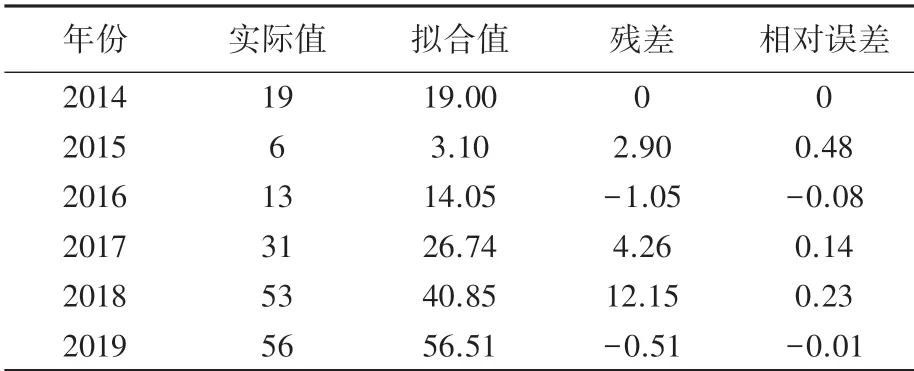
表3 无偏灰色模型拟合结果统计表Tab.3 Statistical table of unbiased grey model fitting results

（7）预测2020年故障次数。利用无偏灰色模型对2020年受电弓模块故障次数进行预测，最终预测结果为73.93，与实际故障次数79相比，相对误差为0.06，可以看出，无偏灰色预测模型的准确性较高。

3.2 无偏灰色-马尔可夫模型预测

以无偏灰色模型预测值为基础建立无偏灰色-马尔可夫模型，并进行误差分析和预测2020年故障次数，过程如下：

（1）比较2014～2019年牵引系统受电弓模块的故障次数无偏灰色拟合值与实际值，计算并分析相对误差，将相对误差分为4个区间，对应4种状态：状态1，［010，001）；状态2，［001，015）；状态3，［015，030）；状态4，［030，048］。计算各状态的中间值为：0045，008，0225，039。

（2）根据表中已经列出的相对误差，可以得出相应的状态。接着利用修正函数，可得马尔可夫链修正后的预测值。修正函数计算公式如下：

则马尔可夫模型预测值序列为：

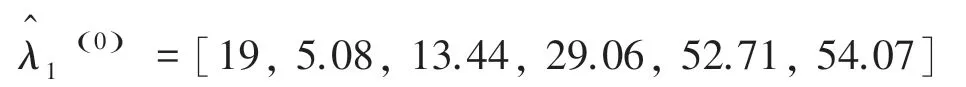
（3）误差分析。无偏灰色-马尔可夫模型的拟合结果与误差见表4。

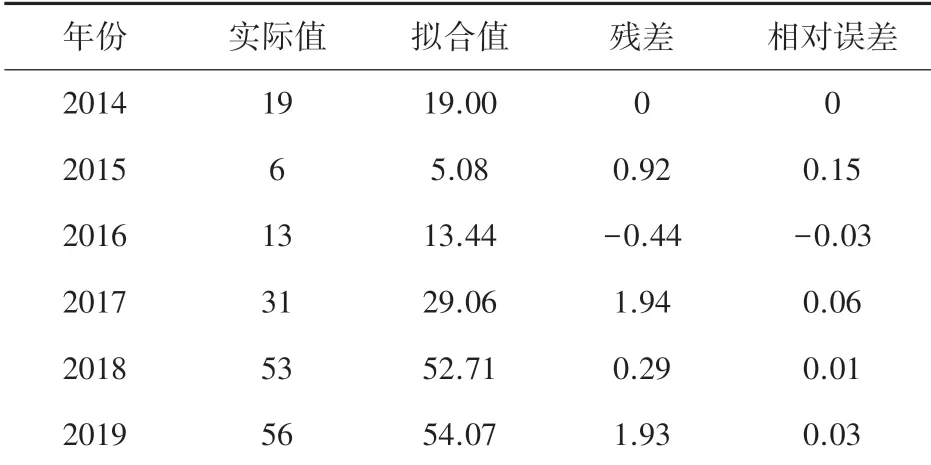
表4 无偏灰色-马尔可夫模型拟合结果统计表Tab.4 Statistical table of unbiased grey-Markov model fitting results

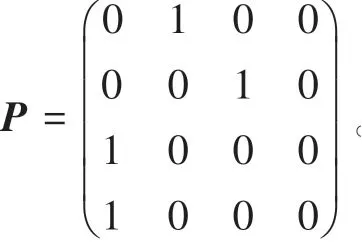
已知2020年受电弓模块无偏灰色故障预测次数为73.93，则利用修正函数可以计算出无偏灰色-马尔可夫模型的预测值为：

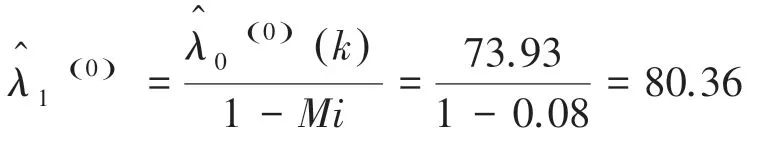
而2020年受电弓模块实际故障次数为79，相对误差为-0.02，预测结果的准确性较之前有了明显提升。

（6）模型精度检验。对2种模型的预测效果进行比较，见图1和表5。

表5 故障预测模型精度等级检验表Tab.5 Accuracy grade inspection table of failures prediction model

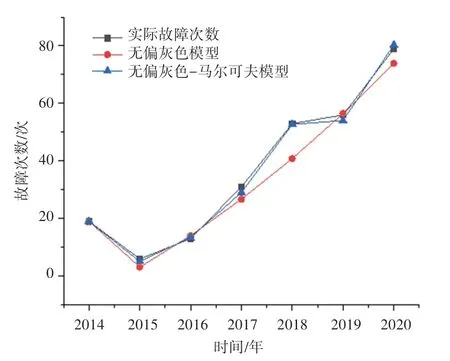
图1 2种模型的拟合结果、预测结果与实际故障次数的比较Fig.1 Comparison of fitting results，predicted results and actual failure times of the two models

根据图1可以看出，2种预测模型的拟合结果、预测结果与实际值的变化趋势较为符合，但无偏灰色-马尔可夫预测模型无论是拟合结果、还是预测结果都与实际值更加贴合，准确性更高。根据表5可以看出，无偏灰色模型的2项指标、分别达到了一级和二级标准，有一项指标达到了三级标准，因此可以认为无偏灰色模型的预测精度等级达到了一般及以上，而本文提出的无偏灰色-马尔可夫模型的三项指标都达到了一级标准。由此可见，相比于无偏灰色模型，无偏灰色-马尔可夫模型具有较高的预测精度，且精度等级为一级（精确）。

4 结束语

针对地铁牵引系统故障预测问题，本文以受电弓模块为例，在无偏灰色模型的基础上，结合马尔可夫模型来对其故障进行预测。模型精度检验结果表明：与单独采用无偏灰色预测模型相比，无偏灰色-马尔可夫模型的预测结果误差更小、预测精度也更高，可为地铁列车牵引系统的可靠性评估及状态检修提供依据，对于牵引系统主动维护策略的制定具有重要的应用价值。不足之处在于，在构建该预测模型的过程中，系统状态划分环节易受到主观人为因素的影响。因此，如何排除干扰因素，更加科学地处理原始数据和划分系统状态是下一步研究的重点。