中考中三角形面积问题的解决策略

龚辉

三角形的面积问题因变化多端、解法多样，经常出现在中考试卷上。三角形面积问题又经常与动点相结合，产生两大难点：一是导致了图形的不确定性，考查分类思想以及对动态图形的想象和处理能力;二是会引入参数，考查含参坐标或含参线段的运算。倘若三角形的底和高均含参数，则三角形面积的代数式会呈现二次函数关系，中考时常常可做进一步的研究，如最值问题、取值范围和定值问题等。下面选取中考试卷中的几道典型试题从三个角度进行剖析。

一、直接利用面积公式

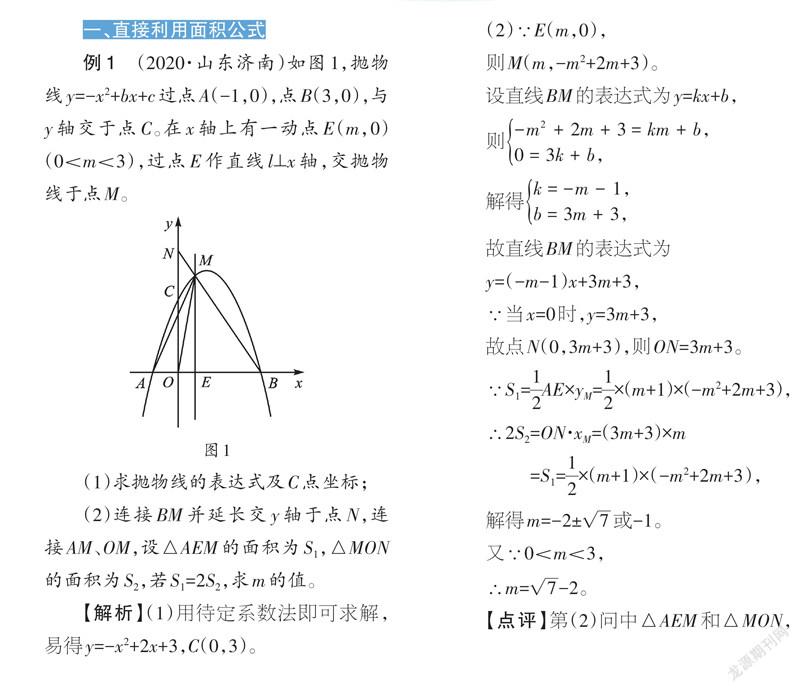
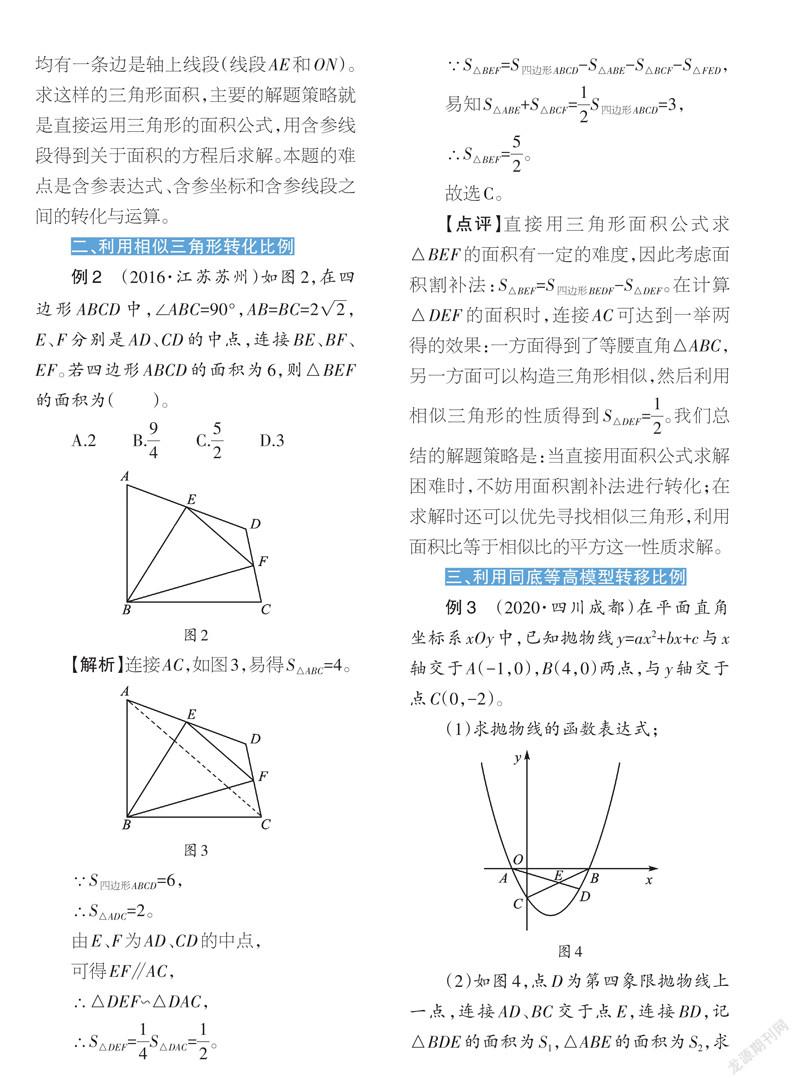
例1 （2020·山东济南）如图1，抛物线y=-x2+bx+c过点A（-1，0），点B（3，0），与y轴交于点C。在x轴上有一动点E（m，0）（0

（1）求抛物线的表达式及C点坐标;

（2）连接BM并延长交y轴于点N，连接AM、OM，设△AEM的面积为S1，△MON的面积为S2，若S1=2S2，求m的值。

【解析】（1）用待定系数法即可求解，易得y=-x2+2x+3，C（0，3）。

（2）∵E（m，0），

则M（m，-m2+2m+3）。

设直线BM的表达式为y=kx+b，

则[-m2+2m+3=km+b，0=3k+b，]

解得[k=-m-1，b=3m+3，]

故直线BM的表达式为

y=（-m-1）x+3m+3，

∵当x=0时，y=3m+3，

故点N（0，3m+3），则ON=3m+3。

∵S1=[12]AE×yM=[12]×（m+1）×（-m2+2m+3），

∴2S2=ON·xM=（3m+3）×m

=S1=[12]×（m+1）×（-m2+2m+3），

解得m=-2±[7]或-1。

又∵0

∴m=[7]-2。

【点评】第（2）问中△AEM和△MON，均有一条边是轴上线段（线段AE和ON）。求这样的三角形面积，主要的解题策略就是直接运用三角形的面积公式，用含参线段得到关于面积的方程后求解。本题的难点是含参表达式、含参坐标和含参线段之间的转化与运算。

二、利用相似三角形转化比例

例2 （2016·江苏苏州）如图2，在四边形ABCD中，∠ABC=90°，AB=BC=[22]，E、F分别是AD、CD的中点，连接BE、BF、EF。若四边形ABCD的面积为6，则△BEF的面积为（ ）。

A.2 B.[94] C.[52] D.3

【解析】连接AC，如图3，易得S△ABC=4。

∵S四边形ABCD=6，

∴S△ADC=2。

由E、F為AD、CD的中点，

可得EF∥AC，

∴△DEF∽△DAC，

∴S△DEF=[14]S△DAC=[12]。

∵S△BEF=S四边形ABCD-S△ABE-S△BCF-S△FED，

易知S△ABE+S△BCF=[12]S四边形ABCD=3，

∴S△BEF=[52]。

故选C。

【点评】直接用三角形面积公式求△BEF的面积有一定的难度，因此考虑面积割补法：S△BEF=S四边形BEDF-S△DEF。在计算△DEF的面积时，连接AC可达到一举两得的效果：一方面得到了等腰直角△ABC，另一方面可以构造三角形相似，然后利用相似三角形的性质得到S△DEF=[12]。我们总结的解题策略是：当直接用面积公式求解困难时，不妨用面积割补法进行转化;在求解时还可以优先寻找相似三角形，利用面积比等于相似比的平方这一性质求解。

三、利用同底等高模型转移比例

例3 （2020·四川成都）在平面直角坐标系xOy中，已知抛物线y=ax2+bx+c与x轴交于A（-1，0），B（4，0）两点，与y轴交于点C（0，-2）。

（1）求抛物线的函数表达式;

（2）如图4，点D为第四象限抛物线上一点，连接AD、BC交于点E，连接BD，记△BDE的面积为S1，△ABE的面积为S2，求[S1S2]的最大值。

【解析】（1）将A（-1，0），B（4，0），C（0，

-2）分别代入y=ax2+bx+c，得a=[12]，b=[-32]，c=-2，∴抛物线的函数表达式为y=[12]x2-[32]x-2。

（2）设直线BC的表达式为y=kx+n，将B（4，0），C（0，-2）代入，可得k=[12]，n=-2，∴直线BC的表达式为y=[12]x-2。

如图5，过点D作DG⊥x轴于点G，交BC于点F，过点A作AK⊥x轴，交BC的延长线于点K，∴AK∥DG，∴△DFE∽△AKE，

∴[DFAK]=[DEAE]，

∴[S1S2]=[S△BDES△ABE]=[DEAE]=[DFAK]。

∵xA=xk=-1，∴yk=[-52]，即AK=[52]。

设点D（m，[12]m2[-32]m-2），

则DF=[-12]m2+2m。

∴[S1S2]=[-15]m2[+45]m=[-15]（m-2）2[+45]。

∴当m=2时，[S1S2]有最大值，为[45]。

【点评】本题的第（2）问有两个难点：一是点D在抛物线上运动，需要引入参数，如D的坐标为（m，[12]m2[-32]m-2），DF=[-12]m2+2m等;二是两个三角形的面积比该如何计算？观察两个三角形在图形中的位置特征，可以发现这两个三角形有一条边是公共边（同高模型，可命名为“共边三角形”），如图6中AD为△ABD和△ACD的“共边”，关于面积的结论是[S△ABDS△ACD]=[BDCD]（如本题中的[S1S2]=[DEAE]），然后通过作高的方法将斜向线段改为轴向线段（即本题中[DEAE]=[DFAK]），方便与坐标建立联系，从而得到关于面积比的二次函数。

综上可知，中考关于面积的问题通常有三条解决途径可供选择，由于题目背景、图形类型、设问方法等变化较多，需要同学们在学习中不断整理、提炼和总结，形成行之有效的解题策略，从而在解题时游刃有余。