知错“究”改

刘立军

二次函数是初中数学的重要内容，也是各地中考中重点考查的知识点之一。但同学们在解有关二次函数问题时，常出现这样或那样的错误。为了帮助同学们在解题时减少失误，现对二次函数中一些常见的易错点进行剖析，以帮助同学们更好地理解和掌握二次函数。

一、概念理解不清

例1 已知关于x的函数y=（k-3）xk2-3k+2+kx+1是二次函数，则k= 。

【错解】根据二次函数的概念，令k2-3k+2=2，解得k=0或k=3。

【分析】根据二次函数的概念，要使y=（k-3）xk2-3k+2+kx+1是二次函数，k必须满足两个条件：①k2-3k+2=2;②k-3≠0。两者缺一不可。

【正解】根据二次函数的概念，得

[k2-3k+2=2，k-3≠0，]解得k=0。

二、函数性质掌握不牢

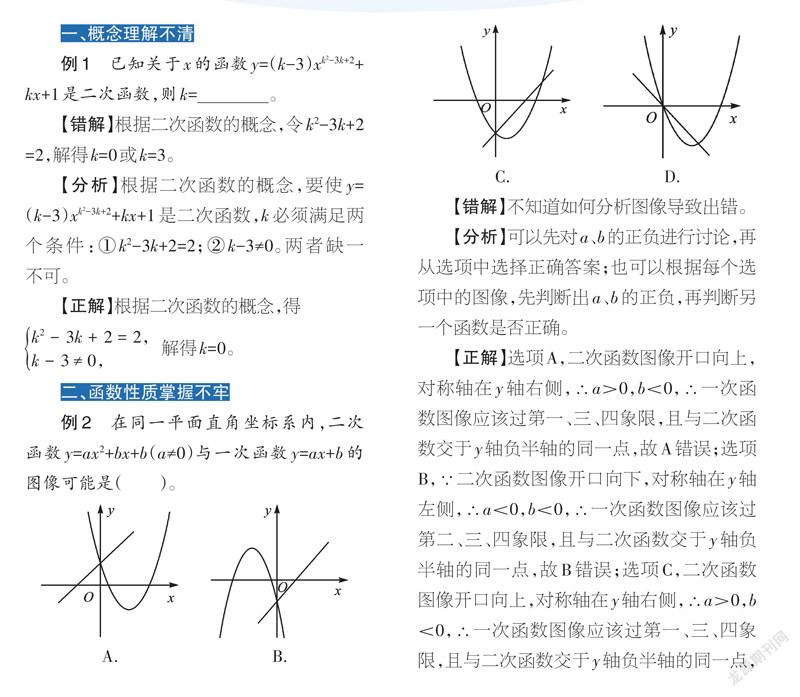
例2 在同一平面直角坐標系内，二次函数y=ax2+bx+b（a≠0）与一次函数y=ax+b的图像可能是（ ）。

【错解】不知道如何分析图像导致出错。

【分析】可以先对a、b的正负进行讨论，再从选项中选择正确答案;也可以根据每个选项中的图像，先判断出a、b的正负，再判断另一个函数是否正确。

【正解】选项A，二次函数图像开口向上，对称轴在y轴右侧，∴a>0，b<0，∴一次函数图像应该过第一、三、四象限，且与二次函数交于y轴负半轴的同一点，故A错误;选项B，∵二次函数图像开口向下，对称轴在y轴左侧，∴a<0，b<0，∴一次函数图像应该过第二、三、四象限，且与二次函数交于y轴负半轴的同一点，故B错误;选项C，二次函数图像开口向上，对称轴在y轴右侧，∴a>0，b<0，∴一次函数图像应该过第一、三、四象限，且与二次函数交于y轴负半轴的同一点，故C正确;选项D，二次函数图像开口向上且过原点，则a>0，b=0，∴一次函数图像应该过第一、三象限，且与二次函数交于原点，故D错误。故选C。

例3 若A（1，y1），B（3，y2），C（-3，y3）三点都在二次函数y=x2-4x-m的图像上，则y1，y2，y3的大小关系是 。

【错解】∵-3<1<3，∴y3

【分析】错解只考虑A，B，C三点横坐标之间的关系，而忽视了它们不在对称轴x=2的同侧。对于对称轴两侧的点，应根据它到对称轴的距离来比较函数值的大小。

【正解】函数对称轴为直线x=2，图像开口向上，在对称轴左侧，y随x的增大而减小，可判断y1

三、忽视隐含条件

例4 若二次函数y=mx2+4x+m-1的最小值是2，则m的值为 。

【错解】∵二次函数y=mx2+4x+m-1的最小值是2，∴[4ac-b24a]=[4m（m-1）-424m]=2，即m2-3m-4=0，解得m1=4，m2=-1。

【分析】二次函数有最小值，则开口向上，所以错解忽略了“m>0”这一隐含条件。

【正解】∵二次函数y=mx2+4x+m-1的最小值是2，∴[4ac-b24a]=[4m（m-1）-424m]=2，即m2-3m-4=0，解得m1=4，m2=-1。∵二次函数有最小值，∴函数图像开口向上，m>0，从而m=4。

四、缺乏数形结合思想

例5 已知二次函数y=（x+1）2-4，当-2≤x≤2时，求函数y的最小值和最大值。

【错解】当x=-2时，y=-3，当x=2时，y=5，∴当-2≤x≤2时，函数的最小值是-3，最大值是5。

【分析】错解误以为端点的值就是这段函数的最值。解决此类问题，可以画出函数图像，借助图像的直观性帮助理解。

【正解】二次函数y=（x+1）2-4的对称轴为直线x=-1，开口向上，∴当x>-1时，y随x的增大而增大，当x<-1时，y随x的增大而减小。由图像可知：在-2≤x≤2内，当x=2时，y有最大值，y=（2+1）2-4=5;当x=-1时，y有最小值-4。

五、忽视分类讨论思想

例6 若函数y=（a-1）x2-4x+2a的图像与x轴有且只有一个交点，则a的值为 。

【错解】由题意，可知Δ=16-8a（a-1）=0，解得a=2或a=-1。

【分析】错解只考虑了a≠1，即函数图像是抛物线的情形。但题目并没有明确指出函数是二次函数。当a=1时，此函数为一次函数y=-4x+2，与x轴永远会有一个交点，因此出现了漏解的情况。

【正解】①当函数为一次函数时，a-1=0，解得a=1;②当函数是二次函数时，可得Δ=16-8a（a-1）=0，解得a=2或a=-1。

综上所述，a的值为1或-1或2。