函数型部分线性模型的参数估计及其变量选择
袁晓惠,曹儒雅,金宛霖
(长春工业大学 数学与统计学院,吉林 长春 130012)
0 引言
函数型数据最初是由J.Ramsay[1]提出的,是一种无限维的数据.函数型数据是指在紧区域上的实值函数的一个实现[2].由离散数据拟合得到光滑曲线是函数型数据的研究对象[3].由于函数型数据的无限维属性,使得以往的多元统计方法不再适用,这为函数型数据的发展提供了先决条件.此外,由于函数型数据是无穷维的,在现实中有一些数据是不能完全被观测到的,只能观测到其有限的离散时间点.因此可将函数型数据根据数量大小分为稠密数据和稀疏数据,根据取值形式分为均衡数据和非均衡数据.根据样本观测量的大小及分析函数型数据的工具的不同,可将研究函数型数据的学者分为三个学派,即经典学派、随机学派和法国学派.
近年来,关于函数型数据分析已经积累了大量的成果.常用的函数型数据分析的工具是函数型线性模型,主要有两种:一是标量型响应变量的函数型线性模型,二是函数型响应变量的函数型线性模型.本文只考虑响应变量为标量型的函数型回归模型,再根据协变量的数据类型,可以将函数型回归模型分为两类:协变量为函数型数据的回归模型和协变量为函数型与标量型混合数据的回归模型.
比较经典的协变量为函数型数据的函数型回归模型是函数型线性模型.该模型是研究最早和最广泛的模型之一.H.Cardot[4]首次研究了该模型的计算问题,并于2003年基于样条基底展开和主成分降维的估计,推导了基于样条展开估计的渐近收敛性质;T.T.Cai等[5]在理论上推导了函数线性模型预测的收敛速度,在一定条件下,得出了预测能达到参数收敛速率的结论;H.G.Muller等[6]研究了基于主成分得分的函数加性模型的估计和理论性质;F.Yao等[7]研究了函数型数据二次回归模型;在再生核希尔伯持空间上,M.Yuan等[8]提出惩罚估计相对于主成分回归能在较弱的条件下达到最优收敛速率;T.T.Cai等[9]在再生核希尔伯特空间里研究了预测的最优收效速率和自适应性;Z.Lin等[10]利用最小二乘基于样条技术进行了函数型回归模型的局部稀疏估计;Q.Wang等[11]提出了基于函数充分性降维基底来估计函数的线性模型,并推导了相关理论性质.
比较经典的协变量为混合数据的函数型回归模型是函数型部分线性模型.此模型由D.Zhang等[12]提出;H.Shin[13]主要研究的是模型基于函数型主成分的估计问题,并得到了参数部分的渐进正态性和函数系数的收敛速度;H.Shin等[14]使用基于FPCA 的最小二乘方法和岭回归方法研究了该模型的估计和预测,并证明了在一定的条件下斜率函数的估计能达到最优收敛速度;丁辉[15]对函数型部分线性单指标模型、函数型部分线性回归模型等几类函数型回归模型的估计与预测展开了研究.
在实际应用中,遇到的协变量大部分是多维的,而在这些协变量中有一些是无关变量,变量选择是剔除无关变量的一个很好的工具.常用的变量选择方法有岭回归、Lasso、SCAD等.Lasso变量选择方法的优点是,它既改进了传统变量选择方法在模型选择方面的不足之处,同时又保留了一些优良的性质[16].此外,岭回归和 Lasso 回归方法也可以消除自变量间存在的共线性问题[17],同时具有一定的稳定性[18].SCAD方法则改进了Lasso方法在模型应用上的一些局限.在函数型部分线性模型中,也可采用适当的变量选择方法,剔除无关变量.
本文的估计方法和结论不仅丰富了函数型回归模型的研究,给函数型回归模型的发展提供了更多的参考,更将有助于以后在经济学、医学、生物学等领域的发展与探索.
1 函数型部分线性模型的估计方法
1.1 参数估计
函数型部分线性模型是研究函数型数据的一个应用较为广泛的模型[12],形式为
(1)
其中:Yi为响应变量;X1(t),X2(t),…,Xn(t)是定义在区间[0,T]上的函数型协变量;Zi=(Zi1,…,Zip)T为p维协向量;β(t)为斜率函数;α=(α1,…,αp)T为Zi的系数;εi为误差项,且εi~N(0,σ2).此模型即描述了标量型响应变量和函数型与标量型的混合协变量之间的关系.

用B样条方法表示β(t),即
其中:B(t)=(B1(t),B2(t),…,BM+d(t))T是B样条基函数;b=(b1,b2,…,bM+d)T是相应的系数.但是当M较大时,直接使用B样条方法近似,会使得估计值产生较大的波动性,因此,在目标函数中加入粗糙度惩罚函数,即
(2)
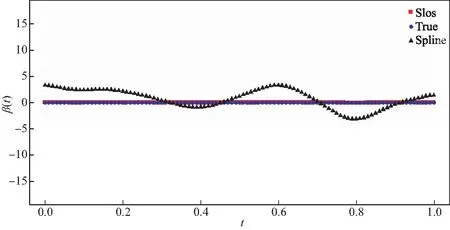
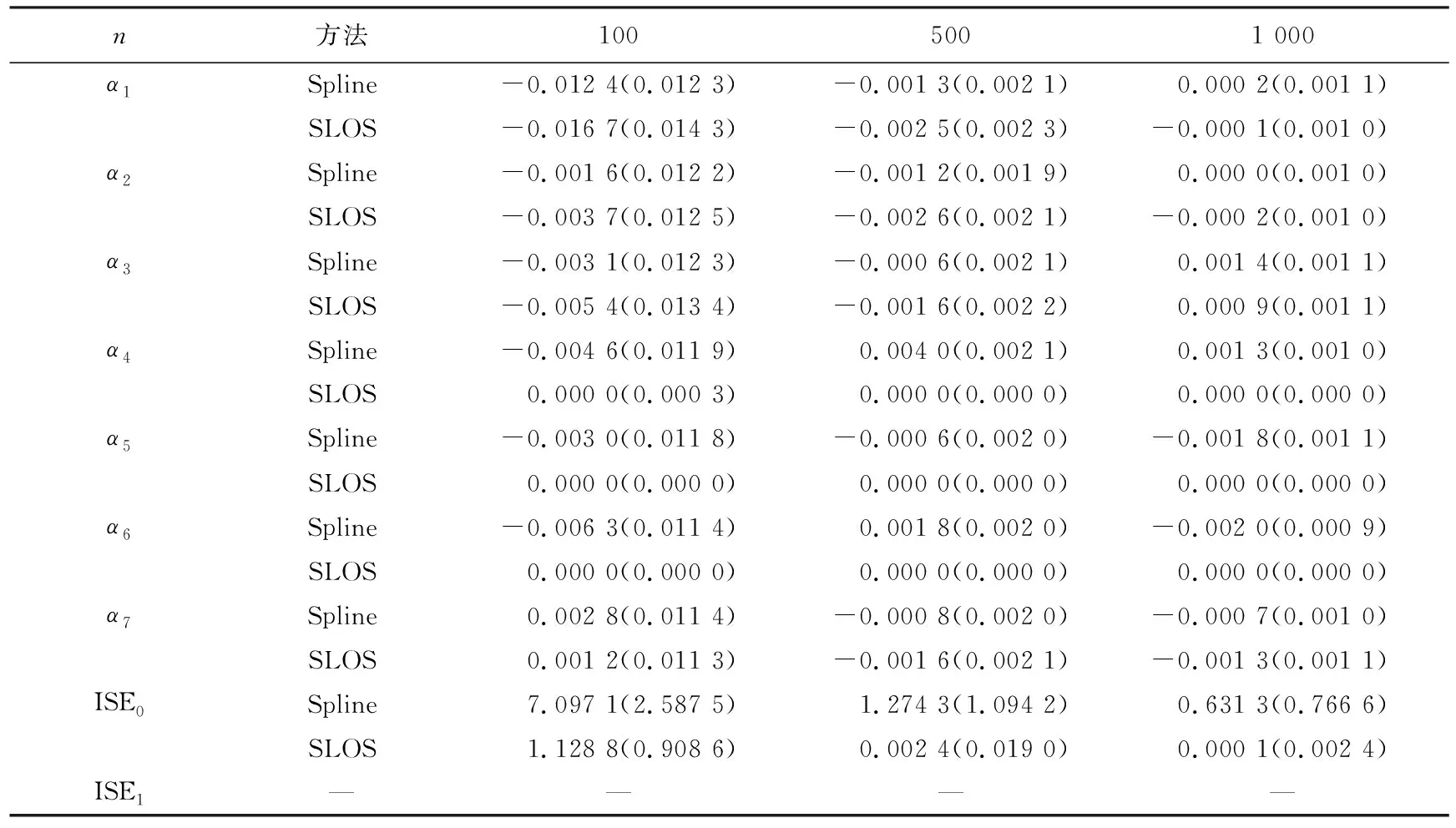
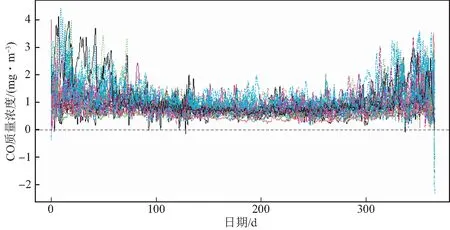
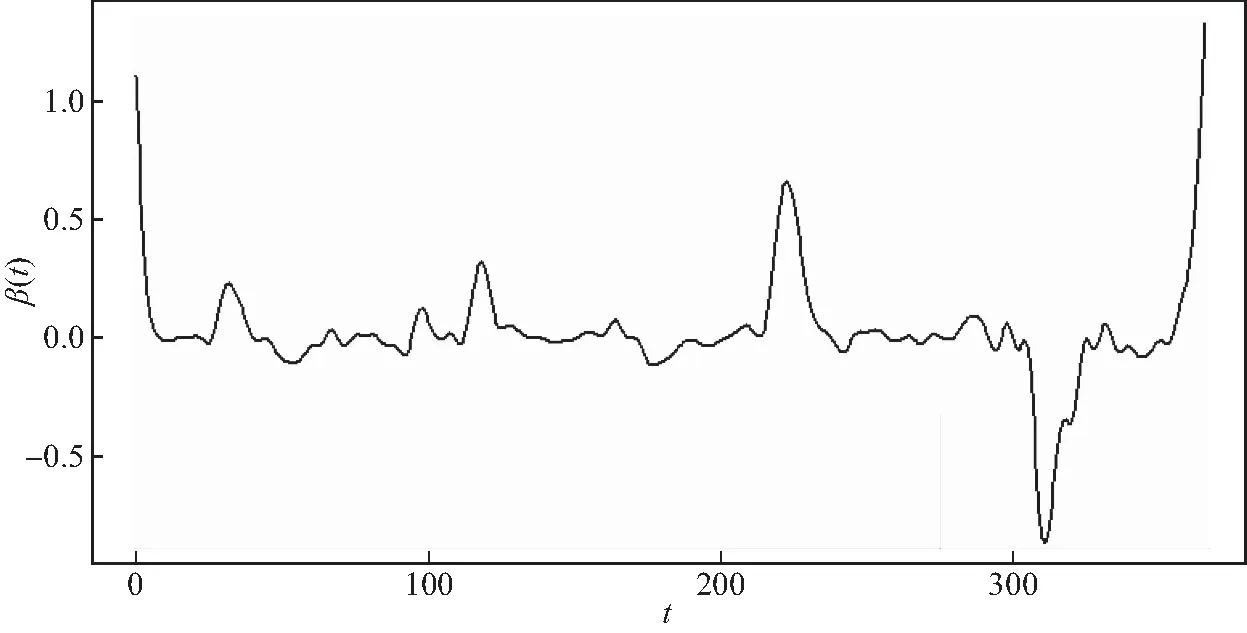
其中Dmβ为β(t)的m阶导数,且m 此外,当M较大时,可以通过加入光滑消边绝对偏离(SCAD)惩罚函数pλ1(u)来实现斜率函数空子区间的寻找,同时加入光滑消边绝对偏离(SCAD)惩罚函数对α中零分量的寻找.即最小化下面的目标函数: 其中 通过最小化上面的目标函数,可以实现斜率函数空子区间与非空子区间的寻找和标量型系数零分量的识别.为了计算方便,引入一些符号,令 令 Y=(Y1,…,Yn)T,Z=(Z1,…,Zn)T,X(t)=(X1(t),…,Xn(t))T, U=(uij)n×(M+d),V=(vij)(M+d)×(M+d),G=(U,Z),g=(b,α). 由此可得 计算得到 目标函数的第二项可转化为γ‖Dmβ‖2=γbTVb.为了方便计算目标函数的第三项,利用文献[10]中的定理1,fSCAD惩罚项可被近似为 利用LQA方法来计算,即 其中: 但由于H(β(0))不依赖于β,因此对目标函数没有影响,即可写为 目标函数第四项中的pλ2(|αj|)可以进行泰勒展开,即 (3) 对式(3)求一阶导,有 求二阶导,有 令 =(GTG+nSS)-1GTY. 为了更清楚地表达上述估计思想,列出如下估计步骤: 为了实现上述估计,需要进行调节参数的选择.经过多次研究分析,γ=1e-7时效果最好.下面进行λ1,λ2的选择. GCV准则定义为 其中e(λ1)=tr[PG{(λ1)}],PG{(λ1)}=GGT. BIC准则定义为 (Xi(t),Zi,Yi)由如下模型产生: 第一种β(t)=0,即只存在空子区间. β(t)估计值的表现通过积分平方误(ISE)来评价,即 其中l0和l1表示空子区间和非空子区间的长度,N(β)和S(β)则表示对应的空子区间和非空子区间.α估计值的表现则通过偏差和均方误差来体现.模拟均重复1 000次. 第一种斜率函数的结果如图1所示. 图1 情形1中β(t)的真实曲线图及其估计曲线 由此可见,当斜率函数为零时,Spline方法可使得估计值在零附近上下波动,而SLOS方法可使斜率函数的估计完全变为零.因此,在只存在空子区间的情况下,SLOS方法比Spline方法效果更好.具体分析结果如表1所示: 表1 情形1估计的偏差和(均方误差)或ISE0、ISE1和(标准差) 由表1可分析得,SLOS方法的ISE0比Spline方法的ISE0要小很多,这表明SLOS可以使斜率函数完全被惩罚为零.而对α的估计方面,SLOS方法能够更好的识别零向量,Spline方法则不能达到这样的效果.因此,总体而言,SLOS方法要优于Spline方法. 第二种斜率函数的结果如图2所示. 图2 情形2中β(t)的真实曲线图及其估计曲线 由此可见,当斜率函数同时存在空子区间与非空子区间的时候,SLOS方法可以很好的识别空子区间,使其被估计为零.与Z.Lin[10]结论一致.具体分析结果如表2所示. 表2 情形2估计的偏差和(均方误差)或ISE0、ISE1和(标准差) 由表2可分析得,SLOS方法的ISE0比Spline方法的ISE0要小很多,即SLOS方法可以很好的识别空子区间.而随着样本量的增加,两种方法的ISE1之间的差值逐渐减小.而对α的估计方面,SLOS方法能够更好地识别零向量,因此整体上,SLOS方法要比Spline方法更加适用于此模型. 第三种斜率函数的结果如图3所示. 图3 情形3中β(t)的真实曲线图及其估计曲线 由此可见,当斜率函数不为零,即只存在非空子区间时,Spline方法的估计曲线与真值曲线趋于一致,明显优于SLOS方法.因此,在这种情况下,SCAD惩罚函数将不再适用.具体分析结果如表3所示. 由表3可分析得,Spline方法的ISE1比SLOS方法的ISE1要小很多,即在只存在非空子区间的情况下,Spline方法更加适用.在α的估计方面,SLOS方法的效果更好.这表明,SLOS方法更加适用于存在空子区间或者零向量的情况,而只有非空子区间或者非零向量的情况下,Spline方法则更优越. 表3 情形3估计的偏差和(均方误差)或ISE0,ISE1和(标准差) 本节将利用本文中所述的模型和方法对2018年中国主要的31个城市的空气质量进行研究分析,该数据来源于https://quotsoft.net/air/以及中国统计年鉴.空气质量数据是由31个城市样本组成,其中每个样本包括PM2.5(μg/m3)含量,CO(mg/m3)含量,气温(℃),湿度(%),降水量(mm),日照时数(h),工业废水排放量(t),工业SO2(t)排放量,工业氨氮排放量(t).其中CO含量是由一年中每天24 h滑动均值构成的.首先对降水量、日照时数、工业废水排放量、工业SO2排放量和工业氨氮排放量等数据进行标准化,拟合的模型为 其中:Y是PM2.5含量;X(t)是CO含量;Z是气温、湿度、降水量、日照时数、工业废水排放量、工业SO2排放量和工业氨氮排放量.CO含量见图4. 由图4分析可得,在4月份到9月份之间空气中CO含量相对稳定,而在1—2月和11—12月之间CO含量则几乎两倍于4—9月份.这可以给环保部门在进行措施制定时提供一些依据.此外,β(t)估计值如图5所示. 图4 中国一年31个城市日均CO质量浓度 由图5分析可知,β(t)值整体波动趋于零,而在前端和后端有较大起伏,即在一年中秋冬季节CO含量对PM2.5含量有较大影响,此外,空气中CO含量对PM2.5含量的影响处于一个相对稳定的区间内. 图5 β(t)的估计曲线 得到α估计值如表4所示. 表4 α的估计值 由表4分析可知,降水量对于PM2.5含量呈负相关,即降水量越多,PM2.5含量越少,而日照时数、工业废水排放量和工业SO2排放量对于PM2.5含量的影响则呈正相关性.气温、湿度与工业氨氮排放量则相对没有影响. 以上信息不仅对相关部门、工厂、居民等在日常生活中有针对性、目的性、计划性和科学性地减少污气、废水排放,节能环保,废物利用,降低PM2.5含量等起到决定性作用,也更有助于今后的研究. 本文基于最小二乘和光滑样条法,加入光滑消边绝对偏离惩罚函数(SCAD)实现空子区间的寻找,再对标量型系数进行变量选择,得到斜率函数的局部稀疏估计和标量型系数中零分量的识别.在统计模拟部分,所提出的估计方法展现出良好的有限样本表现.最后的实证部分,通过对2018年中国主要的31个城市的空气质量进行研究分析,再次论证了本文所述估计方法的优良性与适用性. 此外,局部稀疏估计方法适用于很多的函数型回归模型,而本文只研究了函数型部分线性模型.所以,局部稀疏估计方法在其他的函数型回归模型中的应用是未来的一个研究方向.同时,只研究了一个函数型协变量的情况和有限维的标量型协变量的情况,而大多数情况下,函数型协变量和标量型协变量的维数很高,甚至是无限维的.因此,高维的函数型部分线性模型的局部稀疏估计与变量选择相结合是未来的又一个研究方向.
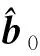
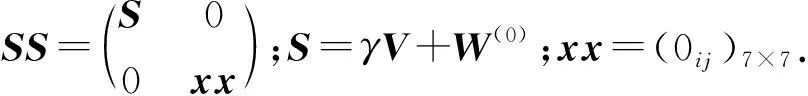
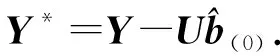
1.2 算法步骤
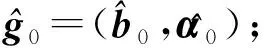
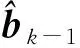
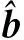
1.3 调节参数选择
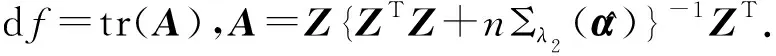
2 模拟分析
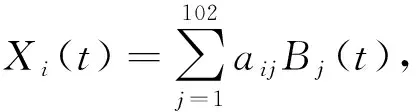
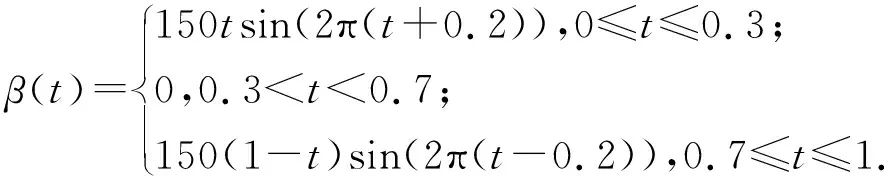
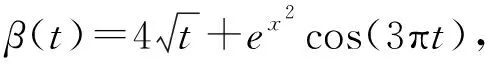
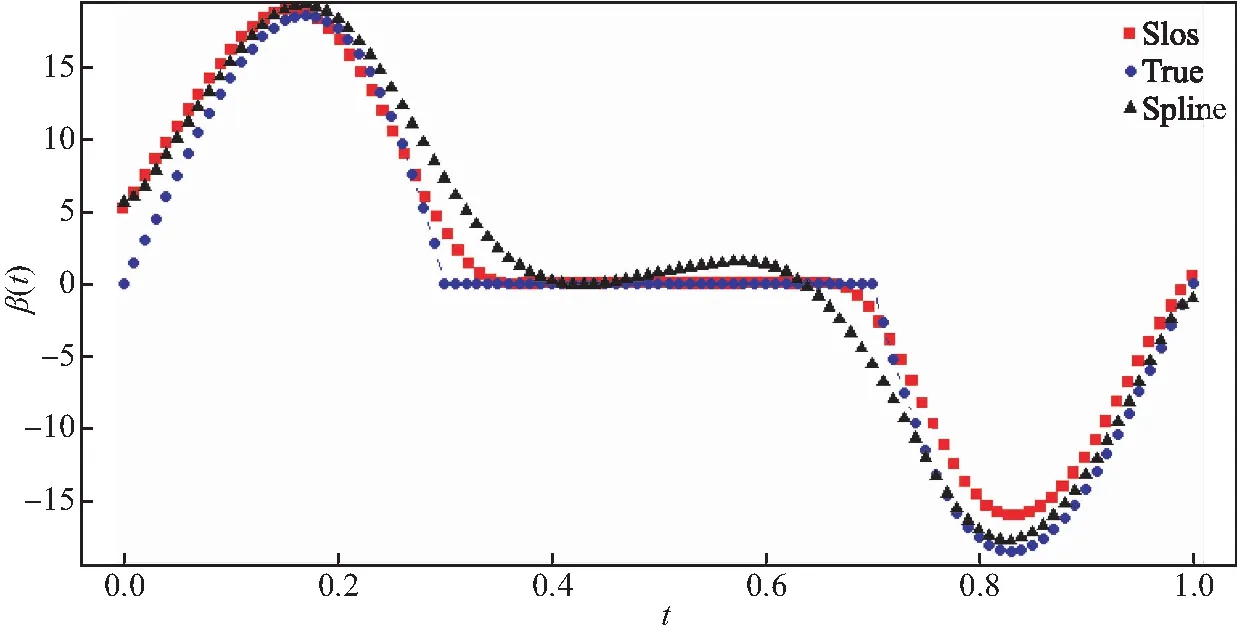
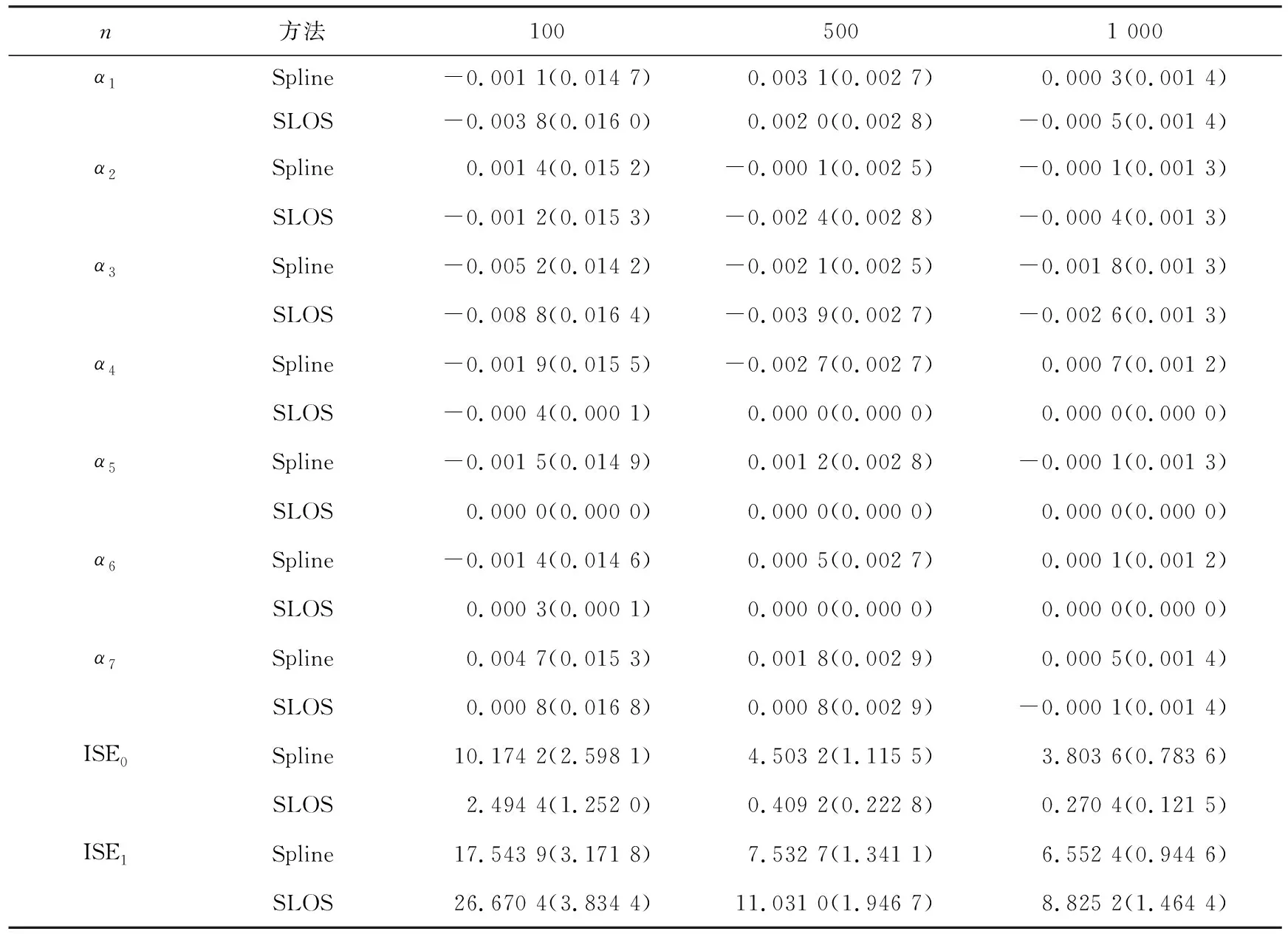
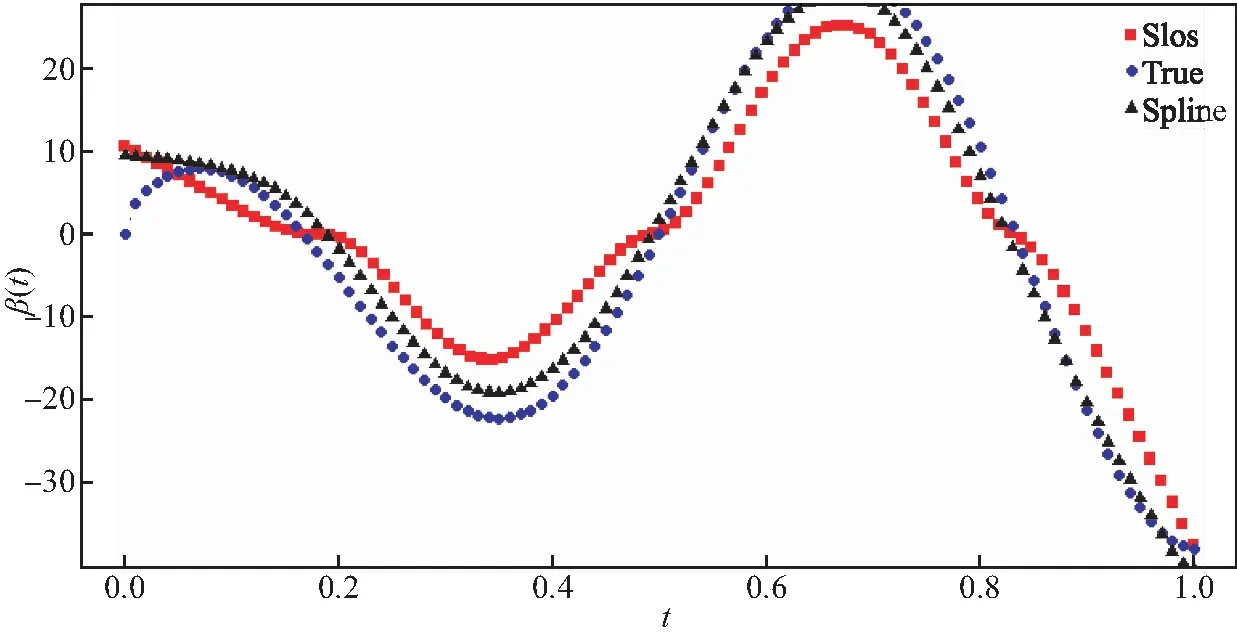
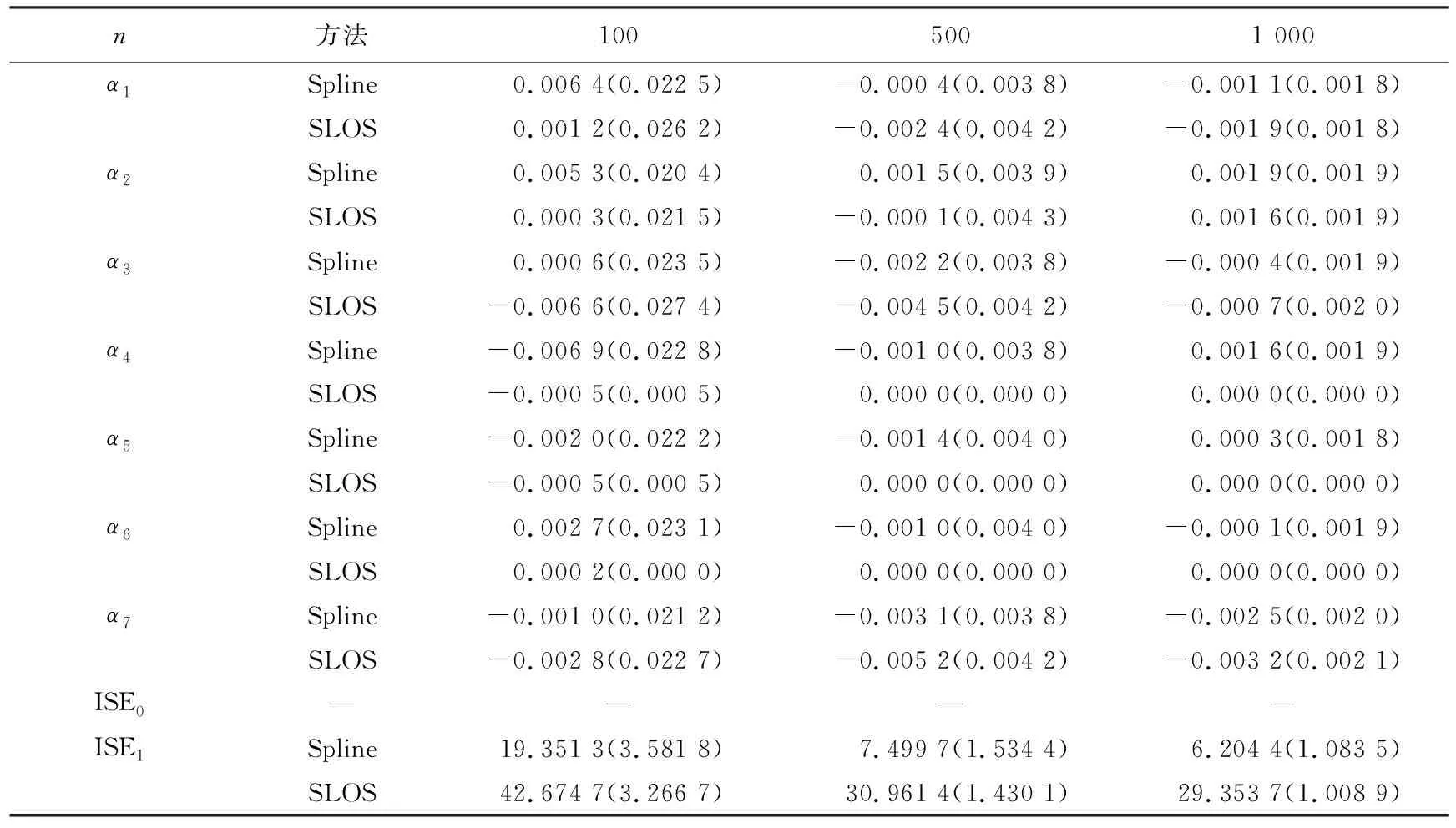
3 实例分析
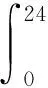

4 结语

