生物基1，3-丙二醇连续发酵过程的稳态分析与反馈控制

潘多涛，王旭东，史洪岩，修志龙

（1 沈阳化工大学信息工程学院，辽宁省化工过程控制技术重点实验室，辽宁沈阳 110142； 2 大连理工大学生物工程学院，辽宁 大连 116024； 3 浙江工业大学药学院，浙江杭州 310014）

引 言

1,3-丙二醇（PDO）是一种重要的化学品，广泛应用于化妆品及表面活性剂等，尤其是可用于合成可生物降解材料，如：聚对苯二甲酸丙二酯（PTT）、聚三亚甲基醚乙二醇和杂环化合物等[1]。目前，PDO可以通过化学合成或微生物发酵生产。化学合成过程中存在的高温高压、高毒性试剂以及昂贵的催化剂等问题严重制约了PDO 的工业化生产。相比之下，以微生物发酵是一种更加温和、低耗能、低成本以及更加环保的生产方式[2-3]。在可产PDO 的微生物中，肺炎克雷伯氏杆菌（Klebsiella pneumoniae）和丁酸梭菌（Clostridium butyricum）因具有较强的底物耐受性、较高转化率等优势而备受关注[4-5]。然而，发酵过程中产物（包括副产物）的毒性和反馈抑制等均会影响微生物的生长和PDO 的产出，这导致最终PDO 含量相对较低，不利于产品质量的提高和生产规模的扩大[6-7]。由于底物、产物和其他因素之间的关系较为错综复杂，依靠常规实验方法很难去深入探究背后的机理。相比之下，采用动力学建模对发酵系统进行机理分析是一种更高效的研究手段，可对目标过程进行有效预测及优化，为实际生产过程提供理论指导[8-10]。

自从Zeng 等[11]提出动力学模型来描述C.butyricum和K.pneumoniae的生长过程后，多种动力学模型被用来描述对应菌株的底物和能量消耗、产物形成以及其他因素的影响关系[12-13]。进一步地，利用数学模型优化K. pneumoniae发酵甘油生产PDO方面已经有不少的研究工作[14-19]，如：Wang 等[20]基于调整结构的模型，分析了甘油发酵过程的振荡特性，利用Hopf 奇点约束优化了操作条件；Zhu 等[16]、Kaur 等[21]分别利用动力学模型研究C. butyricum和Clostridium diolis的最佳培养条件，并优化营养底物补料策略以获得较高产量。除此之外，Ye 等[22]、Yang 等[23]利用混杂系统描述批式流加过程，研究了优化控制算法。然而，这些工作主要集中在对模型的分析和潜力的挖掘上，对发酵过程的自动化控制理论方面的研究仍然比较缺乏。而在流程工业智能自动化的背景下，PDO 生物发酵过程的自动化控制显得尤为重要[9,24-25]。

基于此，本文以K.pneumoniae连续发酵甘油生产1,3-丙二醇过程为研究对象，首先对发酵体系的多稳态特性进行考察，分析连续发酵的稳定性；在此基础上，设计了一种新型的发酵稀释率反馈控制系统，以期为PDO 自动化生产奠定一定的理论基础。

1 方 法

1.1 模型的来源

K. pneumoniae连续发酵模型源于前期研究[17]。该模型主要描述了甘油发酵转化为PDO 的动力学过程，包括主要代谢物的合成与分解之间的关系，对应的数学描述如下：

其中，X为生物量，g·L-1；D为稀释速率，h-1；CS0、CS分别为发酵过程中甘油的初始浓度和实时浓度，mmol·L-1；qS为 甘 油 的 比 消 耗 速 率，mmol·g-1·h-1；CPi为细胞外主要产物PDO、乙醇和乙酸的浓度，mmol·L-1；qi为上述三种胞外产物的比生成速率，mmol·g-1·h-1。模型中的参数列于表1[15]。

1.2 稳态分析

微生物发酵过程中影响稳态的因素可通过模型中特定参数的变化反映出来[26]。参数变化导致的系统状态发生跃迁的现象称为分支[27]，稳态解的分支与平衡的稳定性密切相关[28]。通过分支分析，能够分析非线性系统中参数对状态稳定性的影响。本文采用函数连续性分析工具[29]进行模型多稳态分析。

1.3 控制策略

在已报道的模型分析研究中，连续发酵过程的稀释速率通常取固定值[15,20]。稀释速率较高时，底物甘油流加速率较高，反应器中残余甘油量相对较多，这会导致大量残余甘油以等速率流出发酵罐，不但造成极大的浪费，还会影响后续产物的分离过程；而稀释速率较低时，甘油在发酵罐中的驻留时间增大，这能够使甘油得到比较充分的转化，但总体的生产强度较低。可见，稀释速率对生产性能和底物利用率有较大影响。因此，在现有模型[式(1)]的基础上，增加对稀释速率D的反馈控制，如式(2)所示。

式中，D0为基准参考稀释速率，h-1；β为稀释速率的调节增益系数；CeS为期望的残余甘油浓度，mmol·L-1；CePDO为期望的产物PDO 浓度，mmol·L-1；为期望的产物乙醇浓度，mmol·L-1；w1和w2为稀释速率调节项的权重占比；T是单位时间，取固定值1 h。

式(2)中的调节项会根据发酵系统中残余甘油或产物浓度的高低来反馈动态调整稀释速率D：残余甘油CS的增加会负向调节D（减少甘油的流加量），而产物浓度CPDO和CEtOH的增加则会正向调节D。

2 结果与讨论

2.1 发酵过程的稳态分析

在先前的研究中，发现K.pneumoniae的连续发酵过程具有强非线性特性，存在多稳态现象[17,30]，而且，在相同的操作条件下存在两种不同的稳定状态，这种现象不仅与操作条件有关，而且与操作模式有关。例如，在较高稀释率和较高底物浓度的条件下，底物浓度从低变高或由高到低减小将导致多稳态现象的出现。这种多稳态现象不但在实验中能够观察到[31-32]，而且还可通过对模型式(1)的连续性分析得到印证。因此，在前期工作基础上，进一步通过双因素分支分析探究多稳态发生的临界区域，结果见图1。

图1(a)～(e)中的点线、虚线和点划线分别表示稀释速率D取0.035、0.1 和0.26 h-1时反应物在不同初始甘油浓度下的稳态值变化趋势。同时，图中给出了D取0.1 h-1时不同初始甘油浓度下的反应物浓度实验值[图1(a)～(e)中三角形标记]。图中圆形标记表示出现多稳态时的极限分支点（limit point），任取其中一个极限点进行稀释速率和初始甘油浓度双因素的分支分析，会得到一个闭合曲线[图1(a)～(e)中实线]，该闭环会穿过不同稀释率下获得的各个极限点，参数的正向和负向变化结果交汇于尖点分支[cusp point，图1(a)～(e)中方形标记]，尖点是状态变化曲线中的一种奇异点，曲线上的点在移动到尖点时将会朝相反的方向移动。

图1(a)～(e)的结果显示，在特定的稀释速率下（如D= 0.1 h-1），稳态曲线都会经过两个极限分支点，两个极限点之间的区域不稳定，而两个极限点之外的区域稳定，表现为典型的双稳现象（bistable）[33]。此外，当稀释速率逐步增大时，稳态的不稳定区域会渐渐收缩，伴随着的是两个极限点会逐渐重合为一个并与尖点重合，最终多稳态现象会消失（如D=0.26 h-1）；反之，稀释速率的减小同样会使不稳定性区域收窄（如D=0.035 h-1）。总体上讲，在初期随着连续补料中甘油浓度的提高，生物量和（副）产物浓度均明显上升，直至底物甘油过量[如图1(c)中的拐点附近]。当甘油浓度持续增加时，残余甘油会迅速上升，此时生物量和乙酸浓度快速降低，相较而言PDO 和乙醇的浓度则相对缓慢地减小，直至接近0（过量的底物完全抑制了反应）。

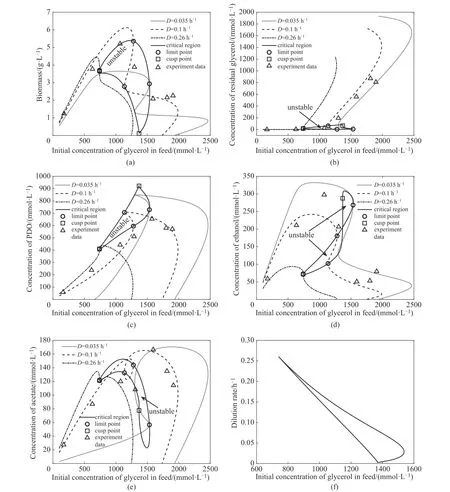
图1 发酵过程中不同稀释速率下的多稳态现象及其临界区域Fig.1 Multistability phenomenon and its critical region at different dilution rates during fermentation

生物代谢过程中的多稳态现象在大肠杆菌和酵母中均有一些报道[34-36]，其中底物抑制是其中的重要因素[37-38]。因此，推测K. pneumoniae的多稳态现象也与底物抑制[式(1)中的比生长速率]有关，可能原因是甘油作为单一底物在低浓度时扮演酶激活剂的角色，而在高浓度时则可能抑制酶促反应。当体系中的底物浓度从低到高时，细胞内的酶就会被激活从而激励产物的生成，而随着底物的进一步提高，则会超过酶的耐受阈值转而成为抑制剂，此时酶促反应会被抑制，残余底物浓度会提高而产物则会相应降低；另一方面，若底物浓度从高到低，胞内酶会被抑制较长一段时间，酶的活性较低，因此底物的消耗和产物的形成较少[17,30,32]。由于多稳态现象会对生产产生不利影响，在实际发酵过程中，工作点的选取应尽量避开多稳态的临界区域[20]。

2.2 发酵过程的优化控制

发酵生产水平不仅取决于生产菌种自身的性能，而且还受限于发酵条件和工艺等因素。本文采用的数学模型已经过大量研究验证了其可靠性，并在先前的工作中利用集成建模（ensemble modeling）方法进行了发酵过程的操作条件优化，获得了最优的初始甘油浓度和稀释速率[15]。然而，在以往的实验或模拟计算中，通常选取一个恒定的稀释速率进行研究分析，具有一定的局限性。本文在前述多稳态分析的基础上，考虑了底物甘油和产物PDO 的反馈控制策略，使得实际的稀释速率可随底物和产物的浓度动态调整。根据图1(f)中稀释速率和初始甘油浓度的临界区域（避开多稳态区域），并结合前期工作[15]中集成建模优化结果，设定初始甘油浓度CS0=780 mmol·L-1；在建立的稀释速率反馈控制方程[式(2)]中，基准稀释速率D0取0.23 h-1；期望的PDO稳态浓度为CePDO=421 mmol·L-1，期望的残余甘油浓度 为CeS= 25 mmol·L-1，期 望 的 乙 醇 稳 态 浓 度 为= 50 mmol·L-1；甘油调节项的权重w1取0.1，PDO调节项的权重w2取0.8，而稀释速率的调节增益系数β取0.15。经控制的优化计算结果如图2、表2所示。

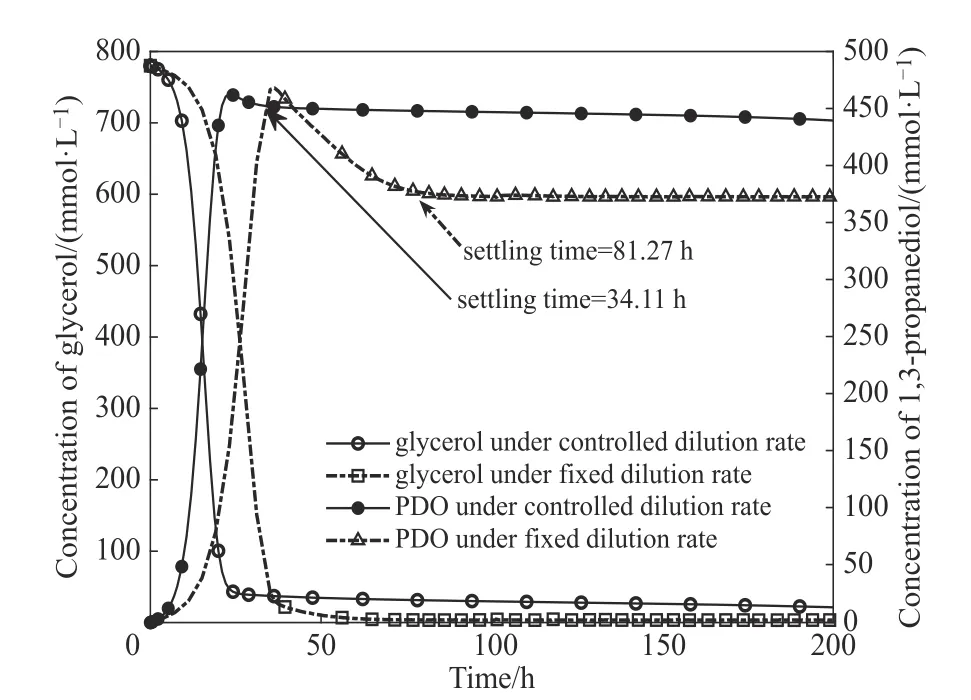
图2 不同稀释速率策略下的模拟结果对比Fig.2 Comparison of simulation results under different strategies for dilution rate

从表2 中的稳态数据可以看出，产物PDO 的浓度提高了约20%，这大大提高了甘油的转化率（由原来的0.478 mmol·mmol-1提高至0.563 mmol·mmol-1）；相对而言，残余甘油的浓度反而提高，仔细分析稳态数据可以发现，在未控制稀释速率的情况下，虽然甘油的残余量较低，但对产物PDO 生成的贡献是有限的，有相当比例的甘油转化为乙醇和乙酸。在施加控制手段后，代谢过程向有利于主产物形成的方向推进，稳态情况下乙醇的浓度下降超过30%，乙酸的浓度也有小幅下降。综合来看，在以恒定稀释速率培养时，发酵过程的生产强度为85.70 mmol·L-1·h-1，应用稀释速率控制策略后，生产强度达到101.10 mmol·L-1·h-1，极大地提高了发酵性能。

表2 不同稀释速率策略下的稳态值对比Table 2 Comparison of steady values of metabolites under different strategies for dilution rate

另一方面，稀释速率反馈控制策略极大地缩短了发酵体系达到稳态的时间，这在控制理论中被称为“调整时间”（settling time），是系统动态性能的综合指标。调整时间的缩短，意味着发酵系统能够更快速地进入稳态，提高整体的培养性能。在固定稀释速率的情况下，甘油以恒定速率（即D）被输入到反应器中，但发酵初期，生物量有限，转化的甘油也极为有限，此时大量的残余甘油被排出反应器，造成极大的浪费。如图3所示，在采用反馈控制策略后，稀释速率是动态变化的。在发酵初期，稀释速率从较小值开始提高，甘油随着稀释速率的调整，逐步提高流加量，这与反应器中微生物的增殖趋势是一致的。在这个阶段，甘油流加量的变化是与微生物的转化能力匹配的，也就是“按需分配”甘油。同时由于稀释速率不高，流出的发酵液的体积有限。从图2还可以看出，反馈控制使得调整时间由原来的81.27 h缩短到了34.11 h（幅度超过50%），避免了30多小时的甘油损耗，有利于提高发酵性能。此外，采用恒定稀释速率的发酵过程，其超调量较大，施加控制手段后，超调量明显减小，同样有利于提高发酵性能。

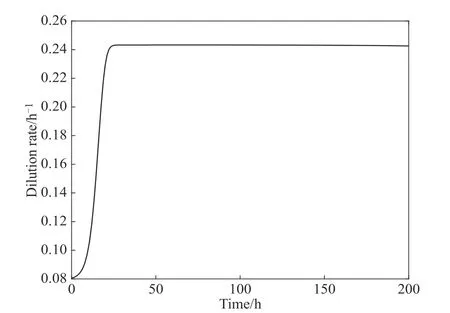
图3 受控稀释速率的变化过程Fig.3 Variation of the controlled dilution rate during the fermentation

3 结 论

提出了一种K. pneumoniae连续发酵甘油生产PDO 的自动化控制策略。首先通过数学函数连续性分析工具预测了该过程的多稳态特性，结果表明在不同的初始甘油浓度或稀释速率下，系统均会出现多稳态现象，通过双因素分析，获得了多稳态出现的临界区域，该区域内部的稳态是不稳定的，在实践操作中可以依此选择合适的工作点。在此基础上，基于反馈控制理论，设计优化了受残余甘油和产物PDO 及乙醇浓度影响的稀释速率反馈控制策略，该策略可作为实践中连续培养的进料方案，经自动控制的稀释速率在提高产物浓度的同时，极大地缩短了系统达到稳定的调整时间，可大幅度降低发酵初期阶段甘油的浪费，提高了发酵过程的甘油的转化率和生产强度。