基于波箔片变形的浮动式箔片气膜密封性能分析

徐洁，俞树荣，丁雪兴，蒋海涛，丁俊华

（兰州理工大学石油化工学院，甘肃兰州 730050）

引 言

航空发动机的设计一直是综合强国优先发展的重大项目[1-2]，而先进的动密封技术是航空发动机研发的重要组成部分，也是影响航空发动机性能以及使用寿命的关键[3-4]。浮动式气膜密封，通过锲形间隙的动压润滑作用使转子和浮环保持分离状态，并利用带压气膜实现非接触密封[5]，因而在火箭涡轮泵、航空发动机系密封组件中得到了很好的应用[6-7]。但由于航空飞行器在运行过程中容易受到环境因素和自身结构带来的随机不确定性激励[8-9]，机体俯仰角、偏航角、滚转角的微小变化都可诱发失稳，从而导致浮环气膜密封失效，影响整机工作[10]。

为提高运行的可靠性，国内外学者设计新型密封结构增强位移的包容性，其主流设计思路是用弹性结构代替或者支撑刚性密封端面。早在20 世纪90年代，NASA 基于箔片气体径向轴承的设计原理，针对航空发动机的应用，Salehi 等[11-12]提出了弹性箔片密封（compliant foil seal,CFS）结构，后期，美国宇航局格伦研究中心分别在发动机模拟工况条件[13]和室温条件[14]下进行了密封试验，表明其在高温和大压差下表现良好。Roberts 等[15]设计了具有柔性环形壁的密封件，这种柔性环形壁主要由单列独立固定的弹性元件周向排列组成，它在保证足够载荷的同时，允许燃气涡轮发动机和排气喷嘴之间的相对偏转。Fang 等[16]在原有CFS 的设计基础上，改变波箔片的方向，即拱波不再沿轴向布置，而是沿周向布置。此外，为了适应转子偏移，也有学者沿用传统刚性浮环，设计具有较大弹性的支撑系统来吸收径向位移的振动能量。王虹等[17]将金属橡胶弹性外环等效为阻尼器，提出一种新型气膜密封阻尼结构(GFSD)，采用Newton-Raphson 法求解密封性能，并与直通式篦齿密封相比，结果表明压力越大，GFSD表现越优异。Salehi 等[18]针对高速工况下的CFS 进行考虑湍流效应的密封性能计算，利用逐次超松弛求解流场和流体膜厚度的控制方程，发现压差大于75 psi(1 psi=6.895 kPa)时，泊肃叶流占主导地位。马纲等[19]设计了在密封支座连接柔性支撑的柱面密封，并利用有限元的数值方法求解瞬态雷诺方程，分析了密封系统稳定性与密封环质量之间的关系。张大鹏[20]分别进行了具有优化动压槽的刚、柔性支承浮环密封试验，并测试泄漏量，发现二者泄漏量变化趋势基本保持一致，且柔性支承结构可有效减缓工况突变带来的影响。近年来，昆明理工大学团队关于柔性浮动式气膜密封的探究较多，例如，康宇驰等[21]设计了分离式的浮动式箔片气膜密封，且将波箔片沿圆周方向分段固定；Wang 等[22]分析了层流等温下的T 型槽弹性箔片气膜密封的静、动态性能，表明了加长密封宽度可有效改善密封性能，但并未阐述箔片端面的相关参数和变形计算方式；同时，该团队还将金属鼓泡等作为柔性支撑结构[23-24]，并利用ANSYS软件建立流固耦合数值模拟模型，分析了不同柔性支撑结构对浮动式气膜密封流场以及密封环的影响。综上所述，关于弹性箔片气膜密封的研究主要集中在结构设计方面，除美国NASA 进行了部分理论和试验测试外，国内学者也开展了柔性支撑密封的相关研究，但现有公开的弹性箔片气膜密封的成果较少。

本文基于CFS 结构，根据弹性箔片气膜密封的弹性端面结构和动压槽型，同时考虑波箔片的刚度和阻尼，在柱坐标系下建立一端固定的波箔片和转子进行同步圆运动时的气膜厚度模型，并利用有限差分法与压力雷诺方程联立求解静、动态密封性能参数。在平箔片表面的进口位置和中间位置分别开设直线动压槽，考察两种不同动压槽位置对锲形间隙内润滑气体厚度和动压分布的作用情况，探寻压力、转速、摩擦因数和波箔片厚度对弹性箔片气膜密封润滑性能的影响规律。

1 浮动式箔片气膜密封

1.1 结构分析

图1 所示为浮动式箔片气膜密封结构，主要是由密封腔、弹性波箔片、支承平箔片以及转子系统组成。其中，转子偏心安装在腔体中，波箔片沿轴向分离且一端固定至密封腔体上，平箔片呈完整的环状，并将高压侧的平箔片进行延伸，形成限制位移的延伸段，密封支座压紧平箔片延伸段实现平箔片和波箔片的固定。借鉴刚性柱面气膜密封动压槽的设计，在平箔片表面开设性能较好的单列直线动压槽[25]。

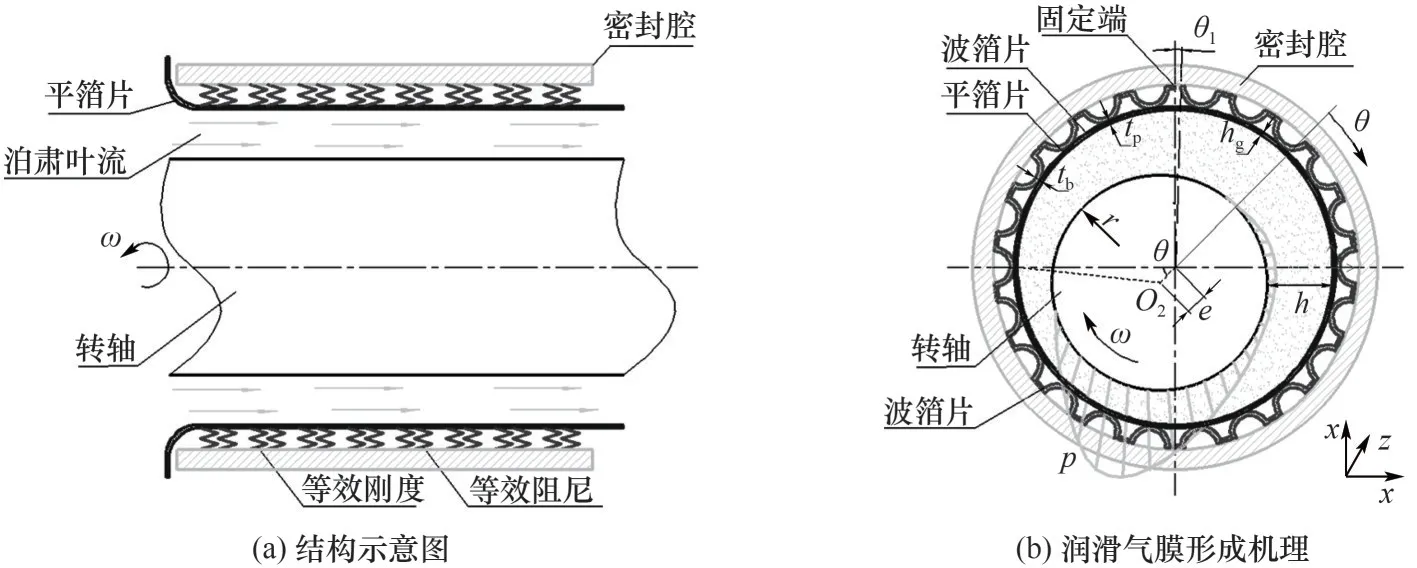
图1 浮动式箔片气膜密封Fig.1 Floating foil gas film seal

1.2 工作原理

波箔片顶部均与平箔片接触，当在平箔片表面施加压力载荷作用后，平箔片和波箔片会在受力方向发生变形，并从各自的固定端至自由端出现微小滑移[26]，如图2 所示。当弹性箔片气膜密封处于正常工作状态时，气体介质从高压侧流至低压侧，弹性箔片气膜密封由于偏心距、动压槽以及箔片变形的共同作用，在转子与平箔片的微间隙内形成微米级环状带压气膜，保证了密封摩擦副始终处于分离状态，以此实现润滑和密封的效果[27]。

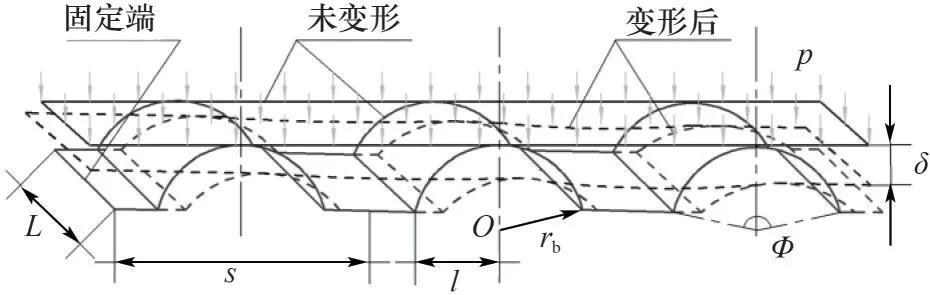
图2 弹性箔片变形示意图Fig.2 Schematic diagram of elastic foil deformation

2 理论模型的建立

2.1 箔片刚度模型

忽略平箔片在径向方向的凹陷或凸起，仅考虑波箔片的变形。根据图1，考虑波箔片与密封腔体的库仑摩擦作用，利用Iordanoff[28]波箔片一端固定、一端自由的刚度模型表征波箔片的变形，如式(1)所示。

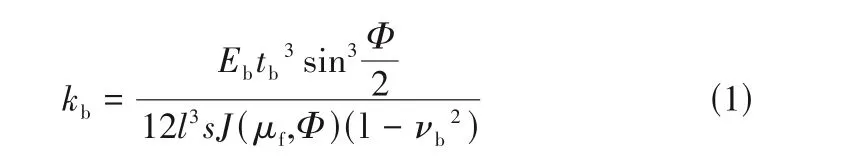
式中，J为与波箔片角度Φ与摩擦因数μf有关的函数，如式(2)和式(3)所示。

2.2 密封特性求解模型

假设流场为层流，流固界面间无滑移，密封介质为理想气体，物性参数保持不变，可得流体动压润滑模型：

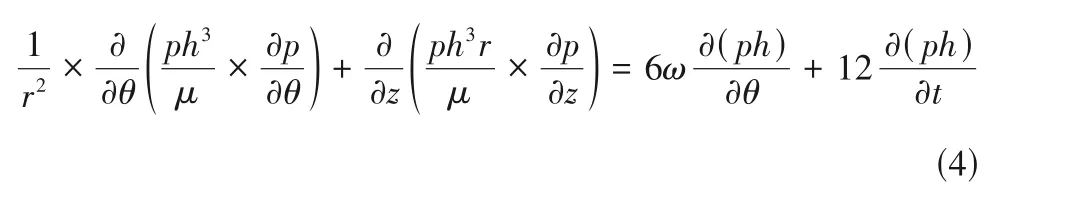
式中，p为计算得到的静态气膜压力，Pa；t为运动时间，s。涡动频率比为1。

相较于传统浮动式气膜密封，弹性箔片密封的气膜厚度还需考虑箔片变形的影响，因而，静态时槽区和非槽区的气膜厚度可通过式(5)计算。

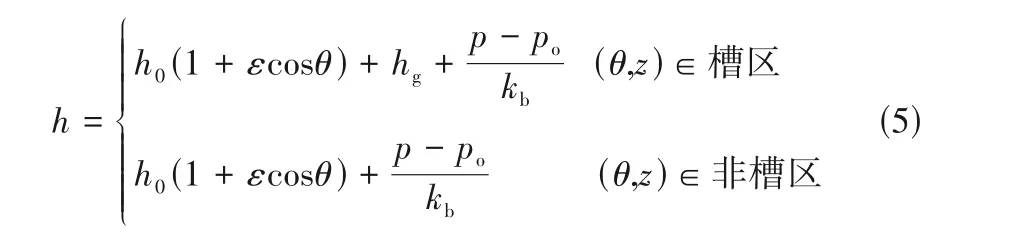
当受到(Δx,Δy)的位移扰动和(Δx˙,Δy˙)的速度扰动后，得到包含扰动参数的气膜压力、气膜厚度以及箔片变形量的Taylor级数展开式

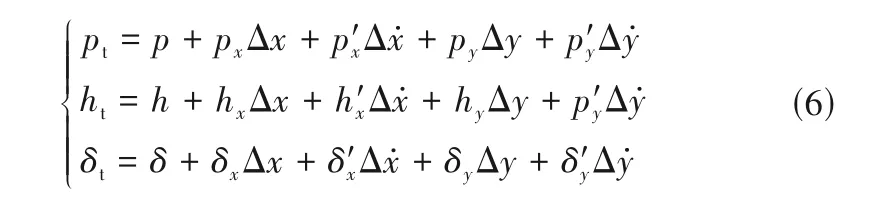
考虑时间项后，气膜厚度偏离静态气膜厚度h，得到微扰下的气膜厚度

式中，Δh= Δxsinφ- Δycosφ；δt为由扰动引起的波箔片变形量，μm。联立式(6)、式(7)可得

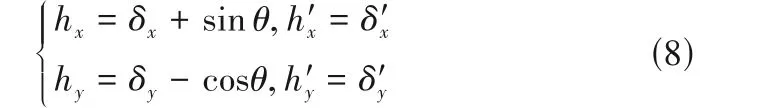
扰动条件下波箔片的力平衡方程为

式中，[kb]，[cb]分别为波箔片的刚度矩阵和阻尼矩阵，cb= 5.00 × 106Pa · s/m；{F}为气膜压力矢量。

将式(6)、式(8)代入式(9)，可得：

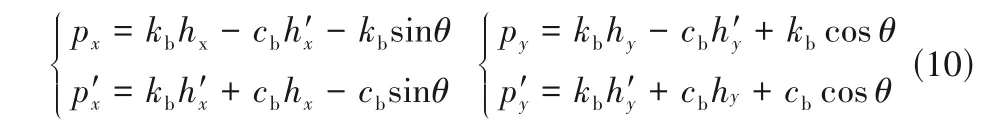
2.3 密封性能参数

评价浮动式箔片气膜密封的关键静态特性参数有气膜浮升力和质量泄漏率，动态特性参数有主刚度和主阻尼系数，以下为各表达式。

气膜浮升力

式中，Fh，Fv分别为气膜浮升力的水平方向和竖直方向的分量。

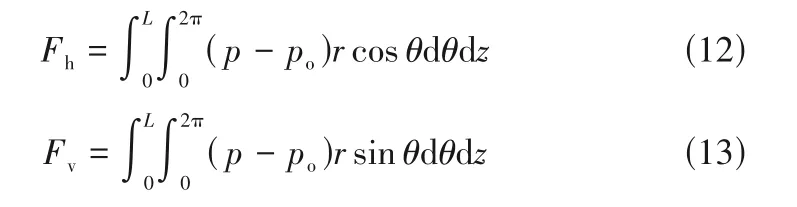
质量泄漏率

气膜主刚度系数

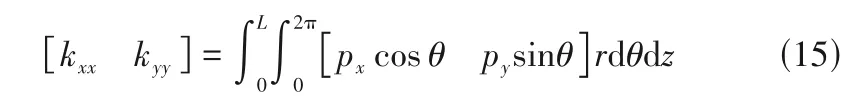
气膜主阻尼系数

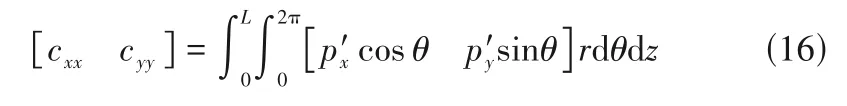
2.4 边界条件

在进出口有强制性边界

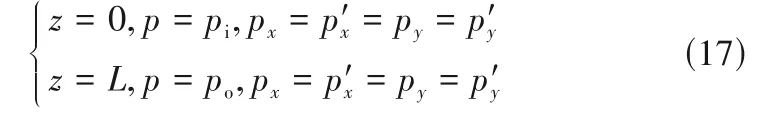
在中截面有循环边界

2.5 网格划分与迭代计算

沿周向和轴向划分网格数，如图3所示。

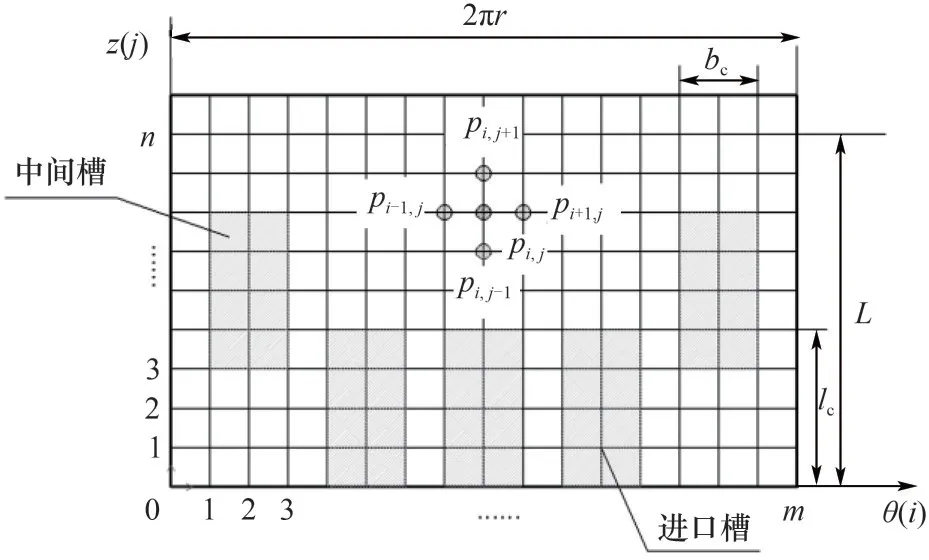
图3 计算域网格划分Fig.3 Computational domain meshing

利用有限差分法对静、动态求解方程进行离散，并在迭代计算时采用超松弛迭代：

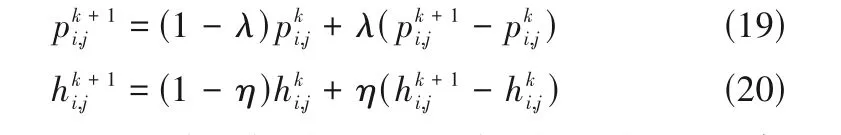
式中，λ，η分别为气膜压力和气膜厚度的迭代因子；k为迭代次数。浮动式箔片气膜密封的特性参数计算流程如图4所示，图中err= 1 × 10-6。

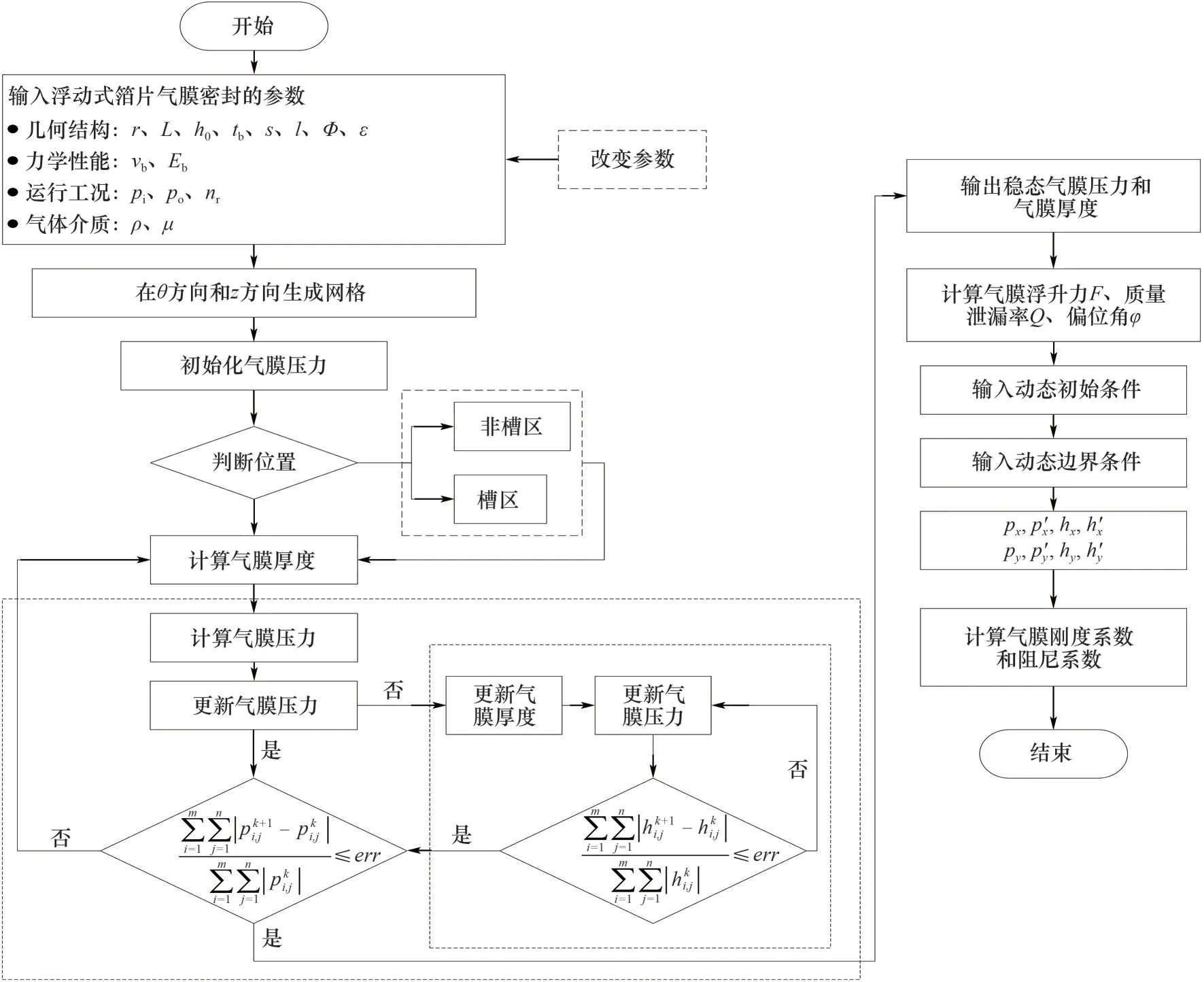
图4 计算流程图Fig.4 Calculation flow chart

3 参数选取与讨论

3.1 结构参数与力学性能

浮动式箔片气膜密封的结构参数和力学性能如表1所示。

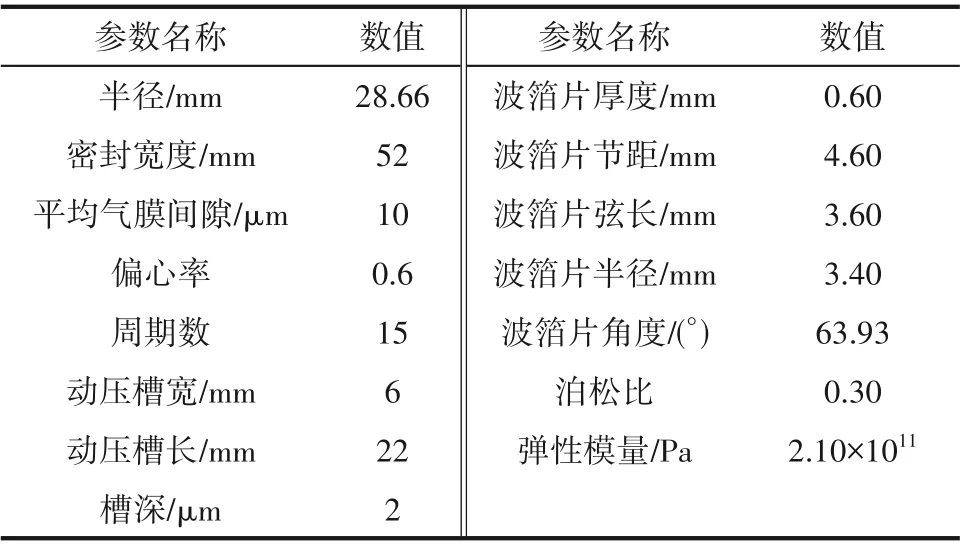
表1 结构参数与力学性能Table 1 Structural parameters and mechanical properties

3.2 工况参数

表2 为浮动式箔片气膜密封的工况参数(介质为空气)。

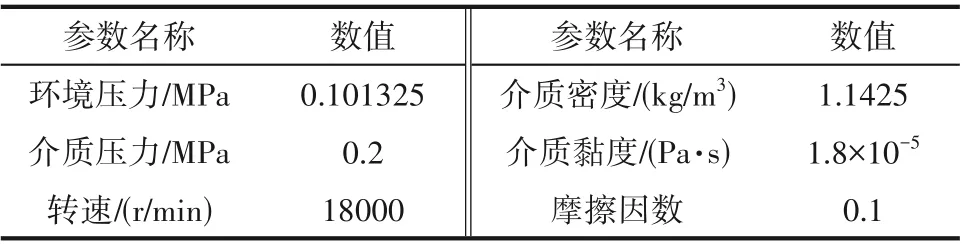
表2 工况参数Table 2 Working condition parameters

3.3 程序正确性验证

3.3.1 流场计算程序验证 为验证流场计算的正确性，选择文献[29]中无槽刚性浮环的结构参数进行流场计算程序的正确性验证，对比结果如图5 所示。当偏心率为0.5 时，有最大相对误差(P)为5.76%，表明本文流场计算程序具有一定可靠性。

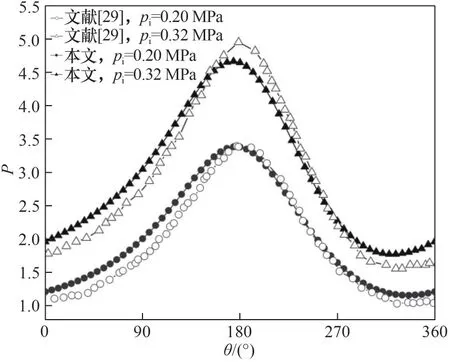
图5 流场计算程序验证Fig.5 Verification of flow field calculation program

3.3.2 刚度计算程序验证 选择文献[30]中的波箔片结构参数，验证波箔片刚度模型和计算程序的正确性，对比结果如表3 所示，同时，闫佳佳[30]针对径向箔片轴承进行研究时利用该刚度模型进行计算，并与NASA 试验数据[31]对比验证了准确性，说明该刚度模型具有一定的可用性。

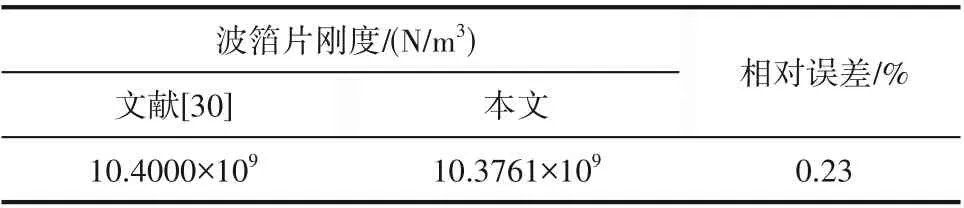
表3 刚度计算程序正确性验证Table 3 Verification of the correctness of the stiffness calculation program

4 计算结果与分析

以表1、表2 的工况参数和结构参数进行计算，获得进口直线槽和中间直线槽的波箔片变形分布如图6 所示，气膜厚度分布如图7 所示，气膜压力分布如图8所示。

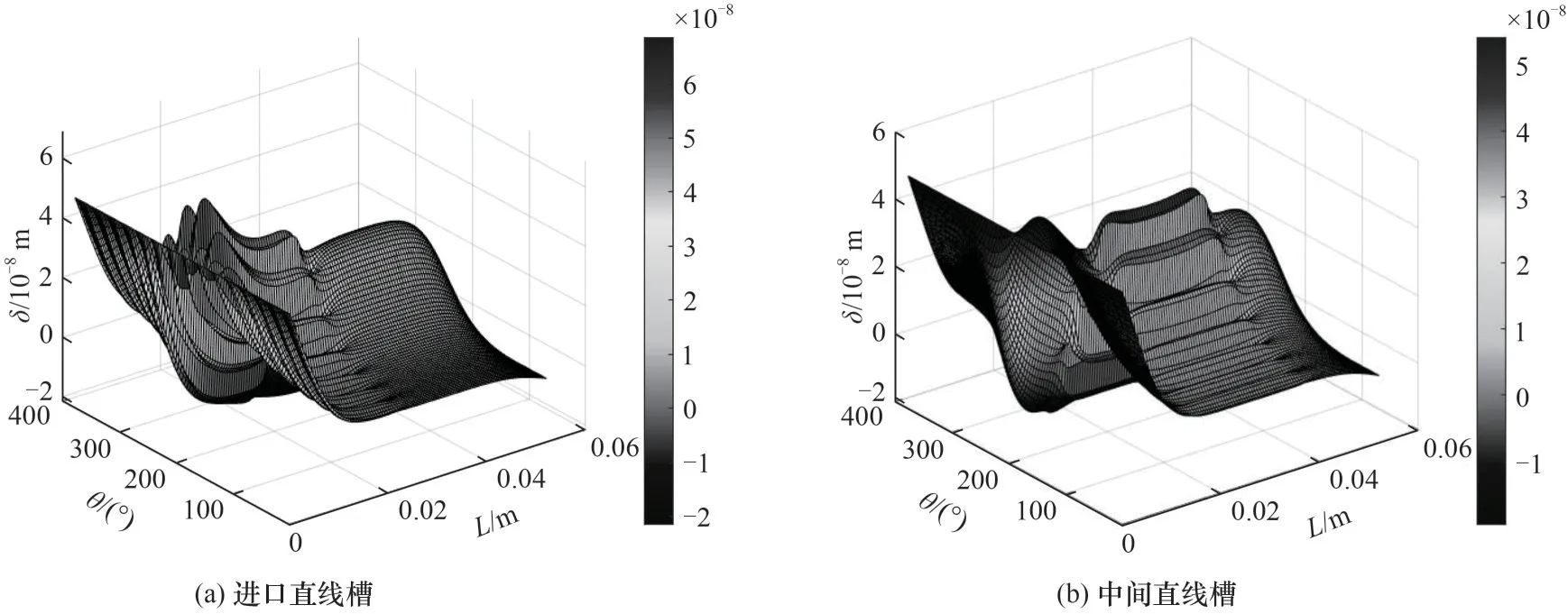
图6 波箔片变形分布Fig.6 Distribution of bump foil deformation

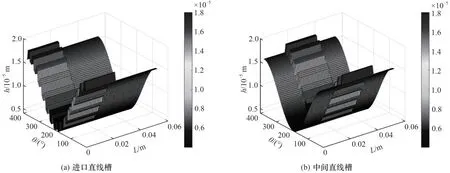
图7 气膜厚度分布Fig.7 Distribution of gas film pressure

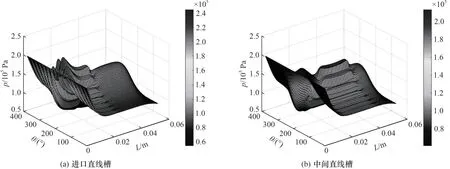
图8 气膜压力分布Fig.8 Distribution of gas film pressure

由于直线槽分布位置的不同，所表现出来的流场特性也有所不同。对比图6、图7 可以发现，在气膜厚度分布的最小区域，存在最大的波箔片变形量，但气膜厚度沿着圆周方向呈余弦状，整体分布表现出更强的对称性，由于动压槽的存在，气膜厚度在微尺度台阶处出现不连续性。两种直线槽最小气膜厚度均位于压力出口处，进口直线槽的最大和最小气膜厚度分别为18.02 和4.00 μm，中间直线槽的最大和最小气膜厚度分别为17.97和4.00 μm。

根据图8 气膜压力分布所示，在θ=180°位置的高压侧附近，出现最大气膜压力，压力在动压槽区域呈现一定幅度的波动，随着圆周角度向对称边界变化，气膜厚度逐渐增大，气膜压力逐渐减小，压力波动幅值逐渐减小。对比图8(a)、(b)，在动压效应和锲形效应的共同作用下，气体流动至进口直线槽后，气膜压力略微上升，在压力进口附近有气膜压力最大值(0.24 MPa)，之后缓慢减小，当气体流经动压槽根部之后，由于节流效应气膜压力明显下降，直至在密封端面的末端部分达到环境压力。对于分布有中间直线槽的流场，最大气膜压力为0.21 MPa，气膜压力从进口处就开始缓慢减小，当气体流入中间直线槽后气膜压力小幅度增大，随后缓慢减小。同时可以发现，流体域内的气膜压力并不是完全大于环境压力，而是在气膜压力较高区域附近出现了负压，这是由于偏心作用和压差作用导致的，吸附效应使得波箔片发生变形，气膜厚度也在负压分布区域减小。

4.1 进口压力的影响

图9(a)给出了不同直线槽分布位置下气膜浮升力、质量泄漏率与进口压力的关系曲线。当进口压力在0.12～0.26 MPa范围内变化时，进口直线槽的气膜浮升力和质量泄漏率始终大于中间直线槽。随着进口压力上升，气膜浮升力也呈单调性上升趋势，进口直线槽的气膜浮升力增加了8.86%，中间直线槽的气膜浮升力增加了8.32%，可见，进口压力变化引起的气膜浮升力变化幅度较小，这是由于进口压力越大，波箔片背离轴心方向的变形越大，从而气膜厚度越大，这在一定程度上削弱了进口压力带来的整体流域内压力的增大效应。进口压力增大加速了径向的泊肃叶流动，较多的气体介质从高压侧流至低压侧，同时，密封面的变形也导致泄漏通道增大，因而进口压力对质量泄漏率的影响显著，进口直线槽的泄漏率从1.48×10-4kg/s 增加至2.16×10-3kg/s，中间直线槽的泄漏率从1.30×10-4kg/s增加至1.72×10-3kg/s，当进口压力较小时，两种动压槽位置的泄漏率计算结果差值较小，相较于分布在中间位置的直线槽，高压侧附近的进口直线槽更容易受到进口压力的影响，泄漏率增幅更大。

图9(b)给出了动态特性参数与进口压力的关系曲线，进口直线槽和中间直线槽的主刚度kxx为正、主刚度kyy为负，且二者具有相似的变化规律，低压工况下两种动压槽位置的主刚度kxx差别很小，之后均随进口压力的升高而缓慢降低，其中进口直线槽的下降速率更快，这说明进口压力增大气膜厚度迅速增大，当进口压力为0.26 MPa 时，进口直线槽有最小刚度系数4.66×106N/m，中间直线槽有最小刚度系数4.47×106N/m。进口直线槽和中间直线槽的主阻尼cxx与主阻尼cyy变化趋势呈对称状态，且均逐渐趋于零。

图9 进口压力的影响Fig.9 Influence of inlet pressure

4.2 转速的影响

由图10(a)可以看出，当转速从8000 r/min 增大至22000 r/min 时，气膜浮升力显著提高，且基本呈线性增大趋势，进口直线槽的气膜浮升力增加了2.99 倍，中间直线槽的气膜浮升力增加了3.09 倍。由于加速的库埃特流动对轴向方向的流动影响很小，因而质量泄漏率基本不随转速的增大发生改变。其中，进口直线槽的质量泄漏率维持在1.11×10-3kg/s，中间直线槽的质量泄漏率维持在0.89×10-4kg/s。转速增大，气体动压效应增强，最大气膜压力迅速增大，阶梯效应增强，高压附近区域的最小气膜压力也随之减小，但承压区域比负压区域的面积增率大[32-33]，因而浮动式箔片气膜密封的浮升力随转速的增大而增大。转速增大引起的这种流场现象也导致浮动式箔片密封的气膜主刚度kxx和kyy的绝对值均随着转速的增大而增大。由图10(b)可以看出，主阻尼cxx和cyy均随着转速的升高从负值上升为正值，呈现出抛物线式的上升趋势，并逐渐趋于平稳，说明浮动式箔片密封适应高转速的工况条件。

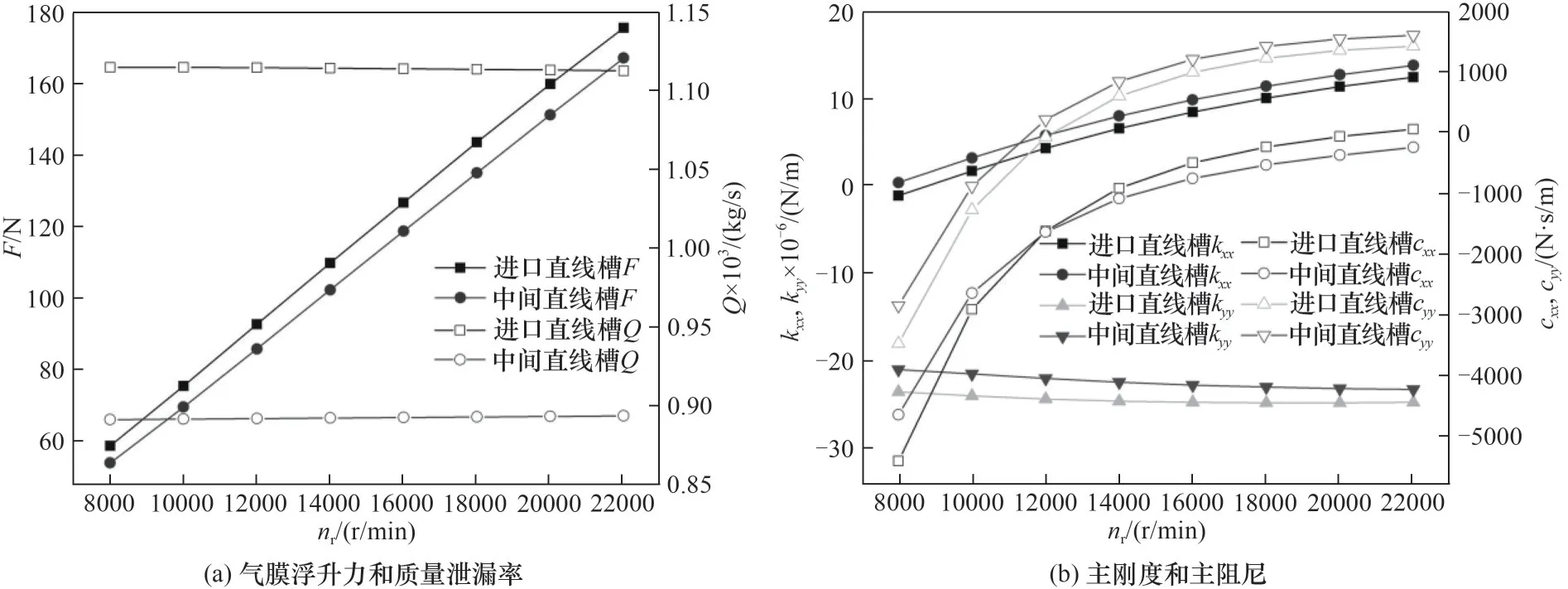
图10 转速的影响Fig.10 Influence of speed

4.3 摩擦因数的影响

图11(a)给出了库仑摩擦因数与浮动式箔片气膜密封静态密封特性的关系，随着摩擦因数的不断增加，进口直线槽和中间直线槽的质量泄漏率均呈现出略微下降的趋势，减小量可以忽略不计。在实际运行过程中，由于波箔片发生滑移，必定与发生接触的密封腔间存在库仑摩擦，这在一定程度上增大了波箔片的刚度，箔片变形量减小，最大气膜厚度和最小气膜厚度均减小，锲形效应加强，因而气膜浮升力增大。当摩擦因数从0 增大至0.28 时，进口直线槽和中间直线槽的浮升力分别增大了1.74 和1.40 N，说明摩擦因数变化对气膜浮升力的影响很小。

图11(b)给出了库仑摩擦因数与浮动式箔片气膜密封动态密封特性的关系，摩擦因数增大，两种直线动压槽对应的气膜主刚度kxx和kyy都轻微提高，并保持相对稳定的差值，中间直线槽的主刚度均大于进口直线槽，主阻尼反而均小于进口直线槽，究其原因，摩擦因数增大，气膜厚度增大量较小，使得气膜阻尼效果变弱。

图11 摩擦因数的影响Fig.11 Influence of friction factor

4.4 波箔片厚度的影响

图12(a)为波箔片厚度在0.20～0.90 mm 范围内变化时对各关键参数的影响规律，从图中可以看出，波箔片厚度增大，增强了结构自身在径向方向的支撑能力，使得弹性端面不易在受力方向产生位移，加强了锲形效应，因此气膜浮升力提升，质量泄漏率减小，当波箔片为0.90 mm 时，进口直线槽有最大气膜浮升力127.99 N 和最小质量泄漏量1.11×10-3kg/s，中间直线槽有最大气膜浮升力119.93 N和最小质量泄漏量0.89×10-3kg/s，但这种加压和控漏作用不是无限加强的，而是逐渐变缓的，说明当波箔片厚度趋于某一较大值时对端面刚度的影响减弱，甚至不发生影响，密封端面接近刚性化。

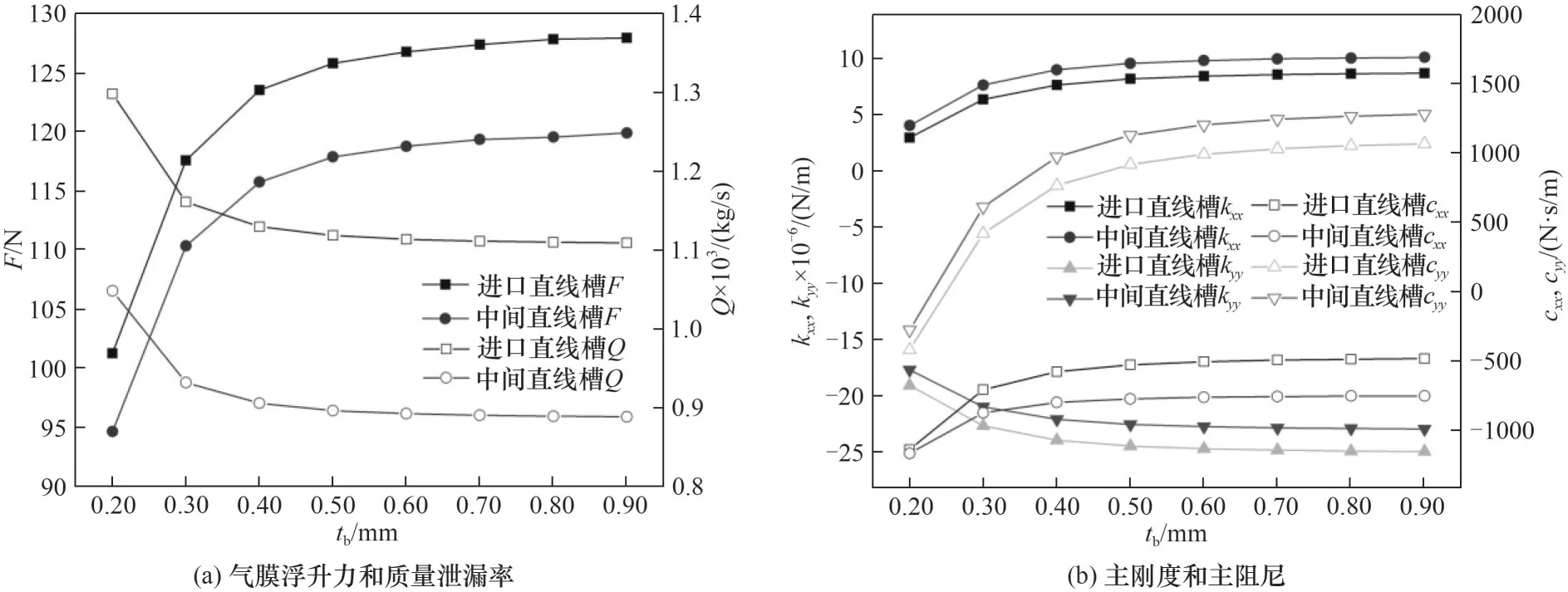
图12 波箔片厚度的影响Fig.12 Influence of bump foil thickness

从图12(b)可以看出，气膜主刚度kxx、主阻尼cxx和cyy均随着波箔片厚度的增大而增大，密封端面不易变形，密封间隙增量减小，导致气膜的承载力上升，所以气膜主刚度的绝对值大小将会有所上升。对于进口直线槽，0.90 mm 波箔片厚度的主刚度kxx均为0.20 mm 的2.89 倍，主刚度kyy均为0.20 mm 的1.01 倍；对于中间直线槽，0.90 mm 波箔片厚度的主刚度kxx均为0.20 mm 的2.49 倍，主刚度kyy均为0.20 mm 的1.30 倍，这是由于浮动式箔片气膜密封承担的主要载荷作用在x方向上，因此主刚度kxx的增幅略大于主刚度kyy。

5 结 论

本文研究主要得到以下结论。

(1)浮动式箔片气膜密封的密封特性与流场分布和密封端面的变形相关，在最小气膜厚度处，气膜压力最大，对应的波箔片变形最大。

(2)进口直线槽的气膜浮升力和质量泄漏率均大于中间直线槽，进口直线槽对进口压力的变化更敏感。

(3)在浮动式箔片气膜密封中，库仑摩擦效应使密封副表面变“刚”，但相比于库仑摩擦效应的影响，波箔片厚度增大，刚度的增大效果更加明显，对密封性能的影响也更大。

(4)气膜浮升力和质量泄漏率均随着进口压力增大而增大，但气膜主刚度反而减小；气膜浮升力、气膜主刚度kxx以及主阻尼均随着转速的增大而增大，而主阻尼逐渐趋于稳定，转速变化对质量泄漏率基本不发生影响。

(5)较大的摩擦因数和波箔片厚度，密封端面的变形量减小，气膜厚度增量减小，动压效应增强，气膜浮升力、主刚度以及主阻尼在小范围内增大。

(6)为满足高速高温环境下航空发动机的轴端动密封设计，还需考虑平箔片的弯曲变形，并结合试验完善修正，从而建立更精确的浮动式箔片气膜密封数值计算模型。

符 号 说 明

bc——槽宽，mm

cb——阻尼系数，Pa·s/m

cxx，cyy——气膜阻尼，N·s/m

Eb——波箔片弹性模量，GPa

e——偏心距

F——气膜浮升力，N

{F}——气膜压力矢量

Ff——摩擦力，N

h——气膜厚度，μm

hg——动压槽槽深，μm

h0——平均气膜厚度，μm

k——迭代次数

kb——波箔片刚度，N/m3

kxx，kyy——气膜刚度，N/m

L——密封宽度，mm

l——波箔片弦长的一半，mm

lc——槽长，mm

nr——转速，r/min

p——气膜任意一点压力，MPa

pi——进口压力，MPa

po——出口压力，MPa

Q——质量泄漏率，kg/s

r——旋转轴半径，mm

rb——波箔片半径，mm

s——波箔片节距，mm

t——运动时间，s

tb——波箔片厚度，mm

tp——平箔片厚度，mm

vb——波箔片泊松比

z——轴向坐标

δ——箔片变形量，μm

ε——偏心率

η——气膜厚度迭代因子

θ——周向角度，(°)

θ1——波箔片自由端与固定端形成的角度，(°)

λ——气膜压力迭代因子

μ——介质黏度，Pa·s

μf——波箔片与密封腔的摩擦因数

ρ——介质密度，kg/m3

Φ——波箔片角度，(°)

φ——偏位角，(°)

ω——转速，rad/s

下角标

h——水平方向

t——动态相关参数

v——竖直方向

x——x方向微扰分量

y——y方向微扰分量