基于混合建模的水泥生料分解过程动态特性研究

戚子豪，钟文琪，陈曦，周冠文，赵小亮，辛美静，陈翼，朱永长

（1 东南大学能源热转换及其过程测控教育部重点实验室，江苏南京 210096；2 中国中材国际工程股份有限公司（南京），江苏南京 211106）

引 言

水泥是基础设施建设不可缺少的重要原材料，分解炉作为新型干法水泥生产线中承担燃料燃烧和生料分解任务的核心设备，其运行水平的高低决定了水泥生产的效率和污染物排放强度，因此，有必要对水泥生料分解过程涉及的动态特性进行研究。

现有研究已经对循环流化床[1-6]、煤粉锅炉[7]、垃圾焚烧炉排炉[8-9]等多种工业炉窑建立了不同维度的机理模型，并基于机理模型对动态特性进行了分析。相比之下目前对于分解炉的整体建模及动态特性的研究相对较少，内容集中在分解炉内部反应与流动的机理分析方面。Jensen[10]提出了分解炉内的均相反应数学模型，对炉内的气固非均相反应进行了大量简化。Iliuta等[11-13]开发了基于焦炭燃烧和石灰石煅烧的扩散反应数学模型，使用Nieuwland等[14]提出的轴向扩散模型来描述分解炉内的气固流动，研究了操作参数对分解炉内煅烧效率及污染物排放的影响规律。前人建立的炉内流动过程模拟方程较为复杂，需要求解大量偏微分方程，难以满足实时调控的要求。此外，分解炉炉型众多，结构复杂，前人总结的炉内气体与颗粒流动经验公式适用范围较小，无法满足特定研究对象的计算需要。部分研究者基于数据驱动的方法对水泥分解炉建模展开研究。Fellaou 等[15]基于统计学习的方法，通过分析历史运行数据和实验设计数据，对分解炉运行参数优化进行研究。Hao 等[16-17]建立水泥分解炉深度信念网络计算模型。He 等[18]使用卷积神经网络与长短期记忆神经网络相结合的方法对NOx排放量进行预测。这类黑盒模型具有较高的计算精度，但物理意义并不明确，难以充分揭示分解炉反应的内在机理。

近年来，混合模型在复杂过程建模中得到广泛应用。一些学者将神经网络与反应机理相结合，求解化工过程中的未知参数[19-23]，简化了模型的求解难度，提高了计算的准确性。混合模型将白盒模型与黑盒模型结合，利用先验知识和过程数据建立过程的动态模型，同时具有物理意义明确、泛化能力强和模型复杂度低的优点[24-26]。在此类方法中，可利用黑盒模型对机理模型中的中间变量进行估计，只需要确定机理模型的基本结构，涉及的先验知识相对较少，适用于过程机理较为复杂的化工流程建模，且已受到较为广泛的重视和研究。前人在上述化工过程中应用的混合建模方法也为水泥分解炉模型的建立提供了思路。

本文在总结前人关于分解炉内化学反应与气固流动机理相关研究内容的基础上，引入神经网络方法，提出一种机理与数据相结合的水泥分解炉混合建模方法。利用已有的先验知识确定分解炉计算模型的结构，使用神经网络这一黑盒模型对煅烧过程中的气固流动参数等中间变量进行预测，并将预测所得的流动参数与煤炭燃烧、生料分解、传热过程以及守恒方程等模块的计算相互耦合，建立一维的混合模型。基于该模型对分解炉内的参数分布规律及关键操作变量动态响应特性进行研究，为分解炉控制系统的设计与运行调控提供理论支撑与依据。

1 水泥分解炉模型

1.1 分解炉模型机理分析

1.1.1 模型简化与假设 由于实际化工流程过于复杂，为了便于模型计算，基于已有的石灰石分解、煤炭燃烧等化学、热力学机理，提出以下简化与假设。

（1）假设分解炉内同一截面上参数分布均匀，分解炉内温度、烟气成分以及物料物性参数等只沿分解炉轴向方向变化，即将三维空间分布简化为沿分解炉轴向的一维分布。

（2）沿气体轴向流动方向，将分解炉划分为若干个控制体，如图1所示，对每一控制体求解质量与能量平衡方程。

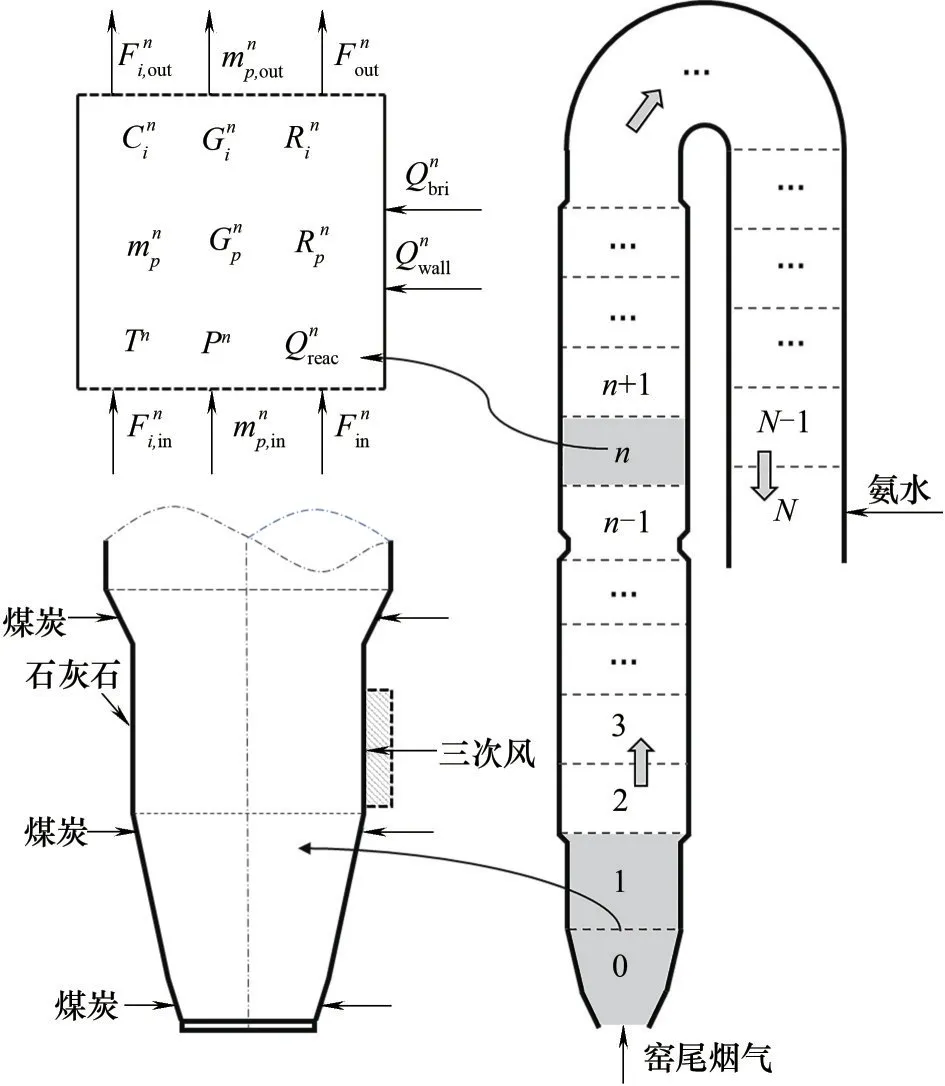
图1 分解炉模型及控制体划分Fig.1 Precalciner model and division of control volume

（3）假设模型中涉及的气体均满足理想气体状态方程。

（4）假设焦炭、石灰石、氧化钙等颗粒均为球形颗粒，并假设同种颗粒具有均一的粒度。

（5）由于分解炉内温度一般低于1600 K，热力型NOx和快速型NOx的反应速率很低，炉内计算时仅考虑来自回转窑的烟气带入的NOx与分解炉内煤粉燃烧产生的燃料型NOx[27-28]。考虑分解炉炉型及炉内主要物质催化效应对氮氧化物反应速率的影响。

（6）石灰石煅烧过程仅考虑碳酸钙的分解反应，忽略少量碳酸镁的影响并将其他成分均视为惰性物质，不参与炉内反应。

（7）在炉内传热计算过程中采用颗粒团更新模型[29-30]，考虑颗粒团与炉膛壁面之间的对流换热、固体颗粒分散相对流换热、颗粒团覆盖部分壁面所受的辐射换热以及裸露壁面上所受的辐射换热等。

1.1.2 守恒方程 分解炉模型及控制体的划分如图1 所示，在每个控制体内分别建立质量与能量守恒方程。

控制体n中第i种成分的质量平衡可写成：

气体的质量流率Fn可用式(2)进行计算：

其中，wn为气体流速；Dn为炉膛直径；ρ为气体密度。

控制体中主要考虑焦炭颗粒、石灰石颗粒以及氧化钙颗粒的质量平衡：

式中，ςc为颗粒团覆盖壁面的时均份额；hc为颗粒团与壁面的对流传热系数；hcr为颗粒团与被颗粒团覆盖的壁面之间的辐射传热系数；hdc与hdr分别为颗粒分散相对流传热系数与辐射传热系数；hgr为气体与壁面的辐射传热系数。

控制体的总热容量取决于其中的气相组分和固体颗粒含量，可用式(6)计算：

1.1.3 化学反应机理 分解炉内化学反应主要考虑煤粉挥发分析出[31]、挥发分燃烧[32]、焦炭燃烧[33-36]、生料分解[11,37-38]以及氮氧化物的生成与脱除[11-13,39-40]等过程。根据前人对以上各过程化学反应机理的研究，建立分解炉煅烧机理模型。煤粉进入分解炉后经历预热、水分挥发、挥发分的析出与燃烧以及焦炭燃烧等过程，其速率受颗粒粒径、表面氧气浓度、燃烧温度、颗粒孔径多种因素控制。

本研究中假设挥发分析出量随温度的升高而增加，并且认为挥发分近似由CH4、CO、CO2、H2、H2O和tar 组成，各种气体的含量与燃烧速率见附表1 与附表2。

焦炭与氧气的非均相反应采用缩粒模型进行描述，焦炭与气体发生反应后其表面的灰层因为颗粒间的相互碰撞而脱落，未反应的焦炭颗粒与气体进行反应。缩粒模型中焦炭的燃烧速率由气体组分扩散动力学与焦炭反应动力学共同控制，不考虑灰层内部扩散阻力的影响。

焦炭燃烧反应方程式可表示为：

式中，φ为化学机械因子，表征CO2和CO 之间的浓度关系，φ受颗粒粒径与燃烧温度的影响，φ的计算方式以及焦炭燃烧速率计算式见附表1。

一般来说，碳酸钙的分解过程由式(10)来表示：

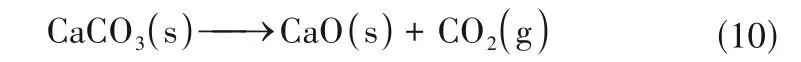
对于较细的石灰石颗粒(＜100 μm)，许多煅烧模型认为颗粒表面温度等于气体温度，并且忽略颗粒内部的温度梯度。在本模型中，碳酸钙的煅烧分解过程由球形颗粒收缩模型描述，碳酸钙煅烧过程分解速率由扩散反应动力学和分子反应动力学两部分决定，碳酸钙反应速率的计算公式见附表1。

附表1 炉内挥发分、焦炭燃烧与碳酸钙分解计算公式Appendix 1 Calculation formulas for volatile matter，coke combustion and calcium carbonate decomposition

分解炉内部的燃烧温度相对较低，生成的热力型NOx与快速型NOx较少，因此在本研究中，仅考虑燃料型NOx的生成。由于氮氧化物反应的机理过于复杂，本研究中对其进行了部分简化，煤炭热解过程中释放出的挥发分氮均按照HCN 进行处理，焦炭中的氮随燃烧过程逐渐释放，忽略部分中间产物的影响，仅考虑NH3、HCN、NO、N2等几个主要产物之间的转化规律。分解炉内大量存在的CaO 及焦炭颗粒能够作为氮氧化物反应的催化剂，对炉内氮氧化物的生成与还原有很大影响，因此在计算炉内氮氧化物质量平衡时需要考虑炉内颗粒的催化效应，具体方程及反应速率见附表2 中式(5)～式(10)。

附表2 炉内均相反应速率Appendix 2 Homogeneous reaction rate in the furnace

续附表2

1.1.4 分解炉内气固多相流 流动模型是分解炉系统数学模型中其他各个子模型的基础，与分解炉内的传热、燃烧以及分解模块相互耦合。结合相关气固流动理论与经验公式[41-42]，认为分解炉内各区域气体流动情况可以用式(11)进行表示：

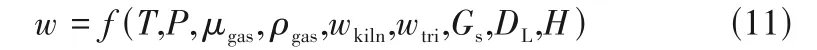
其中，w为烟气的轴向流速；μgas为气体黏度；ρgas为气体密度；wkiln为窑尾烟气流速；wtri为三次风流速；Gs为颗粒质量流率；H为高度；DL为炉膛直径。

分解炉本体结构的直径基本保持不变，但为了加强气体扰动设置了多处缩口，因此引入尺寸修正系数ζ来衡量分解炉结构对流动过程的影响。分解炉内为喷腾与旋流叠加的复杂流动状态，因此通过窑尾烟气流速与三次风流速的比值Θw来量化轴向流速与切向流速的关系。认为气体物性参数是温度的函数均与温度有关，将每一控制体内气体流速进一步简化为：

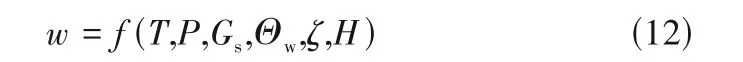
一般情况下，式(12)的拟合需要依靠实验的方法，然而针对不同的炉型和运行条件进行大量工程实验比较困难并且具有局限性。本文将利用神经网络模型理论上可以近似表示任意函数的性质[43]，将原本需要通过实验来拟合的流动经验公式用神经网络模型来表示，假设各层的流动具有相同特性，可用同一神经网络公式进行描述。分解炉内固体停留时间难以测量与计算，工程上通常使用固气停留时间比τ来对颗粒的停留时间进行估算，固气停留时间比τ与分解炉设计参数有关[44]。固体颗粒在每一控制体内的停留时间可用式(13)计算：

其中，tn为颗粒在控制体n内的停留时间；Ln为控制体的轴向长度；wn为气体在控制体内的平均轴向流速。

1.2 混合模型的建立

为解决分解炉内气固流动难以计算的问题，在本研究中使用神经网络模型对炉内的气固流动进行近似拟合，并将神经网络的输出结果代入机理方程中求解控制体内的其他参数。

1.2.1 混合模型结构设计 图2所示为本文所建立的分解炉一维混合模型框架。混合模型的输入参数包括窑尾烟气流速与温度、下料量与下料温度、喷煤量、喷氨量以及三次风量等，混合模型的最终输出为分解炉的出口温度与NOx浓度。

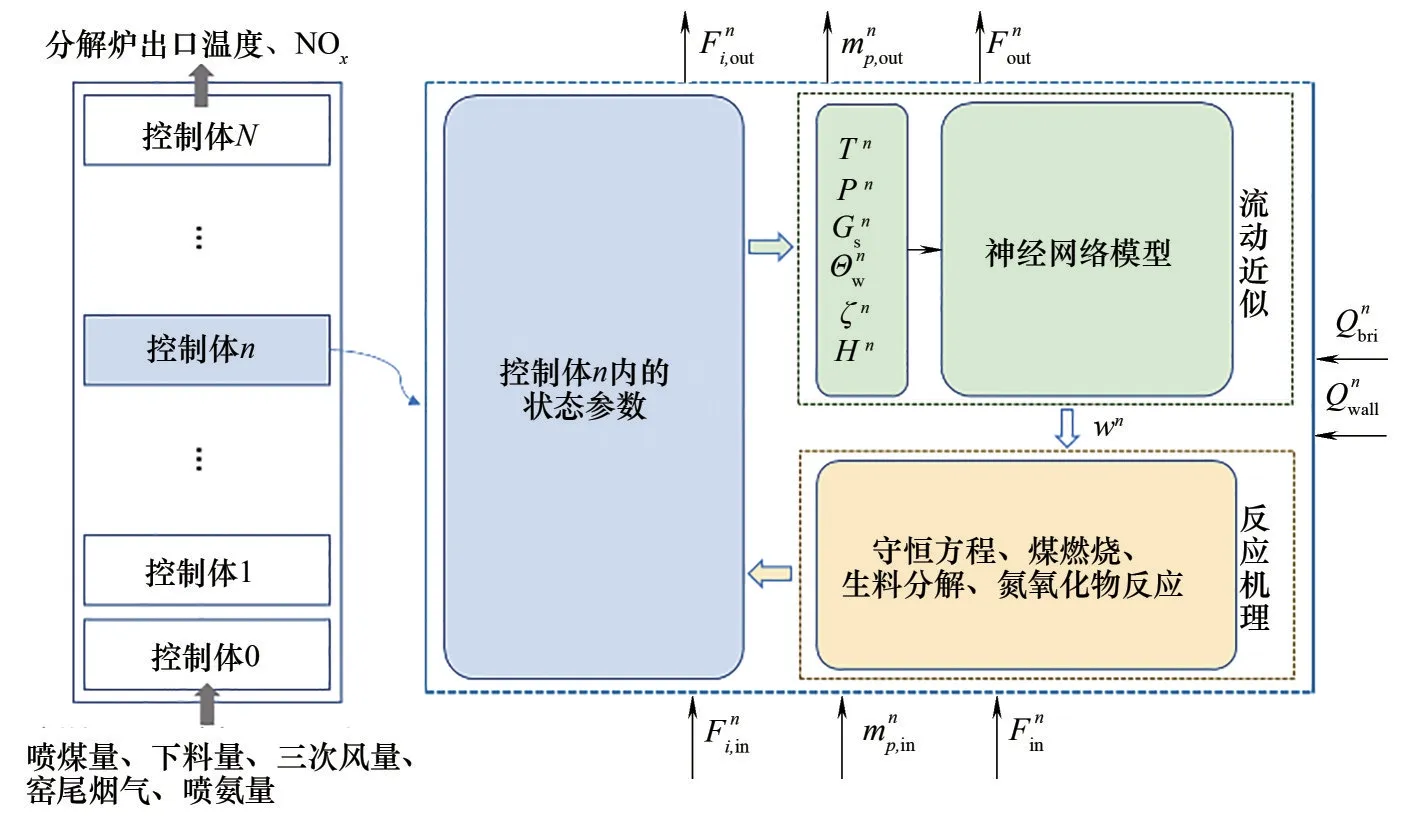
图2 混合模型框架Fig.2 Framework of hybrid model

在每个控制体内，分别基于热力学守恒关系与化学反应方程计算各控制体内的状态参数，其中流动的机理计算用神经网络进行代替。每一控制体内神经网络的输入参数包括Tn、Pn、Θnw、Gns、ξn、Hn，这些值由分解炉机理模型计算得到，神经网络的输出为控制体n内的气体平均流速wn。在求解控制体内的质量守恒方程、传热方程以及停留时间等需要气体流速作为关键参数的机理方程时，将平均流速wn作为中间变量代入，从而计算控制体内的其他各项状态参数。

1.2.2 模型训练方法 在混合模型中每一控制体内建立具有单隐藏层的神经网络，其形式为：

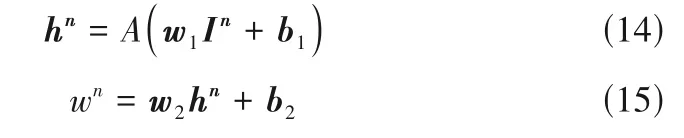
其中，A(·)表示神经网络的激活函数；w1、b1、w2、b2分别为神经网络隐藏层与输出层的权值与偏置；In为控制体n内神经网络的输入，In={Tn,Pn,Θnw,Gns,ξn,Hn}；hn为隐藏层输出；wn为控制体n内神经网络的输出。

模型参数更新过程如图3所示。

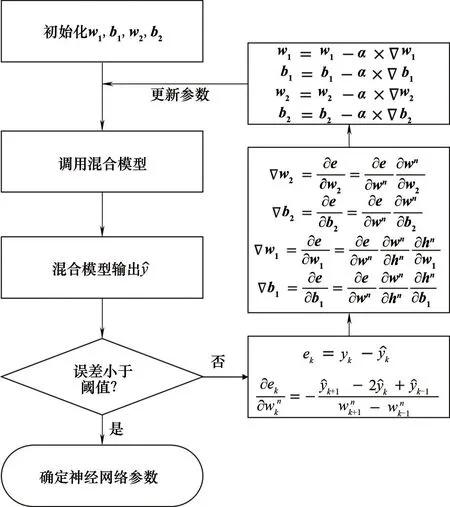
图3 神经网络参数更新过程Fig.3 Update process of neural network parameter

记混合模型在k时刻的真实值与预测值分别为yk与y^k，则混合模型的计算误差ek可表示为：

因此

基于链式求导法则、反向传播算法和梯度下降法，根据式（18），对式（14）和式（15）中的权值与偏置进行更新，训练神经网络模型。

其中，α表示学习率；∇w1、∇b1、∇w2、∇b2分别表示误差损失函数对w1、b1、w2、b2的偏导数：

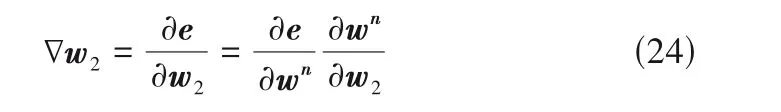
当混合模型的输出误差小于给定阈值时，停止训练。使用平均均方根误差(RMSE)、平均相对误差(MAPE)对模型的性能进行评价，各评价指标的定义如下：

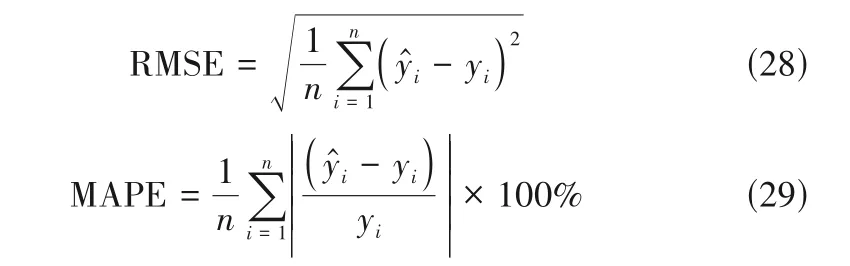
2 模拟结果与讨论

在本节中，基于第1节中所提出的模型框架，以某分解炉为研究对象，验证模型的准确性，并基于计算结果对分解炉内运行情况与动态特性进行简要分析。

2.1 工况介绍

对某5000 t/d 水泥生产线分解炉系统进行分析。分解炉部分参数如表1所示。

表1 分解炉参数Table 1 Parameters of calciner

计算使用的燃料特性参数如表2所示。

表2 燃料特性参数Table 2 Parameters of fuel characteristic

从DCS 系统中保存的历史数据中选取两组数据分别作为训练集和测试集，采样间隔为5 s。以2021 年7 月6 日的1500 条连续数据作为训练集，以2021 年7 月8 日的1000 条数据作为测试集，使用不同时间段采集得到的数据以更好地检验模型的泛化性能。

分解炉内固气停留时间比通常由炉型决定的，不同类型的分解炉固气停留时间比具有很大差异[45]。根据设计情况及实际运行经验，本研究对应分解炉的固体停留时间τs与气体停留时间τg分别约为10 s和7 s，因此分别取不同的固气停留时间比τsτg进行分析。

2.2 模型验证

为了验证模型的准确性，本文将混合模型计算结果与现场数据进行对比，从温度、NOx浓度等方面进行分析。

图4为固气停留时间比的设定对计算结果的影响，可以看出当固气停留时间比为1.3 时，温度的均方根误差达到最小值，且此时分解炉内的气体停留时间为7.80 s，固体停留时间为10.15 s，与实际运行情况较为符合。

图4 固气停留时间比的影响Fig.4 Effect of solid-gas residence time ratio

固气停留时间比取1.3 时，炉内某一时刻部分参数计算结果如表3所示。

表3 计算结果Table 3 Calculation result

混合模型的计算值与实际值较为接近，温度、压力以及主要气体浓度的相对误差均在10%以内。

温度以及NOx浓度的预测值与实际值随时间的变化情况如图5 所示，预测值与真实值有相近的变化趋势，温度与NOx浓度的均方根误差分别为4.06 K 和6.22 mg/m3，其误差分布情况如图6 所示。温度的计算误差大多小于5 K，而NOx浓度的误差基本分布在1～6 mg/m3之间。

图5 温度及NOx浓度的模型预测值与真实值对比Fig.5 Comparison of model predicted value and real value of temperature and NOx concentration

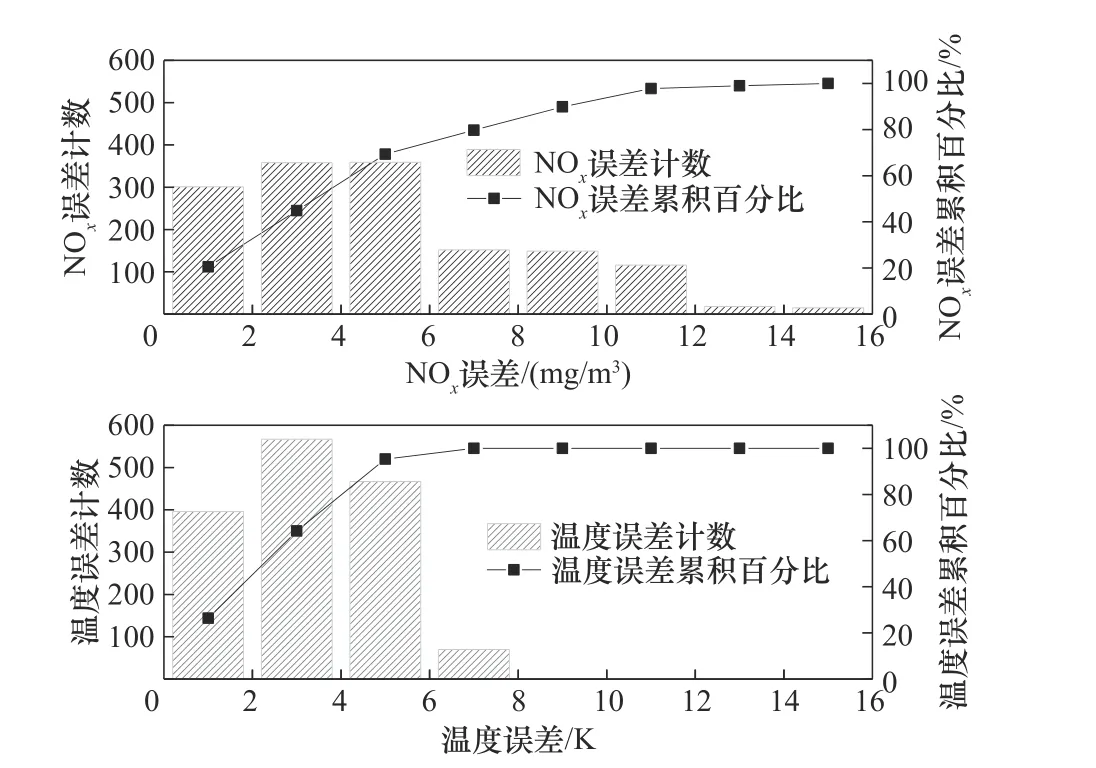
图6 计算误差分布Fig.6 Error distribution

产生误差的原因一方面是在机理建模时进行了较多的简化假设使得模型与实际情况产生偏离；模型中使用的化学反应常数为文献中给出的经验值，在实际应用时存在一定误差；另一方面利用数据驱动的方法拟合多相流动，在误差反向传播计算过程中进行了近似计算，产生了一定的截断误差，反向传播的误差值并不能完全真实反映使用神经网络模型进行流动计算产生的误差。此外，真实数据中包含有较多噪声和异常值，尽管已经对数据进行了滤波和异常值处理，但仍会对计算过程产生一定影响。

训练集与测试集中的误差对比如表4 所示，测试集中温度和NOx的均方根误差分别为6.72 K 和7.35 mg/m3，相对误差分别为0.50%与9.01%，该误差与训练集中的计算结果相差不大。由于模型融合了基于化学反应机理的先验知识，所以具有较好的泛化性能，在不同的运行工况下表现出相近的计算精度。

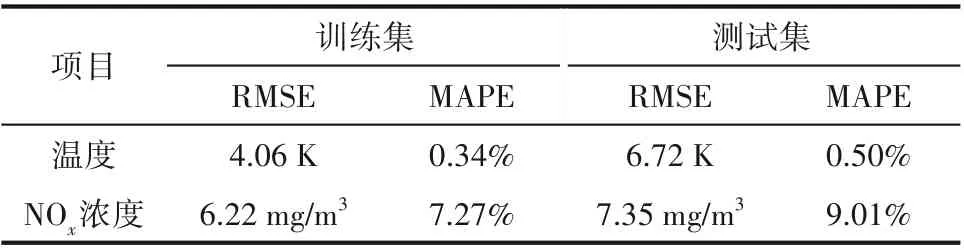
表4 训练集与测试集误差对比Table 4 Comparison of training error and test error

2.3 炉内参数分布

基于所建立的一维混合模型对分解炉内各项参数沿炉膛轴向的变化情况进行研究。

分解炉内各控制体内的温度、颗粒反应率以及气体组分的变化情况如图7 所示，分解炉锥部三次风口以下的部分平均温度约为1490 K，在该区域内有少量煤炭发生不完全燃烧，使得该区域温度仅略高于窑尾烟气温度(1430 K)。在控制体1 内，煤炭、生料以及三次风的加入使得分解炉内的温度开始升高，由于控制体1 内的气体的径向与切向流动比较剧烈，物料与气体混合充分，反应速率较快，控制体1内的平均温度可达1550 K左右。在焦炭与挥发分燃烧的同时进行着生料分解的吸热反应，因此炉内温度始终被控制在合理区间。分解炉缩口结构造成的气体喷腾效应能够加快局部的气体流速[40]，从而加强该区域内的气固反应速率，总体上各控制体内的平均温度仍然呈逐渐降低的趋势。沿流程方向燃烧反应与分解反应速率降低，炉内温度的变化幅度逐渐变小。

图7 模型预测值与真实值对比Fig.7 Comparison of model predicted value and real value

生料分解率与焦炭燃尽率的变化幅度在逐渐减小，一方面沿着炉膛轴向方向温度不断降低，使得焦炭燃烧和碳酸钙分解反应速率随之降低；另一方面随着反应的进行，反应面积随粒径不断减小，反应产物的生成也在一定程度上阻碍了反应的进行。另外，分解炉内轴向流速以及径向、切向流速都在逐渐降低，气固混合减弱，对固相的反应也会产生一定影响。分解率与燃尽率的变化趋势大致相似，分解炉出口处的焦炭燃尽率约为98%，与设计的燃尽值存在一定误差。分解炉出口碳酸钙分解率计算结果为96%，该结果与实际检测值相近。

分解炉内O2与NOx沿轴向的浓度变化趋势如图7 所示。由于底部少量煤炭的加入，分解炉锥部三次风口以下的控制体内煤炭不完全燃烧，O2含量小幅度降低，该区域的还原性气氛有利于烟气中NOx的还原。来自回转窑的烟气中NOx含量约为350 mg/m3，在锥部还原区经过自脱硝，烟气中的NOx浓度降为250 mg/m3。在控制体1 内，三次风的加入使得该区域O2含量升高，随着燃烧反应的进行沿炉膛方向O2浓度逐渐降低。在控制体1 内新加入的煤炭中的挥发分迅速析出，产生的焦炭以及还原性气体与NOx反应，使得控制体1 内的NOx浓度进一步降低。在随后的控制体内，NOx的生成速度逐渐高于还原速度，NOx含量开始升高。在分解炉尾部SNCR 反应区，喷入炉内的氨水与NOx发生还原反应，使得尾部区域的NOx含量显著降低，最终NOx的排放浓度约为70 mg/m3。

2.4 动态特性分析

基于所建立的分解炉运行过程模型，重点考虑给煤量、下料量、喷氨量以及高温风机转速的改变对分解炉出口温度以及NOx排放量的动态响应特性的影响。分解炉内生料下料量的变化范围一般为100～110 kg/s，喷煤量变化范围一般为3.8～4.6 kg/s，10%的阶跃变化对系统来说可能是最严峻的工作状态，因此本文为各操作变量设置了10%的固定阶跃，从而分析系统在严峻工况变动下的动态特性，获得系统在极端条件下的调节时间、超调量等，相关动态特性可以为分解炉控制系统的设计提供参考与依据。

2.4.1 给煤量阶跃变化 给煤量在t0时刻阶跃增加，此时分解炉出口温度T和NOx浓度的动态响应如图8 所示，图中t1和t2分别表示给煤量扰动后分解炉出口温度和NOx浓度再次达到稳态的时刻；T0和T1分别为初始状态下和重新达到稳态时对应的分解炉出口温度；N0和N1分别表示初始和重新稳态时对应的NOx浓度。给煤量阶跃增加后，炉内可燃碳量增加，燃烧释放热量使得温度升高，分解炉出口温度逐渐升高达到稳态值。给煤量增加后，一方面由于炉内温度升高，促进了NOx的反应，另一方面煤炭内的氮元素参与反应转换为NOx，使得出口处NOx含量升高并最终达到稳态值。NOx反应对于温度比较敏感，NOx会以相对温度更长的时间达到稳态，即t2＞t1。

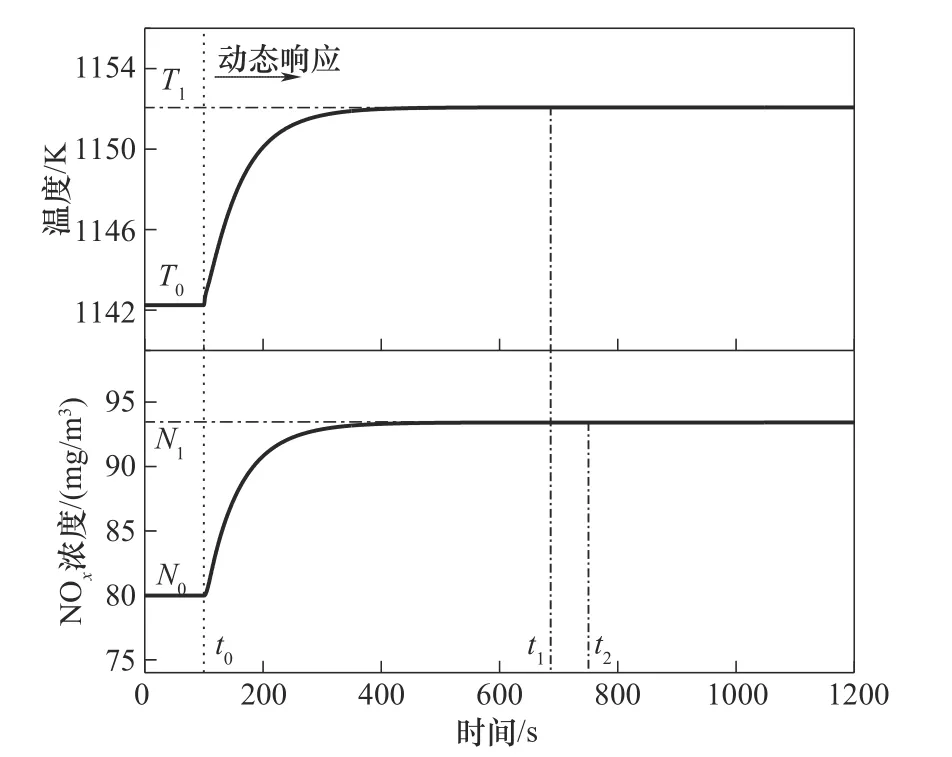
图8 给煤量阶跃变化Fig.8 Step change of coal feed

2.4.2 生料量阶跃变化 图9 为生料量阶跃增加10%时分解炉出口温度与出口NOx浓度的动态响应情况。生料量阶跃增加后，出口温度立即升高，之后开始逐渐降低，达到最低点后小幅回升并逐渐达到稳态值，稳态值低于初始值。由式(4)的能量守恒机理分析，高温生料的进入立即给炉内带来大量热量，式(4)中的值增加，炉内温度呈现瞬时的升高趋势。之后由于这部分生料与炉内高温烟气进行换热，生料温度不断升高，分解反应持续进行，吸热量增加，使得炉内温度逐渐降低并达到最小值。随着反应的进行，生料分解产生的大量气体使得烟气量增加，热容量随之增大，最低点后温度产生了较小的提升。

图9 生料量阶跃变化Fig.9 Step change of limestone

由于喷煤量及窑尾烟气量等其他条件没有改变，NOx浓度的变化情况便仅与温度有关。出口NOx的动态响应特性与温度相似，NOx浓度先迅速增加，之后逐渐下降到最低点并缓慢上升至新的稳态值。2.4.3 喷氨量阶跃变化 喷氨量阶跃增加10%，此时分解炉出口温度与NOx浓度动态响应如图10 所示。喷氨量增加后，由于喷入炉内的氨水蒸发吸收热量，会使炉内温度略有下降，由于SNCR 反应区布置在分解炉尾部，距离分解炉出口较近，并且氨水蒸发吸热的速度较快，分解炉出口温度在很短时间内便达到新的稳态值。

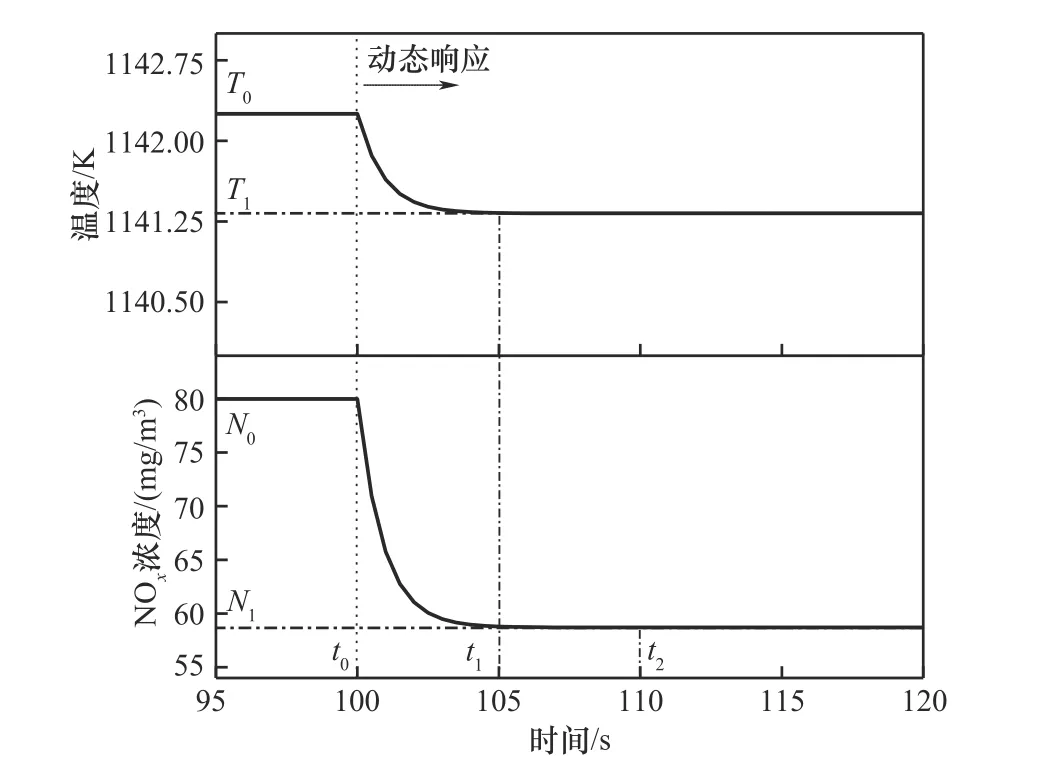
图10 喷氨量阶跃变化Fig.10 Step change of ammonia injection

氨水中的大量NH3与炉内的NOx发生还原反应，使得出口处的NOx含量快速降低，并逐渐趋于稳定。

2.4.4 高温风机转速阶跃变化 高温风机转速阶跃增加时，对应的温度与NOx浓度动态响应如图11所示。

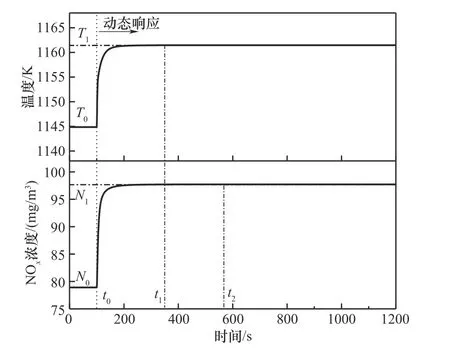
图11 高温风机转速阶跃变化Fig.11 Step change of high temperature fan speed

转速提高后，系统引风量增加，来自回转窑的高温烟气量升高，给炉内带去大量热量，使得分解炉内温度快速升高。烟气量的增加使得分解炉内总的热容量变大，温度变化幅度逐渐变小，最终温度逐渐趋于稳定值T1。

高温风机转速变化对NOx浓度的影响主要体现在两个方面：一方面，引风量增加，随回转窑烟气进入分解炉的初始NOx含量提高；另一方面，分解炉内温度的升高，使得NOx的生成量随之增加。因此高温风机转速增加后，NOx含量随之升高，并逐渐趋于稳定。

3 结 论

本工作以水泥分解炉为研究对象，提出一种化学反应机理与神经网络相结合的混合建模策略，使用差分法和梯度下降法对神经网络进行训练，建立分解炉一维动态混合模型并得到以下结论。

（1）结合工业数据对这种建模方法的可行性进行验证，其出口温度与NOx浓度的均方根误差分别为4.06 K 和6.22 mg/m3，相对误差分别为0.34%和7.27%。模型在测试集上的均方根误差分别为6.72 K和7.35 mg/m3，与训练集中的计算误差相差不大，具有较强的泛化性能，可以满足工程计算的需要。

（2）基于所建立的模型对炉内参数稳态特性进行分析，各参数分布情况与实际情况较为符合。分解炉内温度分布呈现先升高后降低的趋势，温度在三次风口以上区域达到最高点；煤炭燃尽率与生料分解率沿烟气流动方向不断提高且增加幅度逐渐变缓。底部还原区的设置使得烟气实现了自脱硝，分解炉尾部SNCR 喷氨系统的设置也使得出口NOx含量大幅降低。

（3）基于所建立的模型对喷煤量等参数阶跃变化条件下分解炉出口温度以及NOx浓度的动态响应特性进行研究。在不同参数的阶跃仿真下，呈现出不同的动态响应特性；NOx与温度具有相似的变化规律，但NOx的响应时间比温度的响应时间更长。所获得的阶跃仿真数据及动态特性分析结果可为被控对象的参数辨识以及模型控制器的设计提供依据。

符 号 说 明

Ci——气体i浓度，kmol/m3

Cp——比热容，kJ/(kg·K)

DL——炉膛直径，m

dc——焦炭直径，m

F——质量流率，kg/s

Gn——生成速率，kg/s

H——炉膛高度，m

M——摩尔质量，g/mol

m——质量，kg

P——压强，Pa

Q——热量，kJ

R——气体常数，J/(kg·K)

Rn——消耗速率，kg/s

T——温度，K

ξ——尺寸修正系数

ρ——密度，kg/m3

上角标

n——控制体

下角标

g——气体

i——气体组分

k——时刻

p——颗粒