(1+1)维混合KdV方程的通用F-展开和精确解
陈 南,张雪健
(厦门工学院计算机与人工智能学院,福建厦门 361021)
0 引言
非线性偏微分方程的求解问题,一直以来受到广大学者的关注.目前,已有很多方法对方程求解,例如:齐次平衡法[1]、达布变换法[2]、Painlevé分析法[3]、G′/G函数展开法、F-展开法等.文献[4]中,把F-展开法推广到一般椭圆方程
F′2(ξ)=c0+c1F(ξ)+c2F2(ξ)+c3F3(ξ)+c4F4(ξ)
(1)
式(1)中ci(i=0,1,...,4)为参数,并给出了一般椭圆方程(1)的由系数之间的联系所确定的12种Jacobi椭圆函数解,并借助这些解把F-展开法推广到一般椭圆方程的情形,即提出了通用F-展开法.
(1+1)维混合KdV方程
ut+a0ux+a1uux+a2u2ux+βuxxx=0
(2)
它则是描述非线性晶体传播的方程.目前对(1+1)维混合KdV方程的研究文献比较多,文献[5]用F-展开法对该方程进行了求解,文献[6]中使用G'/G展开法和G'/G扩展法对方程进行求解.本文选择了文献[4]提出的通用F-展开法对该方程进行求解.
1 应用通用F-展开法
作行波变换,u(x,t)=u(ξ),ξ=k(x-ct),其中k和c分别为波数和波速,则方程(2)变为
-cu'+α0u'+α1uu'+α2u2u'+k2βu'''=0
(3)
假设方程(3)具有如下形式的解,
(4)
式(4)中n,ai(i=0,1,...,n)为待定常数,且F(ξ)满足一般椭圆方程(1).利用齐次平衡原则,可得n=1.故式(3)的解为
u(ξ)=a0+a1F(ξ)
(5)
式(5)中F=F(ξ)满足式(1).由式(1)可得
(6)
利用式(1)、式(6),由式(5)可得
u′=a1F′
(7)
u‴=a1(c2F′+3c3FF′+6c4F2F′)
(8)
将式(5)、式(7)、式(8)代入式(3),并令FiF′(i=0,1,2)的系数为零,得到关于a0,a1,k,c的方程组
(9)
(10)
(11)
解该方程组得
(12)
式(12)中ε=±1.
2 (1+1)维混合KdV方程的精确解
利用文献[4]中给出得一般椭圆方程得Jacobi椭圆函数解,得到方程(2)的如下三种情形的解为:
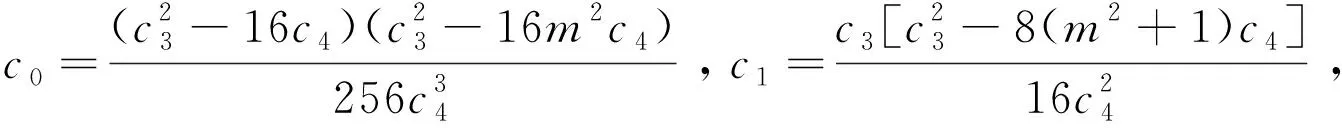
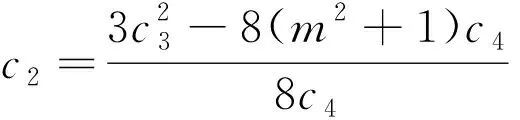
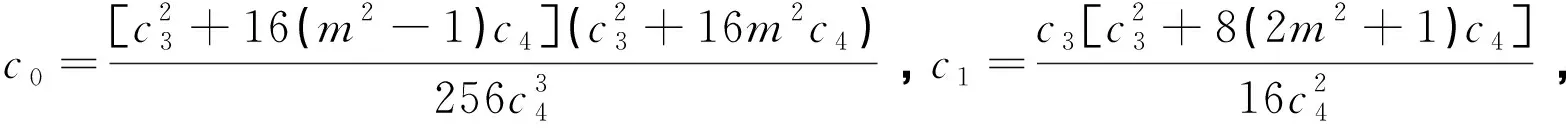
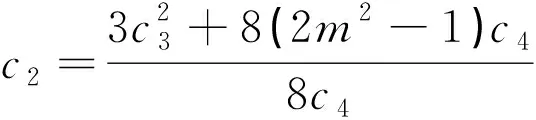

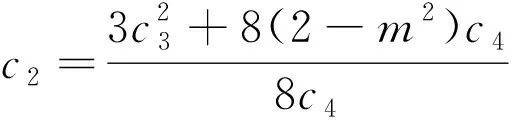
其中,m(0 求解非线性偏微分方程,一直是一个重要的问题.本文利用文献[4]中提出的通用F-展开法对(1+1)维混合KdV方程进行分析求解,得到了12种Jacibi椭圆函数解,丰富了(1+1)维混合KdV方程的解系.后续,可推广至其他方程.3 结论

