优化人像视频编码比特分配算法

杨 栩

(成都师范学院物理与工程技术学院，四川成都 611130)

0 引言

随着视频会议系统的逐步普及，其作为最重要的视频编码应用之一越发受到工业界和学术界的重视.人像视频是视频会议最主要的应用场景，在带宽限制条件下的视频数据传输面临着诸多挑战，码率控制[1]在对实时性要求比较高的低延时视频会议系统中占据着举足轻重的地位.新一代视频编码标准VVC(Versatile Video Coding)采用R-λ模型[2-3]，码率控制算法根据带宽、缓冲器大小确定各个GOP(Group of Pictures)、帧、编码树单元CTU(Coding Tree Unit)的目标比特数，然后通过R-λ-QP模型计算编码帧的量化参数QP(Quantization Parameter)进行编码.编码失真主要来自量化过程，量化步长的大小和失真大小成正比关系；所以，独立率失真优化下的拉格朗日乘子λ和量化步长Δ间存在密切关系，在高码率下，他们之间的关系表达式为

λ=c·Δ2

(1)

其中，c为常数，量化步长和量化参数间存在函数映射关系.文献[4]证明了常数c的取值为0.85.实际上，拉格朗日乘子不仅与量化参数有关，还与多个编码参数有关，比如文献[5]指出拉格朗日乘子还与信源方差相关.所以直接通过量化参数建立的QP-λ关系还不是最优表达式.文献[6]提出了基于全局拉格朗日乘子的全局率失真优化，认为整个视频序列应该共享同一个全局拉格朗日乘子并获得了非常大的率失真性能提升；文献[7]解释了独立RDO和依赖RDO所对应的拉格朗日乘子的区别，说明考虑时域依赖关系的全局拉格朗日乘子能够实现全局优化.为了进一步提升VVC码率控制精度和率失真性能，本文应用递归泰勒展开法[8]计算全局拉格朗日乘子并应用到VTM12.0参考软件CTU(Coding Tree Unit)级码率控制，取得了较大的性能提升.

1 VVC比特分配算法

比特分配是码率控制算法中最为关键环节，优化比特分配是提高编码性能和码率控制精度的前提.VTM采用分层比特分配结构，在GOP层[9]、帧层、CTU层分别进行比特分配，越往下，码率分配越准确.VTM在各个层次上平均分配目标码率，为了逐步消除已编码单元产生的码率控制误差，通过滑动窗口来平滑码率波动，通过下列式子实现分层码率分配，即

(2)

(3)

(4)

(5)

其中，Rtar为目标码率，FR为帧率，Rpic为平均每帧的比特数，Tgop、Tpic、Tctu分别为分配给待编码GOP、编码帧、编码单元的目标比特数；SW是平滑比特分配的滑动窗，Ncoded、Rcoded、Ngop、Rcodedgop、ωpic、ωctu、∑notcodedpicgopωpic、∑notcodedctupicωctu分别为已编码帧数、已消耗比特、GOP帧数、GOP内已编码帧数、编码帧所占权重、编码单元所占权重、未编码帧所占权重之和、帧内未编码CTU权重之和.

1.1 低延时P帧配置编码结构及权重系数

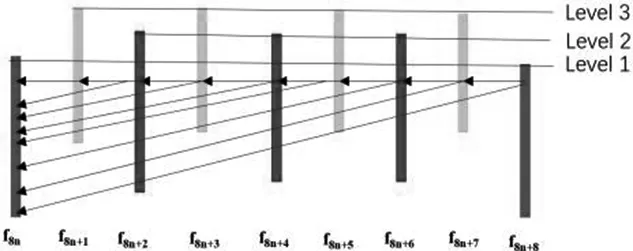
图1 VTM12.0参考代码在 LDP下GOP结构Fig.1 GOP structure of vtm12.0 under LDP

VVC在LDP(Low Delay P)配置下每个GOP包含8帧图像，编码树单元CTU大小为128*128，一个GOP中各帧分别属于不同的层次，分别为关键帧所在的第一层Level1，偶数帧所在的第二层Level2，奇数帧所在的第三层Level3.每帧都有4个参考帧，分别为时域最近邻的前一帧以及已编码的最近邻三个关键帧，图1给出了VTM12.0在LDP下POC(picture order count)序号从f8n到f8n+8的一个GOP的编码结构.

对于CTU级的码率分配，文献[2]提出编码器根据编码单元的权重占比来预分配，CTU级根据R-λ模型来计算权重系数，当前编码CTU的计算参数由上一帧同位置CTU相关参数确定.假设编码单元所在编码帧被分配到的比特数为Rpic.每个编码单元独立求解最优编码参数问题.即

(6)

D和R分别为编码失真和编码比特消耗，λi为第i个编码单元对应的拉格朗日乘子，Ji为第i个编码单元的率失真代价，编码器通过最小率失真代价Ji来进行编码模式选择，编码模式主要指帧内及帧间预测模式.

可得CTU级R-λ模型，即

D=C·R-k

(7)

其中，C和K为模型参数.

(8)

式(8)中每个编码单元有Ri=bppi·Ni，其中Ri、bppi、Ni分别为编码单元目标比特数、每像素所占比特以及像素数，λi为编码单元的拉格朗日乘子，其初始值为帧级拉格朗日乘子.所以编码单元的比特分配关键在于确定权重系数ωctu与式(10)中相关参数的关系，即

(9)

(10)

ωctuj为第j个编码单元权重系数，Rpic为当前帧分配的比特数，ωctui、λi分别为当前编码单元的权重系数和拉格朗日乘子，ri为第i个编码单元分配的比特数.

1.2 优化比特分配

根据前文可知，为了简化编码问题，降低复杂度，将各编码单元看作在时域上相互独立的个体，各编码单元使用的相关参数在时域上互不影响，通过拉格朗日乘子法将约束性优化问题转换为非约束性优化问题.虽然这样简化了问题，但是也人为切断了编码单元间在时域上的相关性，这样的优化只是局部优化，编码性能的提升需要考虑编码单元时域、空域相关性.

文献[8]提出了一种基于递归泰勒展开法RTE(Recursive Taylor Expansion)的数学求解方法来求解全局拉格朗日乘子.本文用RTE来求解帧内CTU共享的全局拉格朗日乘子，并用于优化CTU级的比特分配.

根据上文的R-λ模型，可得帧级分配的比特与各编码单元分配的比特关系为

(11)

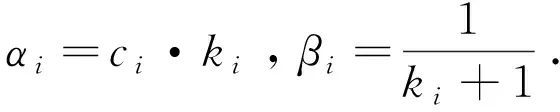
(12)

截断式(12)4阶及其以上项，通过盛金公式计算出全局拉格朗日乘子λg并应用与实际编码.实际编码实验中经过4次递归就能达到递归结束条件.

将λg应用到更新比特分配公式中.通过改变编码单元的权重占比来优化比特分配，这里的权重占比不仅跟全局拉格朗日乘子有关，还与编码过程中的更新参数αi、βi有关.

(13)

(14)

(14)式中ri'为第i个编码单元优化分配后的比特数.

1.3 算法流程

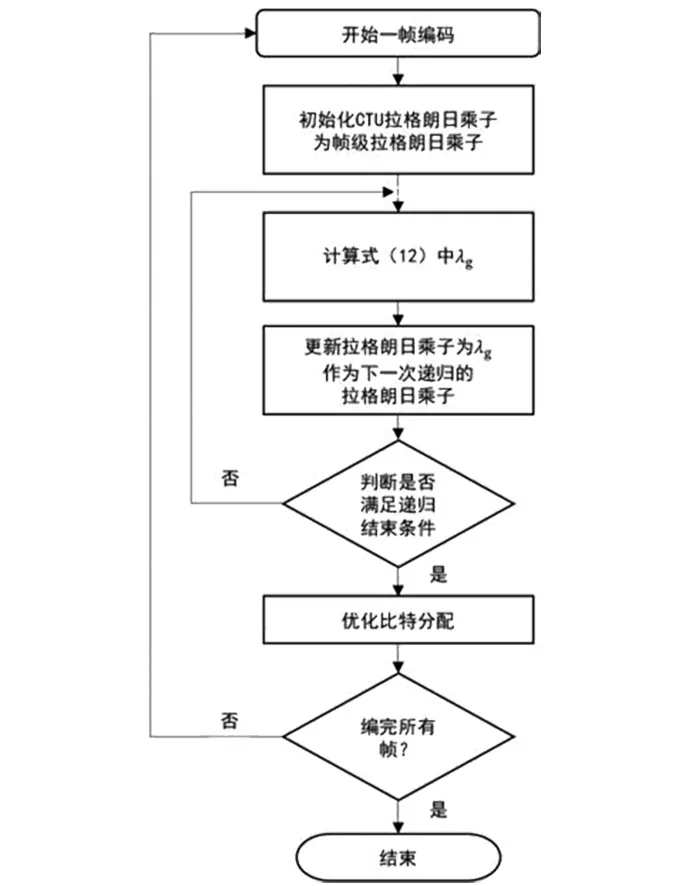
图2 优化比特分配算法流程图Fig.2 Flow chart of bit optimization algorithm

在实际编码过程中，需要将递归泰勒展开法所求全局拉格朗日乘子应用到比特优化分配中，初始值由帧级拉格朗日乘子代替.具体流程如图2所示.

2 实验分析

为验证本文方法有效性，将算法应用于CTU级比特优化分配并集成到VVC/H.266参考软件VTM12.0的码率控制算法中，编码器配置为LDP，实验选用提案JCTVC-L1100[10]建议的ClassE中的全部3个人像视频序列，标准测试序列特征如表1所示.

表1 标准测试序列特征Tab.1 Characteristics of standard test sequence

实验计算机配置为Inter(R)Core(TM)i7-7700K CPU@4.2 GHz，内存为16 GB，基于X64的处理器，64位Windows10专业版操作系统.

参考软件VTM12.0在不开启码率控制的情况下，分别用QP值22、27、32、37去编码每个测试序列，所得的4个码率值作为码率控制实验的目标码率.实验通过对比VTM自带的码率控制算法和本文提出的算法，分别记为VTM_RC和RTE_RC.编码器配置文件为encoder_lowdelay_P_vtm.cfg.

2.1 率失真性能对比

码率控制算法是在目标码率的限定下，尽可能降低失真，而且编码时间是衡量算法复杂度的重要参数.所以，码率控制算法的好坏，不仅要看码率控制的精度，还要看编码时间和率失真性能，如表2所示.本实验以固定QP为22、27、32、37不开启码率控制的VTM12.0为基准，将基准码率作为实验的目标码率，分别计算VTM12.0自带的码率控制算法(VTM_RC)以及基于递归泰勒展开法的码率控制算法(RTE_RC)相较于基准的BD-rate.在相同比较基准下，测试算法的BD-rate越小，其性能越好.表2列出了2种算法相较于VTM12.0基准BD-rate，可以看出，RTE_RC算法相较于基准的BD-rate为-1.6%，远好于VTM-RC算法相较于基准的4.97%.本文算法的率失真性能都得到了不同程度的提升.表2中△R表示码率控制精度也即实际编码码率和目标码率的相对误差，△T表示编码时间节省.这两个性能指标将在后文详细说明.

表3给出了RTE_RC算法总体平均PSNR为40.03 dB，相较于VTM_RC的39.79 dB增长了0.24 dB.RTE_RC算法率失真性能有了很大提高.为了更直观观察率失真性能提升情况，选取部分测试序列来分析.图3给出了2个测试序列”Johnny”、”KristenAndSara”在LDP下不同算法的率失真曲线对比图.可以很清晰看出本文算法RTE_RC率失真性能更好.

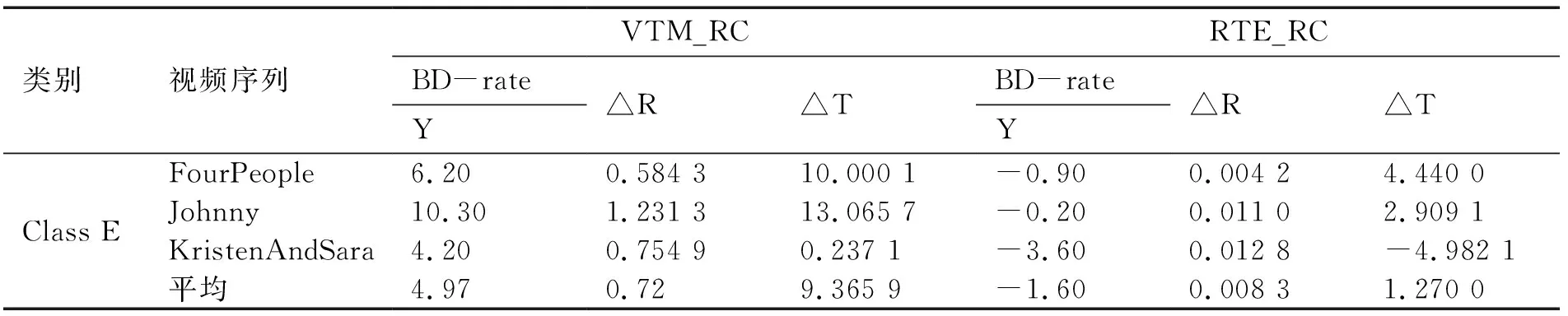
表2 优化比特分配算法测试结果(%)Tab.2 test results of bit optimal allocation algorithm

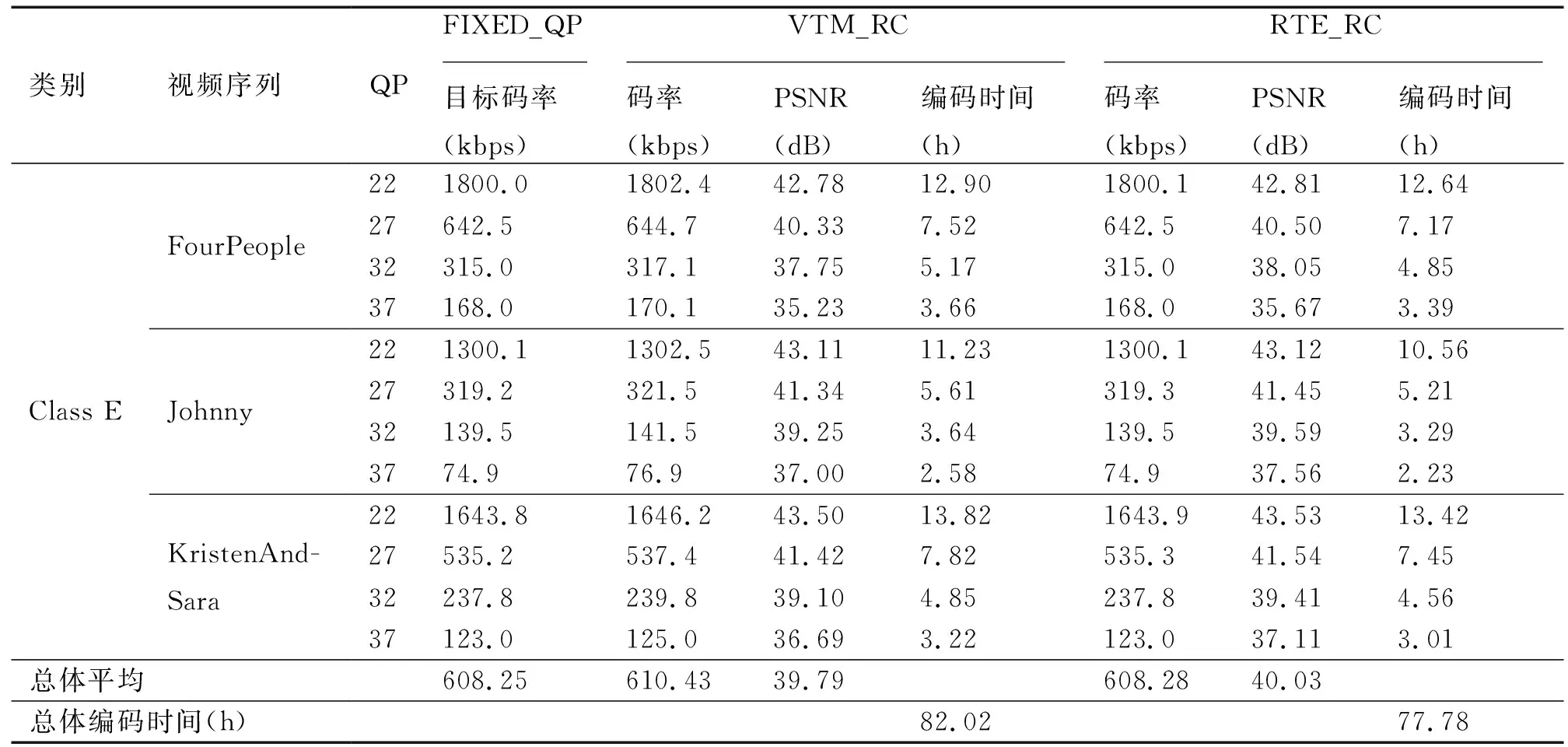
表3 不同算法码率/PSNR/编码时间对比Tab.3 bit rate / PSNR / encoding time of video sequence under different algorithms

图3 测试序列Kristen and Sara/Johnny在不同算法下率失真曲线对比图Fig.3 rate distortion performance comparison in the test sequence Kristen and Sara / Johnny

可以看出本文算法RTE_RC率失真性能相较于参考代码码率控制算法VTM_RC率失真性能有了较大提升.

2.2 码率控制精度对比

码率控制精度是码率控制算法中的核心，最好的码率控制结果是分多少比特用多少比特.

通过计算实际编码码率和目标码率的误差来描述码率控制精度，计算式为

(15)

上式中，Rtar表示目标码率，Ract表示实际编码码率.△R越小，表明码率控制精度越好.表2列出了每个测试序列在4个目标码率下的平均码率的相对误差，数据显示VTM_RC在LDP下对全部测试序列的平均码率相对误差为0.72%；而本文算法RTE_RC在LDP下对全部测试序列的平均码率相对误差仅为0.008 3%.码率控制精度得到了极大提高.

2.3 编码时间对比

编码时间是衡量算法复杂度的重要指标，正如视频编码标准的更新换代，虽然提升了压缩率，但是却是以牺牲更大的编码时间作为代价.本文算法(RTE_RC)和参考软件码率控制算法(VTM_RC)编码人像视频测试序列所用绝对时间如表3所示.可以看出，本文所提算法总共花费时间77.78 h，低于VTM_RC的82.02 h，编码时间降低5.17%.

表2的△T表示以VTM12.0不开启码率控制固定QP的编码时间为基准，算法VTM_RC和RTE_RC相较于基准的时间变化率，△T为正数表明编码时间相较于基准时间有增加，反之，△T为负数表明编码时间相较于基准时间有降低.计算式为

(16)

上式中Tqp表示用固定QP编码该视频序列所花时间，Trte表示用RTE_RC算法编码该视频序列所花时间.通过表2可以看出，相比VVC参考代码码率控制算法，本文算法在所有视频序列上编码时间都有降低.这主要是因为优化比特分配后，给帧内变化较大CTU分配较多比特，变换平缓CTU分配较少比特，长远来看，这间接提升了编码性能，会增加选择skip模式的几率，这样会节省编码时间.

3 结语

随着低延时实时视频会议系统的普及，视频会议系统对低延时要求越来越高，这对码率控制提出了更高要求，如何进一步提高码率控制精度和率失真性能，同时降低编码时间是码率控制面临的主要问题.本文通过递归泰勒展开法计算每帧的全局拉格朗日乘子，并应用于更新CTU权重占比计算，以此来优化人像视频的比特分配.实验证明，本文算法能较大提高码率控制精度及率失真性能，而且编码复杂度有所降低.