基于Galerkin法的新型波形钢腹板箱梁桥动力特性研究
冀 伟,温凯康,罗 奎
(1.兰州交通大学 土木工程学院,甘肃 兰州 730070;2.湖南大学 土木工程学院,湖南 长沙 410082)
新型波形钢腹板组合箱梁桥(底板为钢材)可使钢材和混凝土材料的性能得到充分发挥,合理地改善结构的受力性能,有效避免混凝土底板易开裂的弊病。将混凝土底板换成钢底板可大幅减小箱梁自重,提高跨越能力,便于现场运输及架设,提高桥梁的使用寿命。
国内外已有学者对波形钢腹板组合梁桥的动力特性进行了研究,Feng等考虑转动惯量和界面滑移的影响,推导了波形钢腹板组合箱梁桥自振频率的计算公式,并利用有限元结果对解析解的正确性进行了验证;Moon等采用数值模拟和试验研究相结合的方法对波形钢腹板组合梁的自振频率进行了研究,为该类桥型自振特性分析提供了一种简化分析方法;Kashefi等通过有限元模拟获取了薄壁直线箱梁和曲线箱梁的自振频率和阻尼比,并将有限元结果与试验实测结果进行对比,验证了所提数值模拟方法的有效性;Jiang等研究发现界面滑移对波形钢腹板组合梁的自振频率的影响高达13.7%;Yang等基于能量变分原理推导了波形钢腹板组合槽梁自振频率的计算公式,并利用有限元模型的计算结果对公式的正确性进行了验证;Zhang等提出了一种分析波形钢腹板组合梁动力特性的方法,并利用有限元方法与欧拉梁理论进行验证,结果表明,跨宽比越小,自振频率越大,剪力滞效应越明显;Shi等利用能量变分法推导了变截面波形钢腹板组合箱梁的单元刚度矩阵和单元质量矩阵,通过有限梁段单元法分析了变截面波形钢腹板组合箱梁的动力特性,结果表明,自振频率随着梁的变截面系数增大而增大,随着宽跨比的增大而减小;冀伟等考虑剪切剪滞双重效应的影响,运用Hamilton原理推导了简支梁的自振频率计算公式,随后又根据三弯矩方程推导了连续梁自振频率的计算公式,并利用试验实测结果和有限元结果对计算公式的正确性进行了验证;项贻强等采用两种不同的刚度法研究了滑移和体外预应力对钢-混组合梁自振频率的影响;王力等利用应力等效原则,研究了温度对新型波形钢腹板组合箱梁桥动力特性的影响,结果表明,时变温度会使新型波形钢腹板组合箱梁桥的频率发生显著改变;郑尚敏等利用试验研究和有限元分析的方法,研究了体外预应力对单箱双室箱梁自振频率的影响;罗奎等考虑全截面剪切变形效应,运用势能驻值原理推导了波形钢腹板组合箱梁桥的单元刚度矩阵,并利用MATLAB编制了自振特性和挠度的求解程序,为该桥型自振频率和挠度分析提供了一种简单的分析方法;马驰等考虑剪切剪滞双重效应,利用子空间迭代法对波形钢腹板组合箱梁桥的动力特性进行了研究,结果表明,剪切剪滞效应使自振频率有所减小,且对高阶频率影响较大。
分析现有文献可知,目前国内外学者对该类桥型动力特性的研究主要集中在底板为混凝土的波形钢腹板组合梁桥,而对底板为钢材的新型波形钢腹板组合箱梁桥的静力和动力性能仅进行了初步的探索。因此,本文运用Hamilton原理和Galerkin法,综合考虑波形钢腹板的剪切变形效应和箱梁的剪力滞效应,推导出新型波形钢腹板组合箱梁桥弯曲振动频率的计算公式,并通过试验实测结果、ANSYS有限元结果对本文所提方法的正确性进行验证。
1 自由振动方程的建立
1.1 基本假定
根据新型波形钢腹板组合箱梁的特点,做出以下3点假设:1)因波形钢腹板轴向刚度非常小,在计算中往往可以只考虑剪切刚度,在运用能量变分法时,假设腹板承受全部的剪力;2)忽略梁的扭转变形,且波形钢腹板与混凝土顶板交界面不产生相对滑移;3)新型波形钢腹板组合箱梁始终处于弹性工作范围内。
新型波形钢腹板组合箱梁的截面尺寸如图1所示,其中,2b
为钢底板的宽度,2b
为内顶板的宽度,b
为混凝土悬臂板的宽度,h
、h
分别为箱梁截面形心轴至钢底板中心和混凝土顶板中心的距离。
图1 新型波形钢腹板组合箱梁的截面尺寸Fig. 1 Sectional dimensions of new type composite box girder with corrugated steel webs
由于剪力滞效应的影响,箱梁发生自由振动时,上下翼缘的挠度不再符合平截面假定,需引入两个广义位移函数,即竖向位移函数ω与纵向位移函数U
:

u
(x
,t
)为翘曲位移函数的位移幅值;φ
(x
,t
)为弯曲变形引起的角位移;t
为时间;f
(y
)为翘曲位移函数,f
(y
)的表达式如式(3)~(5)所示:
d
为满足全截面的轴力自平衡附加轴力位移,表达式如式(6)所示: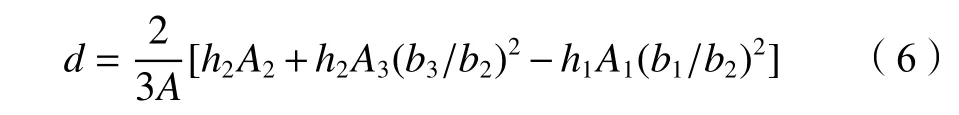
A
、A
、A
分别为钢底板、混凝土内顶板及混凝土悬臂板的截面面积;A
为顶板和底板截面的总面积,A
=A
+A
+A
。1.2 控制微分方程和自然边界条件
由式(3)和(4)可知,顶板的应变能V
表达式如式(7)所示:
E
、G
分别为混凝土的弹性模量和剪切模量;ε为 混凝土顶板的正应变; γ为剪切应变;I
为混凝土顶板对箱梁截面形心轴的惯性矩,I
=A
h
,其中,A
为顶板混凝土的截面面积;l
为桥梁的计算跨径;常数C
、C
、C
可分别通过式(8)~(10)得到:
正应变和剪切应变的计算如式(11)~(12)所示:

V
表达式如式(13)所示:
E
、G
分别为钢材的弹性模量和剪切模量; ε为钢底板的正应变; γ为钢底板的剪切应变;I
为钢底板对箱梁截面形心轴的惯性矩,I
=A
h
;常数B
、B
、B
可分别由式(14)~(16)得到:
正应变和剪切应变的计算如式(17)~(18)所示:

V
表达式如式(19)所示:
令
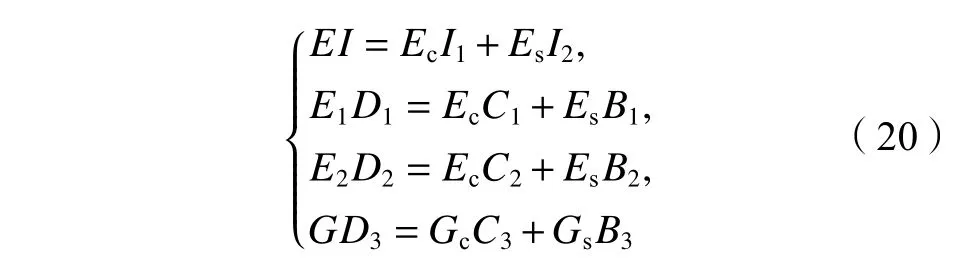
将式(20)代入式(19)中,可得新型波形钢腹板组合箱梁桥混凝土顶板和钢底板总应变能的表达式,如式(21)所示:

V
如式(22)所示:
A
为波形钢腹板的截面面积。总势能由顶板、钢底板和波形钢腹板3部分组成,由式(21)和(22)可得总势能V
: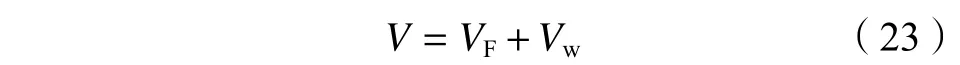
T
可用式(24)表示:
m
为新型波形钢腹板组合箱梁桥的单位长度质量,表达式为:
式中,ρ和ρ分别为混凝土的密度和钢材的密度。根据Hamilton原理:

将式(23)和(24)代入式(26)中,运用能量变分法可以得到控制微分方程,如式(27)~(29)所示:
自然边界条件如式(30)~(32)所示:
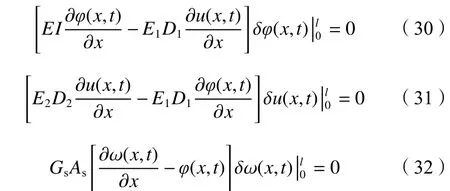
1.3 自由振动方程的解
将式(27)和(28)代入式(29)中,进行化简整理,得到简化式(33):

为求解式(33),假设新型波形钢腹板组合箱梁桥自由振动时的竖向位移函数ω为:

W
(x
)为新型波形钢腹板组合箱梁桥的竖向位移,ω、θ分别为自由振动时的圆频率和初始相位角。将式(34)代入式(33)中,可得:

利用Galerkin法简化式(35)的计算过程,对于新型波形钢腹板组合简支箱梁桥,可设:

A
为振型函数的振幅。权函数W
的表达形式设为:
将式(36)代入式(35)中,可以得到余量为:

由Galerkin法:
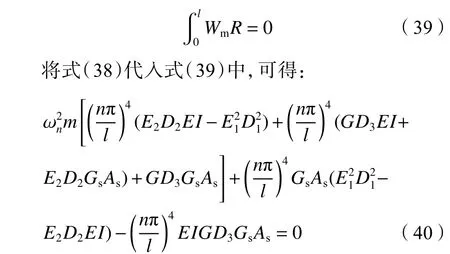


式中,分子的第2项和分母的第3项为剪力滞影响系数,分母的第2项为剪切变形影响系数,分母的第4项为剪切变形和剪力滞的共同影响系数。
由式(41)可以得到弯曲振动频率f
的表达式为:
2 算例验证
2.1 实桥验证
选取甘肃兰州景中高速机场连接线主匝道的一座新型波形钢腹板组合箱梁桥进行动力特性试验,该桥计算跨径29.22 m,截面为4箱单室,单箱截面尺寸如图2所示。波形钢腹板的波高为20.0 cm,厚度为1.2 cm,钢底板厚度为1.6 cm;波形钢腹板与钢底板的弹性模量均为2.1×10MPa,密度为7.8×10kg/m,混凝土的弹性模量为3.5×10MPa,密度为2.5×10kg/m。

图2 单箱截面尺寸Fig. 2 Sectional dimensions of a single box
利用ANSYS有限元软件建立新型波形钢腹板组合箱梁的3维有限元模型,混凝土顶板采用SOLID45单元进行模拟,横隔板、钢底板和波形钢腹板采用SHELL63单元进行模拟,建立的简支梁有限元模型如图3所示。

图3 简支梁的有限元模型Fig. 3 Finite element model of simply supported girder
利用文献[19]的试验实测结果对本文的理论结果进行验证。采用本文推导的计算公式求解该桥的前5阶弯曲振动频率,并将计算结果与ANSYS有限元结果、实测结果及理论计算值进行对比,结果如表1所示。
表1 不同方法所求的弯曲振动频率对比
Tab. 1 Comparison of bending vibration frequencies obtained by different methods
Hz频率阶数 本文值 有限元值[19] 理论计算值[19] 实测值[19]1 3.692 3.621 3.634 3.762 2 12.807 12.735 12.612 12.379 3 24.261 24.360 23.879 24.531 4 36.398 36.973 35.765 —5 48.657 49.061 47.685 —
从表1可以看出,本文推导的弯曲振动频率公式计算结果与ANSYS有限元结果、实测结果及理论计算值吻合良好,验证了本文所推导频率计算公式的正确性。
2.2 试验梁验证
选取文献[19]中的模型梁进行分析。该模型梁计算跨径8 m,顶板采用C50混凝土,波形钢腹板厚度为3 mm,波高40 mm,钢底板厚度为5 mm,所用钢材型号均为Q235,泊松比v
=0.3,弹性模量E
=206 GPa,模型梁截面尺寸如图4所示。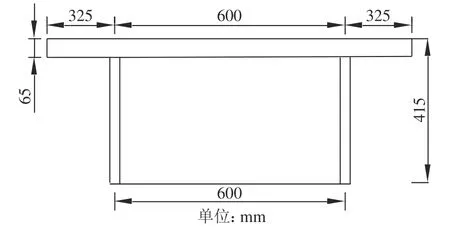
图4 模型梁截面尺寸Fig. 4 Sectional dimensions of the model girder
采用本文推导的方法,计算该模型梁的前5阶弯曲振动频率,并将计算结果与文献[19]中的ANSYS有限元结果和模型梁实测结果进行对比,结果如表2所示。
表2 3种方法所求的弯曲振动频率对比
Tab. 2 Comparison of bending vibration frequencies obtained by the three methods
注:=|(有限元值−本文值)/本文值|×100%, =|(实测值−本文值)/本文值|×100%。
频率阶数 频率/ Hz e1 e2本文值 有限元值[19] 实测值[19]1 13.844 14.070 13.650 1.63 1.40 2 48.169 47.628 44.044 5.06 8.56 399.068107.782 — 8.80—4153.199152.054 — 0.75—5 208.911183.049 — 12.38—
从表2可以看出:利用本文公式计算的第1阶弯曲振动频率与文献[19]中模型梁实测结果和ANSYS有限元结果误差分别为1.63%、1.40%;第2阶弯曲振动频率与文献[19]中模型梁实测结果和ANSYS有限元结果误差分别为5.06%、8.56%,进一步验证了本文所提方法的正确性。
3 参数分析
3.1 高跨比对弯曲振动频率的影响
为研究高跨比对新型波形钢腹板组合箱梁桥弯曲振动频率的影响,对箱梁高度分别取值为1.1、1.5(实桥)、1.9、2.3和2.7 m,其他条件保持不变,利用本文公式计算前5阶弯曲振动频率,结果如图5所示。

图5 高跨比对弯曲振动频率的影响Fig. 5 Effect of height-span ratios on bending vibration frequencies
从图5可以看出,弯曲振动频率随高跨比的增大而增大。当高跨比小于0.05时,弯曲振动频率的增幅较为平缓;当高跨比大于0.05时,弯曲振动频率的增幅较为显著。
3.2 宽跨比对弯曲振动频率的影响
为研究宽跨比对新型波形钢腹板组合箱梁桥弯曲振动频率的影响,对内顶板宽度分别取值为1.85、2.25、2.65(实桥)、3.05和3.45 m,其他条件保持不变,利用本文公式计算前5阶弯曲振动频率,结果如图6所示。

图6 宽跨比对弯曲振动频率的影响Fig. 6 Effect of width-span ratios on bending vibration frequencies
从图6可以看出,弯曲振动频率随宽跨比的增大而略有增大,但整体增幅不明显。故宽跨比对新型波形钢腹板组合箱梁桥弯曲振动频率产生的影响较小。
3.3 波形钢腹板厚度对弯曲振动频率的影响
为研究波形钢腹板的厚度对新型波形钢腹板组合箱梁桥弯曲振动频率的影响,对波形钢腹板的厚度分别取值为6、8、10和12 mm,其他条件保持不变,利用本文公式计算前5阶弯曲振动频率,结果如图7所示。

图7 波形钢腹板厚度对弯曲振动频率的影响Fig. 7 Effect of thickness of corrugated steel webs on bending vibration frequencies
从图7可以看出:弯曲振动频率随波形钢腹板厚度的增加而增大,但前两阶弯曲振动频率的变化较小;随着频率阶数的升高,弯曲振动频率增幅更加显著。
3.4 剪力滞效应对弯曲振动频率的影响
为研究剪力滞效应对新型波形钢腹板组合箱梁桥弯曲振动频率的影响,将考虑剪力滞和不考虑剪力滞效应计算的前5阶弯曲振动频率进行比较,结果如表3所示。
表3 剪力滞效应对弯曲振动频率的影响
Tab. 3 Effect of shear lag on bending vibration frequencies
频率阶数 频率/Hz 误差/%考虑剪力滞 不考虑剪力滞1 3.692 3.724 0.87 2 12.807 13.183 2.94 3 24.261 25.423 4.79 4 36.398 38.591 6.03 5 48.657 51.930 6.73
从表3可以看出,剪力滞效应对新型波形钢腹板组合箱梁桥弯曲振动频率的影响较小,前5阶误差最大为6.73%,且前3阶增幅相对较大,第4阶频率及以后增长趋于平缓。
3.5 剪切变形对弯曲振动频率的影响
为研究波形钢腹板的剪切变形对新型波形钢腹板组合箱梁桥弯曲振动频率的影响,将考虑剪切变形和不考虑剪切变形计算的前5阶弯曲振动频率进行比较,结果如表4所示。
表4 剪切变形对弯曲振动频率的影响
Tab. 4 Effect of shear deformation on bending vibration frequencies
频率阶数 频率/Hz 误差/%考虑剪切变形 不考虑剪切变形1 3.692 3.865 4.49 2 12.807 14.935 16.62 3 24.261 31.707 30.69 4 36.398 52.000 42.86 5 48.657 73.558 51.18
从表4可以看出,波形钢腹板的剪切变形对新型波形钢腹板组合箱梁桥弯曲振动频率的影响较大,前5阶误差最大已高达51.18%,且随着频率阶数的升高不断增大。由此可知,此类桥型在计算弯曲振动频率时,剪切变形不可忽略。
3.6 不同理论所得基频的对比
为分析不同理论对求解新型波形钢腹板组合箱梁桥基频的适用性,根据Wood、Billing、Cantieni、Tilly和Jung等所提出的基频计算公式对新型波形钢腹板组合箱梁桥的基频进行了分析。将不同理论计算的基频与文献[19]的基频值、本文基频值及《公路桥涵设计通用规范》(JTG D60—2015)求解的基频值进行比较,结果如图8所示。

图8 不同理论方法所得基频对比Fig. 8 Comparison of fundamental frequencies obtained by different theoretical methods
从图8可以看出,随着跨度的增大,基频值不断减小。当跨度小于30 m时,不同理论方法所求得的基频值差异较为明显,且跨度越小,结果相差越大;当跨度大于30 m且小于40 m时,以上8种方法所求得的基频值相差较小。
4 结 论
1)本文考虑剪切剪滞双重效应的影响,推导了新型波形钢腹板组合箱梁桥弯曲振动频率的计算公式,并用实测结果和ANSYS有限元结果对计算公式的正确性进行了验证。
2)弯曲振动频率随高跨比的增大而增大。当高跨比小于0.05时,弯曲振动频率的增幅较为平缓;当高跨比大于0.05时,弯曲振动频率的增幅较为显著。弯曲振动频率随宽跨比的增大而略有增大,但整体增幅不明显。
3)弯曲振动频率随波形钢腹板厚度的增加而不断增大,但前两阶弯曲振动频率所受影响较小;随着频率阶数的升高,弯曲振动频率增幅更加显著。
4)剪力滞效应对新型波形钢腹板组合箱梁桥弯曲振动频率的影响较小,前5阶频率最大误差为6.73%;波形钢腹板的剪切变形对弯曲振动频率的影响较大,前5阶频率最大误差为51.18%,且随着频率阶数的升高不断增大。
5)本文方法所求新型波形钢腹板组合箱梁桥的基频与实测值、Cantieni理论公式值吻合良好。当简支梁跨度在30 m内时,不同理论方法所求得的基频值差异较为明显,且跨度越小基频相差越大;当跨度在30~40 m范围内时,不同理论方法所求得的基频值相差较小。

