融合延迟变换和张量分解的金融时序预测算法

李大舟，于锦涛，高 巍，陈思思，朱风兰

(沈阳化工大学 计算机科学与技术学院，辽宁 沈阳 110142)

0 引 言

金融时间序列预测对于社会有很大的价值，有助于把握社会经济、市场经济走向。对于经济领域，金融时间序列预测更是一项非常重要的预测工具。

自回归移动平均模型[1](autoregressive integrated moving average model，ARIMA)具有很强的灵活性，是如今应用广泛的模型之一。然而，在预测分析中使用ARIMA模型会导致预测值的偏差。季节时间序列模型(seasonal differential autoregressive sliding average model，SARIMA)[2]是在原有模型的上加上时间序列的季度变化特性，从而形成的短期预测模型，该模型会在一定程度上提高线性建模能力。本文在对原始时序数据进行处理时，单一地使用ARIMA模型会引起预测的偏差，因此本文选用SARIMA模型。然而，大多数现有的SARIMA模型需要一个接一个地预测多个时间序列。SARIMA模型没有考虑相关时间序列之间的内在关系，这将导致这些性能可能会受到限制。因此就需要张量分解来更好地捕捉内在的时间相关性。

张量分解是从张量数据中提取有价值信息的一种强大的计算技术[3]。利用这一优势，基于张量分解的方法可以同时处理多个时间序列，并获得良好的预测性能[4]。例如，提出了与AR模型集成的Tucker分解[5]。获得高阶时间序列预测的多线性正交AR(MOAR)模型和多线性约束AR模型。此外，一些工作将分解与神经网络结合起来，用于更复杂的张量时间序列[6]。

多路延迟嵌入变换[7]是一种新兴的技术，它将可用数据转换为高阶块Hankel张量。本文沿着时间方向对多个时间序列进行多路延迟嵌入变换，从而得到一个高阶块Hankel张量，它表示每个时间点的所有时间序列作为高维嵌入空间中的张量。

本文利用块Hankel张量，利用低秩Tucker分解，利用正交因子矩阵投影到核心张量。这些投影矩阵被共同用于最大限度地保持核心张量之间的时间连续性，这种方法可以比原始时间序列数据更好地捕捉内在的时间相关性。同时，本文将经典SARIMA模型张量化，并将SARIMA模型直接应用于核心张量上。最后，本文在下一个时间点预测一个新的核心张量，然后通过逆Tucker分解和逆多路延迟嵌入变换同时获得所有时间序列数据的预测结果。本文通过低秩Tucker分解将块Hankel张量与SARIMA模型结合成一个新的预测模型。该模型利用嵌入空间中的低秩数据结构，捕捉多个时间序列之间的内在相关性，从而获得良好的预测结果。

1 构建多路延迟变换和张量分解的SARIMA算法(BHT-SARIMA)

文中具体变量定义见表1。

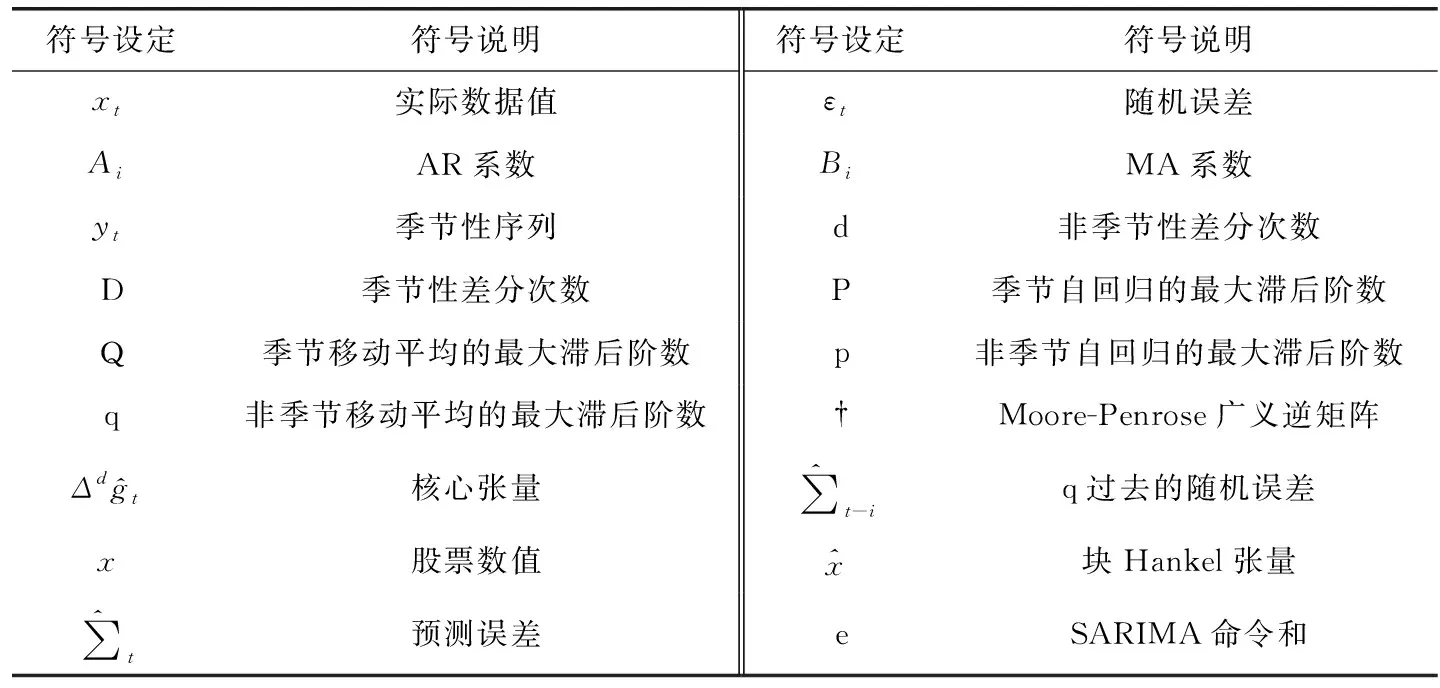
表1 变量定义

本文为了有效和高效地解决时间序列预测问题，通过低秩塔克分解将块汉克尔张量与SARIMA模型结合起来。该方法的主要思想如图1所示。首先，本文采用多路延迟嵌入变换将时间序列表示为低秩块汉克尔张量。然后本文在连续核心张量上显式地使用季节性差分自回归滑动平均模型来预测未来的样本。然后，本文利用塔克分解将高阶张量投影到压缩核心张量中，进而得到预测结果。

图1 本文提出的算法构建过程

1.1 多路延迟嵌入变换张力化Hankel张量

张量的维数是有序的，每个维数都是它的一种模式。张量是多维数据的专有名词。向量和矩阵可分别被认为是一阶和二阶张量。在现实世界中，很多数据比如视频等都是以张量形式存在。张量分解是一种强大的计算技术，通过将原数据分解从中提取有价值的特征，其中从低阶张量扩展到高阶张量是很重要的。用一组三阶张量表示从低阶张量扩展到高阶张量是很简单的，整体变化如图2所示。

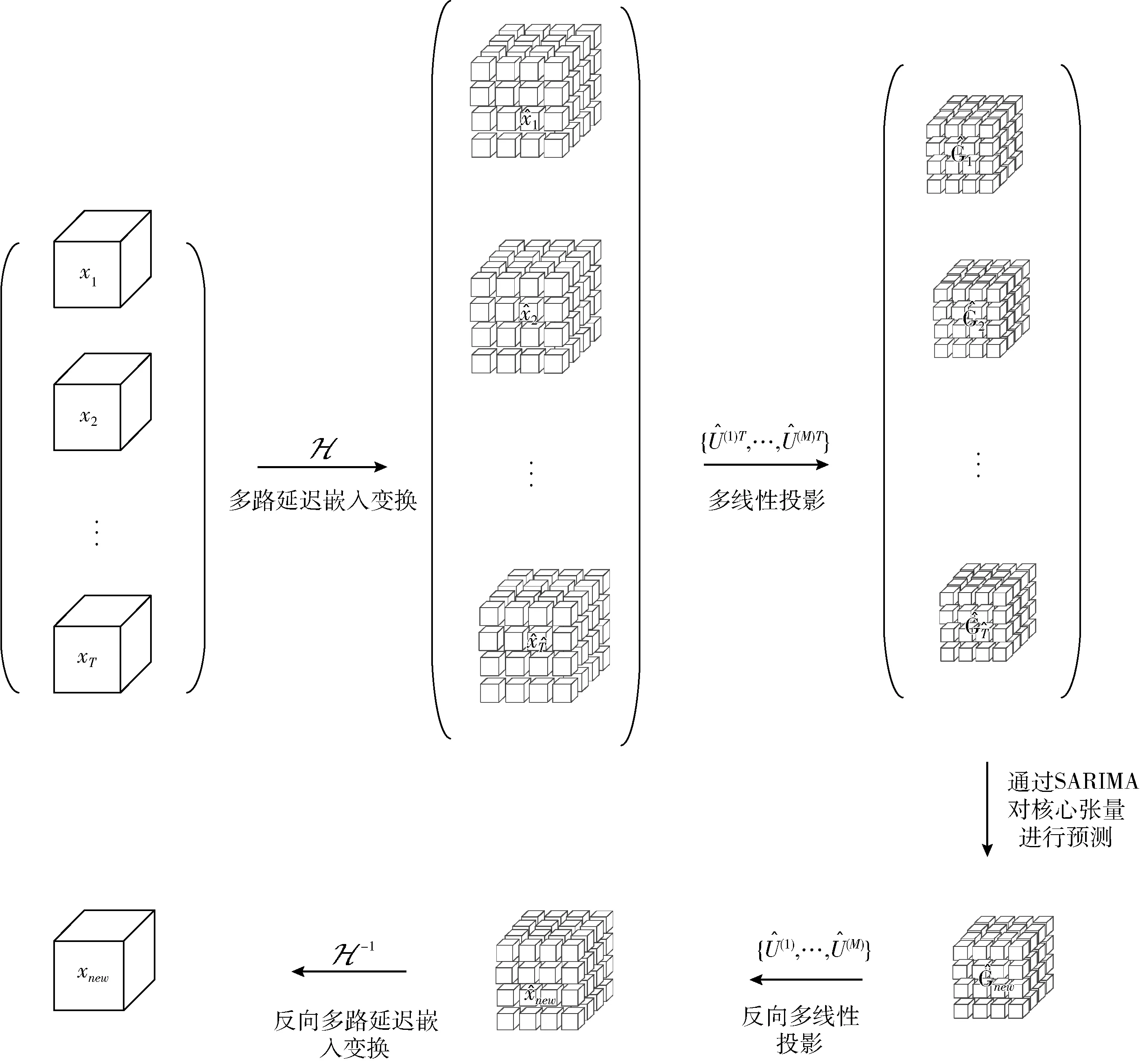
图2 三阶张量扩展到高阶向量过程

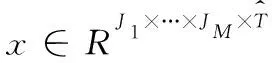
(1)

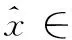
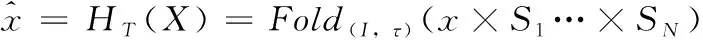
(2)

当SN∈τN(IN-τN+1)×IN是一个重复矩阵，并且Fold(I,τ)τ1(I1-τ1+1)×…×τN(IN-τN+1)→τ1(I1-τ1+1)×…×τN(IN-τN+1)中输入张量构造高阶块Hankel张量。从而，本文得到了的逆多路延迟嵌入变换

(3)

其中，†是Moore-Penrose逆矩阵。Moore-Penrose逆矩阵是对广义逆矩阵的进一步约束，它能保证解的唯一性。图3中展示了股票数据转换过程的实例。

图3 表示原始数据的逆多路延迟嵌入变换

通过这种方法，本文得到了高维嵌入空间中的块Hankel张量，其中每个块Hankel张量包含所有时间序列在同一个时间点的股票数据。本文只沿着时间模式应用多路延迟嵌入变换，因为多个时间序列之间的关系通常不比它们的时间相关性强。因此，没有必要对所有可能没有意义的模式进行多路延迟嵌入变换，同时花费更多的时间。

1.2 Tucker分解

本文应用正交Tucker分解来探索在低秩嵌入空间中作为压缩核心张量的多个时间序列之间的内在相关性。通过低秩Tucker分解将块Hankel张量与SARIMA模型合并，可以有效地解决多重时间序列预测问题。对于一个三阶张量，由Tucker分解可以得到3个二阶的因子矩阵和一个三阶的核张量。换句话说：Tucker分解通过因子矩阵(也称作映射矩阵)将原张量映射到一个具有良好特性的核张量。一个向量由粗体小写字母x∈I。 矩阵用粗体大写字母X表示X∈I1×I2。 高阶(N≥3)张量由粗体书法字母表示I1×I2…IN， Tucker分解具有明确的物理意义，它是高阶PCA的一种形式，它可以体现原始张量的大部分性质，因此本文的分解形式采用Tucker分解。

1.3 张量化SARIMA模型

首先设xt作为任意时间点的实际数据值。xt可以看作是过去p值和过去q观测随机误差的线性函数，即ARIMA(p，q)模型

(4)

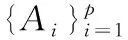
(5)

设季节性序列为yt， 则一次周期为s的季节差分表示为

Δsyt=(1-Ls)yt=yt-yt-s

(6)

通过使用D季节差异使非平稳季节序列来过渡道平稳序列，并且在此基础上建立季节时间序列预测模型

(7)

假设μt序列具有平稳性、非自相关性。当μt具有非平稳性且存在ARMA因子时，则把μt描述为

∅p(L)Δdμt=θq(L)νt

(8)

将上述公式结合在一起，可得到

(9)

其中，P、Q、p、q、d、D定义如表1所示。上式称为 (p,d,q)(P,D,Q)s阶季节时间序列模型。上述模型用SARIMA(p,d,q)(P,D,Q)s表示。对于季度序列，s=4；对于月度序列，s=12。

1.4 构建BHT-SARIMA算法模型

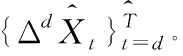
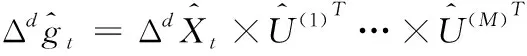
(10)

(11)

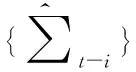
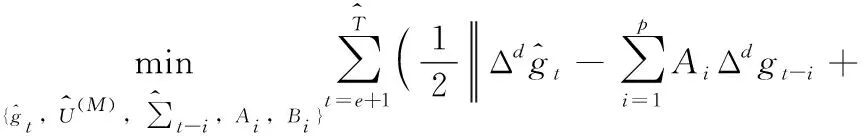
(12)

其中，e是SARIMA模型命令的和，也是每个时间序列的最小输入长度。接下来，本文使用增广拉格朗日方法来解决这个问题。为了便于式(12)的推导，通过沿着模型展开每个张量变量，重新表示优化问题

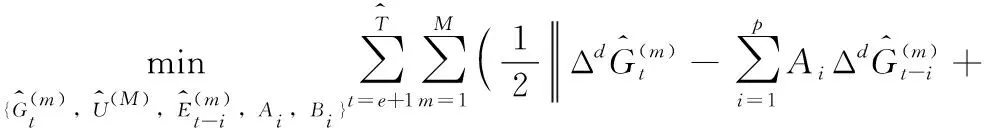
(13)

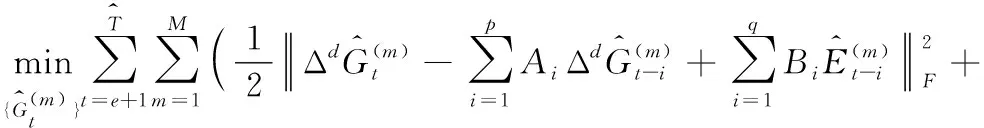
(14)

(15)

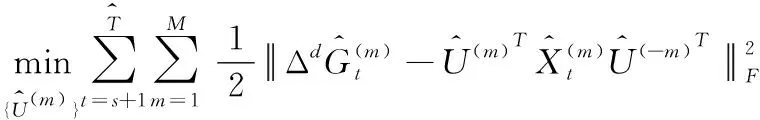
(16)

(17)

本文通过沿最后一种模式消除的正交约束来展现出全正交性的效果(视为嵌入空间中每一个时间模式)。这种方法可能会放松对时间平滑性的严重约束，从而使所提出的模型对参数的可变性更加灵活和稳健，从本文的实验结果中可以观察到。本文在没有正交约束的情况下放宽了最后的时间模式，然后计算了方程的偏导。因此，本文更新它为

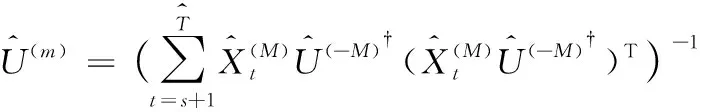
(18)

(19)

计算这个函数的偏导，使其等于零，可得到

(20)

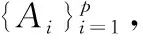
1.5 预测XT+1

(21)

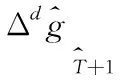
综上所述，本文提出的融合多路延迟变换和张量分解的SARIMA算法(BHT-SARIMA)伪代码如下：

Algorithm:BHT-SARIMA算法

(1)输入：股票时间序列数据:x∈I1×I2…IN， (p,d,q),(P,D,Q),k,tol

(2)步骤1 多路延迟嵌入变换张力化Hankel张量

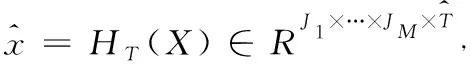
(5)步骤2 利用Tucker分解来检测SARIMA

(8)fork=1,…,K

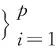
(11)forn=1,…,M

(15)fori=1,…,q

(18)步骤3 预测XT+1

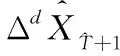
2 实验设计

2.1 金融时序预测的实验环境和实验数据集

本实验在macOS10.15系统下进行，使用Intel@i7-8850H作为计算单元，内存为32 GB，编程语言为python，本文具体实验配置见表2。

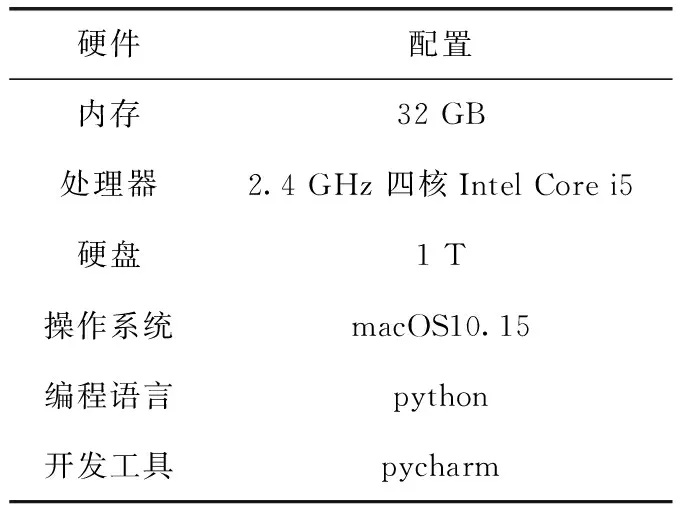
表2 实验环境配置

本文以上海证券综合指数、上海证劵综合指数50、中证指数、ST中华A股指数为研究对象。财务时序数据样本采用4支股票指数数据，2010年1月1日至2020年4月15日，4支股票共计9996个交易日的股票历史数据。本文选取调整后的收盘价作为本模型的预测目标，如图4所示。

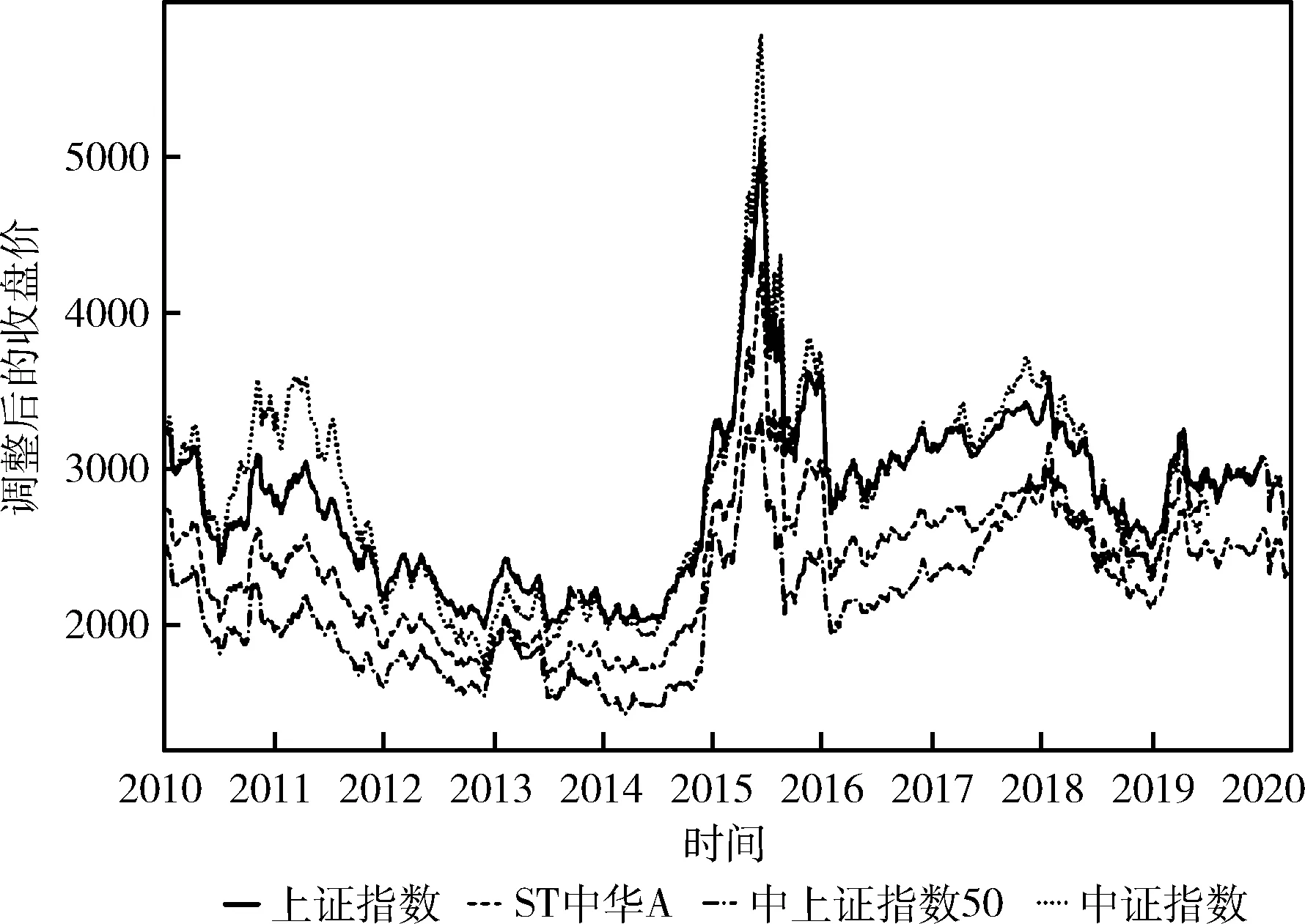
图4 4支股票数据变化

2.2 参数设置

本文根据2010年～2020年上证指数数据,在这里按每一月的变化数据作为实验案例。构建季节时间序列模型需要原始时序数据具有平稳的特性，如果原有时序数据为非平稳的数据，则需要对其进行一阶差分运算，进而得到平稳的时序数据，最后根据平稳的时序数据来进行建模。由图4可以看出股票数据波动较大，进而对其做一阶差分，得到图5，因为SARIMA模型需要的数据的平稳性，在此设定波动值的范围为(-400，200)则为稳定，因此得到一阶差分后数据波动相对平稳，则不再进行二阶差分，所得到的一阶差分图如图5所示。

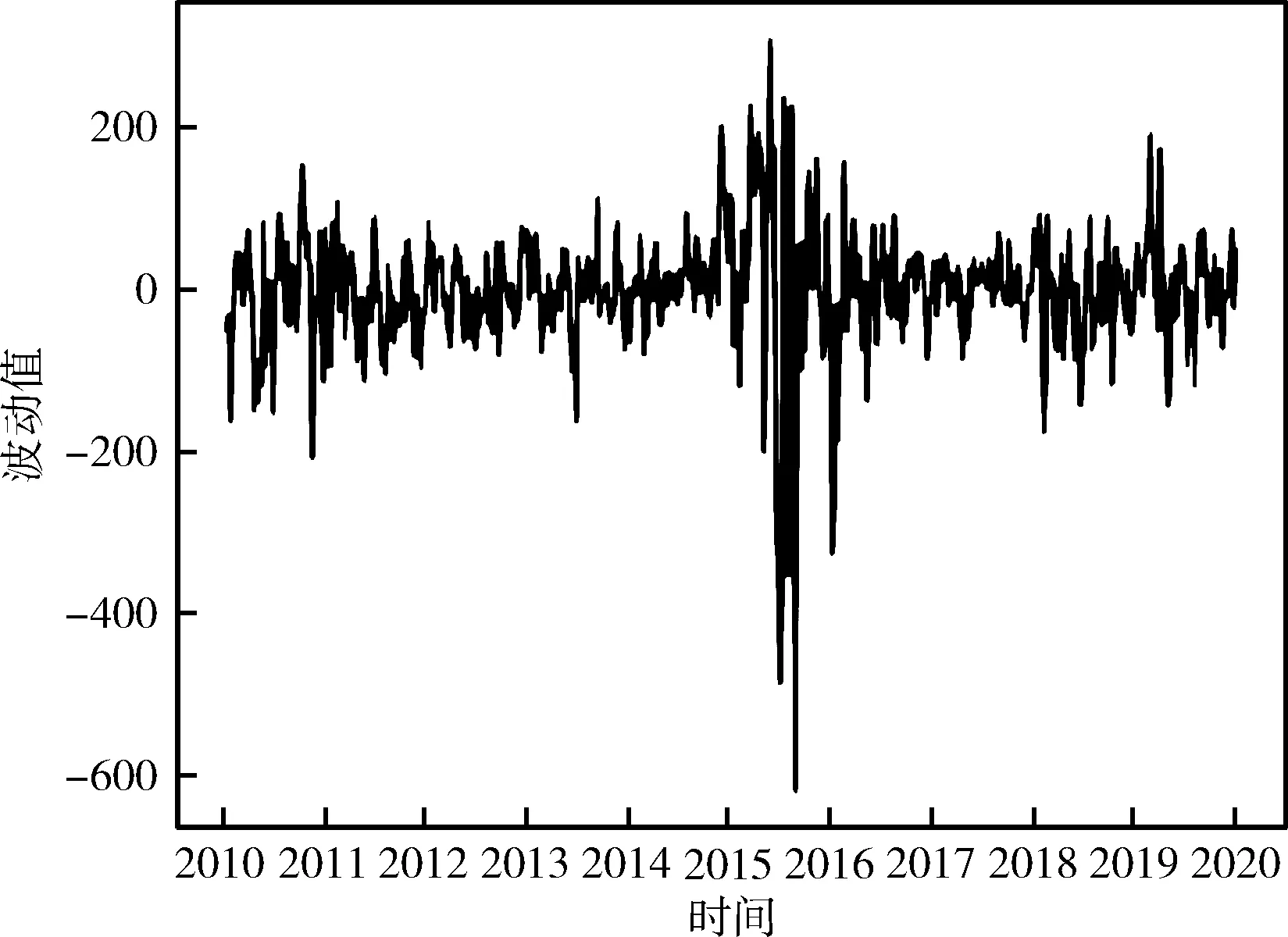
图5 股价数据一阶差分变化

由于原始时序数据具有不平稳的特性，因此本文对其进行一阶逐期差分和一阶季节差分操作，进而得到平稳性的时序数据。因此d，D取1。此外，从自相关和偏自相关分析图来看，自相关系数在随机区间范围内，自相关函数拖尾，因此q=3或4，Q=1为宜。由于偏自相关系数在随机区间范围内，偏自相关函数拖尾，因此最好是p=2或3，P=1。因为是按月划分，则s=12。所得到的自相关分析(ACF)和偏自相关分析(PACF)如图6、图7所示。

图6 自相关分析(ACF)

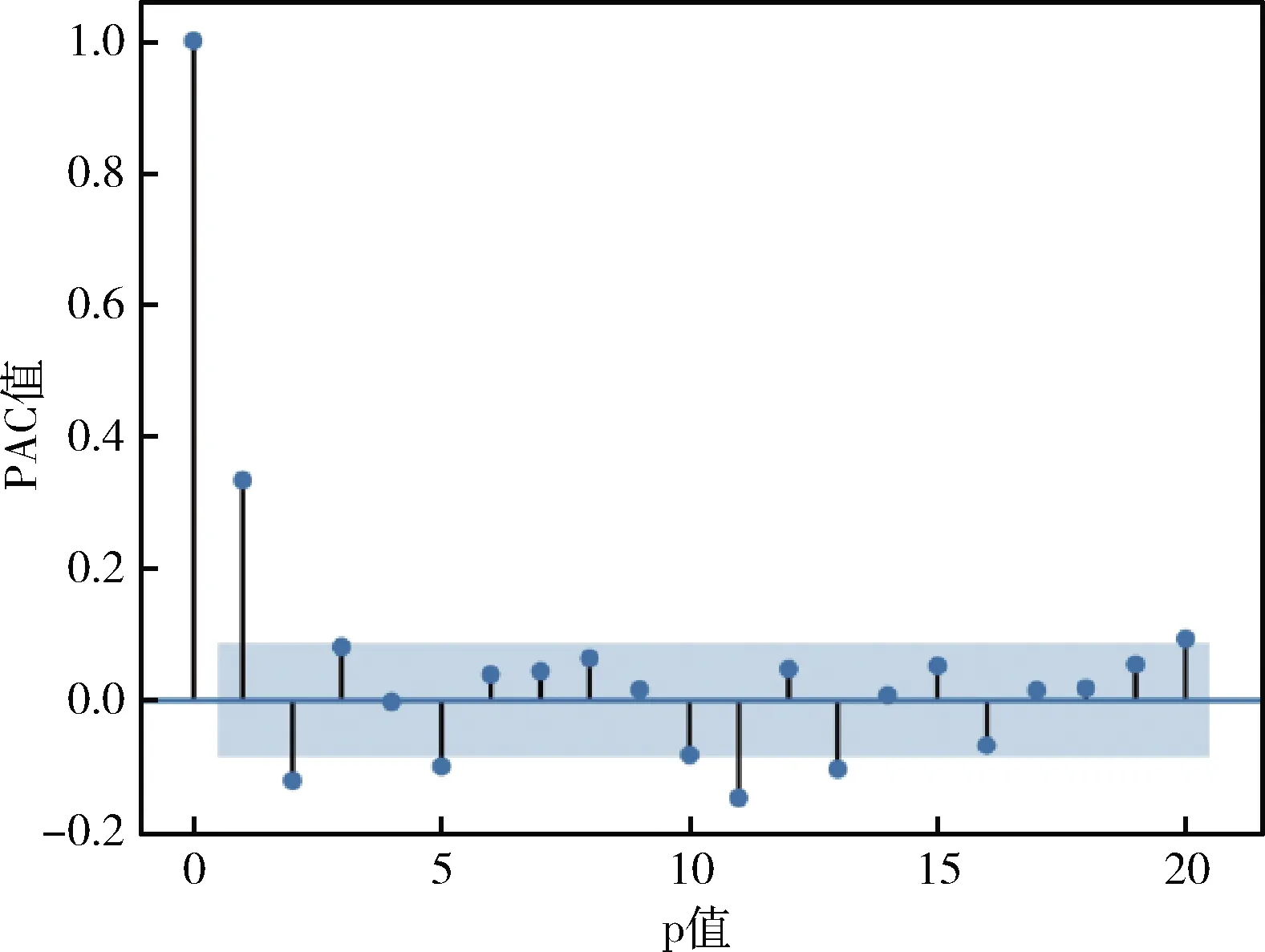
图7 偏自相关分析(PACF)

因此，本文得到的模型如下SARIMA(2，1，3)(1，1，1)12， SARIMA(3，1，3)(1，1，1)12， SARIMA(2，1，4)(1，1，1)12， SARIMA(3，1，4)(1，1，1)12这4种指标模型。

2.2.1 SARIMA模型的评价指标

本文实验结果采用R2、 赤池信息量准则(Akaike information criterion，AIC)、施瓦茨准则(Schwarz criterion，SC)3种评价指标对SARIMA模型进行筛选。

R2表示回归方程在多大程度上解释了因变量的变化，也是可以表现出方程对观测值的拟合程度如何。R2值越大，

则模型拟合程度越好

(22)

AIC准则是评定最优配置的指标，它是通过拟合精度和未知参数得到加权函数来评定的。AIC函数值越小，模型则越优

(23)

SC准则是比较所含解释变量个数不同的多元回归模型的拟合优度。SC函数值越小，模型则越优

(24)

2.2.2 SARIMA模型设定

根据各个模型精度指标结果，发现模型SARIMA(2，1，3)(1，1，1)12的AIC和SC值为4种模型中较小，R2值4种模型中较大，因此可考虑采用SARIMA(2，1，3)(1，1，1)12进行建模，对比结果见表3。

2.3 金融时序预测的评价指标

本文实验结果采用归一化均方根误差(normalized root mean square error，NRMSE)对预测性能进行评价。NRMSE是时间序列预测性能的常用指标，用来衡量观测值和目标值之间的偏差，NRMSE就是将RMSE的值变成(0,1)之间，NRMSE 始终是非负的，NRMSE值越小，说明预测性能越准确。NRMSE评价指标的公式为

(25)

表3 4种模型的精确指标

2.4 实验结果分析

本文比较了9种竞争方法：①经典ARIMA、Vector AR(VAR)和XGBoost；②两种流行的行业预测方法：Prophet和DeepAR基于神经网络的方法；③TTRNN和门控循环单元(GRU)；④基于矩阵/张量的两种方法：TRMF和MOAR；此外，本文将得到的块Hankel张量作为MOAR的输入，将评价多路延迟嵌入变换与MOAR结合得到BHT-MOAR模型，以评价多路延迟嵌入变换与张量分解的有效性，得到的结果如图8所示。

结果如图8所示：在所有情况下，BHT-SARIMA模型都优于所有现有的竞争算法。特别是对于较短的时间序列，BHT-SARIMA模型显示出了更大的优势。GRU模型和SARIMA模型得到了第二的好结果。注意BHT+MOAR模型在所有情况下的性能都比MOAR模型好。验证了结合张量分解应用多路延迟嵌入变换的有效性。

图8 各个模型NRMSE值比较

在图9中展示了预测的平均时间成本。虽然在某些情况下TRMF模型略慢于VAR模型，但由于其核心部分是用C编程实现的，所以总体上是最快的算法。BHT-SARIM模型A是第二快的方法，但本文的实现并没有针对效率进行优化，因为本文强调的是准确性。MOAR模型比本文提出的算法的慢，主要是因为它不直接使用低维核心张量进行训练。在某些情况下，ARIMA模型和GRU模型是性能第二好的算法，但它们是最慢的方法(平均比BHT-SARIMA模型慢500倍以上)。

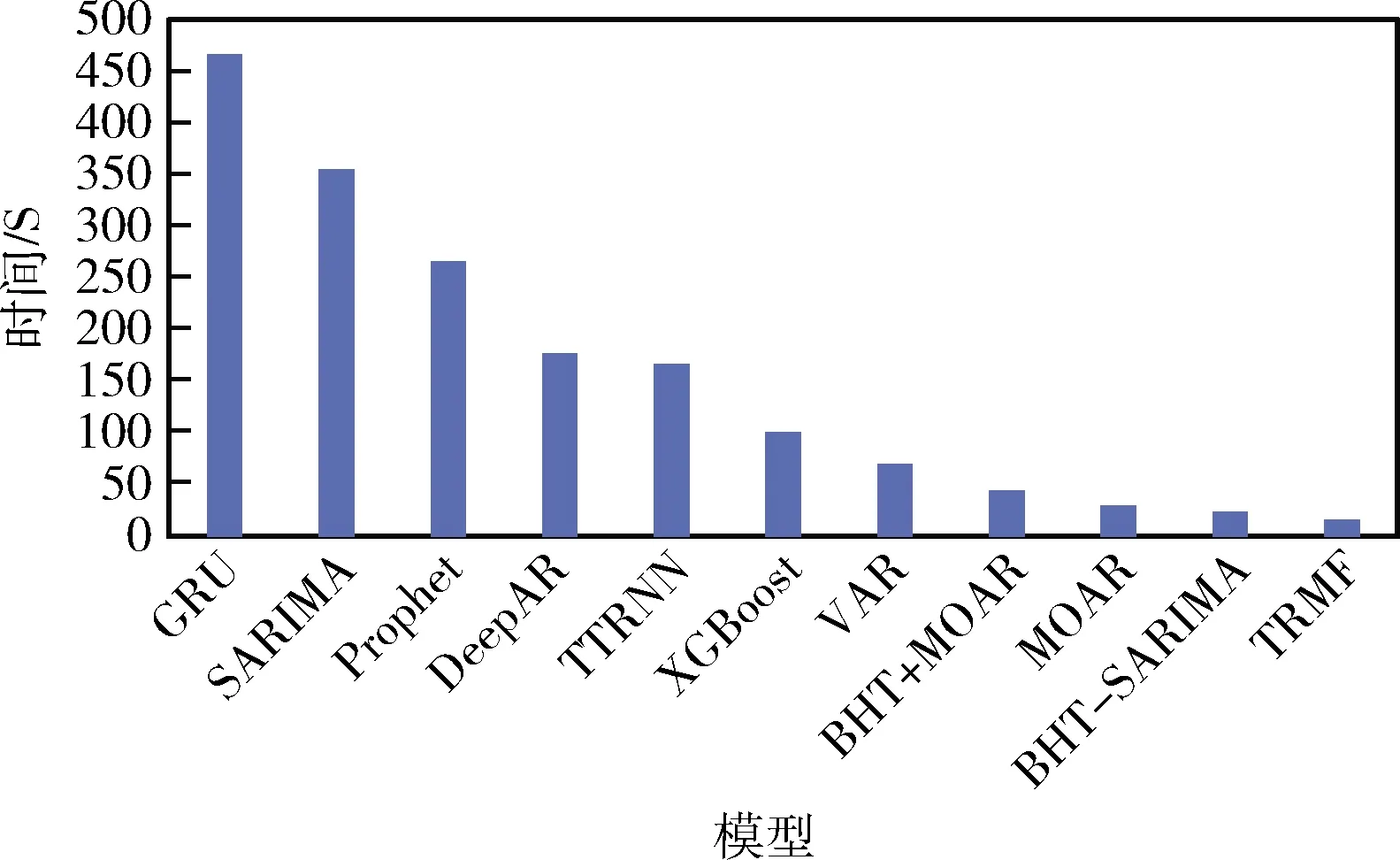
图9 各个模型计算时间比较

最后，随着迭代次数的增加，准确率最后可以达到约为0.810 067 99。其中本文挑选了3个算法模型与本文BHT-SARIMA算法模型进行比较，3个算法模型为：XGBoost、SARIMA、VAR，准确率比较如图10所示。

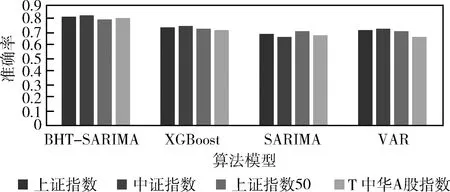
图10 表示各算法模型准确率的比较

3 结束语

当今，股市估值在整个经济中占据着首要的地位，如果可以提出准确的金融时序预测结果对于规避股市风险和股市交易操作具有直接的指导作用。在本文中提出了将一种新的模型和金融相结合，形成一种新的金融时序预测算法。该方法利用多路延迟嵌入变换对SARIMA模型张量化并进行Tucker分解。这种模型有效解决了多条时间序列会产生的平稳性问题，从而提高预测的准确率。本次实验采用上海证券综合指数、上海证劵综合指数50、中证指数、ST中华A股指数作为基本数据集，实验对比分析了现有的各种预测模型方法以及各种模型计算的时间成本，多路延迟变换和张量分解的SARIMA算法得到的预测效果有了很大的提升，计算时间成本也得到了很好的减少。