三维模型任意剖面的程序式凹凸映射生成算法
李 冰,贾世宇
(青岛大学 计算机科学技术学院,山东 青岛 266071)
0 引 言
三维模型在医学、虚拟现实、网络游戏等领域[1-3]应用广泛。为提高屏幕空间中三维模型的真实感,通常需要对模型进行真实感图形渲染。目前常用的渲染方法有纹理映射和凹凸映射。纹理映射[4,5]可以实现物体表面的颜色纹理,但不能体现物体表面凹凸不平而形成的粗糙质感。与纹理映射相比,凹凸映射[6]不需要增加对象的几何复杂度,就可以生成表面复杂的视觉效果,且凹凸映射可以对物体细节特性进行展示,使其更接近自身真实的模样,更能增加绘制对象的真实程度。
在三维模型发生切割操作时[7,8],如虚拟手术[9,10]中,切割面可以直观展示模型内部纹理结构和特征。三维模型切割面上的纹理可以使用三维纹理[11]实现,三维纹理可以存储模型内部任意点的颜色信息,但并不能存储法线信息。此外,三维纹理本身存在获取困难和占用存储空间大的问题。虽然使用较广的二维凹凸映射将表面的法线扰动信息存储在二维纹理中,但由于模型内部任意点的法线无法从表面的法线计算出来,因此并不适用于任意三维剖面。
为解决上述问题,本文提出一种剖面上的程序式凹凸映射生成算法。该算法结合模型内部微观结构将剖面分为3类,并对每类剖面分别应用程序式凹凸映射算法,从而在任意剖面上生成有内部结构的凹凸映射纹理。与三维纹理方法相比,该算法结合模型内部不规则的微观结构,能有效提高剖面的真实感。同时,通过程序式凹凸映射实现方法,可以在程序中直接生成扰动后的法线,而不需要将凹凸图中的高度信息转换成法线扰动信息,能有效模拟更真实的视觉效果。且算法使用着色语言shader编程实现,可以有效提升程序运行速度。
1 相关工作
Blinn等[12]首先提出了凹凸映射的方法,他们通过一个扰动函数对物体表面的法线进行扰动,实现在光滑物体表面附上粗糙纹理的功能。还可以利用扰动函数改变物体表面的参数,在模拟头发、衣服等物体方面取也得较好效果。任等[13]提出一种改进的凹凸映射技术-视差映射,该方法根据存储在纹理中的几何信息对采样点的纹理坐标进行扰动,可以产生更为真实的层次感,且具有计算量小等优点。Yao等[14]提出一种基于凹凸映射的海平面场景仿真方法,该方法使用凹凸映射技术模拟不同频率的波浪,解决了海平面模拟过程中的实时性与真实感相矛盾的问题。Anouar等[15]通过将旋转映射与凹凸映射相结合来提高三维旋转模型的真实感,产生较为逼真的三维模型褶皱效果。
在噪声研究方面,Perlin等[16]提出一种自然噪声生成算法,称之为经典柏林噪声。目前,柏林噪声已被广泛应用于虚拟游戏、计算机仿真等领域。Conde等[17]基于柏林噪声,提出了一种定义非均质固体微观结构的方法,该方法能够准确地表示原始材料的比例、大小和形状。王等[18]通过二维柏林噪声控制花瓣和叶片的卷曲程度,实现花卉器官的三维重建。陈等[19]以柏林噪声为基础,提出一类可以用于细化心脏纹理图的新方法,可对心脏客观结构进行较好的模拟。
程序式纹理[20]是用数学公式描述物体表面的纹路,通过算法在程序中直接生成图形的纹理。Liu等[21]提出一种基于实例生成新过程纹理的框架,其中,新的纹理可以具有与输入示例相同的感知属性。Wang等[22]提出一种基于样本的实体纹理合成算法,该算法将二维纹理贴片技术扩展到三维肝动脉实体,来模拟三维空间中各向异性的实体纹理。
2 程序式凹凸映射算法
为提高模型剖面视觉效果,本文提出一种针对剖面的程序式凹凸映射生成算法。该算法首先使用球、圆柱等作为模型内部的微观颗粒对剖面的微观结构进行建模,然后将剖面分为撕裂面、空心切割面、实心切割面3类。最后对每类剖面均应用程序式凹凸映射算法得到剖面渲染结果。
2.1 微观结构建模
为模拟任意剖面上的凹凸映射效果,在微观结构建模过程中,本文假定模型内部由许多微观颗粒构成,选用球、圆柱等作为模型内部的微观颗粒,并使用经典Perlin噪声生成三维噪声纹理加以扰动(噪声纹理大小为:256×256×256),使其更加接近真实情况。
在初始条件下,微观颗粒排列成规整的三维网格,并且具有相同的大小和间距。然后对每个颗粒,使用其在三维网格中的整数坐标到三维噪声纹理中进行采样,并使用采样值对颗粒的大小和位置进行扰动,产生不规则的结构。其中,噪声纹理的每个纹素存储R,G,B,A这4个分量,R,G,B,A是通过噪声计算得到的返回值。对于球使用R,G,B分量扰动球心位置,使用A分量扰动半径;对于圆柱使用R,G,B分量用于扰动圆柱底面圆心位置,使用A分量扰动底面圆的半径和圆柱的高度。在整个过程中,为避免颗粒偏离规整网格格点过远,对于半径的扰动均未超过相邻颗粒之间间距的一半。
2.2 球形颗粒剖面算法
2.2.1 球形颗粒撕裂面
在剖面是撕裂面的情况下,内部的球形颗粒会偏向包含其球心的一侧,另一侧的相对位置将产生一个空腔,但球形颗粒自身结构并没有被破坏。
假定目标点为P(x,y,z), 目标点处剖面的单位法线向量为Ns。首先计算与P点最近的三维网格整数坐标PI,然后使用2.1中的算法获取PI及其相邻的共27个整数坐标对应颗粒的球心和半径,并针对这些球体,分别使用式(1)计算P到该球球心O的距离dist,当dist≤R时,说明P在该球之内。否则,说明P不在任何球之内,则P处的法线向量就是Ns,没有扰动
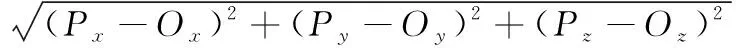
(1)
如图1所示,当P在某个球心为O,半径为R的球体之内时,则需要根据球心与剖面的位置情况进一步计算扰动的法线。位置情况可以通过计算点积正负判断,如下式所示:其中,当h≤0,说明球心在剖面内侧,否则在外侧
h=Ns·(O-P)
(2)

图1 球形颗粒撕裂面扰动法线计算方法
当球心在剖面内侧时,说明球体嵌在剖面内侧,如图1(a)所示。在这种情况下,从P点沿T=Ns方向发出一条射线,计算该射线与球面的交点Q。然后取Q点处的球面外指法线作为扰动的法线Np。公式为
Np=(Q-O)/|Q-O|
(3)
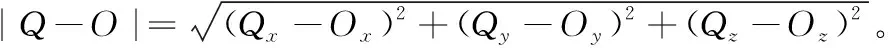
当球心在剖面外侧时,即球体嵌在对向的剖面中,则本地剖面内侧会形成一个空腔,如图1(b)所示。在这种情况下,从P点沿T=-Ns方向发出一条射线,计算该射线与球面的交点Q。然后取Q点处的球面内指法线作为扰动法线Np。计算公式为
Np=(O-Q)/|O-Q|
(4)
其中,交点Q可以表示为:Q=P+uT,u为参数坐标且u≥0。且Q满足方程: (Q-O)·(Q-O)=R2, 将Q点坐标代入方程中,可得如下关于u的二次方程
au2+bu+c=0
(5)
其中
(6)
解方程(5),可得u的值为
(7)
取非负根作为u的值,即可得到Q点坐标。
2.2.2 球形颗粒空心切割面
在剖面是切割面的情况下,与剖面相交的内部颗粒则被切为两半。本文假定内部颗粒有两种情况:一种内部为液体,切开后液体流失形成空腔,将这种情况称为空心切割;另一种内部为固体,切开后形成实心碎片,将这种情况称为实心切割。
对空心切割面的情况,其法线计算方法与撕裂面情况相似,区别为空心切割面只需判断任意一点P是否落在球内而不需要判断球心与剖面的位置关系,当P落在某个球体之内时均使用图1(b)所示的方法计算扰动的法线。
2.2.3 球形颗粒实心切割面
在剖面为实心切割面情况下,与剖面相交的球均会在剖面上形成一个圆形截面,因此本文假定剖面上不在球体内部的点均向内缩进一段距离t,将球与剖面相交的圆形截面暴露在外,从而产生凹凸效果。为简化计算,本文将暴露在外的部分设为以圆形截面为顶面的圆台,且圆台的侧面倾角为45°。如图2所示,实心切割面扰动法线计算方法与前两种情况类似。
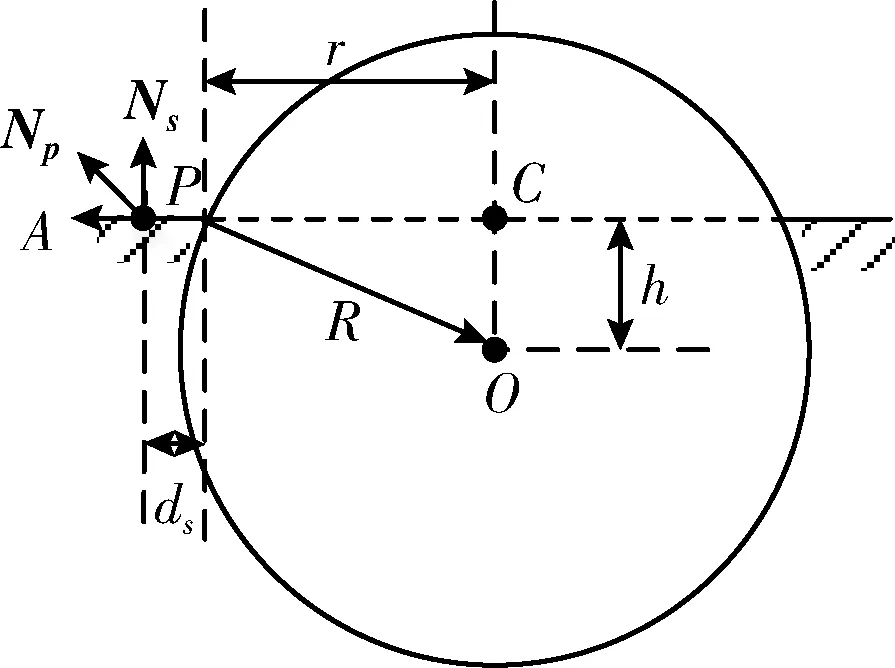
图2 球形颗粒实心切割面扰动法线计算方法
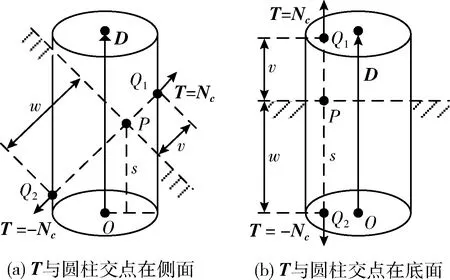
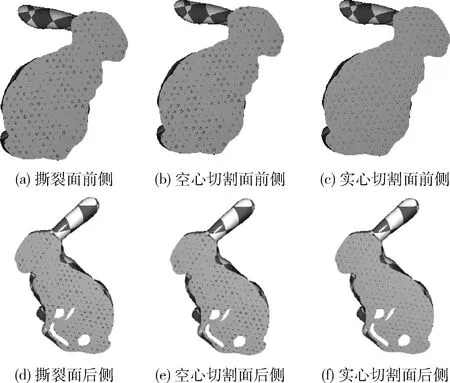
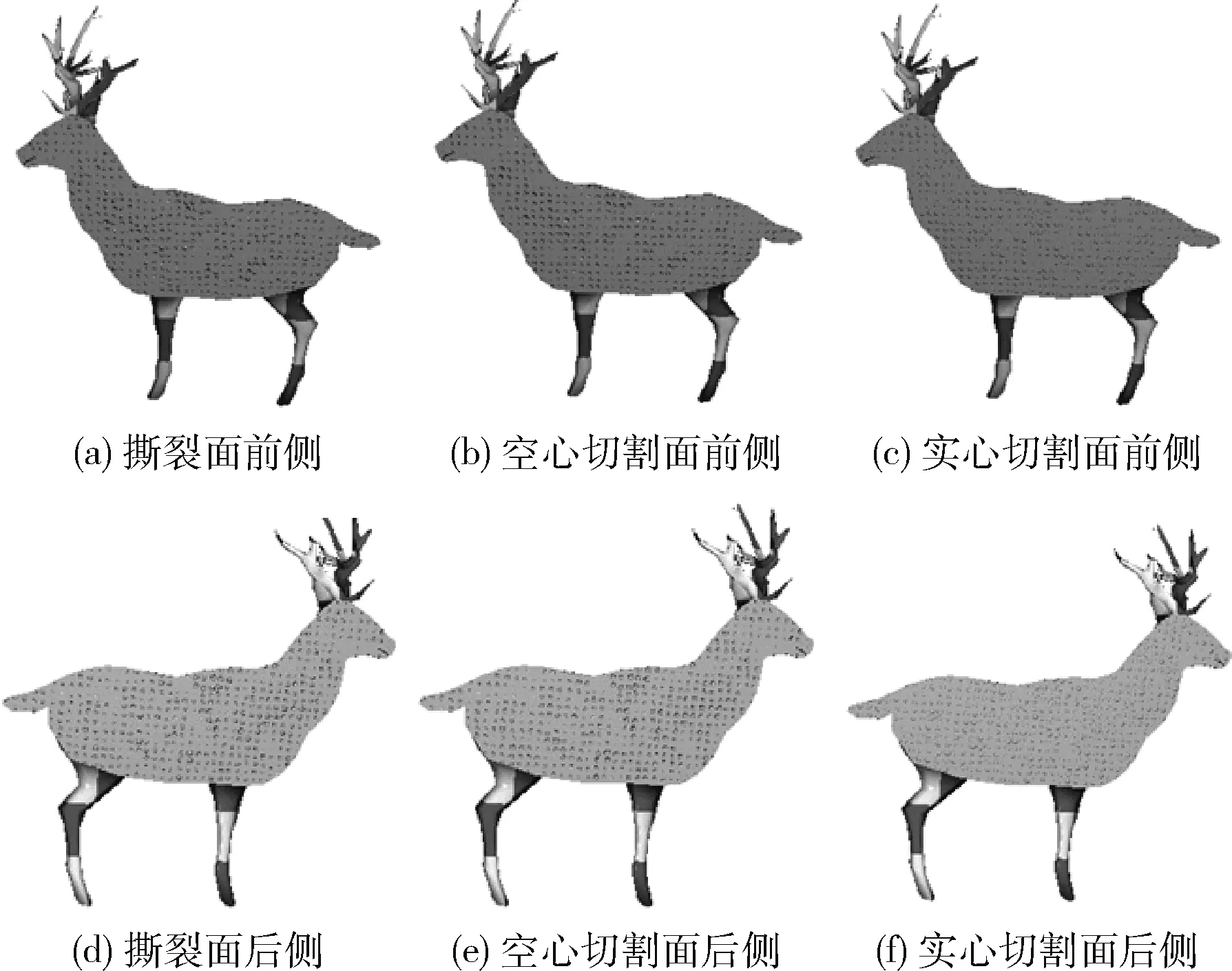
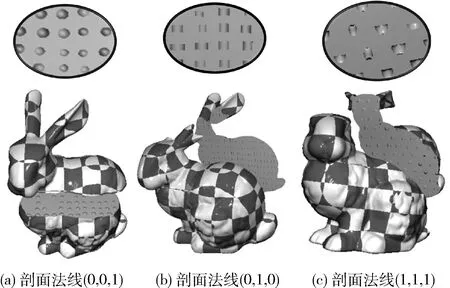
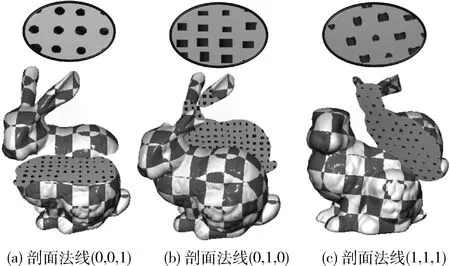
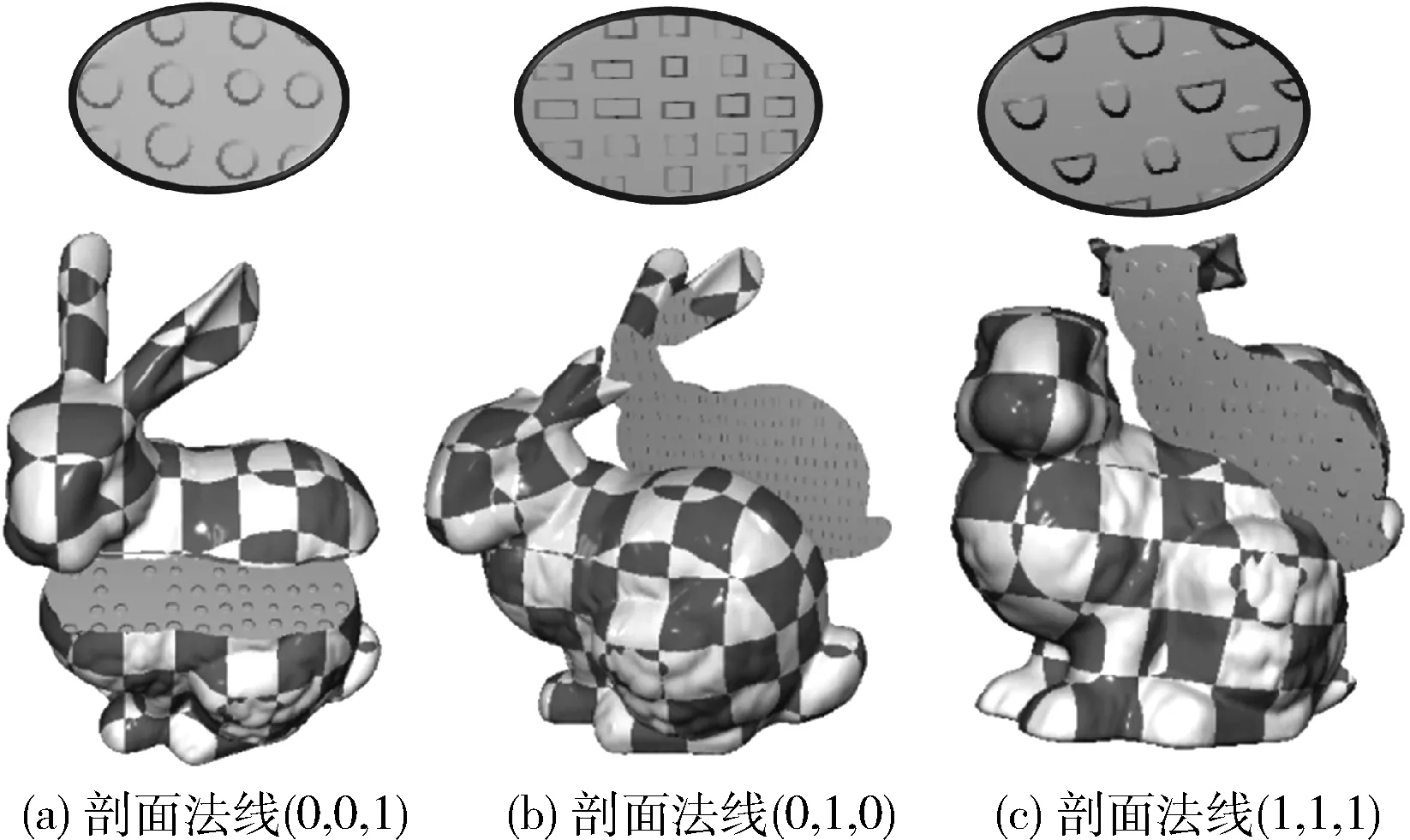
首先获取与P相邻的27个球体,并对每个球体进行遍历,判断P是否在其内部。若P在某球体内部时,结束球体遍历,若不在,使用式(2)计算h的值,当 |h| (8) 当球体遍历结束后,会存在以下3种情况: (1)P落在某个球体之内; (2)P不在任何球体之内,没有球体与剖面相交; (3)P不在任何球体之内,有球体与剖面相交。 对于(1)和(2),P处的法线向量为Ns,没有扰动;对于(3),取所有ds值中的最小值dmin,并根据dmin对扰动情况进行判断。当dmin>t(阈值t为球向内缩进的距离,取值为球间距值的0.07倍)时,则说明P处的法线向量仍然是Ns,没有扰动。否则说明P落在某个圆台的侧面上。从圆心指向P的单位向量A为 A=(P-Cmin)/|P-Cmin| (9) 其中,Cmin代表dmin对应的圆心,dmin对应的半径记为rmin。然后使用下式计算扰动的法线Np Np=(Ns+A)/|Ns+A| (10) 当球与任意平面相交时,剖面形状均为圆形;而当圆柱与剖面相交时,可能产生多种相交形状。如图3所示,根据平面与圆柱的位置关系,剖面相交形状可分为以下3类。 图3 平面与圆柱相交情况 2.3.1 圆柱颗粒撕裂面 当剖面是撕裂面时,圆柱颗粒偏向剖面的一侧,另一侧的相对位置上会产生空腔,其原理与球类似。对于目标点P(x,y,z), 该点处剖面的单位法线向量为Nc,圆柱底面圆心为O,高度为height,圆柱从底面到顶面的轴向为D。算法遍历相邻的27个圆柱,判断点P是否在某个圆柱内。首先根据式(11)计算底面圆心O到点P的向量M在轴向D上的投影长度l l=(P-O)·D (11) 如果l<0或l>height,则说明点P不在圆柱高度范围内,停止遍历;否则继续判断不等式(12),当不等式成立时,说明点P不在圆柱内,点P处的法线没有扰动 M·M-l2>R2 (12) 当不等式(12)不成立时,则说明P在该圆柱内,需要进一步计算扰动的法线。如图4所示,在P点分别沿T=Nc的方向与T=-Nc的方向发出一条射线与圆柱交于一点,交点记为Q1和Q2。当交点在圆柱的侧面上时,如图4(a)所示,令 (13) 解方程(13),可得交点距离P点的距离为 (14) 当交点在圆柱底面上时,如图4(b)所示,令:M=P-O,交点距离P点的距离为 (15) 对于T=Nc和T=-Nc的方向均取距离的非负根,然后将两个交点返回的距离值v,w进行比较,距离值较大的一侧即为圆柱偏向的一侧。 图4 撕裂面圆柱倾向判断 当圆柱偏向T=Nc方向一侧时,根据返回的距离值v,求得沿T=Nc方向与圆柱交点Q1的坐标,然后根据下式计算P点到底面圆的垂直距离s以及P点对应圆面的圆心O′ (16) 取Q1点指向圆心O′的向量作为扰动后的法线Nq Nq=(O′-Q1)/|O′-Q1| (17) 当圆柱偏向T=-Nc方向一侧时,根据返回的距离值w,求得沿T=-Nc方向与圆柱交点Q2的坐标,同理使用式(16)计算得到P点到底面圆的垂直距离s以及P点对应圆面的圆心O′,最后取圆心O′指向Q2点的向量作为扰动后的法线Nq Nq=(Q2-O′)/|Q2-O′| (18) 2.3.2 圆柱颗粒空心切割面 在剖面是切割面情况下,与剖面相交的圆柱被切为两半。对空心切割面情况,法线计算方法与撕裂面情况相似。区别是对于空心切割面,只需判断任意一点P是否落在圆柱内,而不用判断圆柱偏向剖面的哪一侧。在P落在某个圆柱内时,使用沿T=-Nc方向与圆柱相交的方法计算扰动的法线,如式(18)。 2.3.3 圆柱颗粒实心切割面 在剖面为实心切割面情况下,由于圆柱与剖面相交会产生各种不同的截面形状,本文将圆柱外部的部分向内缩小一段距离t,使其与剖面相交的截面显示出来,以模拟出不同形状的凹凸映射效果。如图5所示,算法首先遍历与P点相邻的27个圆柱,对每个圆柱,判断P是否在圆柱内。如果是,停止遍历,否则计算底面圆心O到点P的向量在D上的投影长度l,从而判断圆柱与剖面相交关系。 图5 圆柱实心切割面扰动法线计算方法 当l<0或l>height时,则说明圆柱与剖面不相交,否则相交。在相交条件下,根据下式计算P点处对应的圆形截面的圆心O′以及P到圆柱面的距离dc (19) 当算法遍历结束后,任意一点P与圆柱的位置关系有以下3种情况: (1)P落在某个圆柱之内; (2)P不在任何圆柱之内,没有圆柱与剖面相交; (3)P不在任何圆柱之内,有圆柱与剖面相交。 对于(1)和(2),P点的法线向量就是Nc,没有扰动。对于(3),取dc值中的最小值dmin,dmin对应的圆心为O′min, 当dmin>t(阈值t为圆柱向内缩进的距离,取值为圆柱间距值的0.07倍)时,P点的法线向量仍然是Nc,没有扰动。否则,通过下式计算从O′min指向P的单位向量B B=(P-O′min)/|P-O′min| (20) 则扰动后的法线Nq为 Nq=(N+B)/|N+B| (21) 本文实验中,仿真程序使用C++编写,三维图形渲染使用OpenGL函数库,程序式凹凸映射生成算法使用OpenGL着色语言(Shader)编写。运行硬件环境配置为:Intel i7-3770 CPU,8 GB内存;2 GB显存的NVIDIA GeForce GTX 750 Ti GPU。 在仿真实验1中,本文模拟了内部微观结构为球时的剖面渲染效果。图6展示了斯坦福兔子模型(长20 cm,宽16 cm,高20 cm)在剖面法线为(1,0,1)、球间距初值为0.6、球半径初值为0.3时的渲染效果。 图6 斯坦福兔子模型剖面渲染效果,法线为(1,0,1) 从实验结果(图6)可以看出,撕裂面上一侧的凸起,在另一侧的相对位置是凹陷,反之亦然,并且两侧剖面效果互补;对于空心切割面,两侧均为凹陷;实心切割面两侧均为圆形切割形状。并且对内部球使用三维噪声扰动后,球的位置、大小均显现出不规则性,效果与预期相符。实验结果说明该算法可以有效地模拟内部球形微观颗粒,同时可以在剖面上有效实现程序式的凹凸映射。 通过仿真实验2可以验证本文算法对任意法线剖面的渲染效果,并且将同一模型在不同法线的剖面和内部微观结构间距、大小均不相同的情况进行对比,如图7所示。图7展示了斯坦福兔子模型在剖面法线为(1,1,1)、球间距初值为0.5、球半径初值为0.25时的渲染效果。与图6的实验结果相比,可以发现这两个不同法线剖面的渲染效果相似,均具有不规则性和一致性,由此说明本文的算法适用于任意法线的剖面。 图7 斯坦福兔子模型剖面渲染效果,法线为(1,1,1) 仿真实验3测试本文算法对不同模型的适用性。本实验选取多个模型,针对不同模型使用不同的剖面进行效果展示。图8展示了鹿模型(长15 cm,宽5 cm,高13 cm)在剖面法线为(0,0,1)、球间距为0.3、半径为0.15时的渲染效果。渲染效果与前面情况类似,符合预期结果。实验结果说明,本文提出的算法对不同的模型剖面均具有较好的模拟效果。 图8 鹿模型剖面渲染效果,法线为(0,0,1) 圆柱与剖面相交会产生多种形状,仿真实验4首先模拟圆柱方向相同且方向为(0,0,1)时的剖面渲染效果。实验选用斯坦福兔子模型,内部圆柱间隔为1.0,圆柱高度为0.8,圆柱底面圆的半径为0.5。图9展示了不同法线下撕裂面的渲染效果。图10展示不同法线下空心切割面渲染效果,图11展示了不同法线下实心切割面渲染效果。 图9 不同法线下的撕裂面渲染效果 图10 不同法线下的空心切割面渲染效果 图11 不同法线下的实心切割面渲染效果 从图9、图10、图11中可以看出,当剖面法线为(0,0,1)时,剖面与圆柱底面平行,产生的剖面形状为大小不同的圆形。当法线为(0,1,0)时,剖面与圆柱底面垂直,剖面形状为大小不同的长方形。当剖面法线为(1,1,1)时,剖面与圆柱相交产生大小不同的椭圆形、鼓形等其它各种形状。其中撕裂面上既有凸起也有凹陷,且两侧效果互补;空心切割面两侧均为凹陷;实心切割面均是相交截面的形状的显示。以上结果可以验证本文提出的算法对不同法线的剖面都具有良好的凹凸映射结果。 上述实验中只使用三维噪声对圆柱的半径、高度和位置进行扰动,并未对圆柱的方向进行扰动。为了更真实地模拟实际情况,本实验使用三维噪声对圆柱的方向进行扰动,从而得到方向不同的圆柱。图12展示了内部圆柱间隔为0.8、圆柱高度为0.7、圆柱底面圆的半径为0.4、剖面法线为(0,1,0)条件下的不同剖面渲染效果。实验结果可以看出,对圆柱方向扰动后,在同一剖面上,会同时出现多种相交形状,这说明噪声扰动后的圆柱具有各向异性,同一剖面上可以同时产生多种形状,因此剖面渲染的结果更具有真实感。 如表1和表2所示,本文对同一模型不同微观结构剖面渲染所需时间和不同模型不同微观结构剖面渲染所需时间进行分析与对比。表1对比了在内部微观结构不同、渲染帧数不同的情况下,斯坦福兔子模型渲染所需要的时间和平均每帧所需的时间。由该表可知:①在渲染帧数较少(如200、500)的条件下,平均一帧所用时间较多,这主要由于程序启动和结束过程占用较多的时间;②随着渲染帧数增加,平均每帧所用时间减少,当渲染帧数达到1000帧时,渲染一帧画面所用时间趋于稳定,为0.5 ms左右。 如表2所示,本文对比了不同模型渲染不同帧数的画面时所用的时间和平均每帧所用时间。由该表可知,对于不同模型,在内部模型间距、大小不同的情况下,渲染一帧所需的时间也较为稳定。 综上所述,针对同一模型不同微观结构与不同模型不同微观结构,本文提出的算法在运行时间方面表现较为稳定,因此在切割时,可以满足实时切割渲染的要求。 本文提出一种在三维模型任意剖面上生成凹凸映射效果的程序式算法。为提高剖面模拟效果,该算法使用Perlin噪声对模型内部规则的球、圆柱等颗粒进行扰动,以生成不规则的微观结构。并根据剖面与微观结构的位置关系,将剖面分为撕裂面、空心切割面、实心切割面3类,针对不同剖面应用不同的程序式凹凸映射生成算法进行渲染,得到剖面的凹凸映射纹理。仿真实验结果表明,本文提出的算法可以针对三维模型的任意剖面进行凹凸映射,并有良好的映射结果;同时,剖面渲染时间较短,可以应用于对实时切割渲染要求较高的场景。未来的工作中拟使用形状复杂的颗粒和更复杂的随机分布算法模拟三维模型内部微观结构,最大程度上提高剖面模拟效果。并结合碰撞检测算法,来避免颗粒间相互重叠的现象,以达到更准确的凹凸映射效果。 表2 不同模型不同微观结构剖面渲染所需时间2.3 圆柱颗粒剖面算法

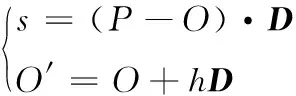
3 实验结果与分析
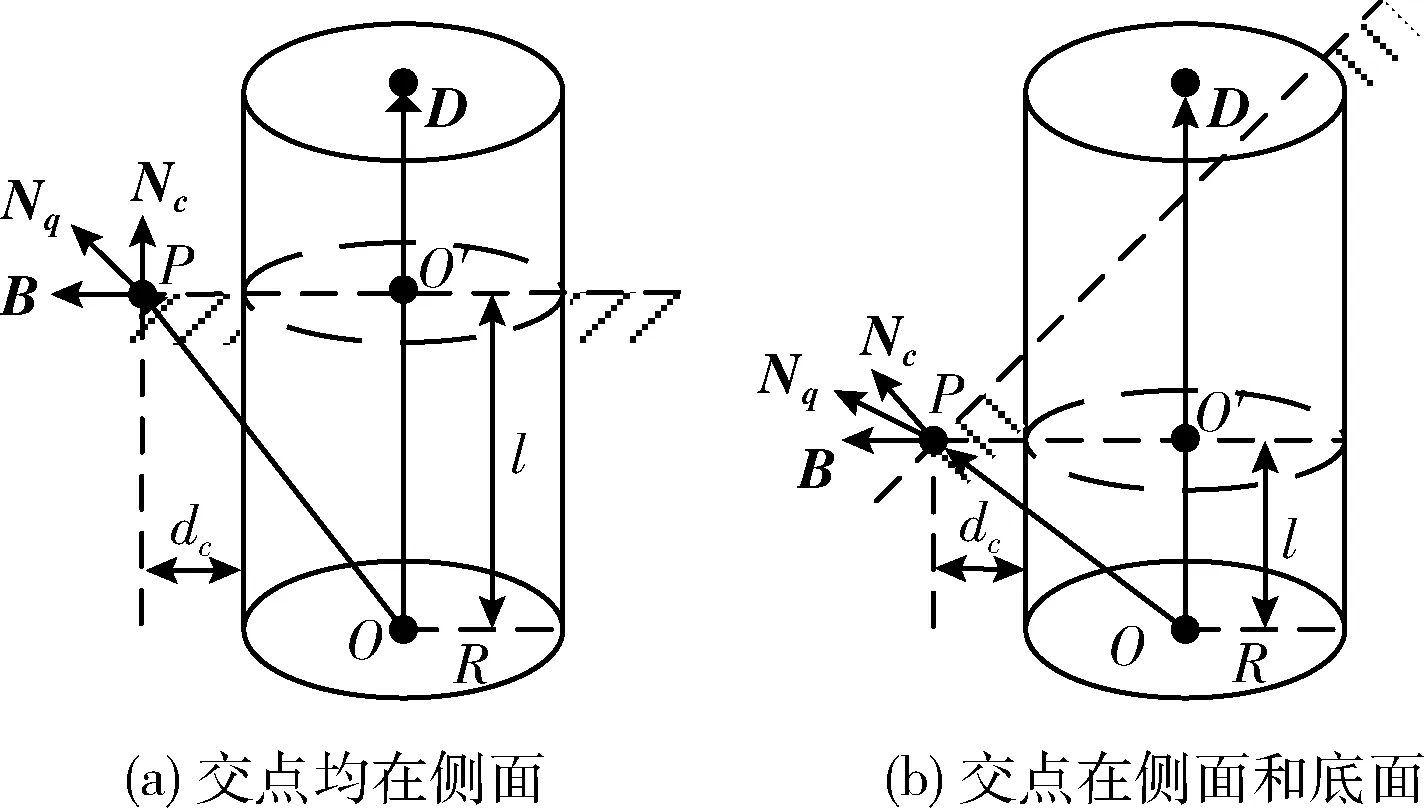
3.1 微观结构为球时凹凸映射结果

3.2 微观结构为圆柱时凹凸映射结果
3.3 运行时间分析
4 结束语


