不平衡数据中基于权重的边界混合采样
姜新盈,江开忠,严 涛,王舒梵
(上海工程技术大学 数理与统计学院,上海 201620)
0 引 言
各个类别样本数量相差较大的数据集称为不平衡数据,不平衡数据在各个领域中随处可见,如工业故障检测[1]、疾病诊断[2]、信贷欺诈[3]、石油储层含油量识别[4]等,因为少数类样本的存在,传统分类方法为了确保得到较高的整体分类性能会向多数类倾斜,这也导致少数样本分类错误[5],但是,人们经常关注分类错误成本较高的少数类样本。因此,如何确保多数类样本准确性的同时提高少数类样本的识别精度是机器学习中需要解决的一大难题。
现有文献中仅使用欠采样或过采样算法会产生过拟合问题或者误删重要样本,而混合采样算法的分类效果一般比单一的采样方法好[6]。许多研究学者相继提出混合采样方法。侯贝贝等[7]提出的BMRM算法以及吴艺凡等[8]提出的SVM_HS算法虽然区分了不同类别样本,但合成样本质量不佳,陆万荣等[9]改进的MD-SMOTE算法虽然改善了少数类样本分布边缘化问题,但存在易产生冗余样本的风险。
以上算法大部分没有区分少数类样本的重要性,且没有考虑类内分布情况,针对以上问题,本文提出了BWBMS算法来更有效识别少数类样本。一方面考虑类内样本分布情况,通过引入边界因子将数据集划分成边界集和非边界集,再设置采样比重和总权重将边界集少数类样本进行划分,考虑不同位置少数类样本的重要性,分别采用不同的采样算法和采样倍率,使得在远离边界的密集区域的样本合成较少,在靠近边界的低密度区域的样本合成较多。另一方面,考虑不同区域样本的不同,对非边界集中的多数类样本采用NearMiss1算法[10]进行删减,最终使类别样本集相对平衡。
1 相关工作
1.1 不平衡数据分类问题
在当前研究中,主要从以下3类研究非平衡数据分类:在特征层面,主要是筛选原始特征或构造新特征来有效识别少数类;从算法层面来看,主要是利用代价敏感因子等对现有的算法改进,如使用单一样本来训练的单类学习、把多个基分类器的分类结果进行集成的集成学习[11]、引入代价的代价敏感学习[12]等。在数据层面,主要是通过欠采样、过采样以及混合采样来平衡数据集以提升分类性能。
欠采样算法中较为典型的是随机欠采样,但是极易误删重要样本,基于此,吴圆圆等[13]根据样本间的欧氏距离和k近邻规则来删减多数类样本。而过采样算法中经典的SMOTE算法[14]也有一些问题:容易受到噪声样本影响而造成合成样本质量不佳;没有对少数类样本区别对待,且容易导致两类样本边界模糊;未注意到少数类样本的分布情况,容易在密集区产生过多样本;合成样本仅进行线性插值,导致样本分布区域小而使分类器易过拟合[6]。为了改善SMOTE的缺点,Wang等[15]使用Random-Smote算法,少数类样本在三角形内进行插值,使合成样本的分布更加合理,但没有对少数类样本细分;古平等[16]对细分的少数类样本采用不同的过采样方法,但没有注意到少数类样本分布问题。赵清华等[17]使生成样本接近于质心,降低了合成样本分布位于边缘的可能性,也改善了样本数据集分布问题,但没有关注到少数类样本的区别。这些算法仅对少数类进行处理,分类性能有所不足。
1.2 相关采样算法
1.2.1 SMOTE算法
SMOTE算法[14]流程如下:
(1)计算少数类样本集C(1)中每个个体x到C(1)中所有个体间的欧式距离,计算每个少数类个体x的k近邻;
(2)循环选择少数类样本集C(1)中的个体x, 随机选择其k近邻样本点作为辅助样本y;
(3)在根样本x和辅助样本y之间按照以下公式进行新样本的合成
xnew=x+rand(0,1)×|x-y|
(1)
1.2.2 Random-SMOTE算法
Random-SMOTE[15]是在三角形区域内进行线性插值以形成新的样本,其算法流程如下:
(1)根据样本的不平衡比例设置一个采样倍率,从少数类样本集C(1)中循环选取个体x, 在k个同类近邻中选择两个样本点y1、y2作为间接样本。根据以下公式在y1、y2之间进行随机线性插值,生成N个间接样本pj,j=1,2,……,N
pj=y1+rand(0,1)×(y2-y1)
(2)
(2)在pj和x之间根据下列公式进行线性插值以构造新的少数类样本
xnew=x+rand(0,1)×(pj-x)
(3)
2 BWBMS算法
BWBMS算法是把欠采样和过采样算法思想结合起来所提出的算法,主要创新点在于考虑了边界集中少数类不同位置样本的重要程度的不同,所使用的采样方法和采样倍率是依据样本的位置及其所处位置的稀疏程度而定,另一方面考虑类内样本的稀疏程度,计算边界集少数类样本集中每个个体的支持度和密度,并赋予各个样本相应权重,对少数类样本根据密度权重和支持度权重之和以及采样比重进行细分,避免在密集区生成大量冗余样本,稀疏区依旧样本较少。最后在非边界集采用NearMiss1欠采样算法来处理多数类样本,保留对分类起重要作用的样本,以使类别样本集相对平衡。
2.1 数据集边界因子
根据支持向量机(SVM)的原理,样本离类别边界越近,其包含的重要信息就越多,直接删除边界上的样本点有可能会误删含有重要信息的样本[7],因此有效识别出边界点对于提高少数类分类精度是极其重要的。
为了有效识别出边界点,文中引入k-离群度[9]来有效识别边界点,将原样本空间划分为边界集和非边界集,具体定义如下:
定义1k距离:对于数据集M和任意正整数k, 对象x的k距离记为dk(x), 其中对象x∈M且满足:
(1)至少有k个对象y∈M-{x}, 使得
d(x,y)≤dk(x)
(2)至多有k-1个对象y∈M-{x}, 使得
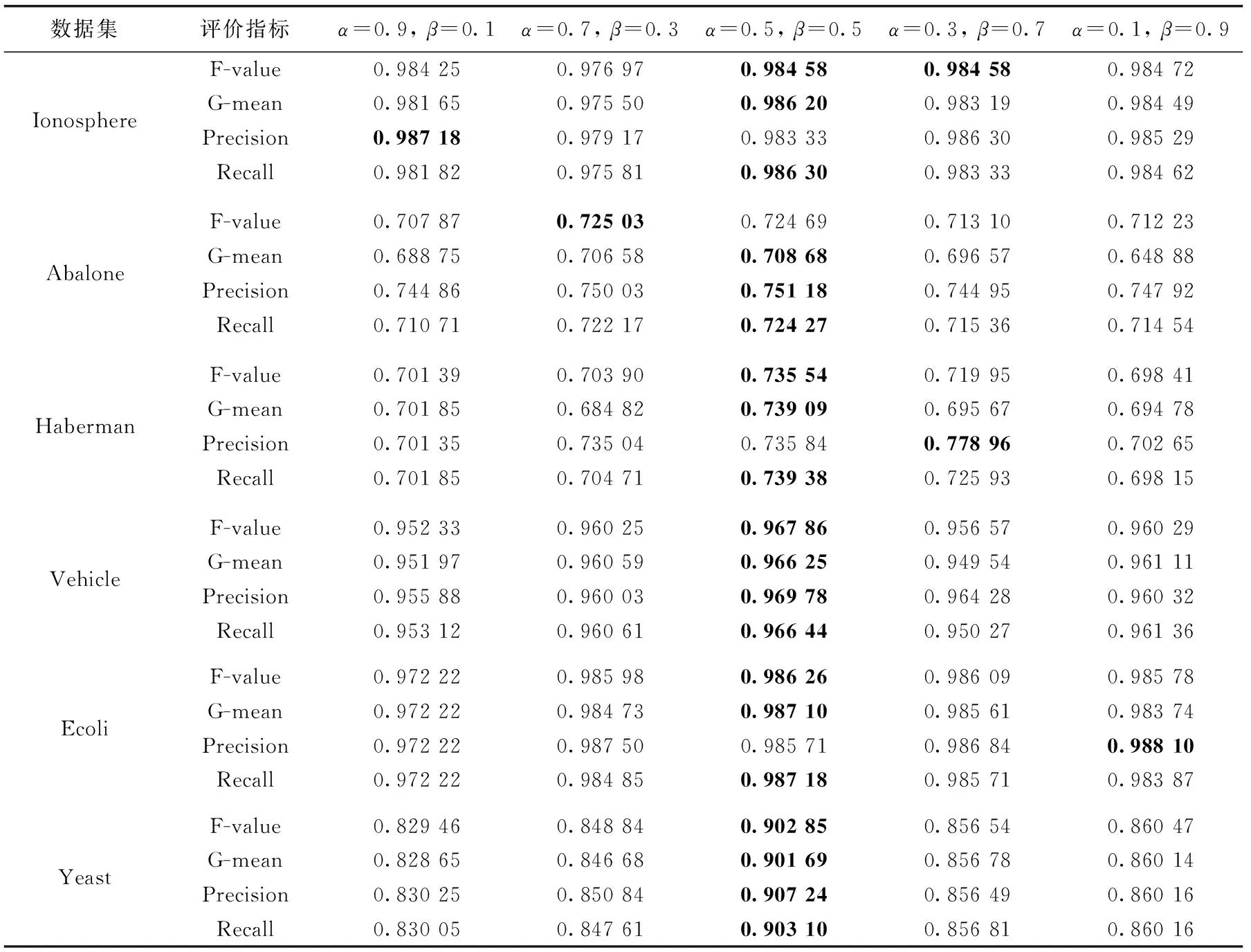
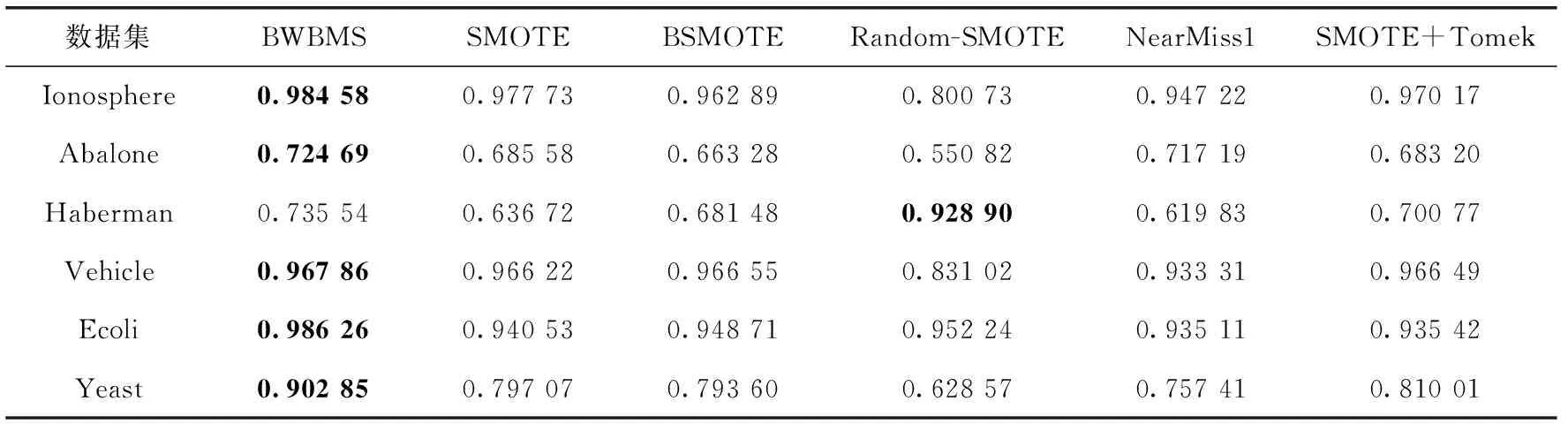
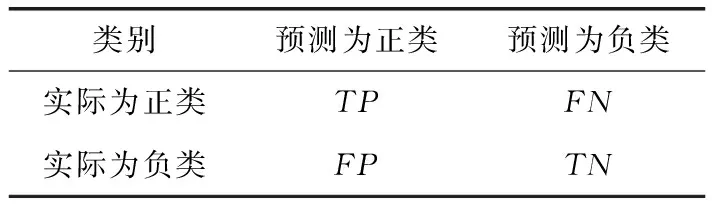
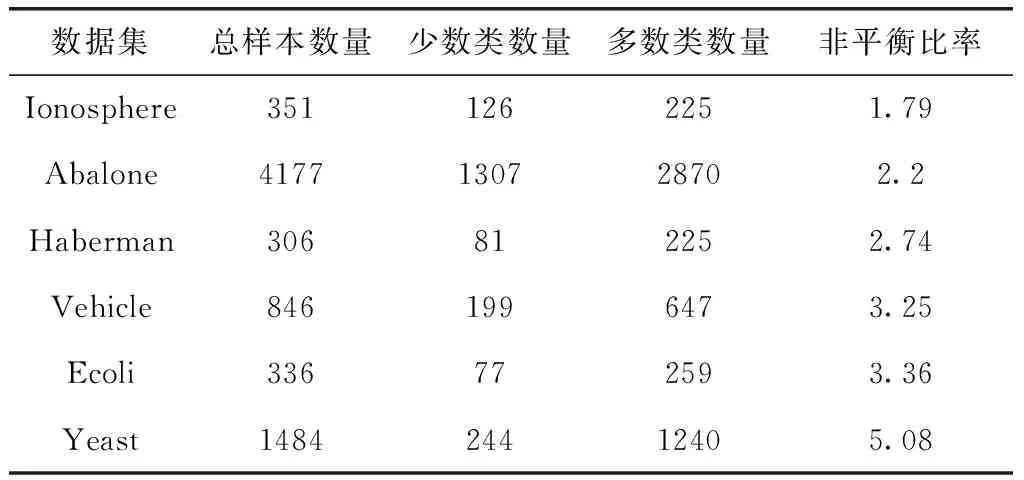
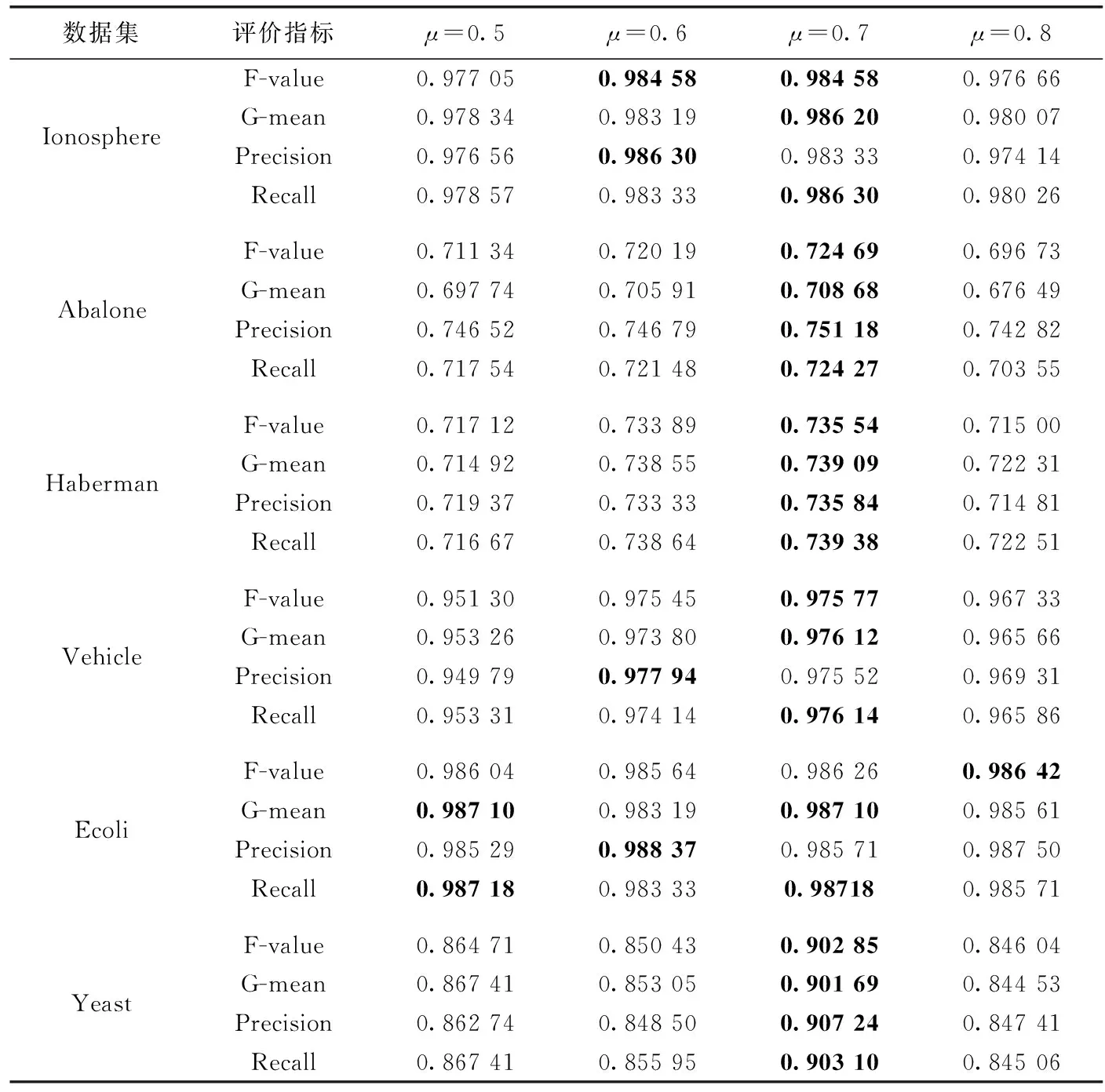
d(x,y) 其中,d(x,y) 表示x与y之间的欧氏距离。 定义2k-离群度:对任意点x∈M,x的k距离与其ε邻域内所有点(包含x)的k距离的平均值之比,称为x的k-离群度,记为 (4) 其中, |ε(x)| 为点x的ε邻域内样本点的个数。(下同)特殊地,本文取ε=dk(x),x的ε邻域等于x的k近邻邻域。 定义3 边界因子:数据集M中任意点x的k-离群度与1之差的绝对值记为点x的边界因子σ(x)。 即 σ(x)=|1-τ(x)| (5) 边界因子的大小反映了该点周围样本的分布,根据以上定义,可以通过设置阈值σ0并与σ(x) 进行比较来判断样本点是否为边界点。 定义4 边界点:对于任意x∈M, 当σ(x)>σ0时,称样本点x为边界点,否则为非边界点。其中 (6) (7) (8) 则样本x的密度权重为 (9) 总权重公式为 w(x)=α*wρ(x)+β*wk(x) (10) 为了提高算法整体运行速度,并使数据样本的分布越来越合理化、均匀化,应选择适当的欠采样算法。在去除原始数据集的噪声之后,本文采用基于数据分布特征的NearMiss1算法[10]来处理非边界集中的多数类样本,计算每个多数类样本点的k个异类最近邻,保留到最近的这k个异类最近邻平均距离小的点,以此降低算法复杂度并能保留含有重要信息的样本点。 输入:原始数据集C=C(0)∪C(1)且C(0)∩C(1)=∅ (C(0): 多数类样本集,C(1): 少数类样本集近邻参数k, 边界阈值σ0) 输出:均衡数据集Cnew 步骤1 对于数据集C中的每个个体x, 计算对应的k近邻,如果这k个近邻样本全部为异类样本,就把个体x视为噪声样本,从C中剔除,得到C′, 其样本量为 |C′|。 步骤2 fori=1 to |C′|, 计算C′中每个样本x的边界因子σ(x); 步骤2.1 计算样本点x到其它样本点的欧氏距离,得到对应的k距离dk(x); 步骤2.2 计算每个样本点的k-离群度τ(x); 步骤2.3 计算每个样本点的边界因子σ(x)。 对于不平衡数据的研究,正确的区分出误分代价更高的正类是当前机器学习的目标。但是仅使用准确性作为评估指标是不公平的,研究学者常常根据混淆矩阵引入的概念来评估算法性能。表1是二分类问题的混淆矩阵。 表1 混淆矩阵 根据混淆矩阵,引入查全率、查准率和真负率3个定义。 查全率(Recall)是指数据集中正类样本被预测正确的比率 (11) 查准率(Precision)是指所有预测为正类的样本中,实际上也是正类的比率 (12) 真负率(TNR)是指所有真负类样本中被预测为负类的比率 (13) 由于传统评价指标对少数类的不公平性,F-value作为新的评价指标被提出,其既考虑了准确率,又考虑了召回率,公式如下 (14) G-mean是另一种评价分类性能好坏的指标,当R值和TNR值同时变大时,G-mean值才会越高。公式如下 (15) 本文主要使用F-value、G-mean、Precision、Recall这几个指标来衡量算法的分类性能。 本文从国际机器学习标准库UCI中选取了Ionosphere、Abalone、Haberman、Vehicle、Ecoli、Yeast这6组不平衡数据集,来验证所提算法的有效性。本文重在研究不平衡数据的二分类问题,将多数类数据集重构为不平衡的二分类数据集。其中对于Abalone数据集中标签为“F”的样本定义为少数类,其它类别合起来为多数类;Vehicle数据集中,将第一类视为少数类,其它均为多数类;Ecoli数据集中将“om”、”omL”和“pp”合并为少数类,其它类归为多数类;Yeast数据集中将“MIT”视为少数类,其它为多数类。6组数据集的具体信息见表2。 表2 数据集信息 为了验证本文所提算法BWBMS算法的有效性,选取SMOTE算法、Borderline-SMOTE算法(BSMOTE)、Random-SMOTE算法、NearMiss1算法、SMOTE+Tomek Links算法在8组数据集上做对比实验,并选取SVM作为分类器,用F-value、G-mean、Precision和Recall作为评价指标进行对比。实验环境基于Anaconda 3.0中Jupyter Notebook软件,所使用的对比算法除Random-SMOTE外均调用该软件中imbalanced-learn程序包实现。经过反复的大量实验得出参数k=8, 其它参数通过接下来的参数敏感性分析进行选择。 3.3.1 参数敏感性分析 本文所提的BWBMS算法需要确定采样比重μ、 密度权重系数α和支持度权重系数β。 在此选取了6组公开数据集进行实验,并以SVM为分类器,其中SVM的各参数均为Scikit-learn程序包的默认参数。此外用F-value、G-mean、Precision和Recall来评估各参数的影响。为了评估采样比重μ的影响,对μ分别设置为0.5、0.6、0.7、0.8进行实验,从表3可以看出,当μ=0.7时,各指标普遍表现较好。 密度权重系数α和支持度权重系数β分别表示密度权重和支持度权重在样本选择时的重要性,当α和β越大时,说明稀疏区域且离边界近的样本更为重要,当两者相等时,认为密度权重和支持度权重一样重要。下面设置了几组对比实验来评估不同权重系数值的影响。其中,设置μ=0.7, 且将 (α,β) 设置为(0.9,0.1),(0.7,0.3),(0.5,0.5),(0.3,0.7),(0.1,0.9)这5组分别进行实验以选取更好的参数。实验结果见表4,由此可知,当α=β=0.5时,6组数据集上的各指标整体性能表现较好。 表3 不同采样比重μ下分类效果对比 3.3.2 实验结果 根据前面的实验对比,本文将实验参数设置如下:k=8,μ=0.7,α=β=0.5, SVM分类器中的参数都是Scikit-learn程序包中的默认参数。表5和表6展示了6组数据集在本文采样方法和其它采样算法结合SVM分类器上的F-value值和G-mean值,实验结果的最大值用黑色粗体表示。 从表5可以看出BWBMS算法在提高少数类分类精度上较为有效,大部分数据集在经过本文所提出算法的处理再结合SVM分类器后,评价指标值都高于文中其它采样算法组合形式,这是因为BWBMS算法处理数据时,首先去除了噪声样本,能提高合成样本质量,再对边界集中的少数类和多数类样本作相应的处理,赋予样本支持度权重和密度权重,根据每个少数类样本的重要程度采用不同的采样方法和采样倍率,在一定程度上降低了错分边界点而造成的不利影响,避免在样本密集区继续生成大量冗余样本,虽然在Haberman数据集上的F-value值没有取得最优值,但较有些算法的F-value都有所提升。 从表6可以看出,BWBMS算法在Abalone和Vehicle数据集上的G-mean值没有取得最优值,但与其它算法相差不大。结合表5和表6来看,对Haberman数据集使用Random-SMOTE算法的结果优于本文算法结果,这是由于Haberman数据集的边界点重叠度较大,本文引入的边界因子概念以及该算法设置的边界阈值对于边界点重叠较大的数据集可能有点不足,而使得三角形插值的Random-SMOTE算法更适合这个数据集。但是从整体上来看, BWBMS算法在提高少数类分类精度上优于文中所提其它对比算法。 图1绘制了6种算法在不同数据集上的打分情况变化曲线。其中,纵坐标分别代表F-value、G-mean、Precision、Recall这4个评价指标,表示分类得分情况,取值范围为0-1,横坐标列举了6种实验对比算法。综上可知,BWBMS算法优于文中所对比的其它算法。 本文提出了不平衡数据中基于权重选择的边界混合采样算法,既考虑了不同区域样本重要性不同,又考虑了类内样本分布情况。将BWBMS算法与SVM分类器结合在一起,并与5种采样算法进行实验对比,该算法在大部分UCI公开数据集上表现较好,F-value、G-mean、Precision和Recall这4个评价指标有所提升,验证了该算法的有效性,可将该算法推广至现实领域中来处理不平衡数据。未来,一方面研究更佳的边界阈值的选取,另一方面本文仅结合了SVM分类器,将不同改进的分类算法与BWBMS相结合会产生什么样的分类效果也是今后的研究方向。 表4 不同权重系数(α,β)下分类效果 表5 不同数据集在不同算法上的F-value性能对比 表6 不同数据集在不同算法上的G-mean性能对比 图1 6种算法在不同数据集上的打分情况2.2 基于边界因子的边界集识别

2.3 对边界集少数类样本的处理


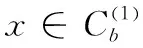
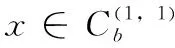
2.4 非边界集样本的处理
2.5 BWBMS算法描述
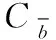


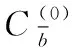

3 实验及结果分析
3.1 评价指标
3.2 数据集描述
3.3 实验及分析
4 结束语