发动机支架焊接结构疲劳寿命预测

隋鹏超,刘宏杰，曾超

1.内燃机可靠性国家重点实验室，山东潍坊 261061; 2.潍柴动力股份有限公司，山东潍坊 261061

0 引言

焊接结构失效以焊接接头的疲劳损伤为主[1]。由于焊接接头具有几何不连续、焊接缺陷、局部残余应力等特殊性，以及焊接工艺引起的局部材料性能分布不均，焊接疲劳分析面临2个难题：1) 网格敏感性问题[2]，即难以对焊接接头的应力集中状态进行准确求解；2)焊接接头准确分类问题，即实际工程应用中的疲劳S-N曲线选择问题[3]。

解决网格敏感性和焊接接头准确分类问题可采用名义应力法、结构应力法(热点应力法)和缺口应力法。名义应力法和热点应力法需要对焊接接头进行详细分类[4]，包括接头的几何形状和特定的载荷模式，英国和国际焊接学会的相关标准均给出了几十种接头的具体形式，并通过标准化作业，在机车、船舶、压力容器等行业有所应用，但是仍无法覆盖工程应用中种类繁多的焊接接头和复杂多变的工作载荷；文献[5-6]提出的结构应力法和主S-N曲线法是目前比较可靠的焊接疲劳寿命评估方法，2007年编入美国机械工程师协会标准，在国内也有一定的应用；名义应力法和热点应力法没有详细考虑焊接接头在焊根和焊趾位置的几何特征，不能真实反映焊缝周围的应力-应变状态[7-9]；结构应力法通常采用公式外推法估算焊接接头的应力状态，但焊趾和焊根缺口处具有较强的网格敏感性，容易导致局部应力奇异。缺口应力法[10-11]是焊接疲劳分析的一种局部方法，旨在获取缺口应力的疲劳数据，进一步提高焊接结构疲劳分析的准确性。

文献[12]简称FKM标准，由德国机械工程研究委员会编写。FKM标准主要采用结构应力法和主S-N曲线法，但同时考虑了缺口应力。本文中以发动机消音器焊接支架为例，探讨FKM标准在焊接结构疲劳分析中的具体应用，根据准静态多通道疲劳分析法，以发动机多体动力学计算载荷时间历程，构造实际疲劳载荷谱，实现在产品设计初期评估焊接结构的疲劳寿命。

1 焊接结构疲劳分析方法

1.1 等效结构应力法

焊接结构的焊趾位置通常为应力集中区域，无法应用有限元法准确求解，但是焊趾处的节点力和节点力矩是准确的。结构应力法根据力平衡原理，将节点载荷变换为单元边的线载荷，应用结构应力分解，实现网格不敏感。

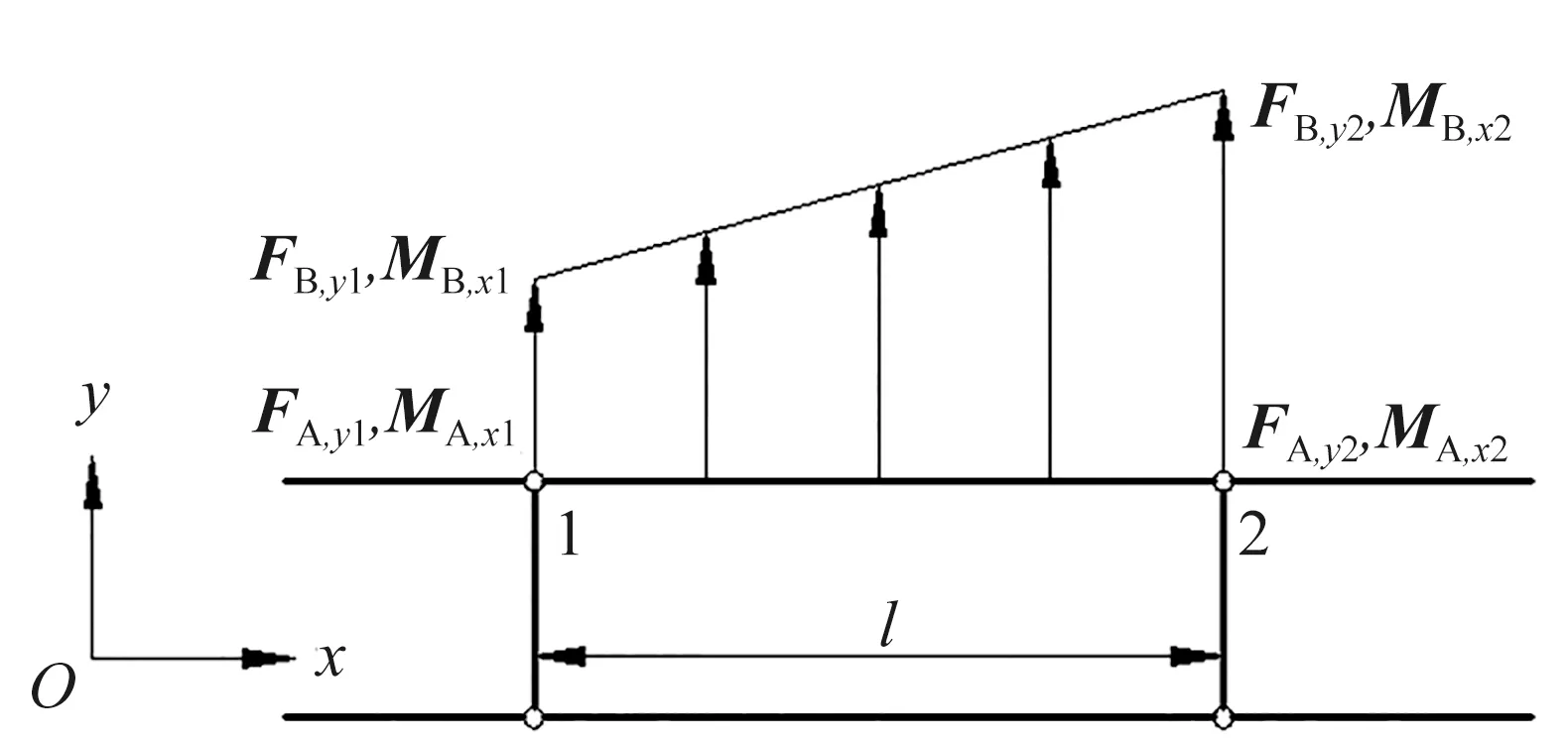
图1 2个节点的节点力和线力分布

1.1.1 节点力和线力的转换

2个节点的节点力和线力分布如图1所示。在局部平面坐标系下，节点1和节点2在y轴的节点力及绕x轴的节点力矩分别为FA,y1、FA,y2和MA,x1、MA,x2，y轴方向的线力及绕x轴的线力矩分别为FB,y1、FB,y2和MB,x1、MB,x2，单元长度为l。根据节点载荷与线载荷的平衡原理，得到线力和线力矩方程为：

式中：L为等效转换矩阵，只与节点长度l相关，对于一段由n个单元连接而成的焊缝，

1.1.2 结构应力分解

焊趾处的应力分布如图2所示，图中d为板厚，τ(y)为焊趾处剪切应力。外力作用下，因为缺口应力的存在，焊缝焊趾处的应力沿着焊趾在厚度方向上呈现高度的非线性分布。将焊趾处的总应力σ(x)定义为膜应力σm、弯曲应力σb和非线性的缺口应力σp之和，缺口应力σp是自平衡的残余应力。结构应力σs为膜应力与弯曲应力之和，对焊接结构的疲劳性能起主要作用，且一定与外力平衡。

图2 焊趾处的应力分布

式中：Fy为焊缝单位长度的线力，N/mm；和Mx为焊缝单位长度的线力矩，N·m。

与名义应力、热点应力不同，结构应力的物理意义明确，即基于力的平衡，在已知的外力作用下，无论焊缝上节点力有多少，都会与外力平衡，从而实现对有限元网格的不敏感。焊趾处的应力分解是极为关键的核心技术。

1.2 主S-N曲线法

焊接接头存在微小裂纹，是焊接结构疲劳失效的根源，因此应用断裂力学理论对焊接结构疲劳进行研究，假设焊趾处的微小裂纹在受到外力作用之前已经客观存在。

对于几何形状不同的焊接接头，其S-N曲线在寿命区间内分布在同一窄带上。主S-N曲线法将结构应力变化范围Δ(σs)、d和载荷加载模式I(r)这3个参数定义为等效结构应力幅

(1)

对式(1)进行变换，得到基于等效结构应力幅的主S-N曲线：

Δ(Ss)=CdNh

式中：N为焊接结构疲劳寿命，次；Cd和h为试验常数。

2 焊接结构疲劳评估的FKM标准

2.1 缺口应力

结构应力法不适用于评估由起始于焊根的焊接微裂纹缺陷导致的疲劳失效情形。FKM标准以结构应力为基础，通过缺口应力法计算焊根和焊趾的缺口系数，进而定义焊接接头的缺口应力，再应用主S-N曲线，对焊缝的疲劳性能进行评估。

缺口应力计算示意图如图3所示,图中d1、d2为板厚，mm。对于T型单边焊的焊接接头，需评估的焊缝焊趾单元E1的上表面的缺口应力

式中：β1、β2和β3分别为垂直于焊缝方向的拉压工况、弯曲工况、相邻单元的缺口系数；σb,top为结构应力在焊趾上表面的弯曲应力分量，Pa；σm为焊趾结构应力的膜应力分量，Pa；Fa和Fn分别为E1及其相邻焊趾单元E2的缺口应力分量，Pa，Fa=(σs,top,E1+σs,bot,E1)t1，Fn=(σs,top,E2+σs,bot,E2)t2，其中σs,top,E1、σs,bot,E1、σs,top,E2、σs,bot,E2分别为E1、E2的上、下表面的结构应力，Pa。

图3 缺口应力计算示意图

2.2 缺口系数

根据文献[11]提出的虚拟缺口半径法，考虑焊接接头的三维几何形状，通过有限元子模型确定缺口系数。焊接接头的子模型如图4所示，焊趾和焊根几何缺口简化为半径为1 mm的圆角，同时定义焊缝厚度为a；焊缝坡角为b；熔深率为η，η=(t2/D)sinc，其中c为焊接板材的夹角，对于T型焊接接头，c=90°。

焊接接头的拉伸、弯曲等载荷工况如图5a)所示，通过有限元法计算焊接接头的焊根和焊趾在单位力F或单位力矩M作用下的应力分布，结果如图5b)所示。

缺口系数由焊根和焊趾的最大主应力计算得到，焊根的缺口系数

βt=σt/σ∞，

(2)

式中：σt为焊根的最大主应力，Pa；σ∞为板材远场的最大主应力，Pa。

图4 缺口应力计算示意图 图5 焊接接头载荷工况和应力分布示意图

焊趾的缺口系数

(8)

式中：σr为焊趾的最大主应力，Pa；σtop、σbot为板材顶面、底面的最大主应力，Pa。

3 准静态多通道疲劳分析法

准静态多通道法焊结构疲劳分析流程如图6所示。准静态多通道法根据线性载荷叠加原理，由单位激励载荷作用下的应力分布与实际载荷时间历程的乘积作为疲劳分析的载荷谱。实际载荷时间历程由发动机多体动力学计算得到，可在没有样机的产品开发中，通过完全正向求解得到发动机及其零部件的动力学响应，可以不必依赖于样机的测试，可以缩短开发周期，降低成本。单位载荷作用下的应力求解采用惯性释放法，具有模型规模小、对计算资源要求低等优点，而且采用同一应力分布结果，可进行多事件分析。

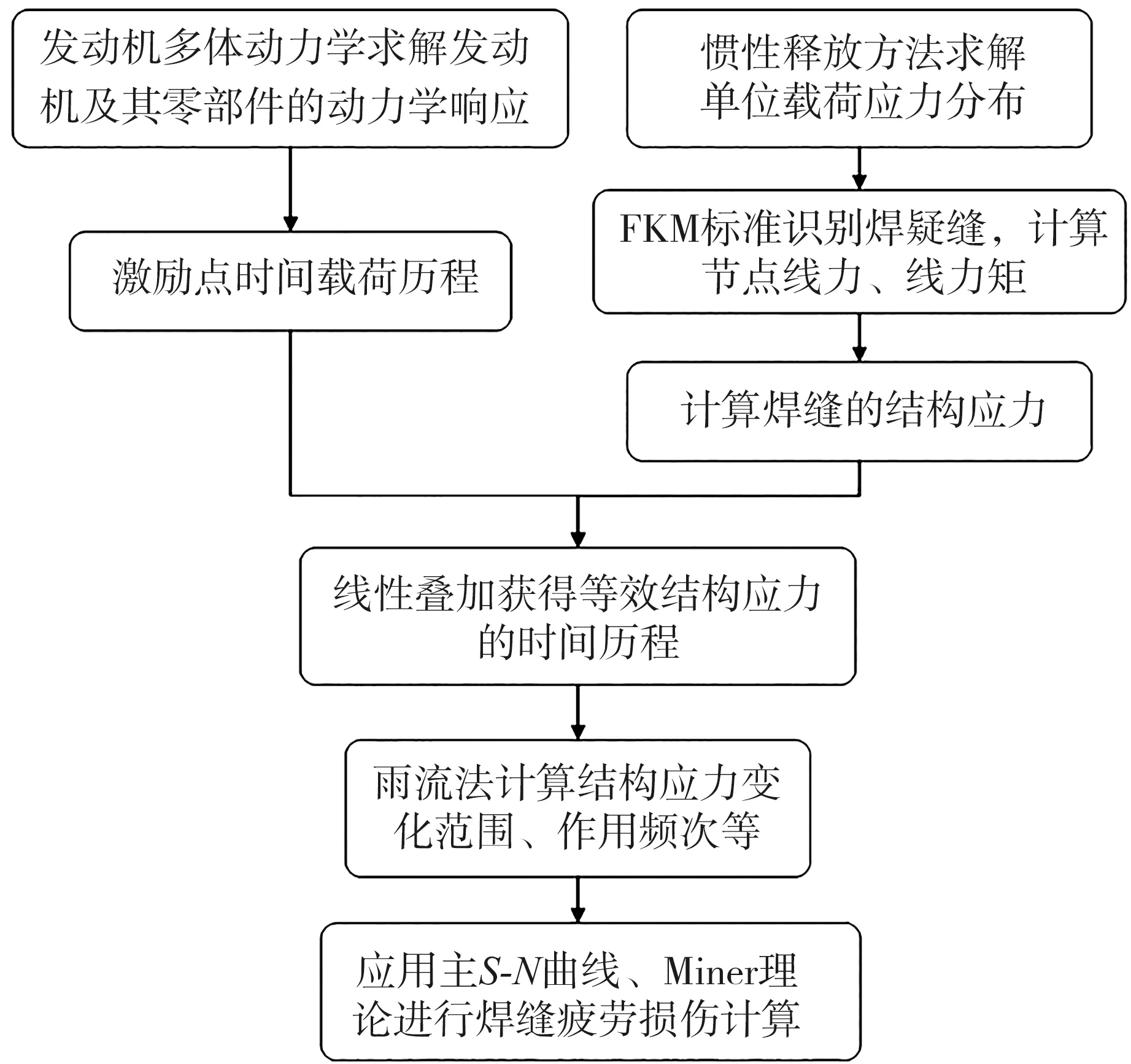
图6 准静态多通道法焊结构疲劳分析流程

4 消音器支架焊接疲劳分析

4.1 有限元模型

应用准静态多通道疲劳分析法对某发动机排气系统消音器焊接结构进行疲劳分析，消音器结构有限元模型及5个激励点布置如图7所示。消音器支架为焊接结构，材料为Q235A，厚度为8 mm，为单边T型焊接，焊趾高4 mm；消音器质量约为6.5 kg。

图7 消音器结构的有限元模型

消音器支架的焊缝单元采用四边形单元，单元尺寸取d/2。消音器体与消音器支架简化为绑定约束，消音器支架的螺栓孔、消音器法兰口建立刚性耦合单元RBE2，作为施加单位载荷的激励点；消音器体内部的筋板简化为多组刚性耦单元RBE2，采用质量单元COMN2模拟消音器的质量分布。有限元模型参数如表1所示。

表1 有限元模型参数

4.2 单位激励载荷作业下的应力分布

应用Optistruct求解器，求解在单位激励载荷作用下消音器支架的应力分布。在5个激励点位置施加3个方向的单位力载荷，共计15个激励载荷，即15个通道。在求解器中调用INREL卡片，采用自动惯性释放法，系统自动施加虚拟约束。激励点1在x方向的单位激励载荷应力分布如图8所示。

图8 激励点1单位载荷作用下的应力分布

4.3 激励点的载荷时间历程

采用发动机多体动力学计算激励点的载荷-时间历程。该方法主要基于牛顿动量守恒和欧拉角动量守恒原理，计算在燃烧爆压作用下的发动机及其零部件的动力学响应，评估发动机系统的振动和噪声性能。本文中搭建该型发动机的多体动力学模型，提取激励点的载荷时间历程，作为疲劳分析的动力学载荷输入。

发动机曲轴一个工作循环内，激励点1的载荷随曲轴转角的时间历程曲线如图9所示。

图9 一个工作循环内载荷时间历程曲线

4.4 疲劳损伤预测

焊接结构的失效以焊根或焊趾位置的疲劳破坏为主。本文中应用FKM标准定义焊缝的厚度为4 mm，坡角为45°，熔深率为0.3。考虑疲劳数据的离散性，在存活率为95%(2倍标准差)情况下，主S-N曲线中的试验常数Cd、h分别为9915、-0.312 8，输入单位激励载荷作业下的应力分布和激励点的载荷时间历程，计算得到发动机一个工作循环内的消音器支架的疲劳损伤分布如10图所示。

由图10可知，最大损伤位于焊缝焊趾顶面的节点87 525(焊缝起始位置)处，缺口系数为5.672，最大损伤为3.95×10-9。

图10 一个工作循环内消音器支架的疲劳损伤分布

该机型发动机的额定转速为2400 r/min，工作时间为500 h，曲轴转过7.2×107r，曲轴转2 r为一个工作循环，循环载荷作用次数为3.6×107次，因此焊缝节点87 525的实际最大损伤为0.142，低于损伤断裂临界值1.000，表明位置的疲劳损伤满足要求。

该焊接疲劳评估方法在市场验证和跟踪中表现良好，经该方法评估过的发动机因疲劳损伤导致的故障率很低，该方法具有较高的准确性和良好的应用价值。

5 结语

本文中引入FKM标准，以结构应力法为基础，应用焊根和焊趾的缺口系数，计算焊接接头的缺口应力，结合主S-N曲线，实现载荷输入、应力求解、焊缝识别和疲劳分析与评估的一体化作业，可在产品设计初期对焊接结构的寿命进行预测，具有较高的工程应用价值；而且应用灵活、高效，可用于不同领域的各类焊接结构的疲劳和分析。

发动机多体动力学和准静态多通道疲劳损伤法，是对实际振动载荷的简化，需要不断积累测试数据或者通过疲劳试验方法，不断优化载荷，以减少误差。