基于蒙特卡洛法的发动机压缩余隙尺寸链计算

刘泽涛，徐庆增，徐玺涛

潍柴动力股份有限公司, 山东潍坊 261061

0 引言

柴油发动机压缩行程中，最大行程容积与最小容积之比为压缩比[1-2]，大部分柴油发动机的压缩比为15～22[3]。压缩比越大，燃烧压力和功率越大，燃烧温度越高，燃油经济性越好。压缩比应控制在一定范围内，压缩比过大可导致发动机出现爆燃，过小则会导致动力不足、燃油消耗高等现象，维持压缩比处于正常范围非常重要[4]。压缩余隙为活塞处于上止点时，活塞顶面与气缸盖底面之间的距离，是压缩比最直观的体现。对于定型的发动机，压缩比应为定值，但由于加工、装配、工作时间、工况、修理方法的差异，导致相同机型出现不同的压缩比。传统压缩余隙计算为设计工程师利用极值法手算，或者尺寸工程师利用公差分析软件进行计算，但前者无法保证计算精度，而后者计算过程耗时较长。本文中采用蒙特卡洛法，构建压缩余隙的尺寸链，设计计算程序，计算压缩余隙，与VSA仿真数据进行对比，验证其准确性及易用性，再通过试验数据进行复核，确保该计算方法可行、精确。

1 公差分析理论基础

公差分析是指分析产品内部零部件之间的尺寸关系，查找满足这些设计指标的影响因子尺寸，根据这些尺寸参数并按照一定的计算方法和置信水平，计算出尺寸链封闭环的变动范围[5]。

1.1 尺寸链

尺寸链是公差设计、分析的基础，发动机常规设计(包括生产工艺)中，活塞压缩高度、曲轴回转半径等设计都是通过严格的尺寸链计算。以产品装配为例，尺寸链由多个零件相关特征装配而成，其对应的特征尺寸相互连接构成的闭环回路，如图1所示。图1中，已知的特征尺寸A0、A1、A2定义为尺寸链的组成环，未知的尺寸A3则定义为封闭环，封闭环和组成环共同构成尺寸链[6]。公差设计是否合理取决于尺寸链的分析精确度[7]。目前，尺寸链的计算方法主要有极值法和统计法。

图1 尺寸链示意图

采用极值法计算尺寸链，需要组成环的每个尺寸都处于其上、下偏差之间[8]，此时对封闭环尺寸要求最严格。极值法计算尺寸链，装配零件不需要考虑尺寸因素，可以百分百达到零件的互换，但是加严了尺寸链的计算公差，提升了成本。极值法主要应用于尺寸链组成环较少、零件尺寸要求互换的情况。

统计公差计算方法[9]主要有概率法、蒙特卡洛模拟法等，多用于大批量生产、尺寸链环数多等情况。概率法是一种以概率论为基础，在一定置信水平下计算尺寸链封闭环的方法，其中的组成环和封闭环尺寸为相互独立的、满足一定概率分布的变量；概率法不要求装配零件能够完全互换。与概率法类似，蒙特卡洛模拟法采用零件特征尺寸的概率分布代替尺寸计算，不同的是其利用随机抽样取数算法，随机生成组成环装配序列，从而模拟实际装配。

1.2 蒙特卡洛法尺寸链的实现

采用蒙特卡洛法进行尺寸链计算时，需要采用某种概率分布对每个组成环尺寸随机抽样，然后根据抽样结果随机装配[10-12]，在一定情况下，可以得到较符合实际生产的结果。蒙特卡洛法尺寸链的计算步骤为：1)确定组成环尺寸的概率分布规律；2)根据所要达到的精度(99.73%、99.993 7%等)随机抽样，确定每个组成环尺寸的随机数；3)将多个组成环进行相关计算(尺寸链方程)即可得到封闭环尺寸的m个随机样本数据；4)对封闭环尺寸随机样本数据进行相关数理统计处理，得到平均值、方差、公差等。

1.2.1 组成环尺寸随机模拟实现

根据文献[13]，对于连续随机变量，均匀分布是其他概率分布的基础，通过变换可以将均匀分布转换为任意的概率分布。对组成环的尺寸进行随机取数时，可以先在(0,1)内进行均匀取值，然后根据对应公式进行转换。其中，(0,1)内的随机数通过程序C语言中的Random()函数生成。

根据大数据分析，产品零件的生产规律一般符合正态分布。若R1、R2为2个相互独立的符合均匀分布的随机数，则符合标准正态分布N(0,1)的随机数

正态分布N(μ，σ2)下的随机数y可以由标准正态分布随机数得到：

1.2.2 封闭环尺寸数理统计实现

经过上一步计算模拟，得到尺寸链封闭环的m个(x1，x2，…，xm)正态分布样本数据，对其进行相关数理统计计算，求解封闭环尺寸的均值、极值、公差等。

封闭环尺寸样本均值

样本极大值

xmax=max(x1,x2,…，xm),

样本极小值

xmin=min(x1,x2，…,xm)。

封闭环尺寸的上偏差ES和下偏差EI分别为：

2 压缩余隙数学模型

2.1 装配关系分析

压缩余隙三维模型如图2所示，各零部件间具有以下装配关系。

1)机体为主装配零件，几乎所有的运动件、外围件等都会安装在机体上。

2)曲轴通过主轴颈与机体主轴承孔(需安装主轴瓦，防止曲轴与机体直接接触)的孔轴配合安装在机体上，为间隙配合，保证曲轴能够在机体内旋转。

3)连杆大头(需安装连杆轴瓦，防止连杆与曲轴直接接触)与曲轴的连杆轴径为间隙配合，小头(需安装连杆衬套，防止连杆与活塞销直接接触)与活塞销为间隙配合。

4)气缸套台阶面与机体气缸套安装面装配，起到限位作用，部分发动机没有气缸套。

5)连杆小头与活塞销为间隙配合装配，连杆小头与活塞多为过度配合，活塞通过活塞环等保证与气缸套内孔的孔轴配合。

6)气缸盖通过气缸盖垫片安装在机体顶面。

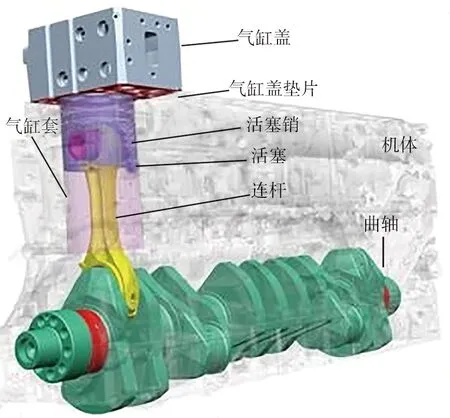
图2 压缩余隙三维模型

2.2 尺寸链模型构建

热态和冷态下的压缩余隙不同。冷态指正常生产装配情况，热态指发动机运行稳定工况下的状态。为便于设计的快速计算，通常只计算冷态下的压缩余隙；若计算热态压缩余隙，只需进一步考虑热态膨胀量即可。

a)轴在下 b)轴在上 图3 重力作用下孔轴配合模型

计算冷态压缩余隙时需要考虑重力的影响，为快速计算，将各孔轴配合中重力作用简化为图3所示，孔轴配合的接触点、孔径、轴径可以作为尺寸链组成环转换点。构建尺寸链的第一步是明确封闭环，本文中封闭环是压缩余隙。构建尺寸链可从封闭环两侧对应的特征入手，也可从主装配件——机体入手。原则上，尺寸链的建立与图纸标注有关，标注样式不同、标注特征起点位置的变化都会影响尺寸链结果。尺寸链的构建过程包括如下11个步骤。

1)从活塞顶面入手，第1环为活塞压缩高，即活塞顶面与活塞销孔的距离。

2)第2环为活塞上活塞销孔与活塞销的配合，根据图3中模型建立相关尺寸链，涉及的特征尺寸为活塞销孔直径、活塞销轴径。

3)第3环为活塞销与连杆小头的配合，根据图3中模型建立相关尺寸链，涉及特征为活塞销轴径、连杆小头孔径(带衬套)。

4)第4环为连杆大、小头间距。

5)第5环为连杆大头与曲轴连杆轴颈的配合，根据图3中模型建立相关尺寸链，涉及特征尺寸为连杆大头孔径(带瓦)、曲轴连杆轴颈直径。

6)第6环为曲轴连杆轴径与曲轴主轴颈的距离，即回转半径。

7)第7环为曲轴主轴颈与机体主轴承孔的配合，根据图3中模型建立相关尺寸链，涉及特征尺寸为机体主轴承孔孔径(带瓦)、曲轴连杆轴颈直径。

8)第8环为机体主轴承孔与机体顶面的距离。

9)第9环为机体顶面与安装气缸套面的距离，如果发动机没有气缸套，则不存在此环。

10)第10环为气缸套台阶面高度，如果发动机没有气缸套，则不存在此环。

11)第11环为气缸盖垫片压缩后的厚度。

构建的尺寸链如图4所示，其中箭头的方向只是用于判断尺寸链增减环。

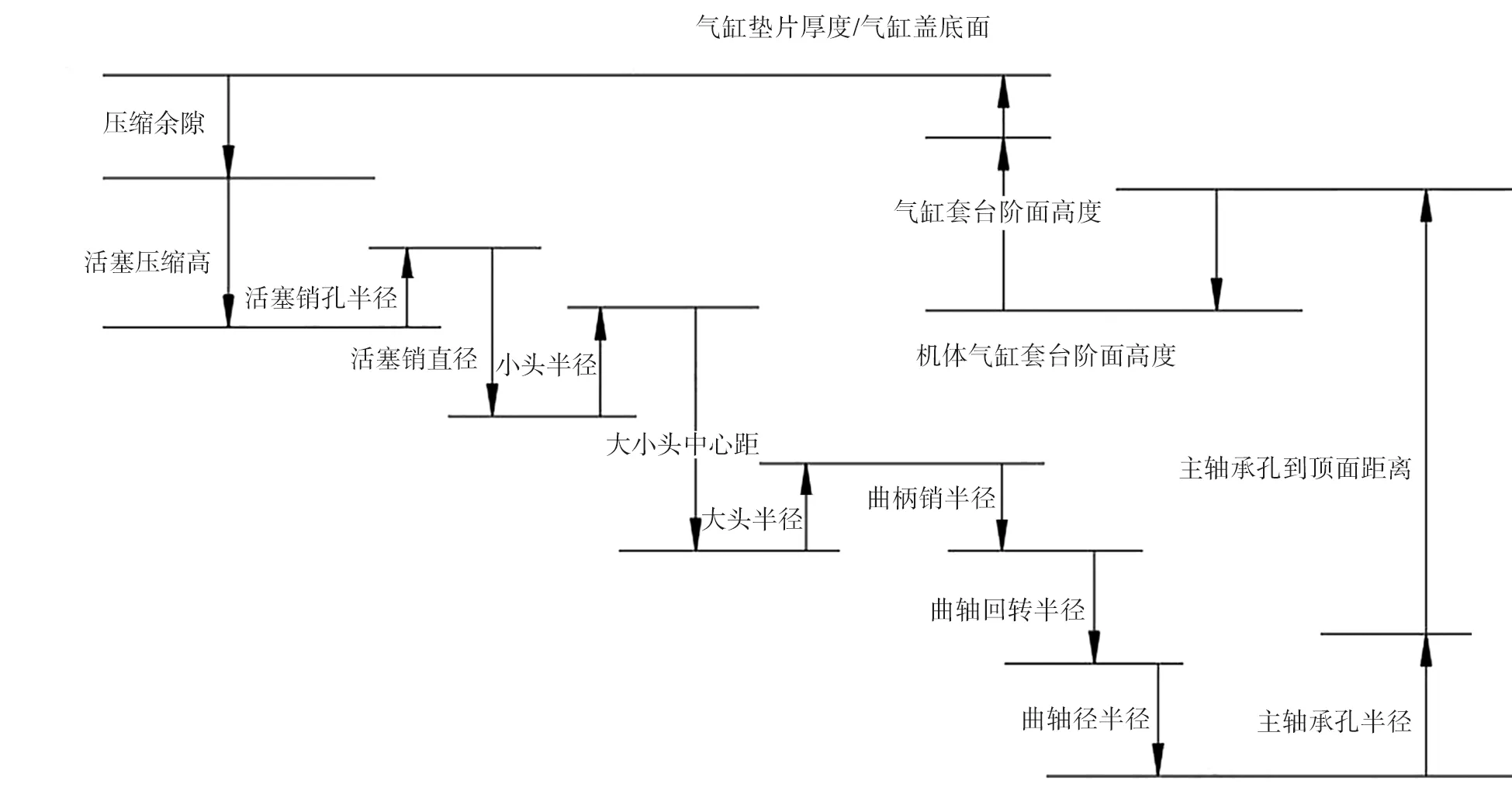
图4 压缩余隙尺寸链模型

3 仿真与试验验证

以某发动机为例构建压缩余隙尺寸链模型，假设尺寸链组成环的尺寸均按正态分布，加工水平为3σ，标准差则为尺寸公差的1/6，每个组成环随机取数并计算其取值标准差，结果如表1所示。

表1 压缩余隙尺寸链蒙特卡洛法标准差

自主设计压缩余隙计算程序，程序流程图如图5所示。输入表1数据，运行程序，得到压缩余隙计算结果为(0.841 1±0.090 5)mm，即0.750 6～0.931 6 mm。采用仿真软件VSA计算压缩余隙，结果如图6所示。根据样本得出压缩余隙为0.728 5～0.961 2 mm，根据样本推算整体，压缩余隙为0.755 7～0.936 7 mm。对比2组数据，自主设计程序与VSA仿真软件的压缩余隙计算结果基本相同。

图5 自研程序流程图

图6 压缩余隙仿真计算结果结果

实际测量328台试验发动机的压缩余隙。每台机器的所有组成环特征尺寸均按照中值加工装配，测量冷态下发动机压缩余隙，结果如图7所示。由图7可知，最大压缩余隙约为0.949 9 mm，最小压缩余隙约为 0.732 1 mm。考虑到部分零件加工难度较大，可以认为，自研程序及VSA仿真的压缩余隙计算结果均与实际装配结果相符。

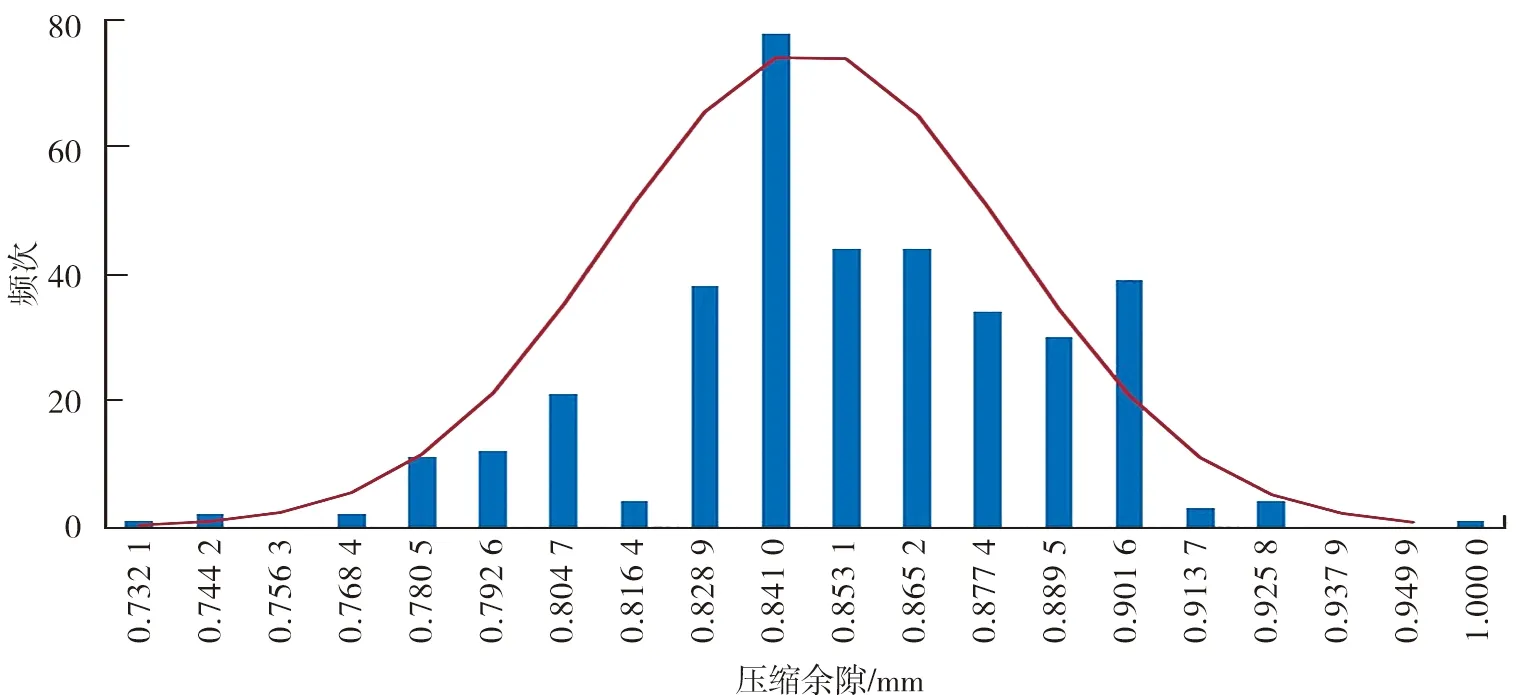
图7 冷态下压缩余隙测试结果

相对于VSA仿真程序，自主设计程序计算速度快，无需建立繁琐的VSA三维模型，且无需输入全部公差。本文中的尺寸链及压缩余隙的计算方法可应用于快速计算发动机压缩余隙。

4 结论

1)构建基于尺寸链计算原理和蒙特卡洛法的尺寸链计算方法，开发尺寸链计算程序，并与VSA仿真结果、实际试验数据相对比，验证了建立的尺寸链模型及自研程序计算压缩余隙的准确性。

2)采用该方法可快速计算发动机冷态下的压缩余隙，提高计算精度，缩短研发周期，克服了极值法精度不高的缺点，可作为同类一维尺寸链计算的参考。