钝感双基发射药迁移失效评价方法
梁昊 ,丁亚军 ,李世影 ,赵先正 ,肖忠良
(1.南京理工大学 化工学院,江苏 南京 210094;2.南京理工大学 特种能源材料教育部重点实验室,江苏 南京 210094)
0 引言
发射药是枪炮类身管武器的能源材料,对武器的综合性能和作战效能有着至关重要的影响[1]。
钝感双基球扁发射药广泛使用于国内外中小口径枪械武器,通过在发射药基体中渗入邻苯二甲酸二丁酯(DBP)、樟脑等阻燃分子,可以达到降低发射药起始燃烧猛度、降低膛压、提高燃烧渐增性和弹丸初速的目的[2]。
发射药等含能材料通常具有热分解产物自催化现象,加入化学安定剂能够与其热分解产物反应,从而抑制热分解自催化过程,进而达到发射药长期安定贮存的目的。既往关于发射药老化现象的研究以及老化评价方法都限于化学变化层面,主要通过化学安定剂含量的减少来评定[3-5]。
近些年出现了钝感双基发射药在老化一定时间后射击超压严重的现象,而测定其安定剂含量结果远未失效。由此可见,对于非均质钝感发射药而言,仅从化学变化角度考量发射药老化问题是不完全的,要同时兼顾其物理变化过程[6-7]。
钝感双基发射药存在上述问题的根源在于发射药体系中增塑剂或者钝感剂的迁移现象,如硝化甘油(NG)、太根、二硝基甲苯(DNT)、DBP 等,是通过扩散作用在温度和钝感剂浓度差等驱动下的时间积累[8]。钝感剂迁移失效会导致发射药的燃烧渐增性下降、膛压升高,对发射装药的使用安全性带来严重危害。综合考虑发射药老化过程中的化学变化和物理变化,钝感双基发射药的老化过程如图1 所示。

图1 钝感双基发射药的老化过程Fig.1 Aging process of deterred double-base propellant
目前尚未有基于物理变化层面对钝感双基发射药迁移失效的评价方法。因此,迫切需要开展钝感发射药迁移失效评价研究,为今后老化钝感发射药的使用安全性评价提供理论和数据支撑。
表征发射药的使用安全性最直接的方法就是射击实验,通过老化前后发射装药的最大膛压来判断。但是钝感剂迁移程度较高的老化发射药直接进行射击实验,很可能导致膛压过高,甚至出现膛炸、枪击损坏、底火脱落等重大危害。密闭爆发器是一种具有超高耐压特性、常用以测试发射药静态燃烧性能的装置,可重复性好,安全可靠,已在各个国家含能材料的研究中得到广泛应用[9-11]。因此以钝感发射药相同装填密度的老化发射药样品进行密闭爆发器实验,也是安全可靠的。
本文建立的钝感双基发射药迁移失效评价方法,基于密闭爆发器实验,通过发射药燃烧动态活度最大值升高幅度随老化时间的变化分析钝感双基发射药迁移失效的规律性,并用以评价所测老化发射药样品的使用安全性。
1 基本原理
1.1 钝感剂扩散规律
钝感剂-发射药体系的扩散行为属于典型的扩散剂-聚合物扩散体系。聚合物中的扩散现象极其复杂,扩散率介于液体和固体之间,取决于高分子内部结构、溶胀程度以及扩散剂-聚合物本身的相互作用等多种因素。
发射药的玻璃化温度一般高于其本身燃点,通常发射药的使用和贮存温度远低于玻璃化转变温度。在此情况下,发射药基体中聚合物的高分子网状结构紧缩、不能充分运动,扩散行为复杂。Trewartha 等[12]用共焦拉曼光谱研究了DNT 钝感的小口径武器发射药扩散谱图,由研究谱图分析得出该发射药的扩散分布均符合菲克第二扩散定律,也就是非稳态扩散。
非稳态扩散是指扩散物质在扩散介质中的浓度分布随时间发生变化的扩散,其扩散通量随位置与时间变化。菲克第二扩散定律的一维扩散式为

式中:C为扩散物质浓度(mol·m-3);x表示位置(m);td为扩散时间(s);D为扩散系数(m2/s)。
典型非稳态扩散的边界条件可分为两种情况:第1 种情况是在整个扩散中扩散物质在介质表面的浓度保持不变;第2 种情况是一定量的扩散物质由介质表面向内部扩散。
显然,对于钝感发射药而言,起初钝感剂分布在发射药颗粒表面,之后逐渐向内扩散,符合非稳态扩散的第2 种情况,可采用正态分布N(μ,σ)(其中μ为数学期望,σ为标准差)的右支描述。对于钝感发射药而言,μ=0;以3σ半置信区间作为钝感剂分布的深度d(m);保证分布函数积分为钝感剂总含量m(g),则钝感剂分布方程为
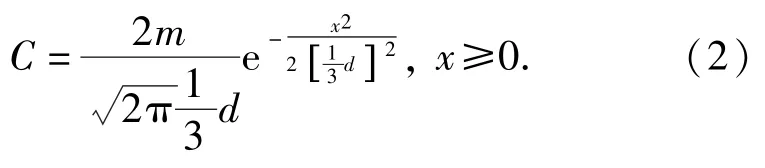
根据菲克第二定律的重要推论:扩散时间td与扩散距离d的平方呈正比,则

式中:k为相关系数;di和tdi分别为初始时刻的分布深度和等效扩散时间。
将扩散距离d与扩散时间td的关系代入钝感剂分布函数,则钝感剂分布方程为
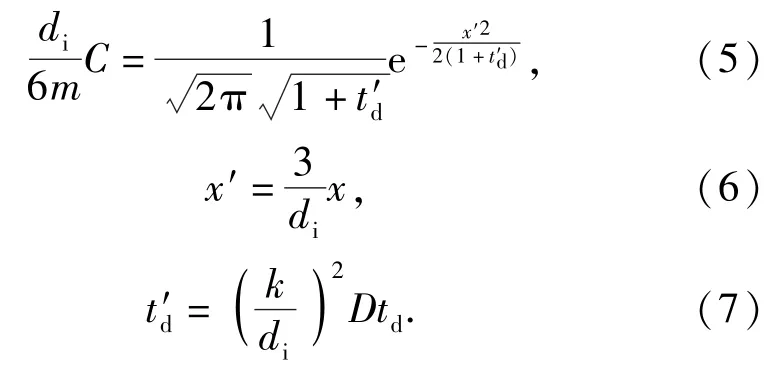
由此可见,钝感发射药老化过程中,钝感剂逐渐由表面向内迁移,导致钝感剂梯度分布性质减弱,发射药表面钝感剂浓度降低,从而导致发射药起始阶段燃烧动态活度升高,燃烧渐增性变差。
一般中小口径枪弹用发射药尺寸小,钝感剂分布在很小的尺度范围,测试误差很大。同时,发射药具有大样本特征,个别样品的钝感剂分布不能代表整体结果。对武器燃烧和内弹道性能的影响是一个统计平均的结果,因此可以采用燃烧性能间接表征与评价钝感发射药的迁移失效。
1.2 燃速系数与钝感剂浓度的关系
为探究发射药燃速系数与钝感剂浓度的关系,以90%硝化棉(NC)和10%NG 为基础,外加不同含量DBP 制成均质发射药进行密闭爆发器实验,燃速r(cm·s-1)与燃烧压力p(MPa)的关系如图2 所示,拟合得到燃速系数u1及线性拟合决定系数R2如表1所示(燃速压力指数n近似为1)。
由图2 和表1 可以看出:不同钝感剂含量发射药的r-p曲线均较好地符合线性关系;钝感剂的加入能够降低发射药整体的能量,致使发射药燃速系数降低。将DBP 外加含量转换成浓度,发射药燃速系数与钝感剂DBP 浓度的关系如图3 所示。

图2 不同外加DBP 含量发射药样品的燃速曲线Fig.2 Burning rate curves of propellants with different DBP extra contents

表1 不同外加DBP 含量发射药样品的燃速系数Tab.1 Burning rate coefficients of propellants with different DBP extra contents

图3 均质发射药燃速系数随DBP 浓度的变化Fig.3 Burning rate coefficients of homogeneous propellants with different DBP content ration
由图3 可见:在实验钝感剂浓度范围内,发射药的燃速系数随钝感剂浓度呈现出较好的线性下降趋势;钝感剂的加入降低了发射药的能量,从而使发射药的燃速系数及不同时刻的燃速降低,进而影响燃气生成猛度。
1.3 钝感剂浓度分布对燃气生成猛度的影响
由发射药的形状函数计算方法可知:

式中:Z为已燃相对厚度;e为已燃厚度(mm);e1为1/2 起始弧厚(mm);ψ为发射药已燃质量百分比;χ、λ、μ为与发射药药型相关的特性参数。
燃气生成猛度Γ可表示为

式中:t为燃烧时间(ms)。
综合(10)式~(12)式,Γ可转化为

从(13)式可以看出,当药型尺寸一定时,发射药的燃速系数是影响发射药燃气生成猛度的一个重要因素。
对于钝感发射药而言,初始状态发射药表面的钝感剂浓度最高,向内逐渐降低。在温度和浓度差驱动下,钝感剂通过扩散作用向发射药内部迁移,钝感剂浓度梯度逐渐减弱,最终在发射药基体内分布均匀。
钝感剂浓度梯度分布性质减弱导致的直接问题就是发射药表面钝感剂浓度下降,使得初始燃烧阶段发射药燃速变快,燃气生成猛度升高。同样体现在装药内弹道性质上,钝感剂的迁移导致发射药初始燃烧加快,在初始弹丸行程小、弹后空间不足的情况下使得膛内压力升高,出现弹道漂移现象,影响武器作战安全。
由此,通过发射药燃气生成猛度变化(实验中采用密闭爆发器实验的动态活度变化)来评价钝感发射药的迁移程度,从理论上是可行的,同时能够避免直接进行射击实验可能出现的危险。
闻喜县第一次全国水利普查包括河湖基本情况普查、水利工程基本情况普查、经济社会用水情况调查、河湖开发治理保护情况普查、水土保持情况普查、水利行业能力建设情况普查以及灌区和地下水取水井专项普查。各项普查数据获取、填表和审核工作由闻喜县水务局各相关股室负责,局长与股长签订了水利普查目标责任书。制定《闻喜县第一次全国水利普查工作制度》和《闻喜县第一次全国水利普查数据获取工作方案》,层层分解落实水利普查工作责任到各专业股室、各水利水保中心站和每一个普查工作人员。
1.4 钝感双基发射药迁移失效评价方法
采用密闭爆发器分别对发射药老化样品和未老化样品进行测试。实验温度为20 ℃;密闭爆发器容积规格为50 mL;装填密度为0.2 g/mL,装药量以实际标定爆发器容积乘以装填密度来计算;点火药为C 型NC,药量为0.55 g。
具体测试程序见国家军用标准GJB 770B—2005 火药实验方法703.1 密闭爆发器实验微分压力法。
密闭爆发器实验中通过压力传感器获取到发射药燃烧过程中的压力p随燃烧时间t的关系,再通过(14)式和(15)式转化得到发射药燃烧的动态活度值L和相对压力B:
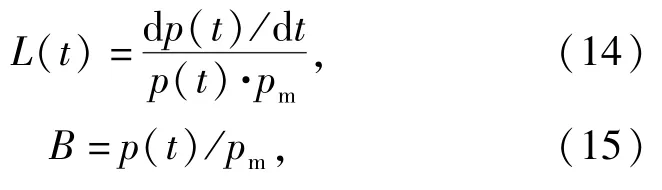
式中:pm为燃烧最大压力(MPa);tm为燃烧时间(ms)。
进一步通过(16)式得到动态活度最大值:

每份试样至少测定两次,以两个Lm差值不超过3%作为可信依据,取2 次有效结果的平均值作为实验测试结果,实验结果应表示至两位小数。通常中小口径用钝感发射药无孔或孔数较少,很少出现19 孔及以上药型发射药及其包覆发射药燃烧初始阶段动态活度值跳跃很大的情况。此外密闭爆发器实验中也可能受传感器、点火条件等影响而出现上述现象。若出现,则补测试样,直至结果有效。
将老化td时间后发射药样品的Lm值记为Lm(td),未老化样品的Lm值记为Lm(0)。
按(17)式处理得到老化td时间后发射药动态活度最大值升高百分比,记RL(td)为:

2 评价方法实验验证
2.1 动态活度随老化时间的线性增长
为了研究钝感双基发射药老化样品动态活度最大值升高幅度随时间的变化规律,对4 个不同配方、不同钝感剂用量及不同加速老化温度的老化发射药样品进行密闭爆发器实验,具体条件如表2 所示。每组样品加速老化不同天数后的动态活度最大值升高百分比如图4 所示。表2 中,kd为迁移驱动因子。
由图4 可见,4 组老化样品的RL(td)-td曲线均较好符合线性增长规律,4 组样品RL(td)-td曲线的斜率即kd及拟合度如表2 所示。从表2 中可以看出,不同配方、不同钝感剂用量及不同加速老化温度T的老化发射药样品呈现出不同的增长速率,但均较好地符合线性增长规律,表明通过动态活度最大值升高幅度随老化时间的变化来评价发射药迁移程度的方法适用范围广。
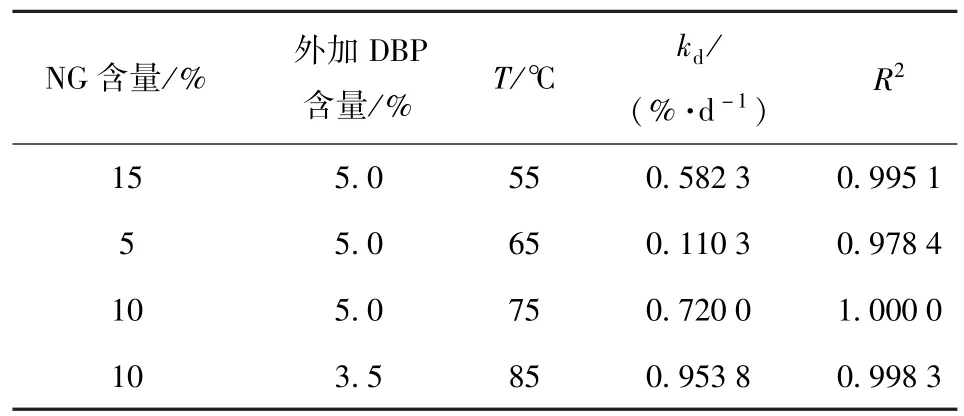
表2 RL(td) -td直线的斜率kd及拟合度Tab.2 Slope and degree of fitting of RL(td)-td lines
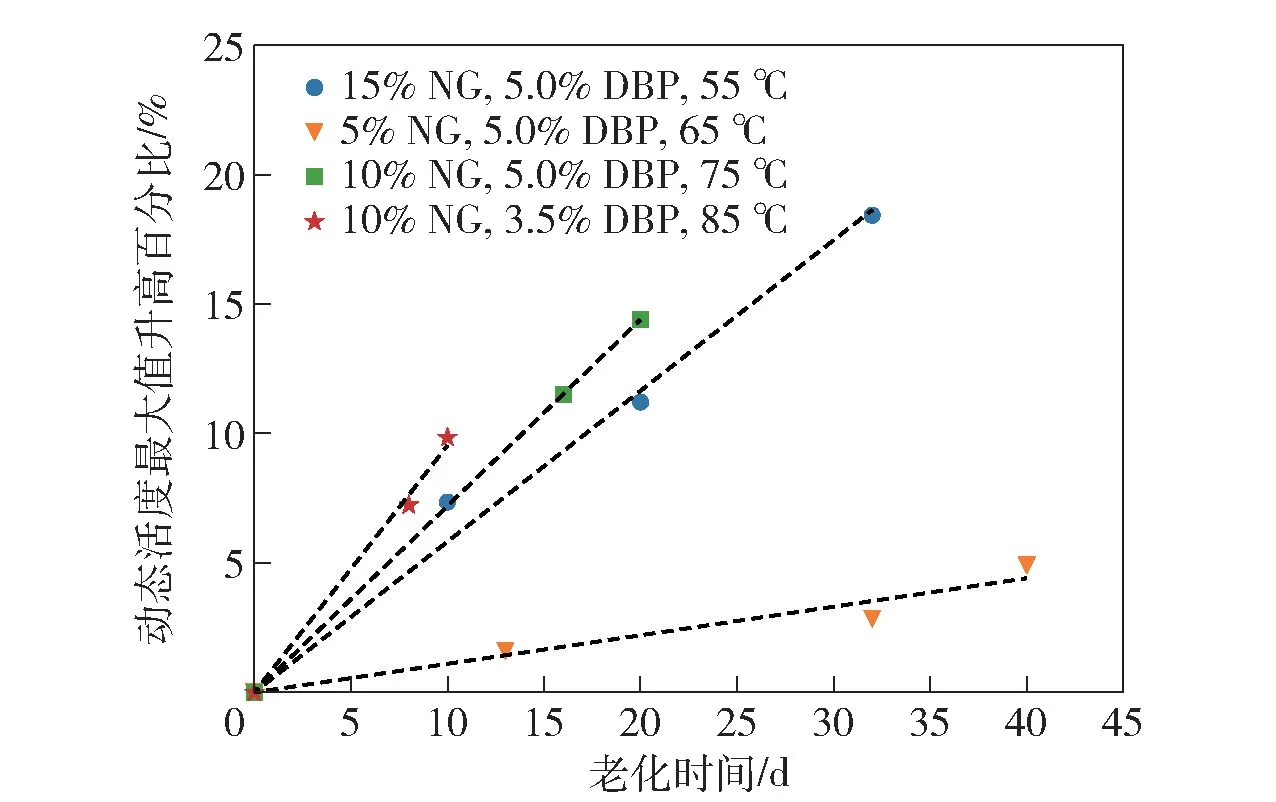
图4 动态活度最大值升高幅度随老化时间的线性增长规律Fig.4 Linear growth of the increasing percentage of maximum dynamic vivacity with aging time
2.2 动态活度最大值升高百分比阈值
为确定“使用安全性(动态活度最大值升高百分比)”阈值,采用水浴烘箱对同一发射药样品进行55 ℃加速老化处理,之后通过密闭爆发器及射击实验分析了动态活度最大值以及最大膛压升高幅度随老化时间变化的对应关系。发射药样品含10%NG(其他为NC 及安定剂),钝感过程采用发射药质量5%的DBP 进行液相钝感。
2.2.1 动态活度最大值升高幅度随老化时间变化规律
该发射药55 ℃老化12 d、28 d、40 d 及未老化样品的动态活度-相对压力曲线如图5 所示,相应的动态活度最大值Lm随老化天数变化规律如图6所示。
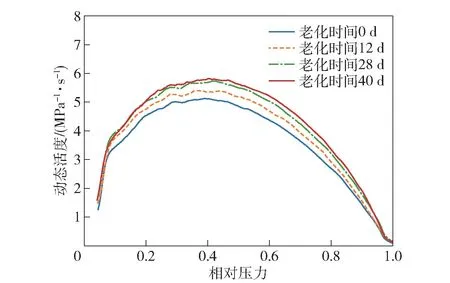
图5 老化样品动态活度-相对压力曲线随老化时间的变化关系Fig.5 Relationship between L-B curve and aging time

图6 老化样品动态活度升高幅度与老化时间的关系Fig.6 Relationship between the increasing percentage of dynamic vivacity and the aging time
该发射药的迁移过程仍较好地符合前述线性增长规律,其动态活度最大值升高幅度随老化时间的关系如(18)式:

2.2.2 最大膛压升高幅度随老化时间变化规律
采用某弹道枪进行射击实验,不同老化时间样品选取相同装药量1.75 g,采用铜柱测压法记录不同样品的最大膛压pb(MPa),结果如表3 所示。
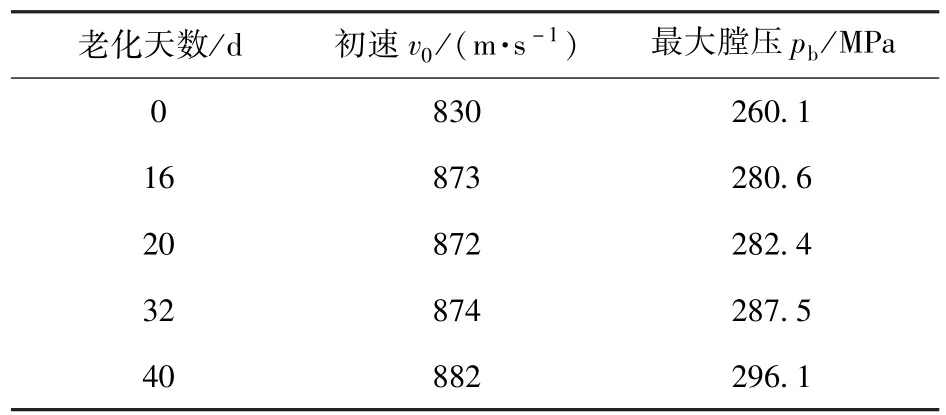
表3 不同老化时间样品的弹道实验结果Tab.3 Ballistic test results of samples with different aging time
记不同老化时间样品的最大膛压升高百分比Rp为

不同老化时间样品最大膛压升高幅度随老化时间的变化规律如图7 所示。
从图7 中可以看出,射击实验中该发射药最大膛压升高幅度随老化时间的变化关系也较好地符合线性增长规律,对应关系可表示为(20)式:
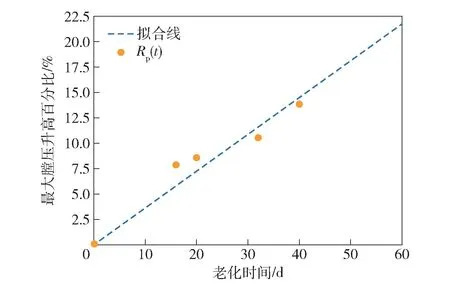
图7 最大膛压升高幅度与老化时间的关系Fig.7 Relationship between the increasing percentage of maximum chamber pressure and the aging time
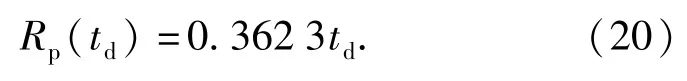
2.2.3 对应关系及失效阈值确定
基于钝感发射药老化迁移过程中RL(td)与Rp(td)随老化时间均呈线性增长趋势,可以得到相同老化时间下RL(td)与Rp(td)的关系,如(21)式:

将最大膛压升高百分比Rp(td)=10%的弹道迁移失效条件[13]代入RL(td)与Rp(td)关系式,可知RL(td)=8.64%。因此对于该品种发射药而言,其达到弹道迁移失效对应的动态活度最大值升高百分比阈值为8.64%,此后只需做该品种发射药老化样品的密闭爆发器实验,即可判定其是否迁移失效。
3 迁移失效与安定性失效对比
3.1 小分子钝感发射药
选取小分子DBP 钝感的发射药样品,分别在55 ℃、65 ℃和75 ℃下加速老化8 d,通过气相色谱和密闭爆发器对老化发射药样品进行安定剂含量及动态活度测试,结果分别如图8~图10 以及表4 所示。其中发射药样品中NG 含量为20% (其他为NC 及安定剂),钝感过程采用发射药质量5% 的DBP 进行液相钝感。
由图8、图9、图10 及表4 可以看出:该发射药样品75 ℃老化8 d 后,安定剂含量减少10.33%,远小于贮存失效阈值50%[14-15];从燃烧实验结果来看,钝感剂迁移导致发射药燃烧加快、燃烧时间变短、动态活度最大值升高,其中迁移程度最小的发射药样品RL(td)=14.83%,由于Rp(td)随老化时间的变化比RL(td)更为敏感,该样品射击潜在危险性很大,可以判定其已经迁移失效。
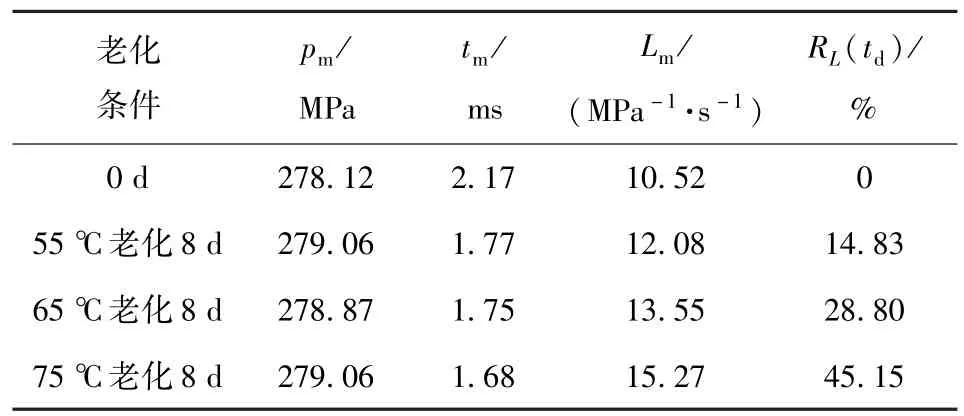
表4 DBP 钝感发射药老化样品的燃烧参数Tab.4 Burning parameters of aged DBP-deterred propellants
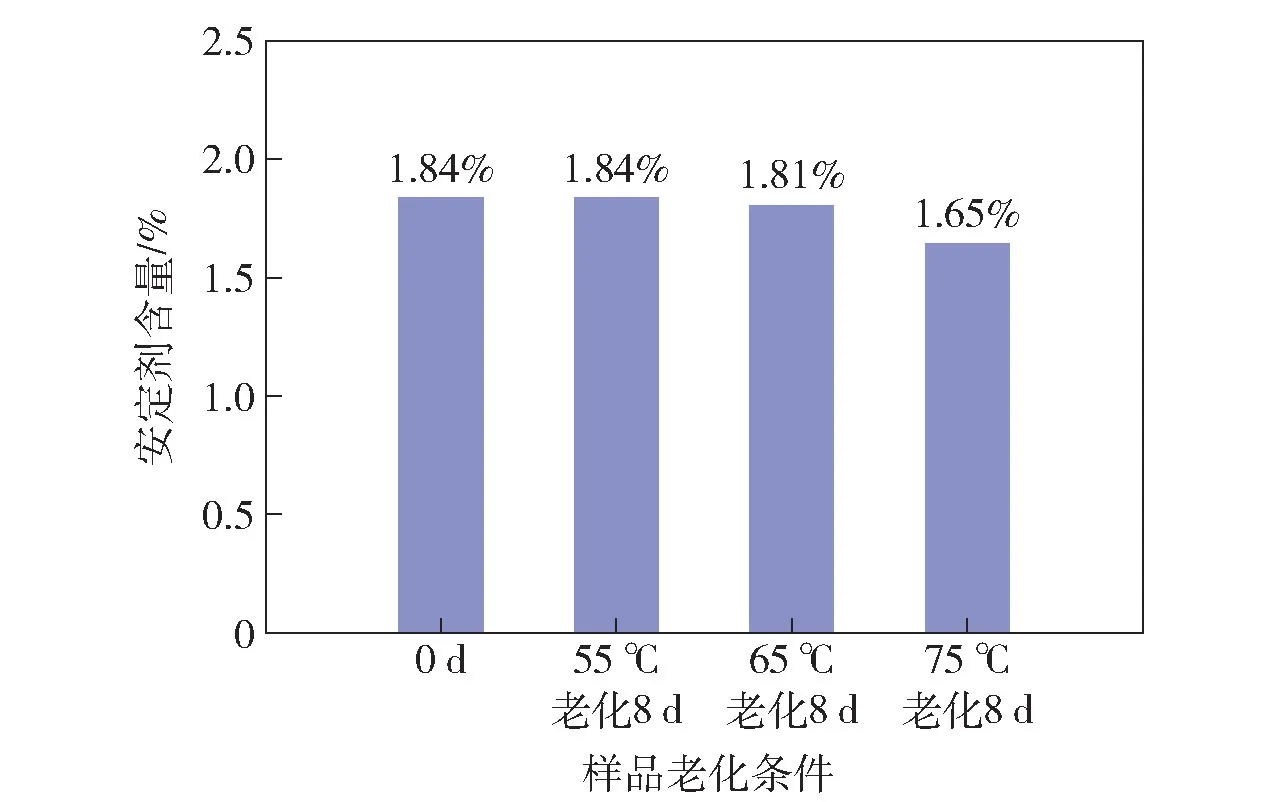
图8 DBP 钝感发射药老化样品安定剂含量Fig.8 Content of stabilizer in aged DBP-deterred propellants

图9 DBP 钝感发射药老化样品的燃烧压力-时间曲线Fig.9 p-t curves of aged DBP-deterred propellants
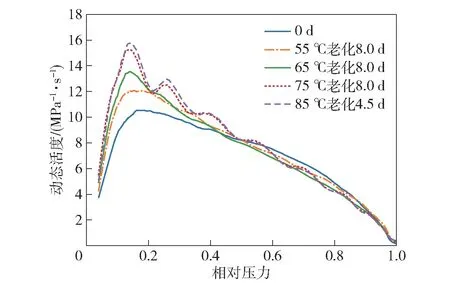
图10 DBP 钝感发射药老化样品的动态活度-相对压力曲线Fig.10 L-B curves of aged DBP-deterred propellants
3.2 高分子钝感发射药
聚酯钝感剂(NA)是一类由多元酸和多元醇缩聚反应得到的聚合物,选取NA 钝感的发射药样品分别在65 ℃和75 ℃下加速老化8 d,通过气相色谱和密闭爆发器对老化发射药样品进行了安定剂含量及动态活度测试,结果分别如图11~图13 以及表5所示,其中发射药样品中NG 含量为15%(其他为NC 及安定剂),钝感过程采用发射药质量5%的NA进行液相钝感。
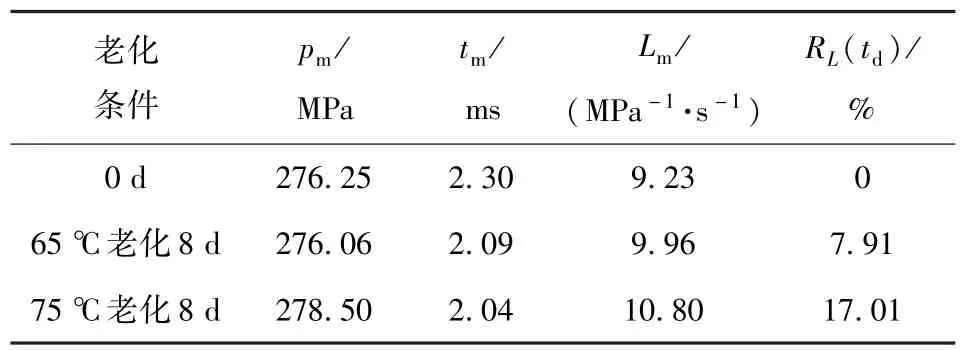
表5 NA 钝感发射药老化样品的燃烧参数Tab.5 Burning parameters of aged NA-deterred propellants
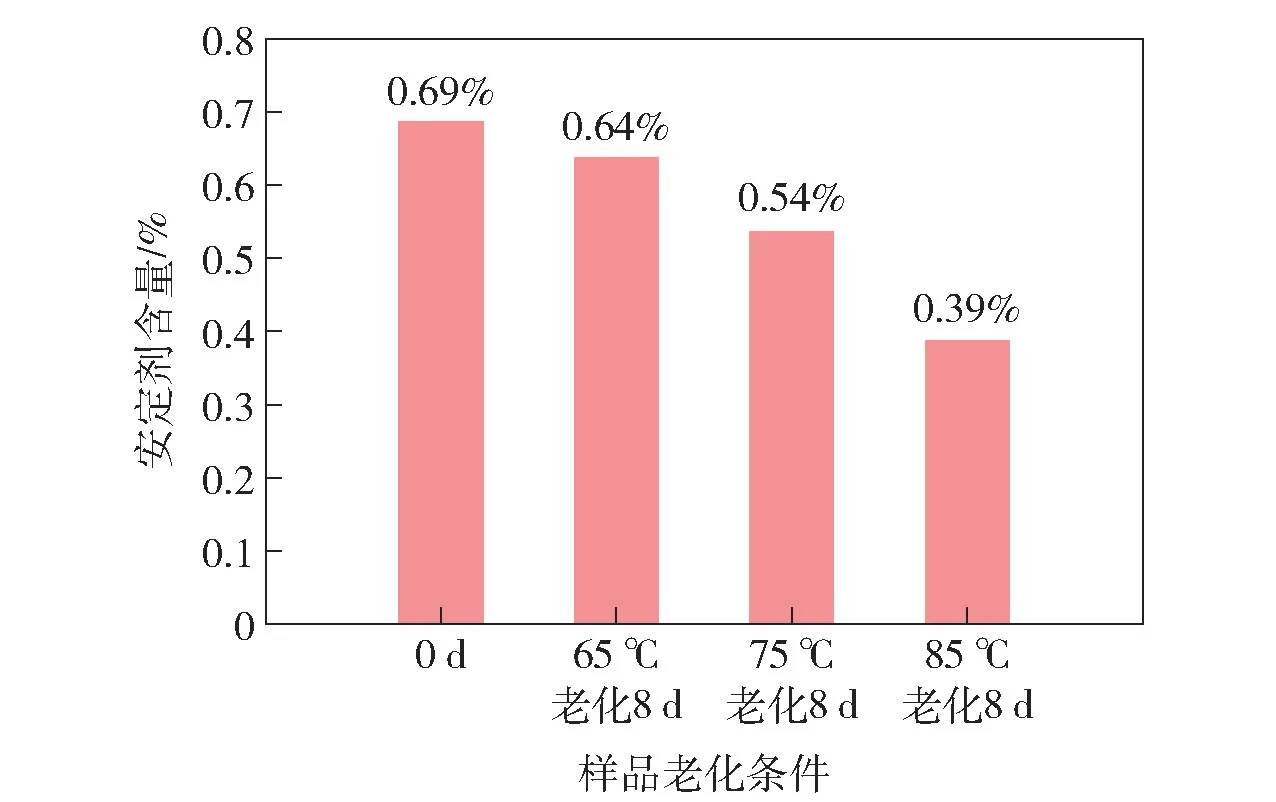
图11 NA 钝感发射药老化样品安定剂含量Fig.11 Content of stabilizer in aged NA-deterred propellants
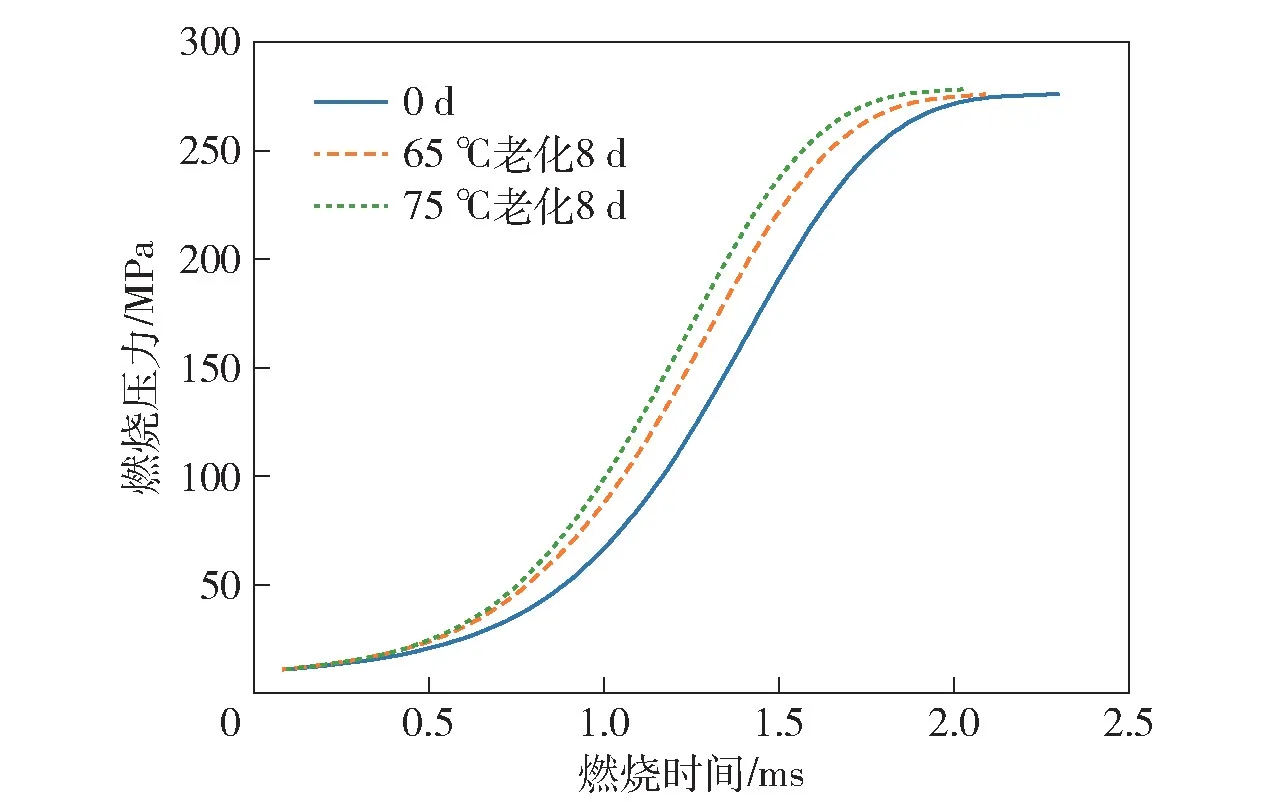
图12 NA 钝感发射药老化样品的p-t 曲线Fig.12 p-t curves of aged NA-deterred propellants

图13 NA 钝感发射药老化样品的动态活度-相对压力曲线Fig.13 L-B curves of aged NA-deterred propellants
从图11 可以看出,该发射药样品75 ℃老化8 d后,安定剂含量减少21.74%,远小于贮存失效阈值50%。但从燃烧结果来看,75 ℃老化8 d 后的发射药样品RL(td)=17.01%,因此该发射药样品已经迁移失效。
虽然相同条件下高分子钝感发射药老化迁移的程度要低于小分子钝感发射药,但无论是小分子还是高分子,作为钝感剂,都不可避免钝感剂在发射药基体中的迁移现象。而且在实验钝感剂用量范围内,发射药中钝感剂迁移失效的速率比发射药中安定剂的失效速率更快。
因此,对于老化钝感发射药,不仅要考量其安定剂含量变化、判断贮存安全性,还要测定老化迁移程度来判断其使用安全性。
3.3 钝感发射药老化性质综合评价
基于钝感双基发射药的钝感剂非均相分布特点,针对钝感双基发射药的老化性质考量,应遵循安定剂含量和动态活度最大值升高幅度的双阈值原则,具体判定步骤如图14 所示。
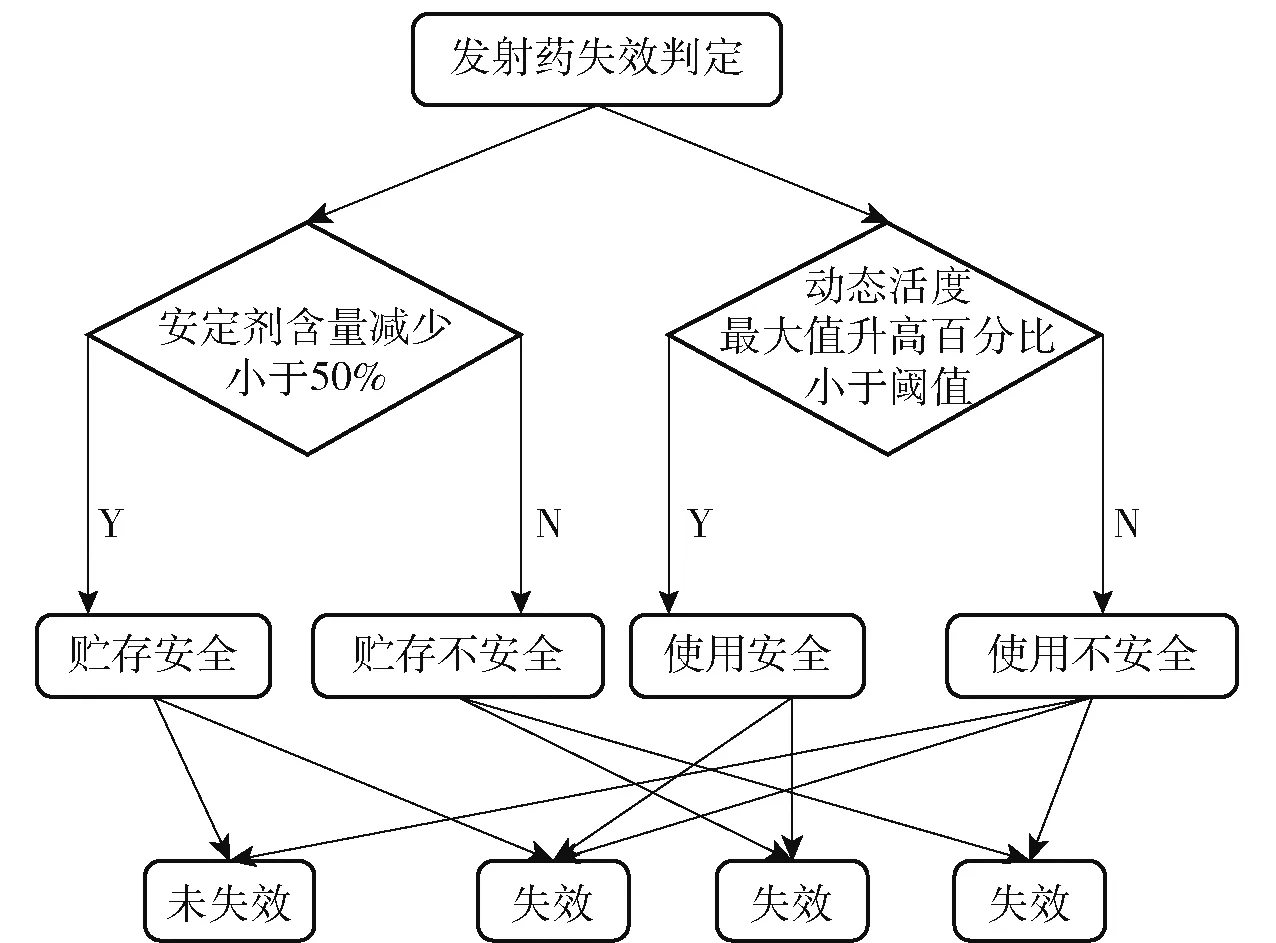
图14 钝感发射药老化失效双阈值判定步骤Fig.14 Double-threhold determination steps of invalidation
安定剂含量减少百分比和动态活度最大值升高百分比同时满足在阈值范围内,才可判定老化发射药试样未失效,继续贮存和使用较为安全;二者中任何一个先达到阈值,均判定为已失效。
4 结论
本文基于扩散原理、钝感剂分布与燃烧性能的关联,建立了钝感发射药迁移失效评价方法,并开展实验验证。所得主要结论如下。
1)通过将某一发射药动态活度最大值随老化时间升高规律和射击最大膛压升高规律相关联,可以得到该发射药动态活度最大值升高百分比阈值,从而有效判断该品种发射药老化样品的使用安全性。
2)气相色谱实验分析发射药中安定剂含量随老化时间的变化,对比燃烧规律,表明钝感发射药老化迁移导致的失效早于化学安定性失效。
3)钝感发射药老化失效应遵循双阈值原则,保证钝感发射药的贮存安全性和使用安全性。

