裸态平底榴弹底向下垂直跌落时弹丸和引信的冲击特性

金路轩,闻泉,王雨时,王光宇,张志彪

(南京理工大学 机械工程学院,江苏 南京 210094)

0 引言

对于弹药勤务处理的研究一直是国防领域至关重要的工作。从装配出厂到起爆战斗部为止,引信要经受许多环境。在装卸、搬动、运输和装填过程中,由于偶然跌落,引信、弹丸、定装式全弹或包装箱就会与地面或舰船甲板等目标发生碰撞,轻则影响弹药的使用性能,重则降低安全性甚至发生意外爆炸,造成人员伤亡。跌落高度和跌落目标对引信跌落安全性影响非常明显,为检验引信在勤务处理中的跌落安全性,国家军用标准GJB 573A—1998 引信环境与性能试验方法中规定了裸态全备引信或装有全备引信的弹丸以规定的高度向钢板和其他可信目标跌落的试验方法。

引信跌落所产生冲击作用力的波形、峰值和作用时间会随着弹丸和引信的质量、结构、材料、跌落高度、碰击姿态以及地面或其他跌落目标的性质等因素的不同而不同。跌落冲击是一种复杂的非线性瞬态响应过程,采用理论建模和数值分析的可能性不大,而传统跌落试验也存在着诸多问题:一是由于测试历程时间短,难以对试验过程中的特征进行提取,无法观察到引信内部特性;二是跌落姿态即碰撞角度难以控制,可重复性差,且难以出现完全垂直跌落的极端情况;三是试验准备周期长、费用高、数据测定困难。文献[5]以某型引信冗余保险系统为例,对其进行了不同落高、不同介质(水泥、沥青、土壤和钢板)的45°倾斜跌落试验,并在此基础上建立了冗余保险系统动力学模型进行数值仿真,其研究结果表明:该机构在1.5 m 高度下跌落具有较高的安全性。文献[6]运用有限元分析ANSYS/LS-DYNA 软件对裸态弹丸底向下跌落时的冲击特性进行仿真,总结了裸态弹丸跌落的冲击特性规律,其研究结果表明:同种弹丸、同种材质的跌落目标,跌落冲击时间不随弹丸跌落高度变化而变化,引信跌落冲击峰值与跌落高度的算数平方根近似呈正比。文献[7]以105 mm 口径弹丸为仿真对象,研究了弹丸以不同姿态跌落至不同介质时弹头引信和弹底引信受到的跌落冲击脉冲峰值和宽度。研究结果表明:无论是弹头向上还是弹头向下姿态跌落,弹底引信的跌落冲击脉冲峰值都低于弹头引信。文献[8]对箱装弹药的跌落冲击过程进行了仿真研究,并进行了试验验证,其结果表明:箱装弹药以小角度倾斜跌落地面不会降低弹丸的安全性,可以将堆摞箱数增加至4 箱。虽然已有相关文献采用有限元方法研究了裸态弹丸以不同高度底向下垂直跌落碰撞不同地面目标时作用于引信上的冲击过载特性,但未见有对此过程建立弹塑性模型推导出冲击特性公式的文献。

针对上述问题,本文采用理论推导结合有限元仿真对裸态弹丸底向下垂直跌落碰撞不同地面目标时弹丸和引信的冲击特性进行系统性总结。

1 裸态弹丸底向下垂直跌落碰撞地面目标冲击特性理论公式

1.1 碰撞模型的建立

假设弹丸跌落碰撞的地面目标为弹性半空间体,弹丸质量为,弹丸直径为,弹底直径为,弹体和地面目标的弹性模量分别为和,泊松比分别为和,弹丸与地面目标碰撞中产生的接触压力为,弹丸跌落地面目标示意图如图1 所示。为简化分析,将弹丸看作是一个刚体,弹丸跌落过程则可看作是在直径为的圆面积内均匀受到载荷的作用。

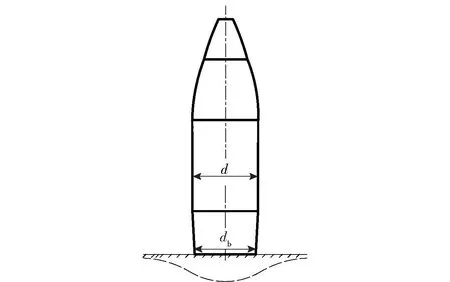
图1 弹丸跌落地面目标示意图Fig.1 Schematic diagram of projectile dropping to the ground

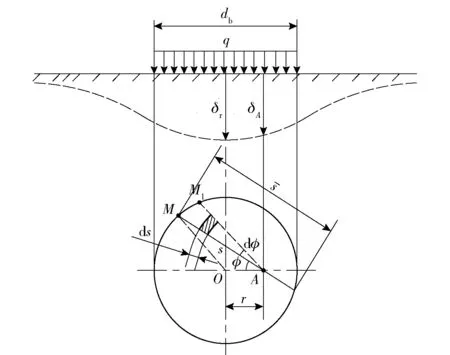
图2 弹丸跌落冲击地面目标时地面目标圆内任意一点A 的下沉量Fig.2 Sinkage of any point A in the ground target circle when the projectile drops and collids the ground target

d上的压力为

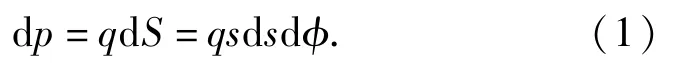
应用叠加法推导出圆形均匀载荷作用下引起的点下沉量,由微元面积d上压力引起的点下沉量为

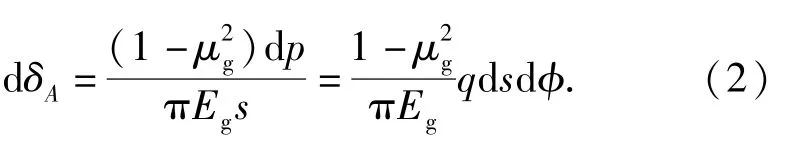
由总压力引起的点下沉量为

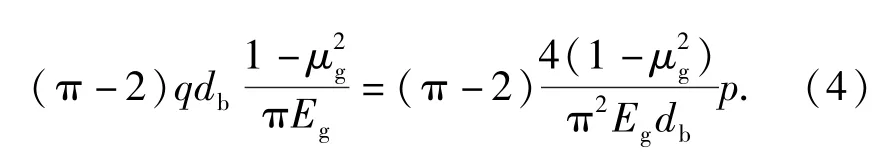
考虑弹丸的变形量,将弹丸简化为一个整体,则总下沉距离为

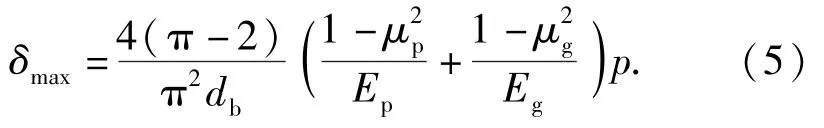
1.2 理论公式推导

文献[10]详细描述了弹丸的跌落冲击过程。弹丸与地面目标碰撞,接触压力使弹丸减速运动,设弹丸的速度为,根据牛顿第二定律建立微分运动方程:

弹丸与地面目标的相对速度为

将(7)式两边对时间求导,

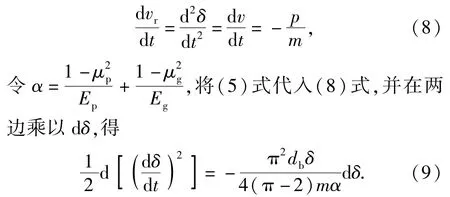
令碰撞开始时弹丸与靶板的相对速度为,开始碰撞进行压缩时的相对速度为=dd,将(9)式积分,得

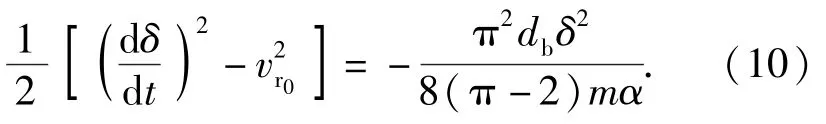
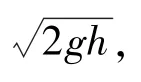
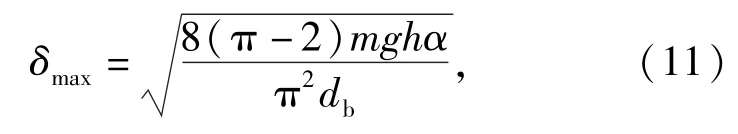
令(5)式与(11)式相等,即

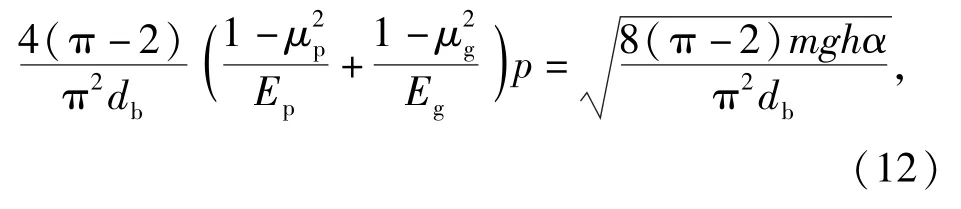
进而可以得到弹丸跌落产生的冲击加速度峰值为

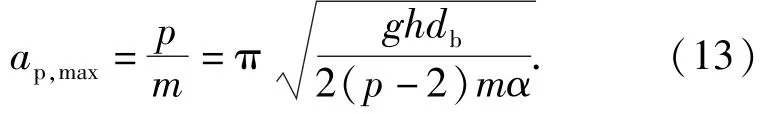
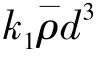
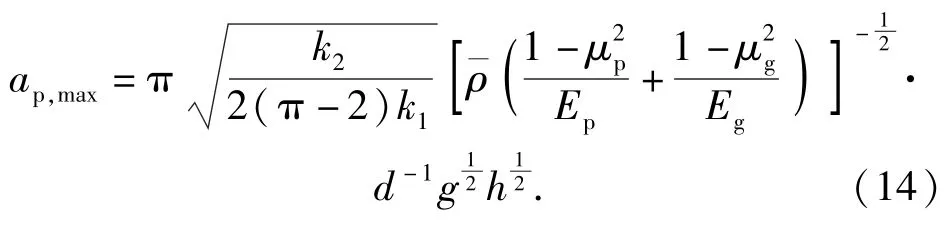
从(14)式中可以看出,弹丸与地面目标碰撞,弹丸的冲击加速度峰值与跌落高度的算术平方根呈正比,与弹丸直径呈反比。

由(10)式可得

弹丸跌落地面目标是一个非弹性碰撞过程,假设弹体与地面目标之间的碰撞恢复系数为,无量纲,则碰撞恢复时间为

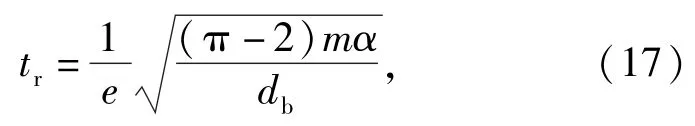
则总冲击作用时间为

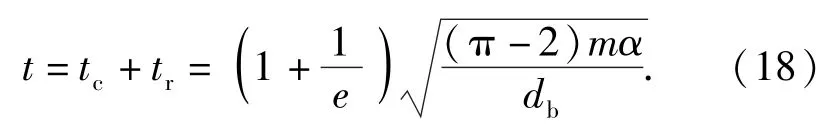
同(13)式、(14)式的推导方法进行化简,可得到

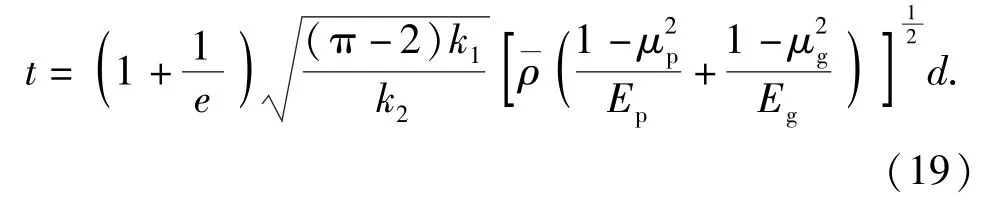
从(19)式中可以看出,弹丸与地面目标碰撞,弹丸冲击作用时间与弹丸直径呈正比,与跌落高度无关。

(14)式和(19)式即为裸态弹丸底向下垂直跌落碰撞地面目标时,弹丸整体冲击加速度峰值与冲击作用时间的理论推导公式。

2 弹丸底向下垂直跌落碰撞地面目标时的弹丸和引信冲击特性仿真

2.1 建立有限元模型

为了对第1 节的理论推导公式进行验证,选择某152 mm 口径榴弹作为仿真对象,建立裸态弹丸垂直跌落有限元模型。由于弹丸和引信结构复杂,为减少计算时间,将模型进行简化配重处理,简化后的弹丸模型如图3 所示。

图3 152 mm 口径榴弹简化模型Fig.3 Simplified model 152 mm caliber HE-projectile

参照国家军用标准GJB 537A—1998 引信环境与性能试验方法中的104 要求,装有全备引信的试验弹或裸态的全备引信跌落到钢板上,钢板最小厚度为75 mm,布氏硬度不低于200,且应牢固地安装在厚度不小于0.6 m 的混凝土基座上。钢板表面必须平整,长、宽尺寸至少为试验弹最大尺寸的1.0～1.5 倍。文献[6]仿真表明,有无混凝土基座对跌落冲击峰值和冲击时间基本无影响,故本文仿真为节省机时省略了混凝土基座。因为裸态弹丸最大尺寸为707 mm,所以设置跌落目标靶板长、宽均为1 062 mm。国家军用标准GJB 573A—1998 引信环境与性能试验方法中除了规定1.5 m 高度跌落试验外,还规定可采用其他高度及对除钢板以外的地面目标进行跌落试验。

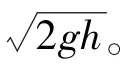
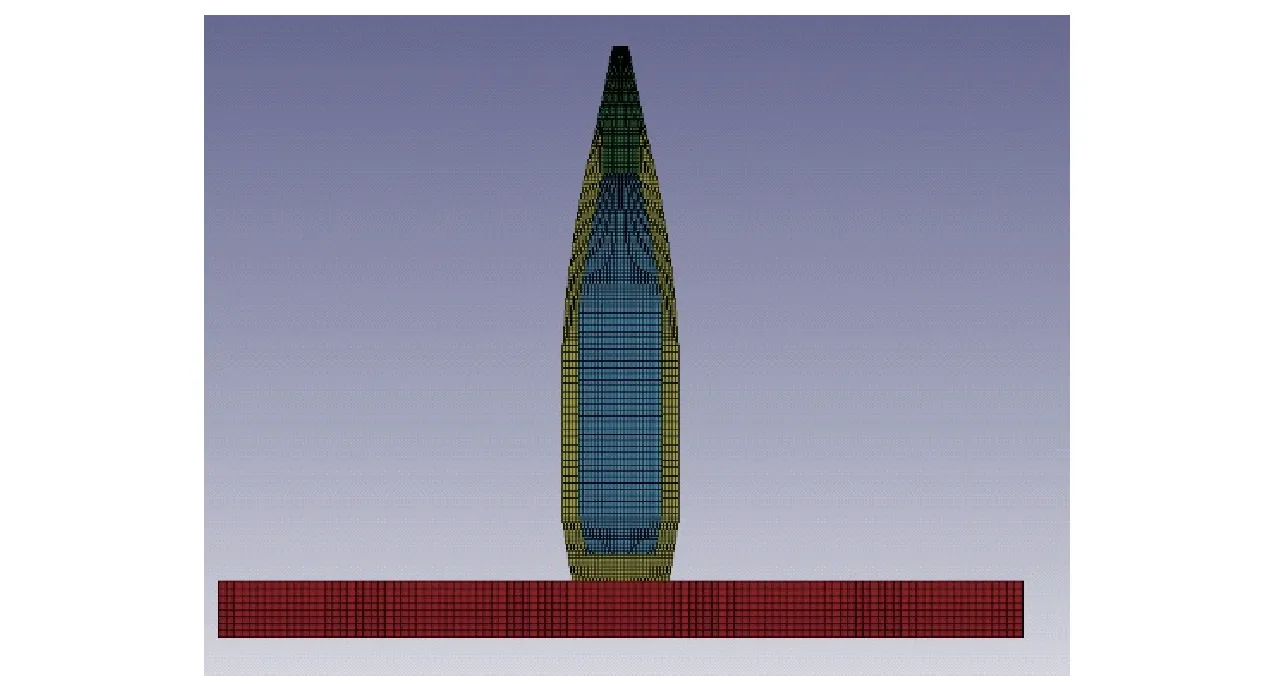
图4 弹丸跌落有限元模型Fig.4 Finite element model of projectile dropping

引信体材料为7A04 铝合金,弹体材料为D60 钢。引信、弹体和钢板采用JOHNSON_COOK 材料模型,装药、混凝土、红松木板和土壤均采用PLASTIC_KINEMATIC材料模型。各材料仿真参数如表1 所示,152 mm 口径弹丸相关参数如表2 所示。

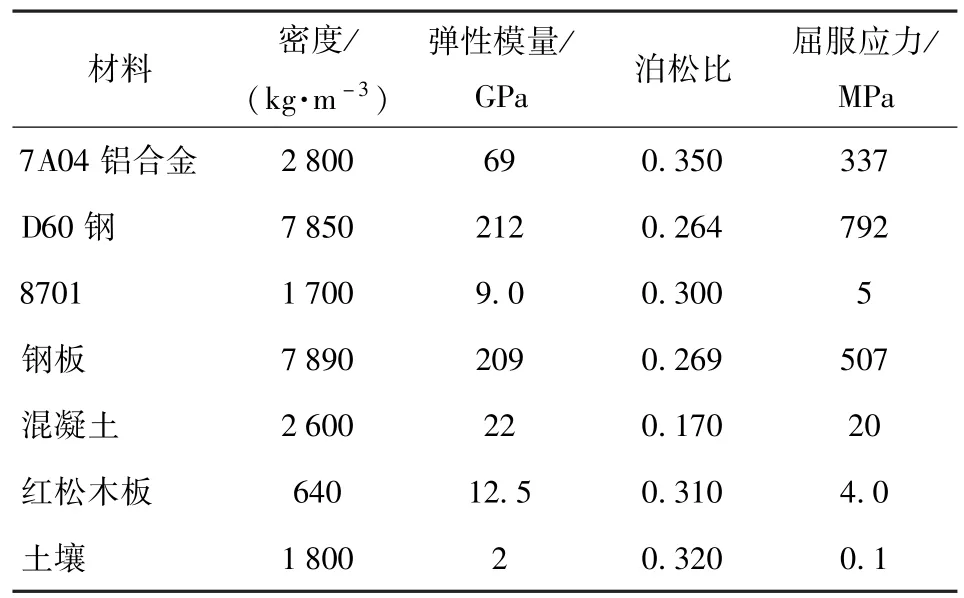
表1 各材料仿真参数[12-14]Tab.1 Simulation parameters of various materials[12-14]

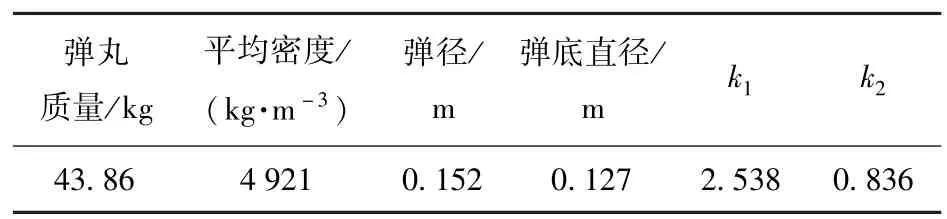
表2 152 mm 口径弹丸相关参数Tab.2 Related parameters of 152 mm caliber projectile

2.2 弹丸跌落冲击特性

仿真得到152 mm 口径榴弹底向下以0.7 m、1.5 m、2.1 m、3.0 m 落高,分别垂直跌落于钢板、混凝土、红松木、土壤(厚度取为75 mm)时,弹丸跌落冲击加速度峰值如表3 所示,弹丸冲击作用时间如表4 所示。

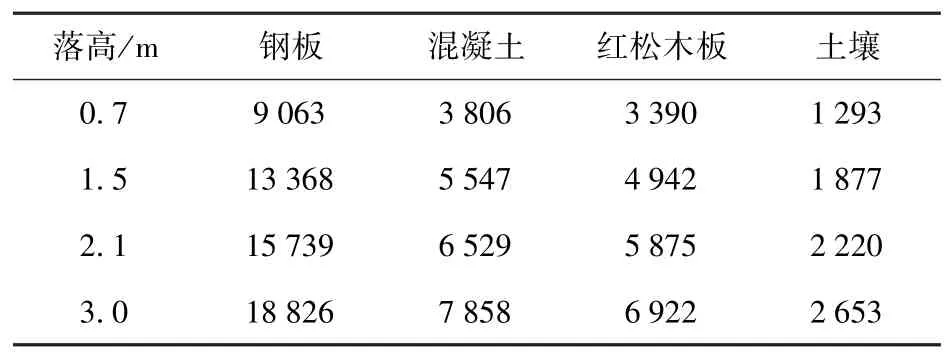
表3 152 mm 口径弹丸以不同落高底向下垂直跌落时弹丸跌落冲击加速度峰值Tab.3 Peak impact acceleration of 152 mm caliber projectile when vertically dropping at different heights g

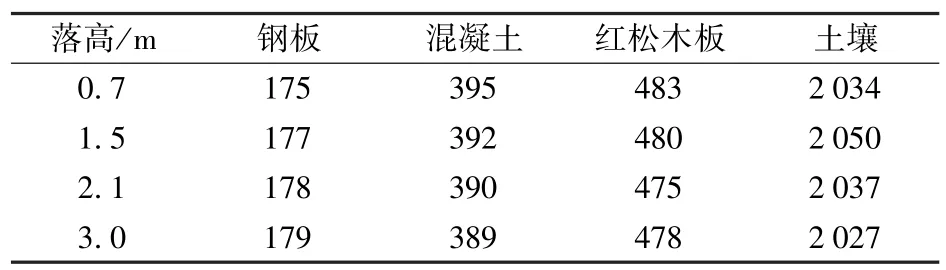
表4 152 mm 口径弹丸以不同落高底向下垂直跌落时弹丸跌落冲击作用时间Tab.4 Impact duration of 152 mm caliber projectile when vertically dropping at different heights μs

从表3 和表4 中可以看出:裸态弹丸以同一高度跌落时,弹丸冲击峰值随跌落介质硬度增大而增大,跌落冲击时间随着跌落介质硬度增大而减小;不同高度跌向同一介质时,弹丸跌落冲击峰值随跌落高度增大而增大,跌落冲击时间基本不随高度变化而变化。

由于受飞行稳定性限制,旋转弹丸弹形和长径比相差不太大,可将该152 mm 口径榴弹弹丸等比例缩小成为122 mm、85 mm、57 mm、37 mm、20 mm共5 种口径榴弹弹丸(由于弹丸质量与弹丸直径的3 次方呈比例,质量也相应减小),分别从不同高度跌落至钢板、混凝土、红松木板和土壤,弹丸跌落冲击加速度峰值仿真结果如表5 所示。

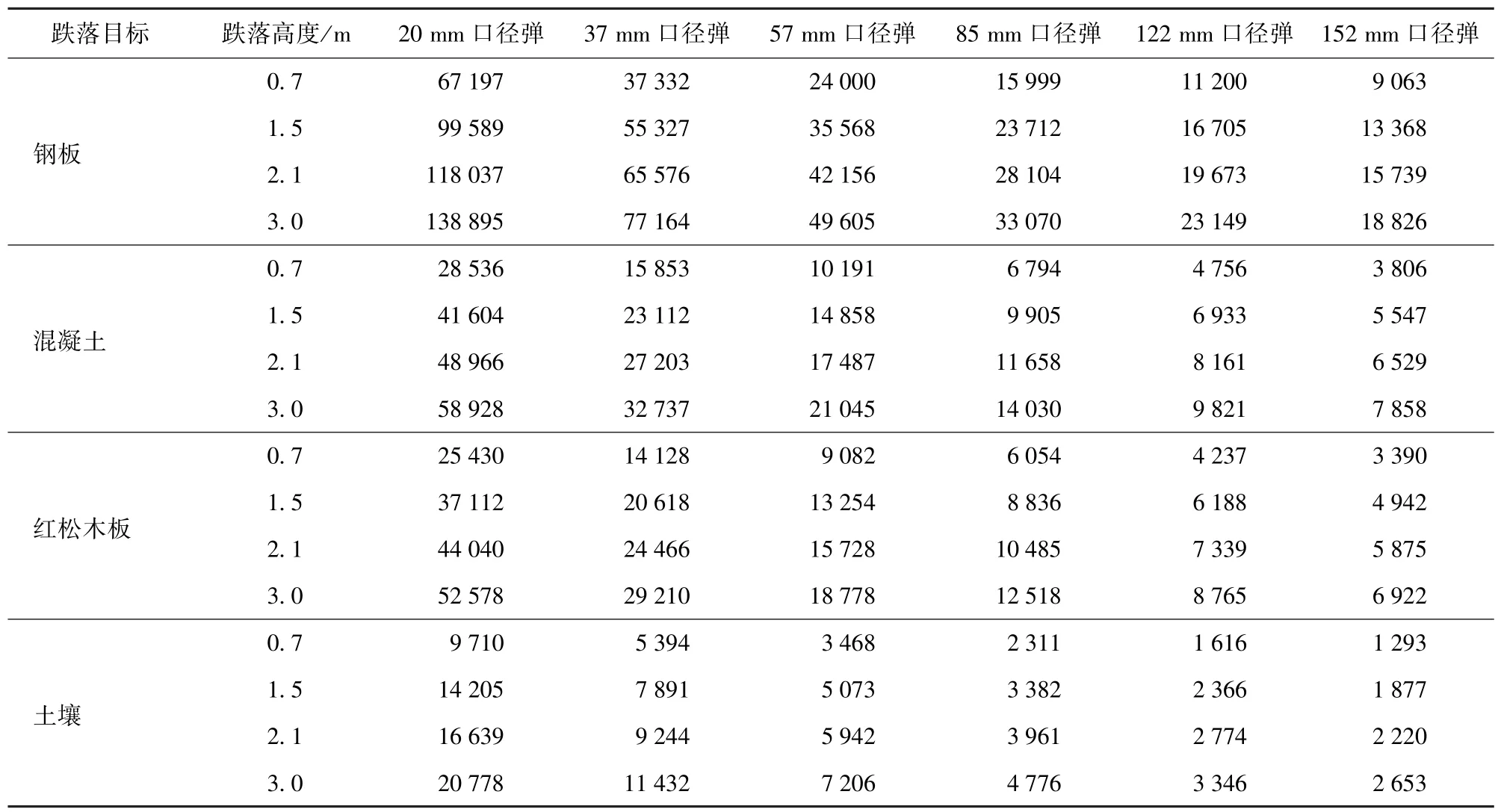
表5 不同口径弹丸以不同高度垂直跌落于不同地面目标时的弹丸冲击加速度峰值Tab.5 Peak impact acceleration of projectiles with different calibers dropping vertically on different ground targets at different heights g

比较表5 中的数据可以看出,在弹形相同条件下,弹丸以相同跌落高度跌落同一地面目标时,跌落冲击峰值随着弹丸直径的增大而减小。

为了初步验证弹丸跌落冲击特性理论公式的可信性,引入一个加速度修正系数,假设弹丸跌落时产生的冲击加速度峰值为

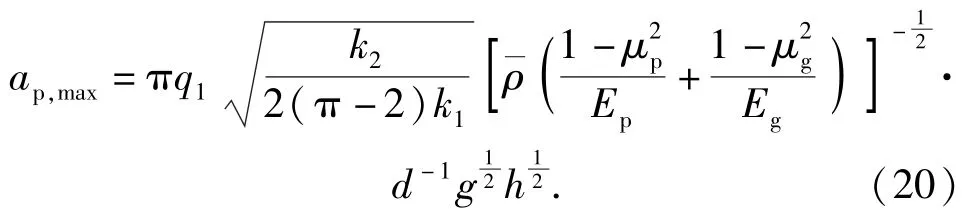
将表1 和表2 中各参数代入(20)式进行拟合,表6 为通过理论公式计算并拟合得到的加速度修正系数。由表6 可知,弹丸跌落至地面目标的冲击加速度峰值理论修正公式中加速度修正系数可取0.884～1.027 0,平均值为0.94这主要是由于在计算弹丸跌落变形量时将弹丸简化为一个整体,取为弹体弹性模量而不是弹丸平均弹性模量,从而导致偏大,弹丸最大加速度计算值偏高,修正系数值偏小。将该平均值代入(20)式,可以得到弹丸跌落地面目标时的冲击加速度峰值修正公式为

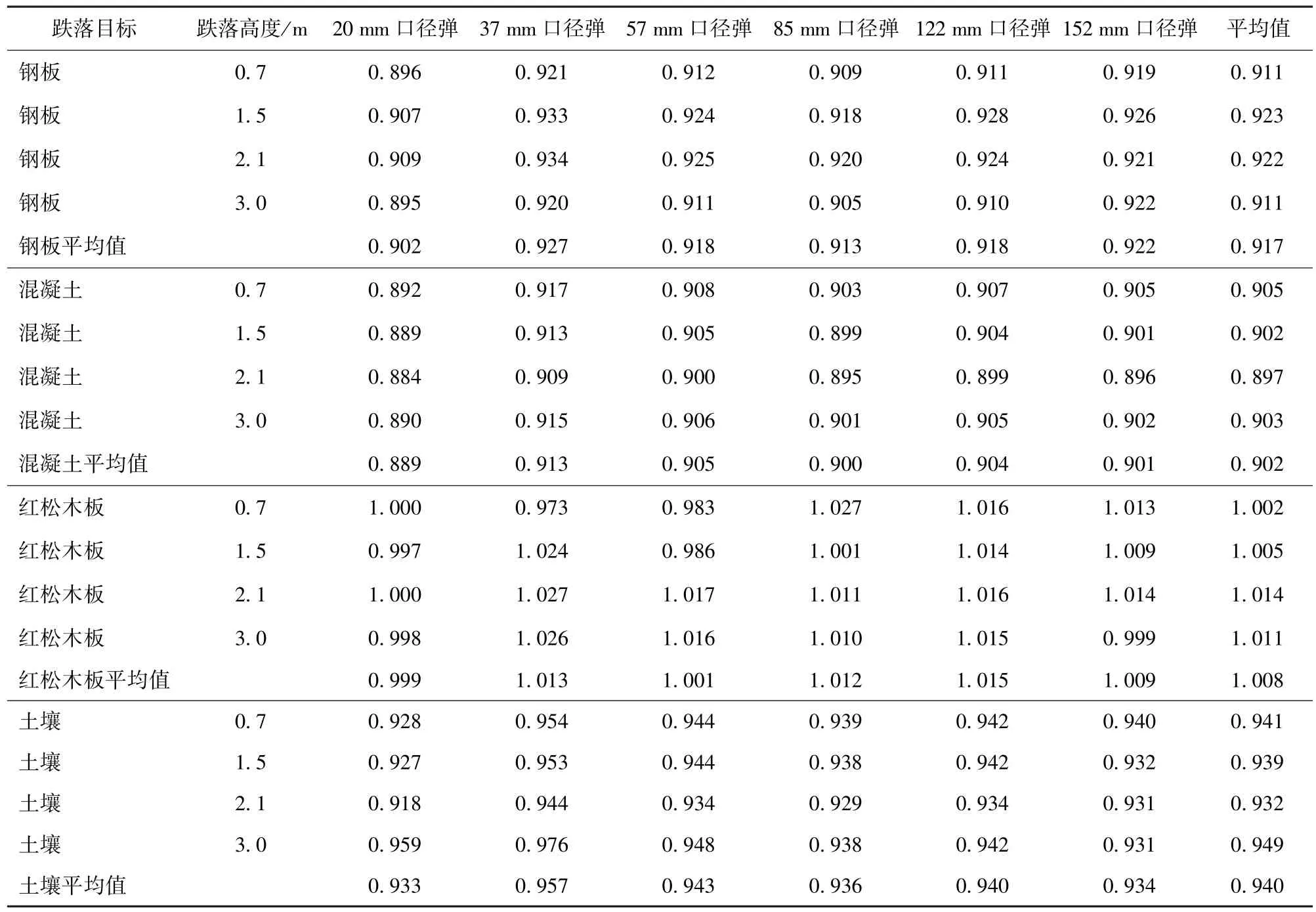
表6 通过理论公式拟合得到的加速度修正系数q1Tab.6 Acceleration correction coefficients q1 obtained by fitting the theoretical formula

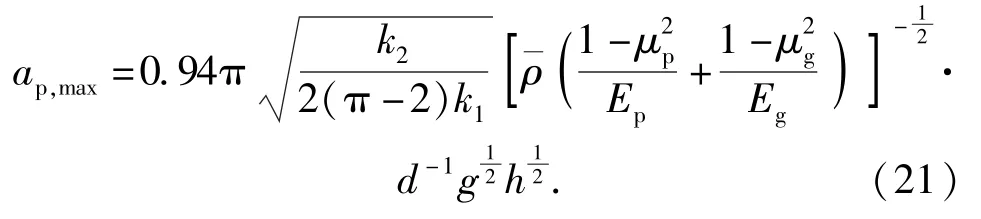
6 种不同口径弹丸从不同高度跌落至钢板、混凝土、红松木板和土壤时,弹丸的跌落冲击作用时间仿真结果如表7 所示。

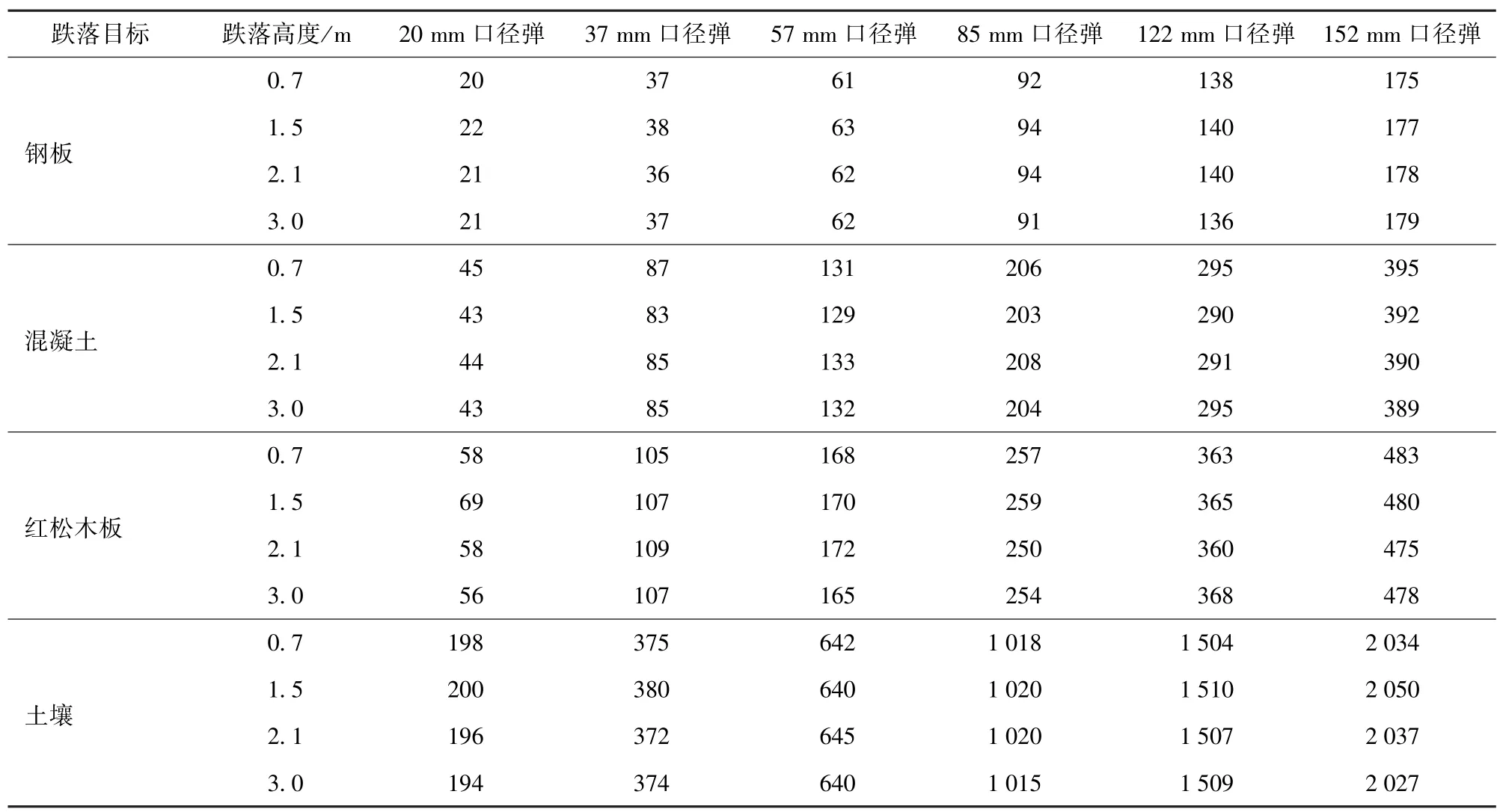
表7 不同口径弹丸以不同高度垂直跌落于不同地面目标时的冲击作用时间Tab.7 Impact duration of projectiles with different calibers dropping vertically on different ground targets at different heights μs

从表7 中可以看出:同种弹丸跌落至同一地面目标时,冲击作用时间基本不随高度的变化而变化,与文献[6]仿真得到的结论基本相同;在弹形相同条件下,弹丸以相同跌落高度跌落同一地面目标时,冲击作用时间随着弹丸直径的增大而增大。

同理引入一个冲击时间修正系数,假设弹丸跌落时产生的冲击作用时间为

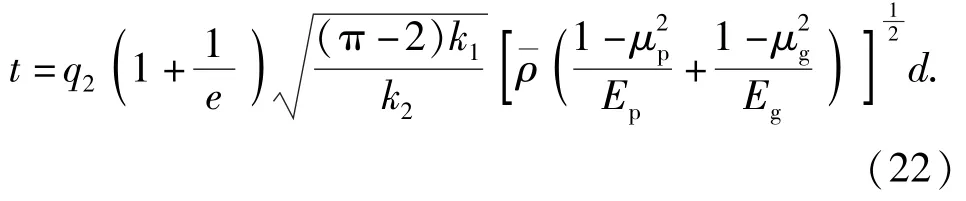
对弹丸跌落地面目标全过程进行分析,根据动量守恒定理,得

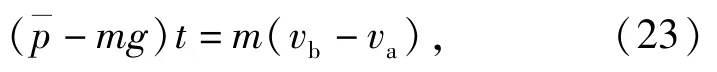
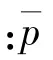
弹丸碰撞地面目标时产生的平均接触压力远大于重力,因此通常忽略重力的影响,(23)式可化简为

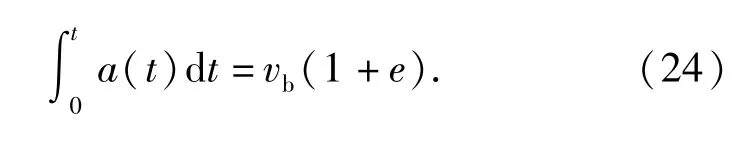
对仿真得到的弹丸跌落冲击加速度曲线()进行积分并利用(24)式进行计算,可求出此次不同口径弹丸跌落钢板、混凝土、红松木和土壤的碰撞恢复系数。表8 为不同口径弹丸以1.5 m 高度垂直跌落碰撞不同地面目标时的碰撞恢复系数。由表8可以看出:对于弹丸以同一高度跌落碰撞同种地面目标,碰撞恢复系数随着弹丸口径的增大而减小;冲击作用时间基本不随高度变化而变化,因此对同一弹丸以不同高度跌落得到的冲击时间取平均值。

表8 不同口径弹丸以1.5 m 高度垂直跌落碰撞不同地面目标时的碰撞恢复系数Tab.8 Collision recovery coefficients of different caliber projectiles colliding with different ground targets

将表1 和表2 中各参数代入(22)式进行拟合,正系数。

由表9 可以看出,弹丸跌落地面目标时产生的表9 为通过理论公式计算并拟合得到的冲击时间修冲击作用时间理论修正公式中系数可取1.005～1.070,平均值为1.04。由于取为弹体弹性模量而不是弹丸平均弹性模量,从而导致偏大,弹丸冲击时间计算值偏短,修正系数值偏大。将该平均值代入(22)式,可以得到弹丸跌落地面目标的冲击作用时间修正公式为

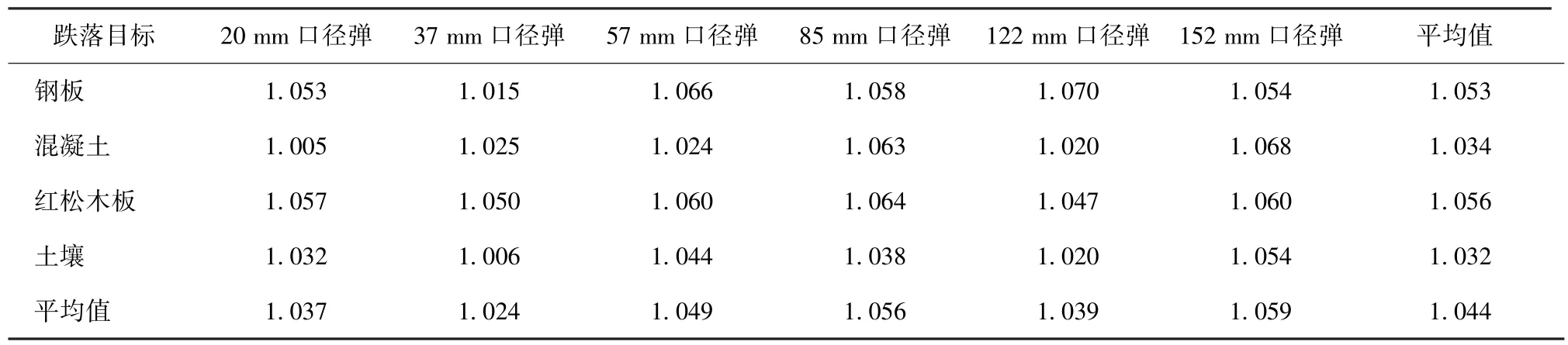
表9 通过理论公式拟合得到的时间修正系数q2Tab.9 Time correction coefficients q2 obtained by fitting the theoretical formula

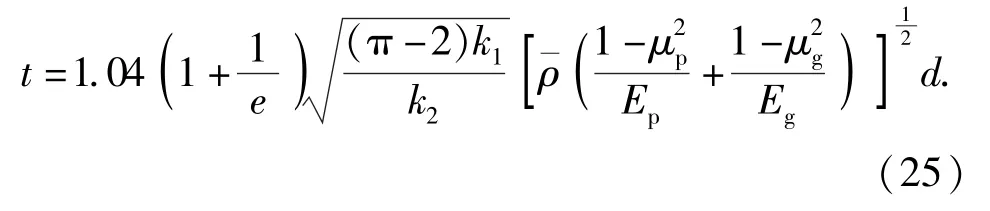
(21)式和(25)式即为弹丸跌落地面目标时冲击加速度峰值与冲击作用时间的修正公式,从中可以发现,通过仿真得到弹丸冲击特性规律与通过理论推导得到的弹丸跌落冲击特性规律相近,即冲击加速度峰值与弹丸直径和跌落高度有关,冲击作用时间与弹丸直径有关而与跌落高度无关,可认为弹丸冲击特性理论公式通过修正具有一定可信性。

2.3 弹丸跌落时的引信冲击特性

6 种不同口径弹丸从不同高度跌落至钢板、混凝土、红松木板和土壤,其引信跌落冲击加速度峰值仿真结果如表10 所示,跌落冲击作用时间仿真结果如表11 所示。

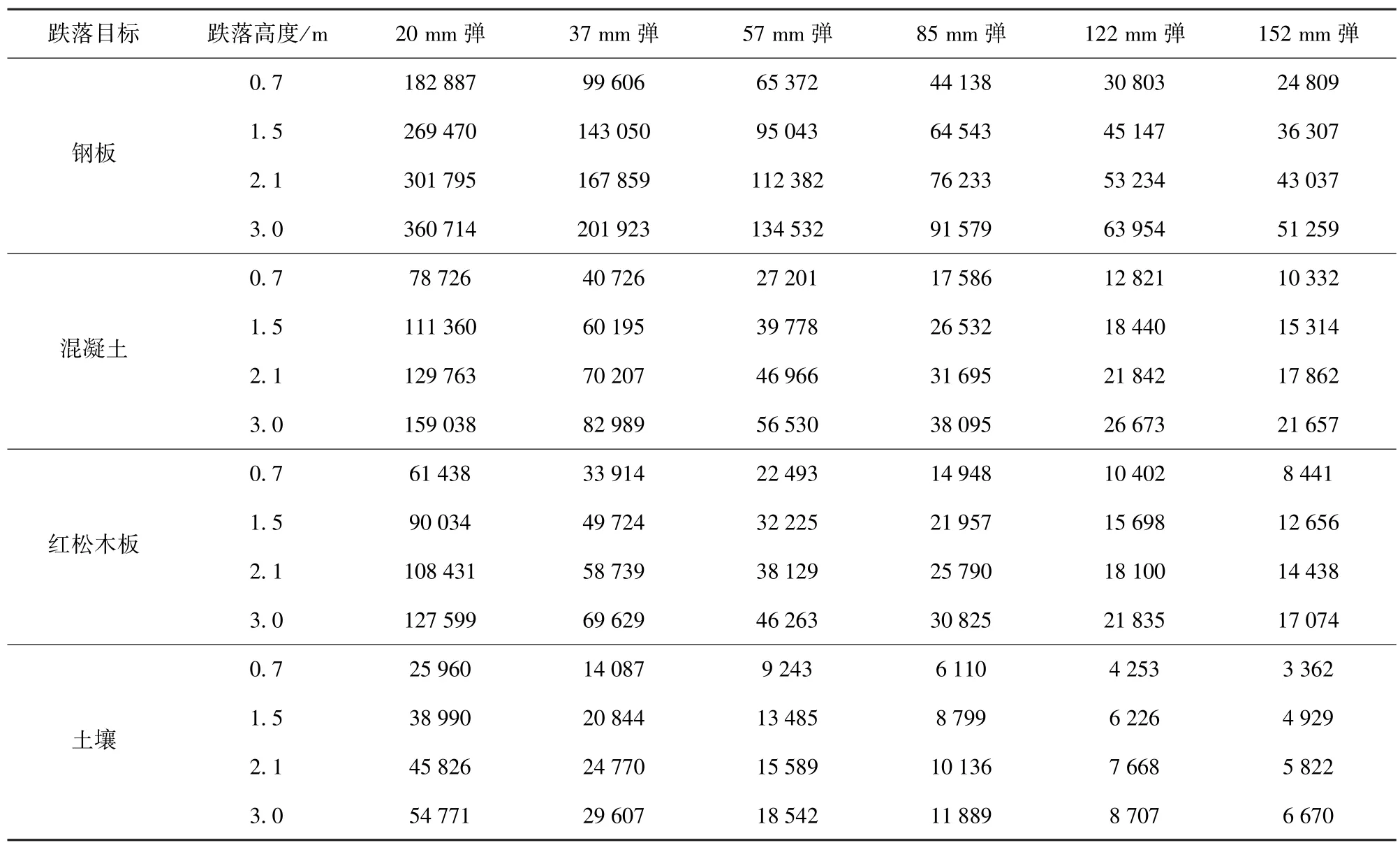
表10 不同口径弹丸以不同高度垂直跌落于不同地面目标时的引信冲击加速度峰值Tab.10 Peak fuze impact acceleration of different caliber projectiles dropping on different ground targets at different heights g

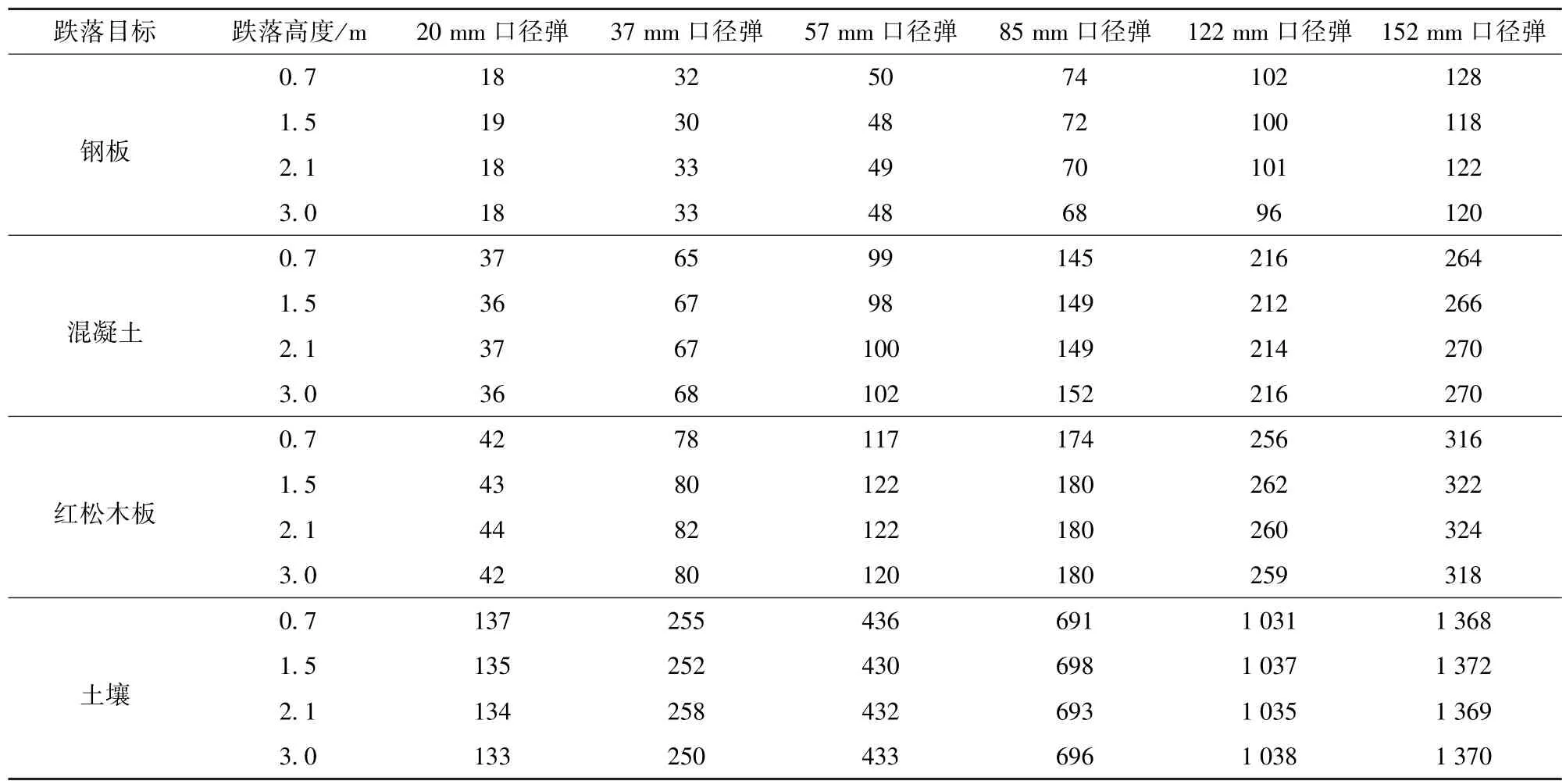
表11 不同口径弹丸以不同高度垂直跌落于不同地面目标的引信冲击作用时间Tab.11 Fuze impact durations of different caliber projectiles dropping vertically on different ground targets at different heights μs

由表10 和表11 中可以看出,通过仿真得到引信冲击特性规律与弹丸跌落冲击特性规律相近,下面将拟合得到弹丸底向下垂直跌落时引信冲击特性的计算公式。

假设引信跌落加速度峰值与弹丸跌落加速度冲击峰值呈比例关系,现引入一个新的加速度比例系数,引信跌落冲击加速度峰值可写为

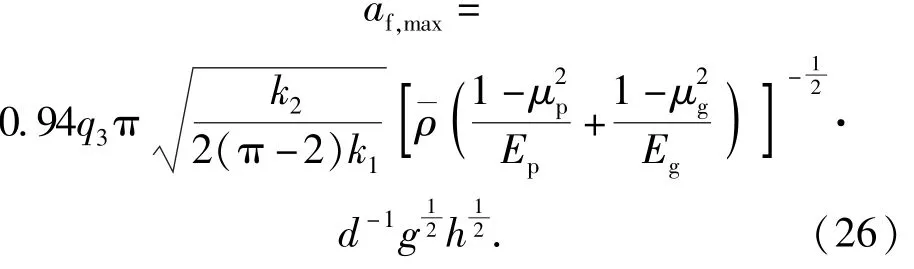
为了求得加速度比例系数,将表1 和表2 中各材料参数代入(26)式进行拟合。表12 为通过修正公式计算并拟合得到的加速度比例系数。

由表12 可知,弹丸跌落地面目标时引信的冲击加速度峰值计算公式中比例系数可取2.400～2.759,平均值为2.61,即弹丸底向下垂直跌落至地面目标时,引信冲击加速度峰值大约是弹丸加速度峰值的2.61倍,将该平均值代入(26)式可以得到弹丸跌落地面目标时的引信冲击加速度峰值计算公式为

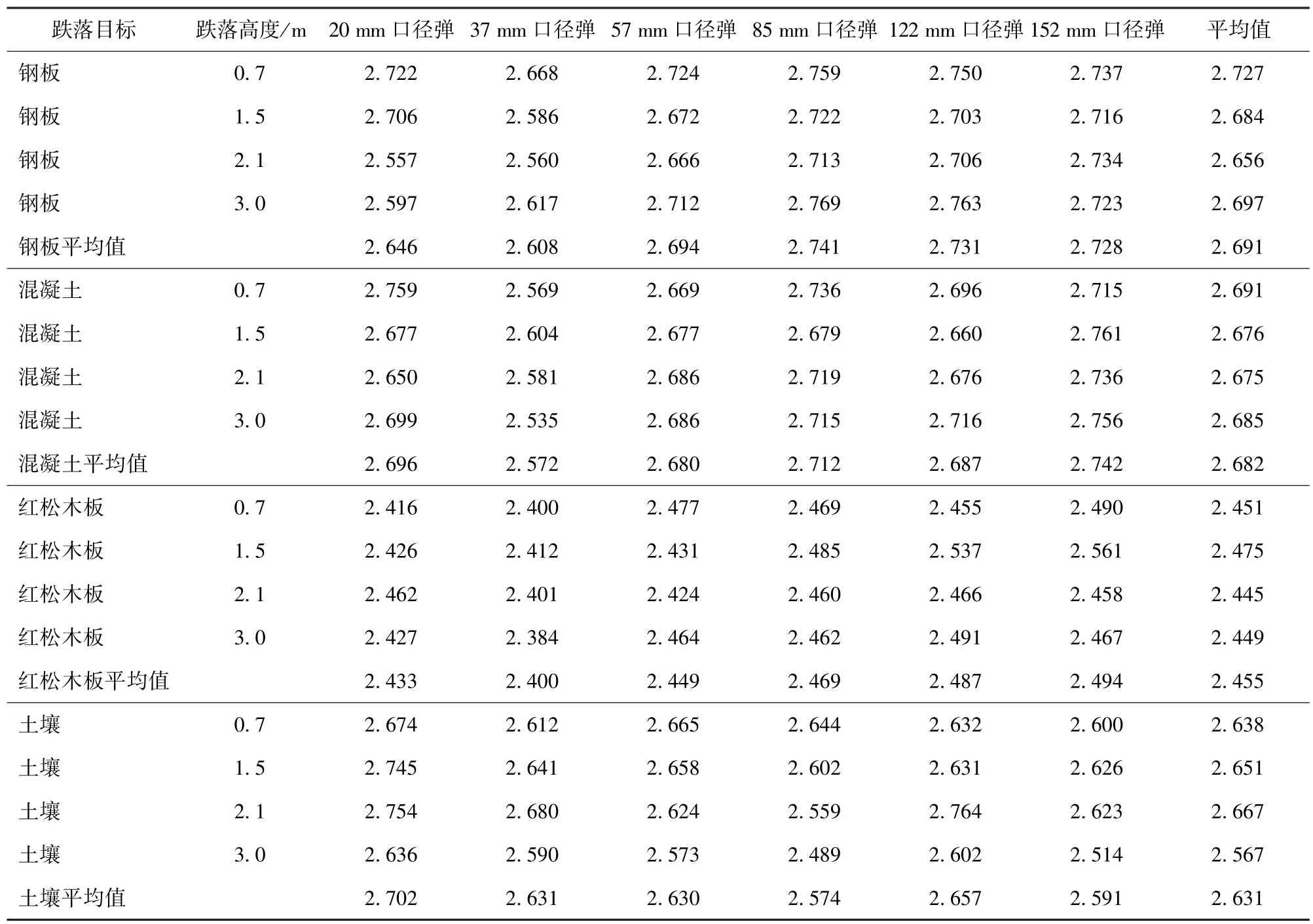
表12 通过修正公式拟合得到的加速度比例系数q3Tab.12 Acceleration proportionality coefficients q3 obtained by fitting the correction formula

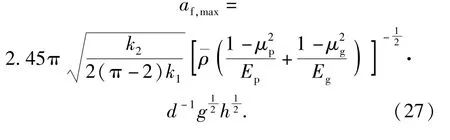
同理,假设引信跌落冲击时间与弹丸跌落冲击时间呈比例关系,引入一个新的冲击时间比例系数,引信的冲击作用时间可写为

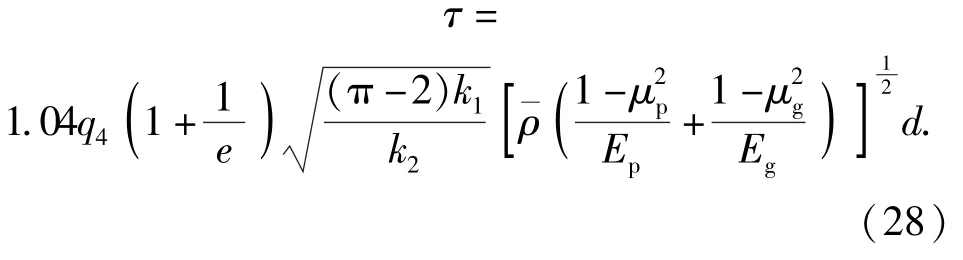
将表1 和表2 中各参数代入(28)式进行拟合,表13 为通过修正公式计算并拟合得到的冲击时间比例系数。

由表13 可以看出,弹丸跌落地面目标时引信的冲击作用时间计算公式中系数可取0.665～0.837,平均值为0.73,即弹丸底向下垂直跌落至地面目标时,引信冲击作用时间大约是弹丸冲击作用时间的0.73 倍。将该平均值代入(28)式可以得到弹丸跌落地面目标时的引信冲击作用时间公式为

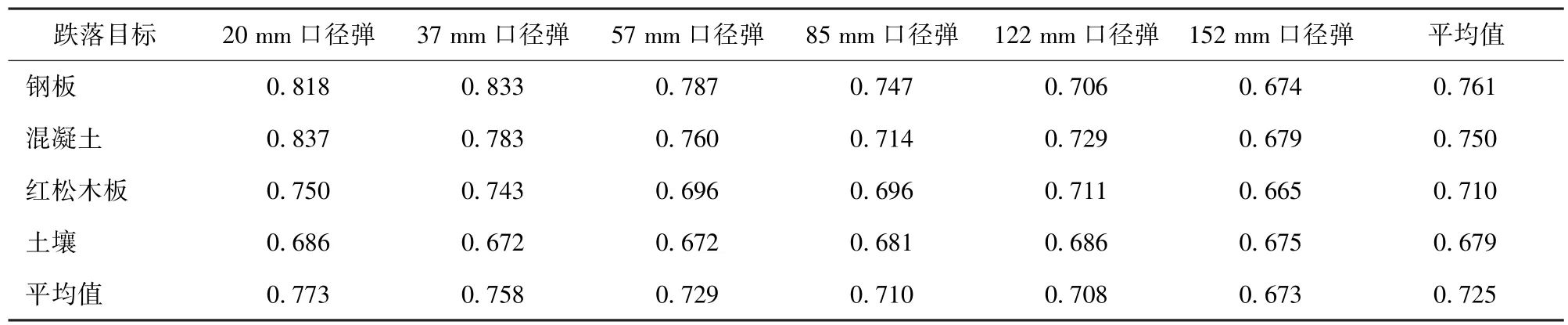
表13 通过修正公式拟合得到的冲击作用时间比例系数q4Tab.13 Impact duration proportional coefficients q4 obtained by fitting the modified formula

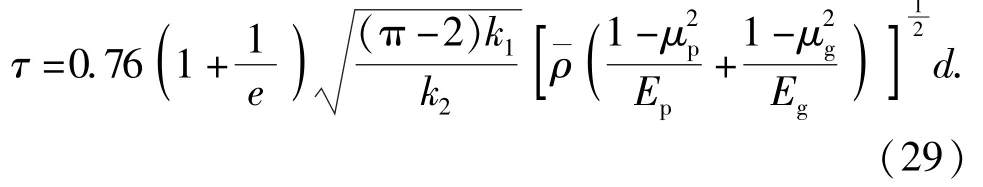
至此就得到了弹丸底向下跌落时引信冲击加速度峰值和冲击作用时间的计算公式。需要注意的是,该公式适用范围为配用于平底弹丸的弹头引信。

2.4 不同参数对引信冲击特性的影响

从(27)式和(29)式可以看出:引信冲击加速度峰值与弹丸平均密度、弹体的泊松比、弹体的弹性模量、地面目标的泊松比、地面目标的弹性模量、跌落高度以及弹丸直径有关;冲击作用时间与碰撞恢复系数、弹丸平均密度、弹体的泊松比、弹体的弹性模量、地面目标的泊松比、地面目标的弹性模量以及弹丸直径有关。下面仍以152 mm 口径榴弹为例,分析计算公式中各参数对引信冲击特性的影响。

改变弹丸平均密度,采用计算公式求得弹丸以1.5 m 落高跌落钢板时引信冲击加速度峰值与作用时间变化,如图5 所示。由图5 可以看出,弹丸平均密度越大,弹丸跌落时产生的引信冲击加速度峰值越小,相应的冲击作用时间越长,但影响程度有限。

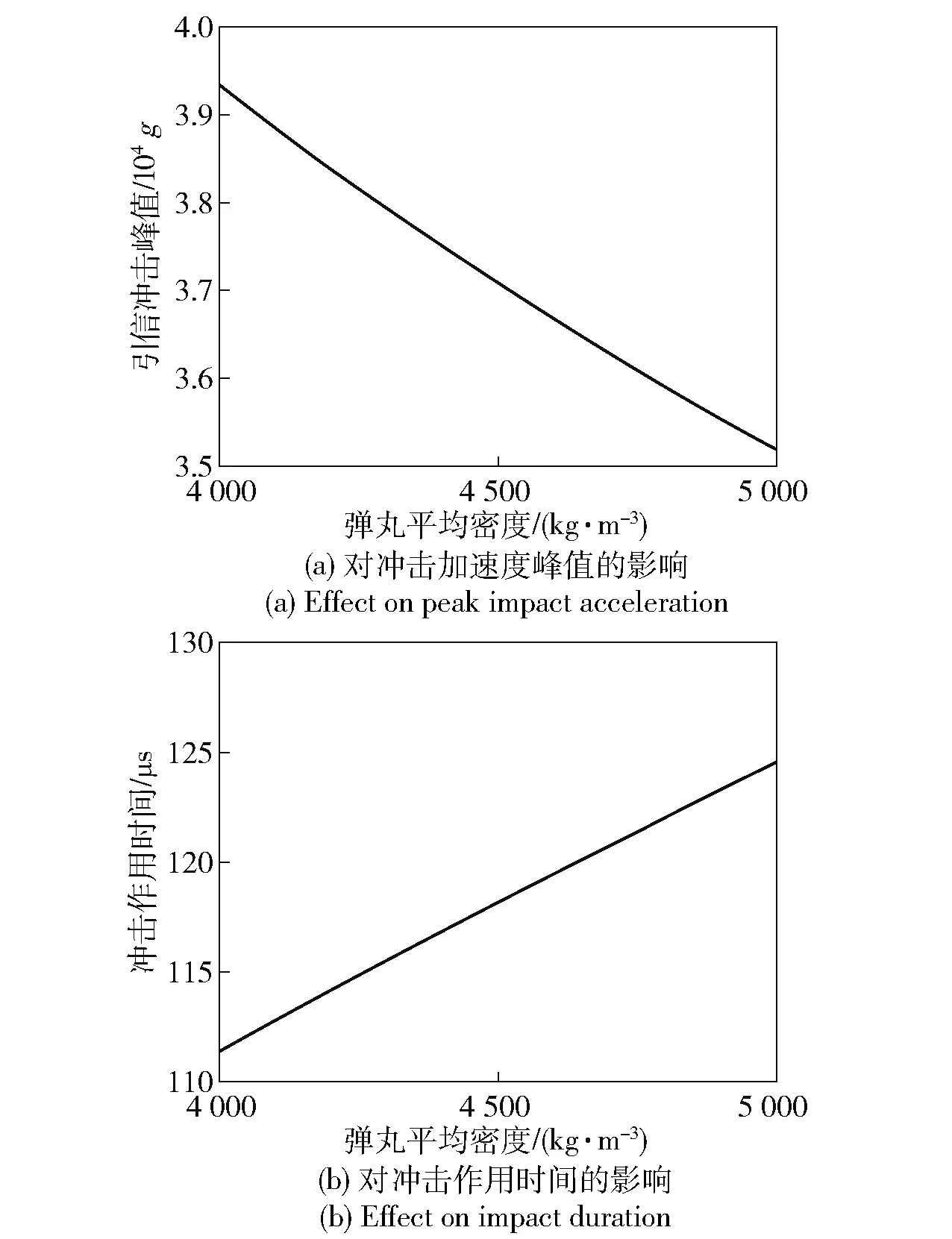
图5 弹丸平均密度对引信冲击特性的影响Fig.5 Effect of projectile average density on impact characteristics of fuze

通常材料的泊松比取值范围为0～0.5,改变地面目标泊松比,采用计算公式求得弹丸以1.5 m 落高跌落钢板时引信冲击加速度峰值与作用时间变化,如图6 所示。地面目标的泊松比越大,弹丸跌落时产生引信的冲击加速度峰值越大,冲击时间越短,但影响程度非常有限,可以忽略不计。

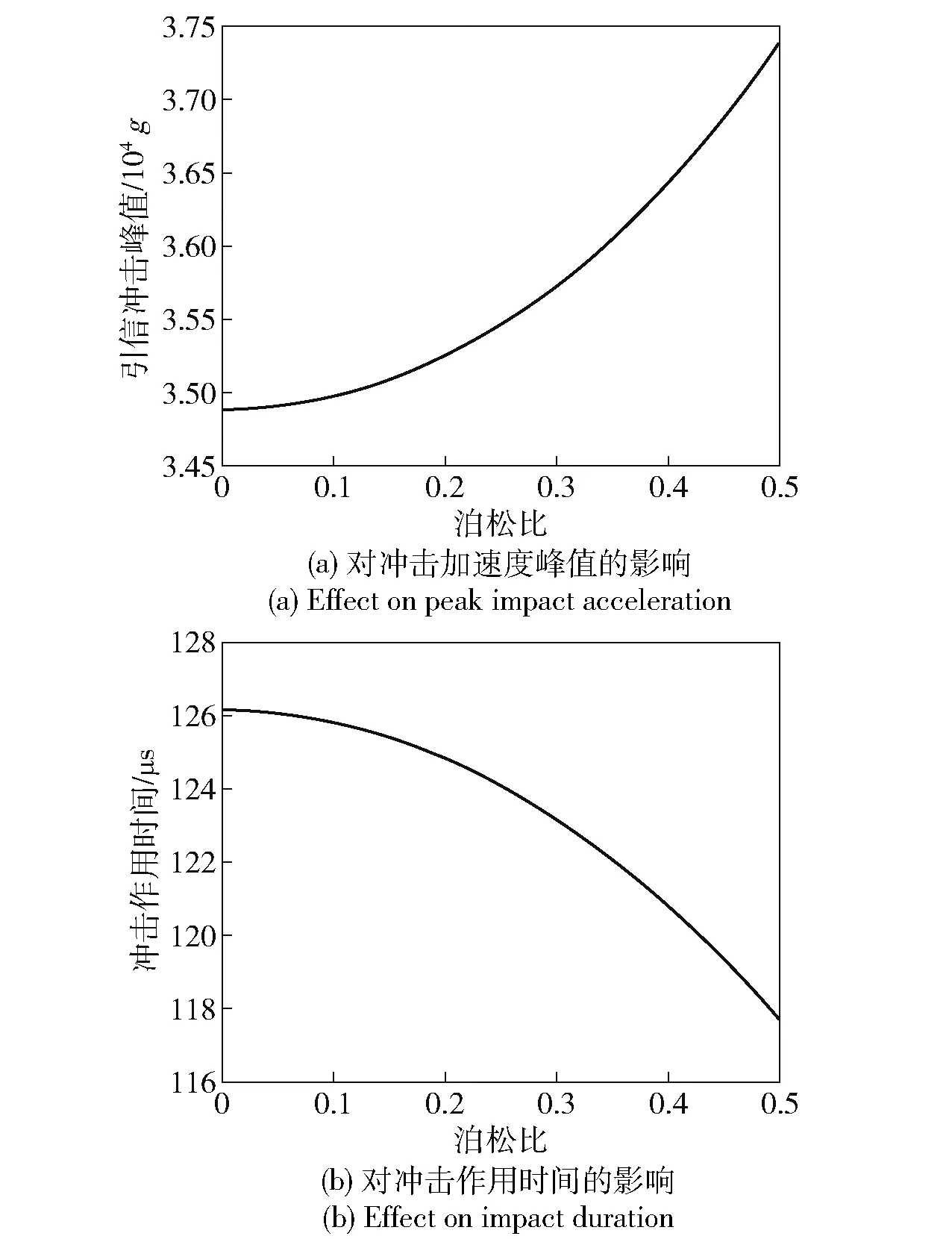
图6 地面目标泊松比对引信冲击特性的影响Fig.6 Effect of poisson's ratio of ground target on impact characteristics of fuze

改变地面目标的弹性模量,采用计算公式求得弹丸以1.5 m 落高跌落不同地面目标时引信冲击加速度峰值与作用时间变化,如图7 所示。由图7 可见,地面目标的弹性模量对引信冲击特性影响程度巨大,弹性量越大,弹丸跌落时产生引信的冲击加速度峰值越大,冲击时间越短。

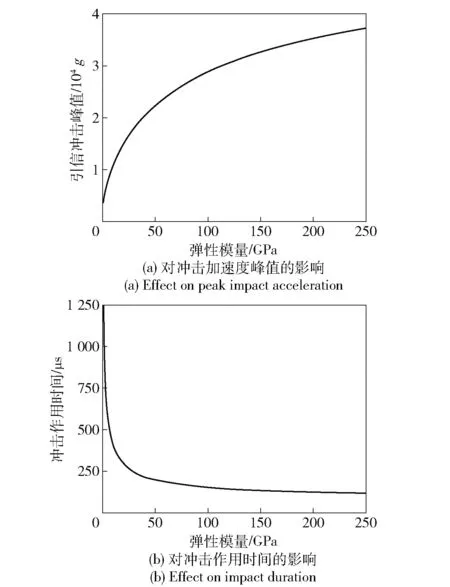
图7 地面目标弹性模量对引信冲击特性的影响Fig.7 Effect of ground target elastic modulus on impact characteristics of fuze

从(27)式和(29)式的形式可以看出,弹体材料与地面目标材料的影响程度是相同的,因此上述规律对弹体材料同样适用。

通过计算公式与仿真表明,弹丸直径影响跌落时的引信冲击特性,弹丸直径越大,跌落时产生的冲击峰值越小,冲击作用时间越长;弹丸直径越小,冲击峰值越大,冲击时间越短;弹丸跌落碰撞地面目标时,跌落高度仅改变冲击加速度峰值大小,跌落高度越高,引信冲击加速度峰值越大;碰撞恢复系数仅改变冲击作用时间的长短,二者的碰撞恢复系数越大,碰撞时间越短。

(30)式为引信冲击加速度峰值与冲击作用时间计算公式的乘积,该公式较为简洁。

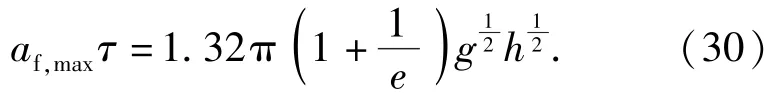
假设弹丸跌落碰撞地面目标过程为完全弹性碰撞,则=1,进而(30)式可进一步化简为

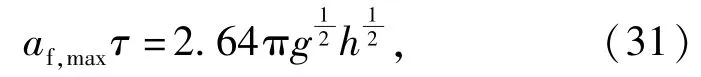
即二者的乘积仅与跌落高度有关,即在完全弹性碰撞的情况下,弹丸以同一高度跌落至任意目标,冲击加速度峰值与冲击作用时间乘积是恒定不变的。

3 算例验证

文献[6]给出了100 mm 口径平底榴弹底向下以不同落高垂直跌落钢板的引信冲击加速度和冲击时间仿真数据。文献[15]将不同口径的试验弹从1.5 m 高度以底向下姿态自由跌落到钢板上,通过安装在引信部位的传感器测量并记录每种试验弹丸引信部位的冲击加速度信号。利用本文得到的计算公式分别计算文献[6]中100 mm 口径弹丸与文献[15]中3 种不同口径平底弹丸(76 mm 弹、85 mm弹和122 mm 弹)的引信冲击加速度峰值和冲击作用时间,对比结果如表14 和表15 所示。

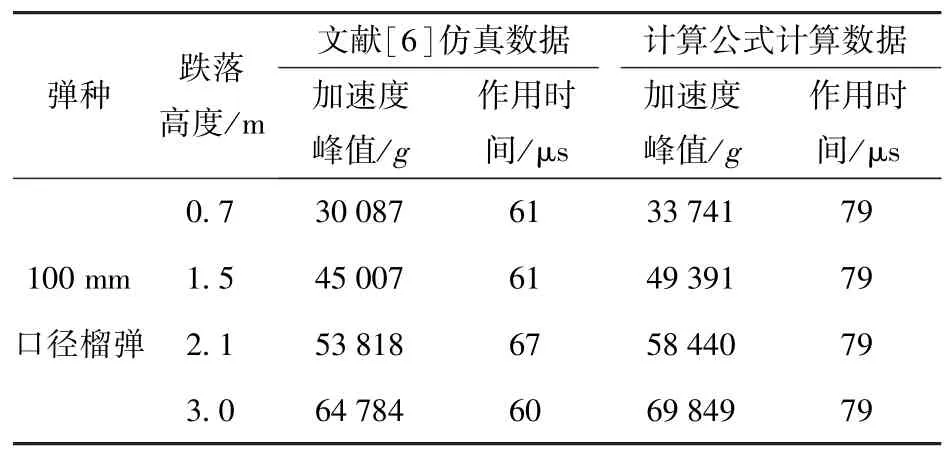
表14 计算公式与仿真结果对比Tab.14 Comparison of calculated and simulated results

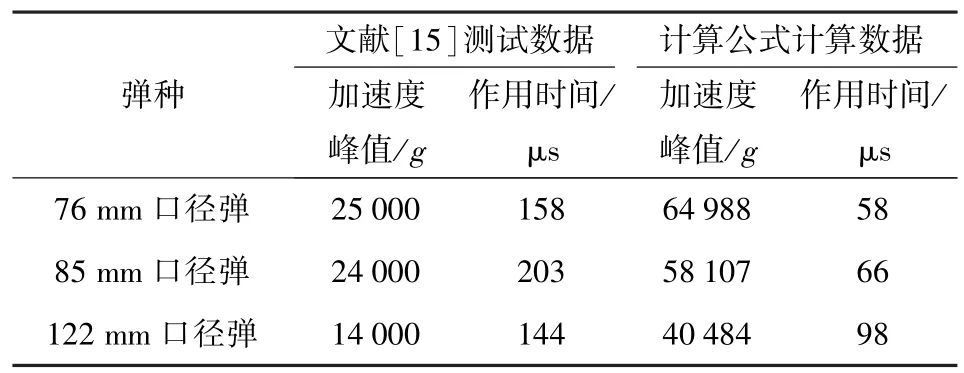
表15 计算公式与测试结果对比Tab.15 Comparison of calculated and test results

由表14 和表15 可以看出,(27)式和(29)式的计算结果与仿真结果相近,误差在可接受范围内;计算加速度峰值偏大于测试数据,而作用时间结果偏小于测试数据。文献[6]仿真结果表明,弹丸由垂直跌落到1°倾角,冲击峰值迅速减小。对文献[6]所给出35 mm、100 mm、130 mm 3 种不同口径榴弹跌落仿真数据进行处理,利用MATLAB 软件拟合得到引信跌落冲击峰值相对衰减量随倾斜角度变化趋势图,如图8 所示,相应的函数表达式可近似表示为

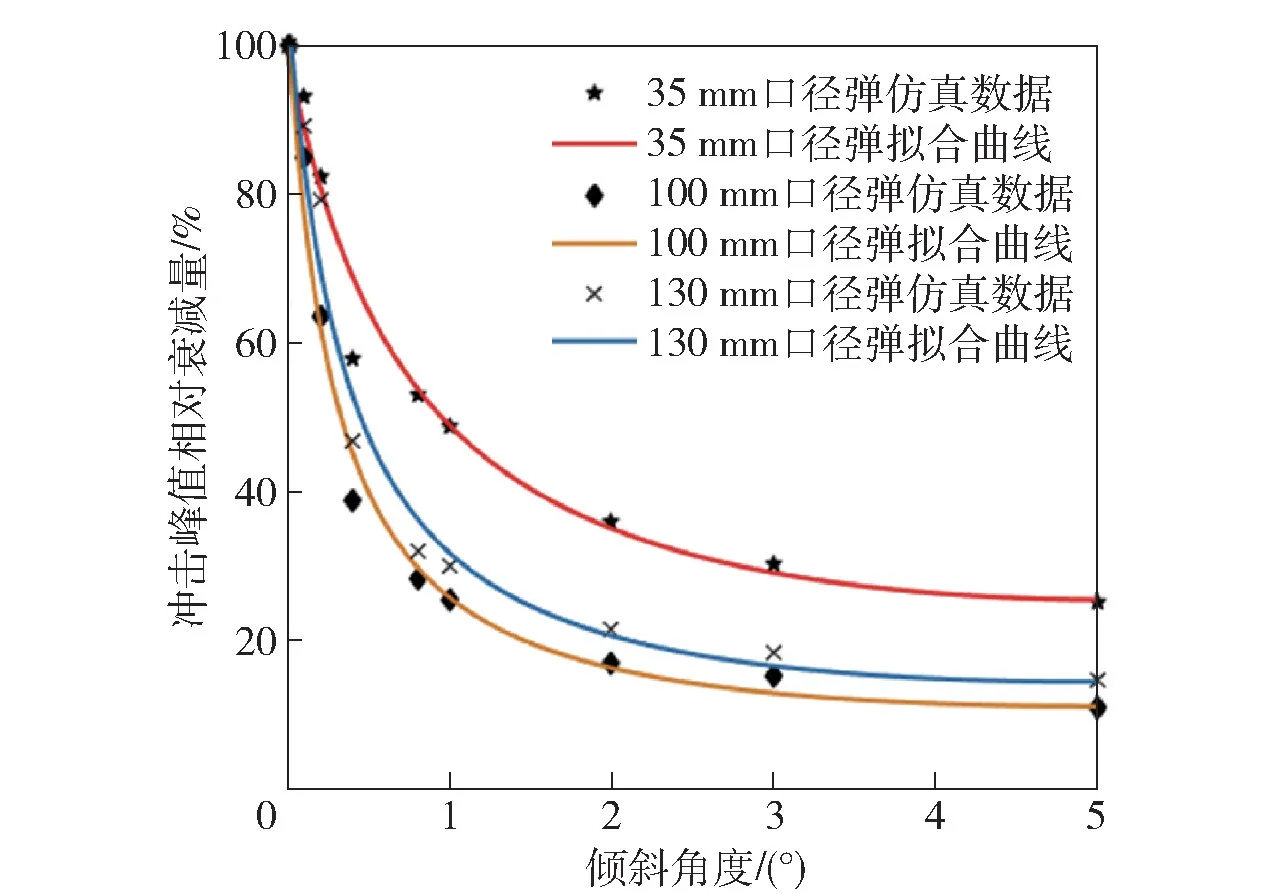
图8 引信跌落冲击峰值相对衰减量随倾斜角度的变化趋势Fig.8 Changing trend of relative attenuation of fuze drop impact peak with inclination angle

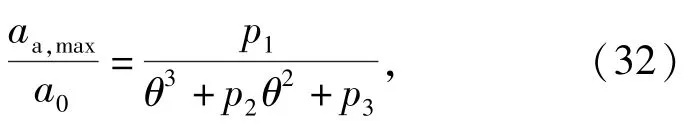
式中:为不同角度跌落下引信跌落冲击峰值;为垂直跌落时引信跌落冲击峰值;为弹丸倾斜角度;、、均为常系数。

6 种不同口径弹丸以不同角度从1.5 m 高度跌落至钢板,其弹丸跌落冲击加速度峰值仿真结果如表16 所示。弹丸倾斜角度对跌落冲击峰值影响是巨大的,考虑到传统自由落体式跌落试验弹丸跌落姿态接近“随机”,且样本量很少,实际测试结果难以出现完全垂直跌落的极端情况,因而所得加速度峰值会系统变小而作用时间会系统变长,故由此可认为本文推导的弹丸跌落产生的冲击加速度峰值和冲击作用时间计算公式具有较高的可信性。

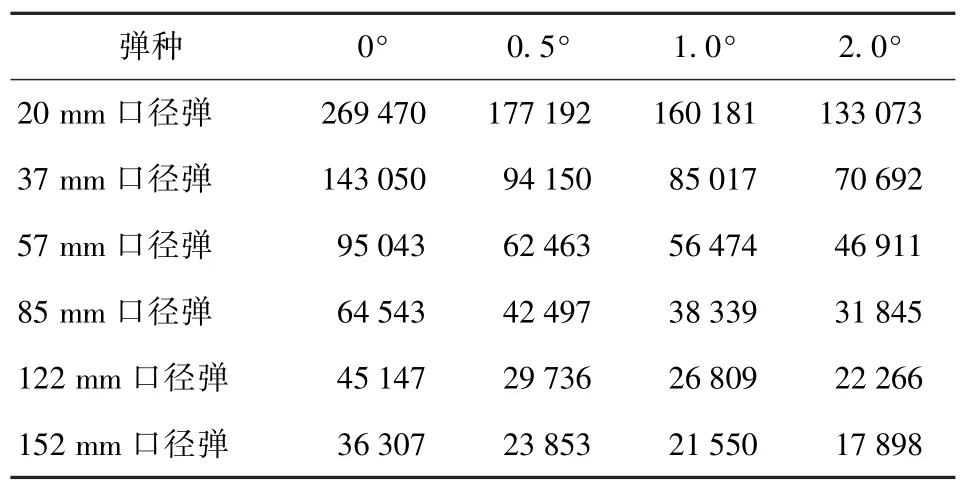
表16 不同口径弹丸以不同角度从1.5 m 高度跌落于钢板时的弹丸冲击加速度峰值Tab.16 Peak impact acceleration of projectiles with different calibers dropping on steel targets from 1.5 m height at different angles g

4 结论

本文采用弹塑性力学理论推导出了底部为圆柱形的弹丸垂直跌落碰撞地面目标过程的冲击加速度峰值和作用时间理论计算公式;利用有限元软件对不同口径缩比弹丸进行了跌落数值仿真,对冲击加速度峰值和作用时间的仿真结果进行了常系数修正,得到了裸态平底榴弹弹丸底向下垂直跌落时弹丸和引信的冲击特性公式。得到主要结论如下:

1) 弹丸直径越大,跌落时产生的冲击峰值越小,冲击作用时间越长;跌落高度仅改变冲击加速度峰值大小;碰撞恢复系数仅改变冲击作用时间的长短。

2) 在完全弹性碰撞的情况下,弹丸以同一高度跌落至任意目标,冲击加速度峰值与冲击作用时间乘积是恒定不变的。