自动驾驶中量子认知与决策问题研究
宋清源 傅卫平 王 雯 高志强周劲草郝大鹏
(1.西安理工大学机械与精密仪器工程学院,陕西西安 710048;2.西安外事学院工学院,陕西西安 710077;3.西安航空学院理学院,陕西西安 710077)
1 引言
自动驾驶汽车代替人类驾驶汽车出行将成为未来的必然趋势;同时,在相当长时期内,自动驾驶汽车将与人类交通参与者(包括行人和人工驾驶的各种机动与非机动车辆)共享城市道路.为了在城市复杂混合交通环境中安全高效行驶,自动驾驶车辆需要正确估计人类交通参与者的行为意图,并像人类驾驶车辆那样与人类交通参与者自然地相互作用[1-2].否则,面对交通参与者不遵守交通规则的场景,自动驾驶汽车是寸步难行的[3].人类交通参与者的行为及其相互作用在现实世界中往往具有明显的不确定性和非理性,而自动驾驶的“长尾”问题与非理性的行为意图和不确定的相互作用有关[4],需要采用正确而有效的认知与决策理论进行研究.但是,目前尚缺少有关研究人类交通参与者非理性行为的有效方法.
交叉路口是典型的交通参与者相互作用场景.自动驾驶车辆在无右转指示灯的交叉口即将右转时,会与非机动车道的其他交通参与者发生交互行为.目前,对人类交通参与者的认知与决策行为研究多基于完全理性的和相互独立的假设[5],并且均采用基于经典概率的认知与决策理论进行研究,然而,已有人类行为认知与决策理论的研究结果表明,人类的行为与经典认知与决策理论中的完全理性假设是不相容的[6],基于经典概率的认知与决策理论不能准确地描述人类的行为及其相互作用,这使得自主驾驶系统不能有效处理其他交通参与者的非理性行为以及相互作用等固有的不确定性,因而成为影响自主车辆安全运行的主要瓶颈之一.而量子理论为研究人类交通参与者不确定性行为(包括非理性行为)及其相互作用提供了一种新途径.
2 研究现状
2.1 人类交通参与者行为意图识别
学者们将人类交通参与者的人体特征、为动作作为意图估计的依据,研究者们进行了大量利用人体特征进行行为预测的研究.Koehler等人[7]使用行人运动的轮廓推断行人过街的意图.该轮廓线的主要特征是行人身体弯曲程度和腿部伸展程度;Kooij等人[8]借助头部朝向特征估计行人意图,他们认为,当行人面朝接近车辆时,行人更有可能在过街之前与车辆进行协商;Fang等人[9]使用了单目视觉二维姿态估计方法预测行人和骑自行车人的过街行为,经典概率模型不适用于真实场景.这使得上述方法有一定局限性.更多的学者开始利用基于经典概率模型的机器学习去估计行人意图.Markus等人[10]将部分可见马尔科夫(partially observable Markov decision process,POMDP)模型与紧急制动系统结合,用POMDP预测行人发生碰撞的概率,减少不必要的制动;Jos等人[11]用增长的隐马尔科夫模型(grow hidden Markov models,GHMMs)从在线数据中学习,无需人工干预.实验表明在基于社会力的运动模型中利用GHMM估计的人的预期位置,与基于标准恒速模型相比,可以获得显著的性能提高,Wu等人[12]提出了一种基于马尔科夫模型(Markov decision process,MDP)的概率方法来预测城市环境中的行人运动,Koehler等人[13]等人提出常用的解决复杂环境中行人意图估计问题的方法是动态贝叶斯网络(dynamic Bayes network,DBN),它从概率图形模型中继承了各种建模方案和大量精确和近似推理和学习技术,Kooij等人[8]提出采用DBN和切换线性动力系统(switching linear dynamics system,SLDS)来推断下一个行人的运动,Rudenko等人[15]提出了一种用于行人预测的DBN,该DBN有两种运动模式(行走和站立).基于经典概率模型的机器学习对预估行人假设为完全理性,在实际环境中行人不一定按照既定的模式运动.
绝大多数研究仅把交通参与者看成是没有认知能力的运动物体,假设其行为是理性的.然而,已经有证据表明,对于人类的某些行为,特别是非理性行为,包括交通环境中的人类行为,往往偏离基于经典概率的行为理论预期[16],因而可能成为自动驾驶安全导航的潜在风险.
2.2 量子认知与决策理论
量子力学是上世纪最伟大的发现,极大地推动着现代科学技术的发展,成为了新兴科学技术的理论支柱.认知领域的学者发现,量子力学中干涉和纠缠与人类认知中的交互作用有很多相似的特点,这一发现促使量子力学的数学表达方法被构建,并将量子概率引入认知领域,尝试利用量子力学独有的特征建立认知模型,解释基于经典概率的认知决策理论无法解释的人类认知领域难题,建立在量子概率基础上的量子认知决策理论逐渐孕育而生[17],不仅形成了日臻成熟的理论体系,而且得到日益广泛的应用[2].特别是在与无人驾驶技术最密切相关的移动机器人领域初显的量子端倪[16],更让人们看到了应用量子理论解决自动驾驶认知与决策问题的潜力和可能性.量子理论为研究人类交通参与者不确定性行为(包括非理性行为)及其相互作用提供了一种新途径.量子概率与经典机器学习理论(MDP,POMDP,DBN,HMM等)结合产生的量子认知决策理论,为自动驾驶系统认知决策研究提供了更为先进且有效可行的理论工具.
综上所述,目前尚缺少考虑人类交通参与者非理性行为的自动驾驶认知与决策的系统性方法,虽然量子认知与决策理论近年来取得长足发展,为研究考虑人类交通参与者行为(包括非理性行为)和相互作用的自动驾驶认知与决策问题提供了新的方法,但是目前尚无应用于自动驾驶领域的研究案例.本文将量子认知理论与锚定效应相结合,以交叉路口自动驾驶汽车右转与非机动车道上的交通参与者发生交互为背景,分析自动驾驶车辆右转时非机动车辆和行人的行为意图及其演化规律,建立量子决策模型,为自动驾驶车辆行驶提供策略依据.
3 研究模型构建
3.1 构建场景
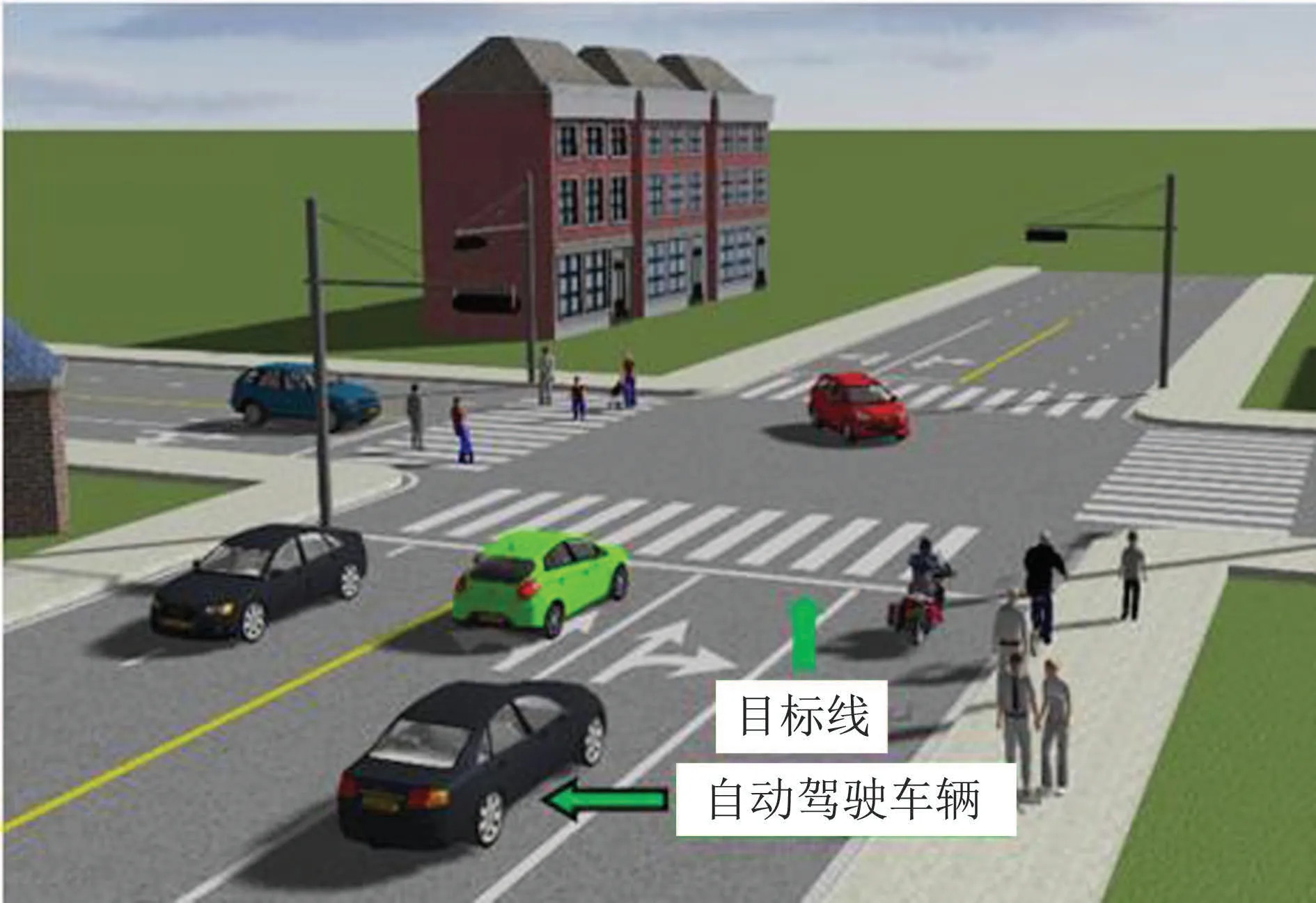
如图1所示,自主车即将右转,在临近交叉口处观察到非机动车和行人,但对行人或非机动车的未来状态(直行、左转或右转)未知.可分情况讨论:1)若行人或非机动车右转,则行人或非机动车占内侧道路,自主车占外侧道路,不发生交互行为,可以忽略;2)若行人或非机动车直行或者左转,都会与自主车发生交互行为,行人或非机动车可能会在行进过程中发生不确定性或非理性行为,比较典型且经常发生的行为如行人或非机动车不遵守交通规则.行人突然接打电话.非机动车由于路滑翻车等,这些行为都会影响到交互结果(发生碰撞或安全通过).
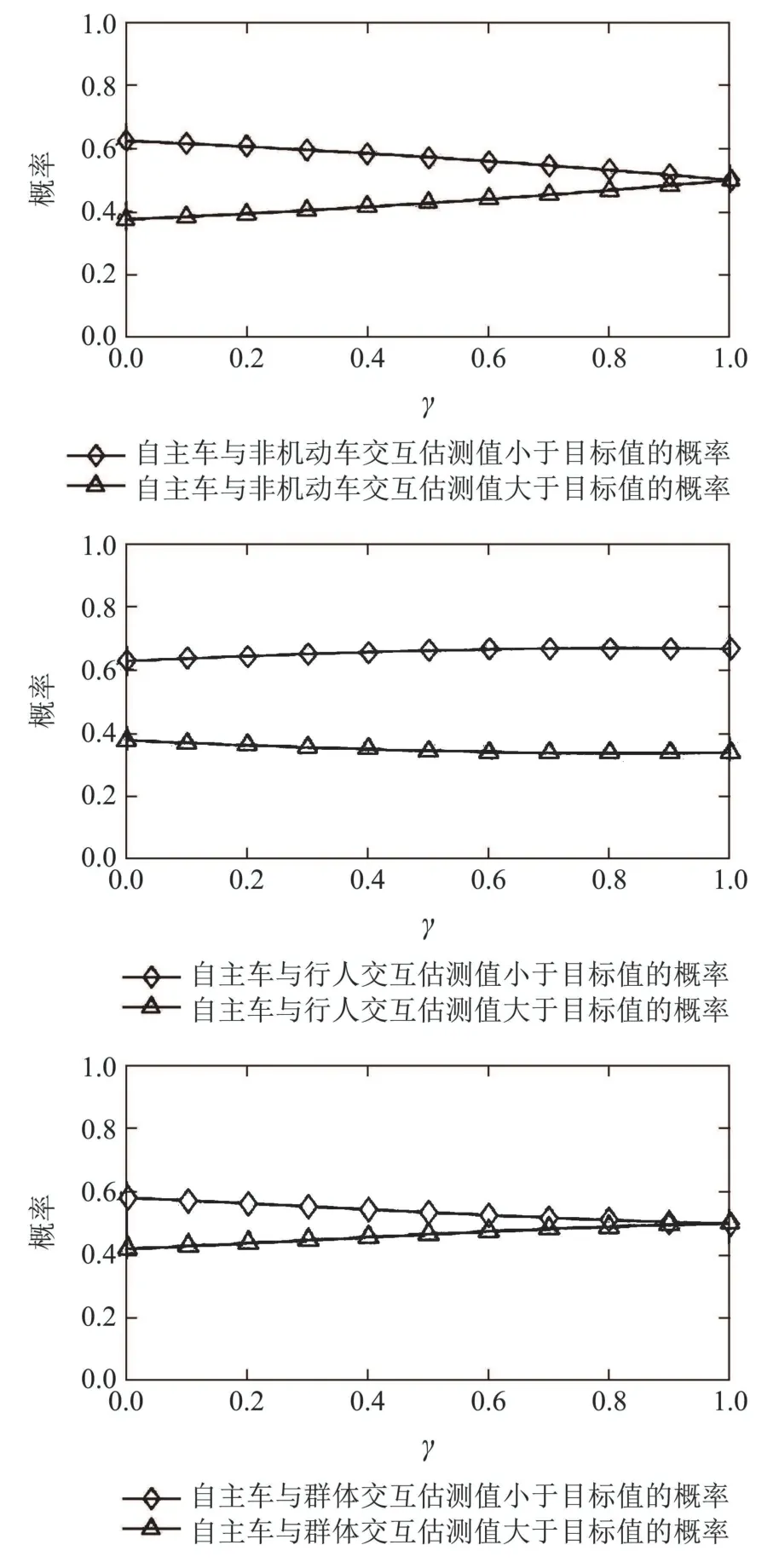
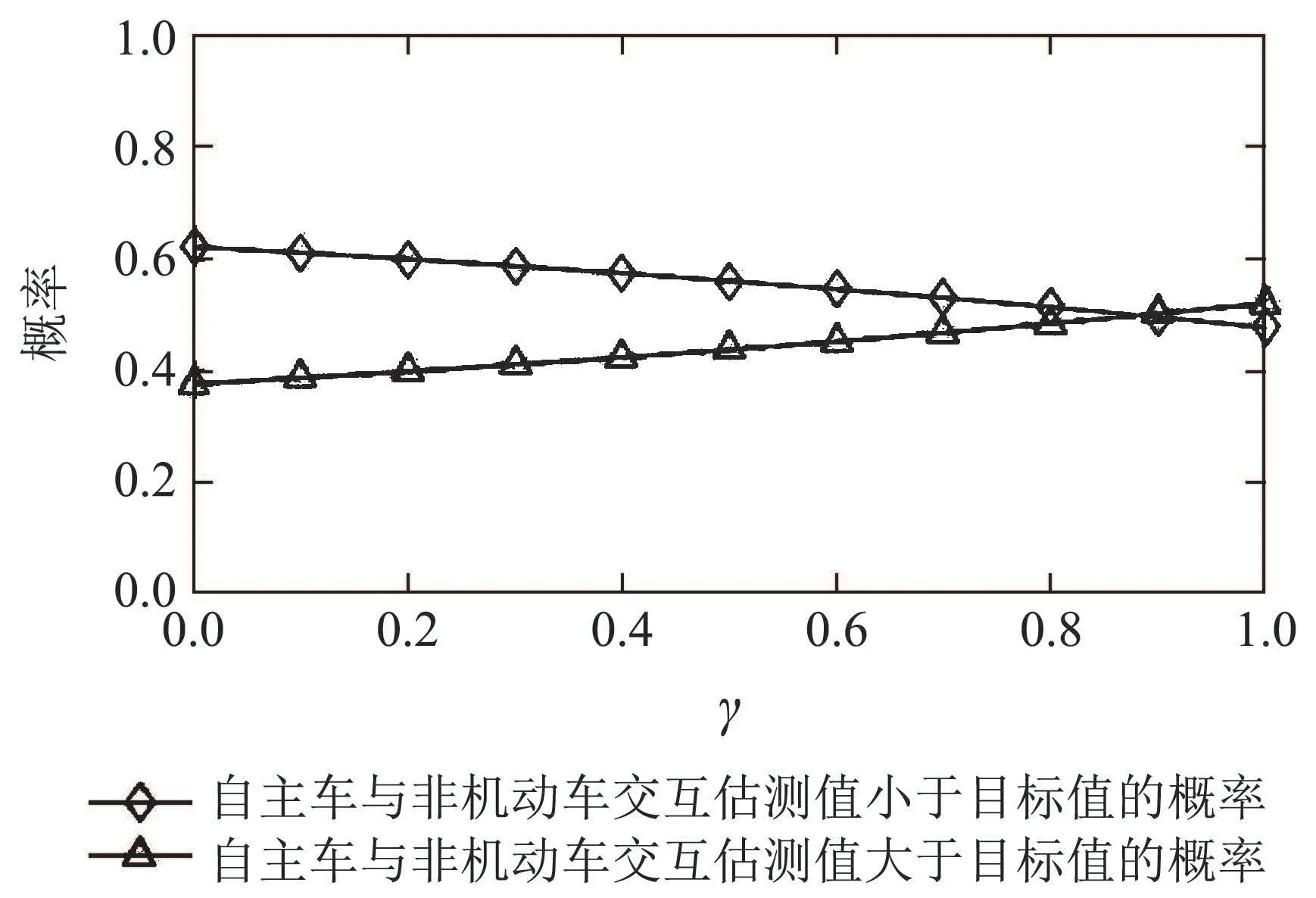
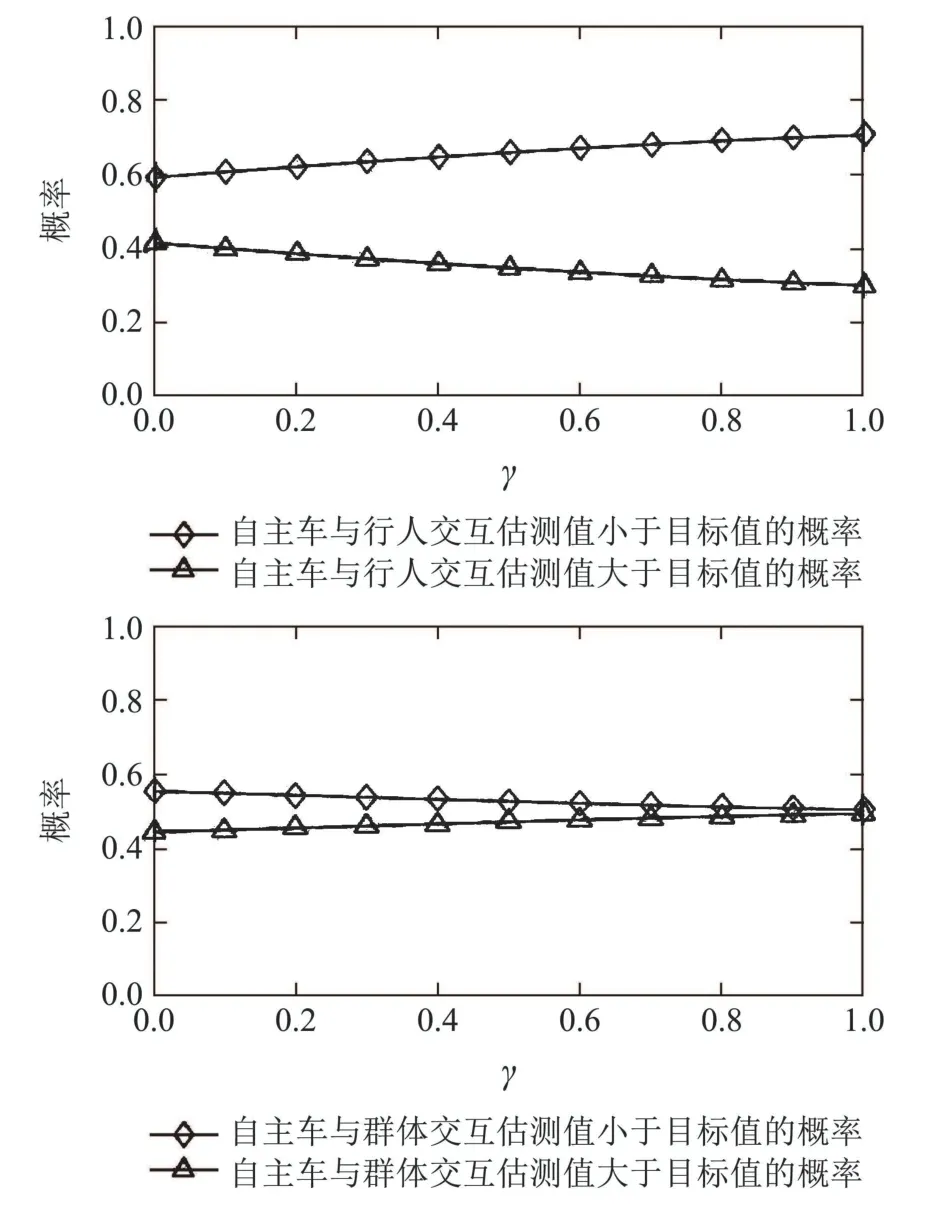
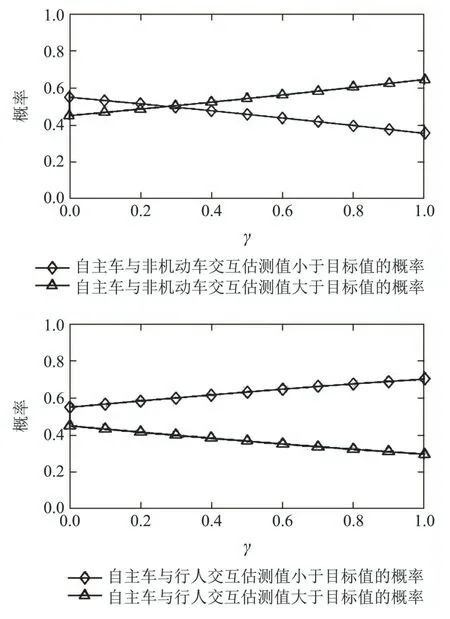
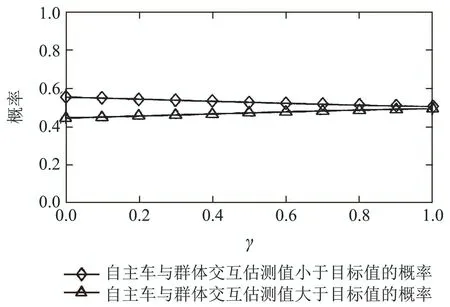
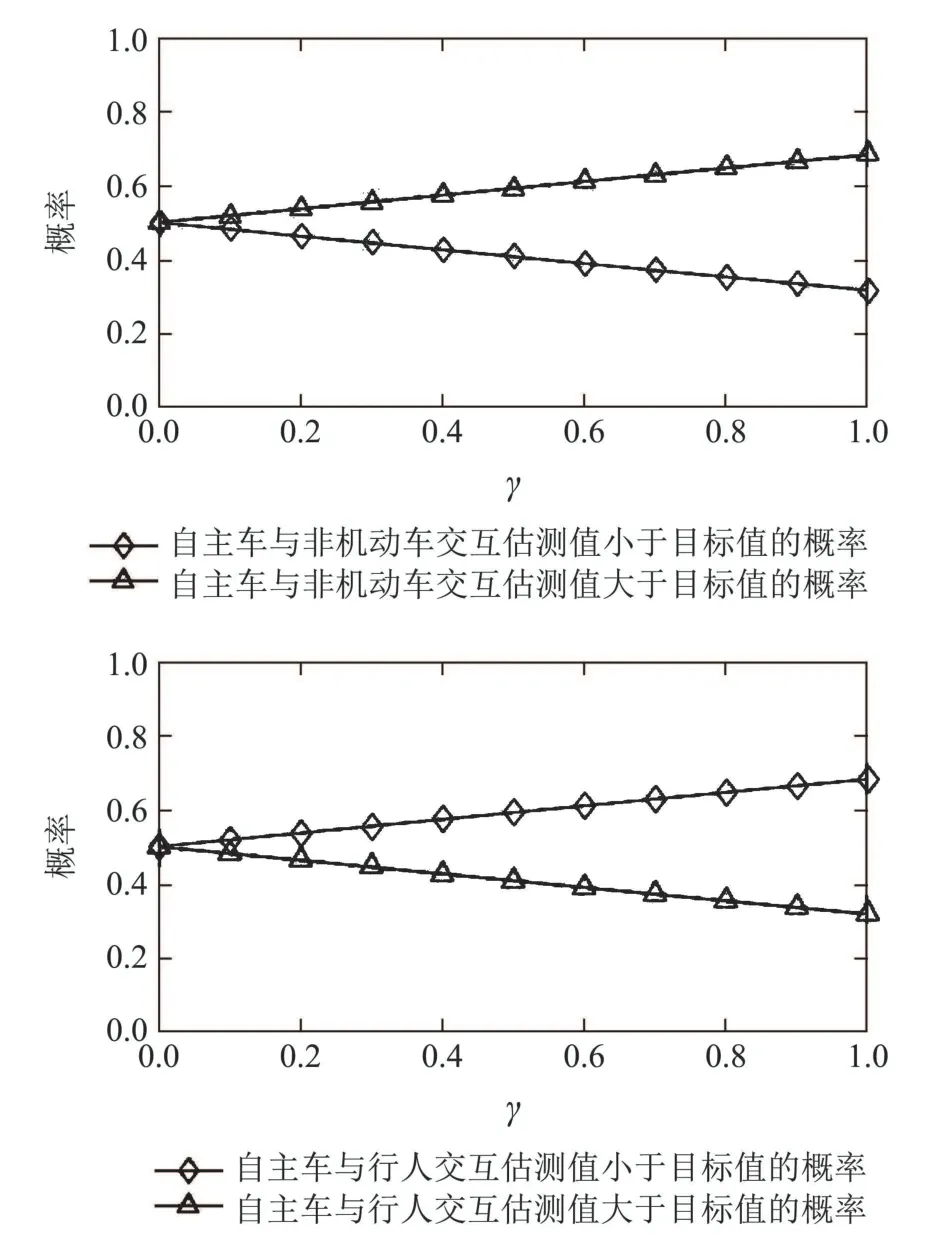
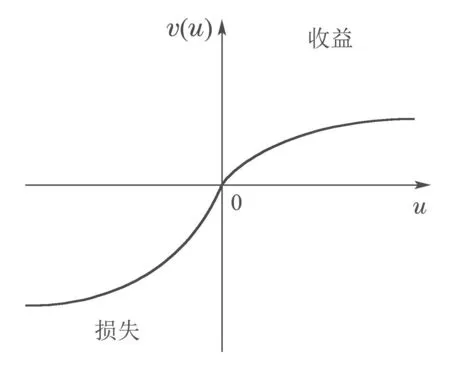
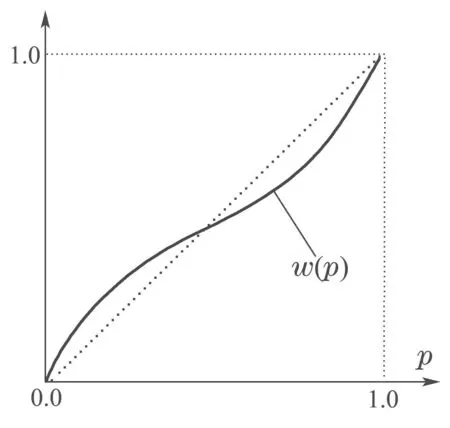
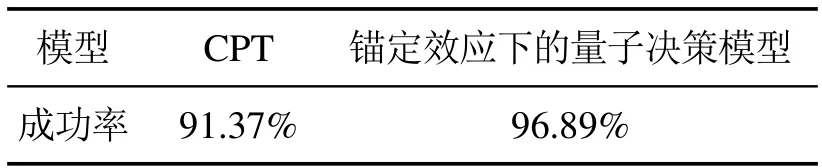
在自主车与行人或非机动车发生交互之前,将真实交通场景中的停车线(图中标注目标线)作为目标,设自主车从当前位置到目标线的时间为T1,行人或者非机动车从当前位置到目标线的时间为T2,比较T1与T2的大小,为自主车提前采取正确的决策提供了有效的策略依据.特别需要说明的是,自主车将T1设置为交互时的参照时间,设定T1为估测值,将T2设定为实际值,若T1 根据以上分析,在能够考虑到行人或非机动车的不确定因素和非理性行为的情况下正确判断T1与T2的大小,能够在真实路况中,做出正确且符合实际情况的决策,是本次研究的重点. 所谓锚定效应(anchoring effect)是指当人们需要对某个事件做定量估测时,会将某些特定数值作为目标值,目标值像锚一样制约着估测值.在做决策的时候,会不自觉地给予最初获得的信息过多的重视[18]. 根据第3.1节所设定的场景,图1中不论自主车还是非机动车或行人,过了目标线之后便是冲突交互区域,将自主车当前位置至目标线位置的时间t1设定为目标值,将自主车预估非机动车/行人到达目标线位置的时间t2/t3分别设定为估测值,通过量子认知模型结合锚定效应,准确判定t1与t2/t3的大小,从而帮助自主车做出加速通过或减速让行的决策. 图1 自动驾驶车辆右转与非机动车和行人交互场景Fig.1 The scene of autonomous vehicle turning right with nonmotor vehicle and pedestrians interaction 本文将自主车观测到目标线时还未到目标线的非机动车和行人定义为处于锚定条件,自主车未观测到目标线时非机动车和行人定义为没有处于锚定条件.在没有处于锚定条件时,有两种相互排斥且完全包含所有情形组成的集合,即估测值低于和高于标准值,集合内的元素用量子态的形式表示成{|L>,|H >},其中:|L>表示估测值低于目标值,|H >表示估测值高于目标值.最终测量时的状态可以写成两者的叠加态,即|ψ>=α|L>+β|H>,其中α和β均为复数,且满足归一化条件|α|2+|β|2=1.据量子波幅性质,估测值低于目标值的概率为α,而高于目标值的概率为β. 处于锚定条件时,可以用集合{|LL>,|LH >,|HL>,|HH >}来表示所有可能的情况,其中第1个字母表示所处于的锚定条件,L表示低锚定条件,在同等条件下由于非机动车到达目标线时间比行人用时少,故本文中的低锚定条件表示自主车与非机动车交互;同理,H表示高锚定条件,在本文中表示自主车与行人交互;第2个字母表示估测值和目标值相比,L表示比目标值低,H表示比目标值高.所以此时可以用函数来表示: 式中:M表示从未进入锚定条件到进入锚定条件的过渡矩阵;ψL表示自主车还没有进入锚定条件时,非机动车或行人到达目标线位置的时间(估测值)低于自主车从当前位置到目标线位置的时间(目标值)的概率波幅函数,同理,ψH与之类似;ψLL表示在低锚定条件下即自主车与非机动车交互时,估测值比目标值低的概率波幅函数,其他与之类似. 当自主车进入锚定条件进行比较估测值与目标值时,自主车的信念行为状态会依据收益矩阵动态地从初始状态ψ(0)转变为最终状态ψ(t),这一过程可以用薛定谔方程(式2)的解(式3)描述: 设矩阵U(t)=e−itHA为酉矩阵(unitary matrix),其中第i行第j列元素的模的平方|Uij(t)|2表示在时间t内从状态j转变为状态i的概率.该矩阵满足U†U=I,以保证状态ψ的内积不变,从而确保决策者在决策时转变为所有可能基态概率之和保持为I[17].在薛定谔方程中,哈密顿矩阵HA起着关键作用,在上述模型中,哈密顿矩阵仅根据决策者自身的收益矩阵建立,如下: 其中: 式中:uL,uH分别表示自主车判定估测值比目标值低、估测值比目标值高的效用函数,在本文中uL=uH=u,取值范围为u ∈[0,1].特别要说明的是,自主车在行驶过程中始终观察前方的路况,数值越趋向1,代表估测值与目标值越接近. 在此基础上,考虑到环境的不确定因素和非机动车或行人的非理性行为,加入“认知失调”矩阵[17],“认知失调”矩阵表示的是出现不确定因素和非理性行为时,行为随信念发生改变的关系: 上式建立的意义是:当自主车将要做出估计值比目标值低或者高的决策时(行为),第1个/第2个矩阵分别将参与决策的低锚定条件/高锚定条件考虑进去(信念).特别要说明的是 式中:γ表示信念与行为的纠缠的参数,其值越大,表示在相同时间内,这种纠缠的程度越大,取值范围为γ ∈[0,1].若γ >0那么第1行和最后1行的增长速度要大于中间行,所以,信念和行为一致的状态的振幅会增加. 式(4)-(5)本身不足以描述自主车与非机动车和行人交互的行为,因为它无法解释偏好如何随回报而变化.将式(4)-(5)结合后得到HC=HA+HB.因此,初始状态到最终状态的时间演化既反映了收益的影响,也反映了“认知失调”的过程. 在MATLAB平台上进行仿真计算,分为3种情况:1)自主车估测非机动车到达目标线的时间(估测值)与自主车到达目标线的时间(目标值)偏差概率分布;2)自主车估测行人到达目标线的时间(估测值)与自主车到达目标线的时间(目标值)偏差概率分布;3)自主车估测非机动车和行人组成的群体(以下简称群体)到达目标线的时间(估测值)与自主车到达目标线的时间(目标值)偏差概率分布. 计算以上3种情况时需要对初始函数ψ(0)进行设定,在估测非机动车到达目标线时间时,由于此时行人到达目标线的时间暂不考虑,所以ψHL和ψHH均为0;同理,在估测行人到达目标线时间时,ψLL和ψLH均为0;在估计群体到达目标线时间时,对各个概率波幅函数平均分配.特别需要注意的是,量子的概率振幅是模平方的形式,且满足归一性:ψ(0)表示如下: 式中ψ1(0),ψ2(0),ψ0(0)分别表示自主车估测非机动车、行人、群体到达目标线的时间这一过程的初始函数. 与锚定效应结合的新量子决策模型在计算自主车与非机动车交互时估测值比目标值低的概率分布时,除了要考虑自主车观测到的非机动车的状态之外,还要将可能出现的行人的状态考虑进去,最终的结果是ψLL和ψHL的和的概率振幅.计算自主车与行人或群体交互时与此同理. 随着信念与行为纠缠的参数γ(横坐标)从0到纠缠最大值1,代表在真实道路环境中自主车与其他交通参与者(非机动车和行人)交互时非机动车或行人出现的非理性行为从完全理性至非理性程度逐渐增大,如在完全理性下,非机动车或行人在到达路口时速度应逐渐降低,待观察清楚后再起步前进,但若实际情形是非机动车或行人出现非理性行为时,在达到路口过程中速度非但不降速反而越来越快,则其加速度越大可以理解为信念与行为纠缠的参数越接近1. 当效用函数分别为u=1,u=0.8,u=0.6,u=0.4,u=0.2及u=0时上述3种情况的概率分布(纵坐标),最终得到结果如图2-7所示. 图2 u=1时自主车分别估测非机动车(上)、行人(中)和群体(下)到达目标线的时间(估测值)与自主车到达目标线的时间(目标值)偏差概率分布Fig.2 When u=1,the autonomous vehicle respectively estimated the deviation probability distribution of the time(estimated value)of non-motor vehicle(up),pedestrian(middle) and group (down) to reach the target line and the time (target value) of autonomous vehicle to reach the target line 图3 u=0.8时自主车分别估测非机动车(上)、行人(中)和群体(下)到达目标线的时间(估测值)与自主车到达目标线的时间(目标值)偏差概率分布Fig.3 When u=0.8,the autonomous vehicle respectively estimated the deviation probability distribution of the time(estimated value)of non-motor vehicle(up),pedestrian(middle) and group (down) to reach the target line and the time (target value) of autonomous vehicle to reach the target line 图4 u=0.6时自主车分别估测非机动车(上)、行人(中)和群体(下)到达目标线的时间(估测值)与自主车到达目标线的时间(目标值)偏差概率分布Fig.4 When u=0.6,the autonomous vehicle respectively estimated the deviation probability distribution of the time(estimated value)of non-motor vehicle(up),pedestrian(middle) and group (down) to reach the target line and the time (target value) of autonomous vehicle to reach the target line 图5 u=0.4时自主车分别估测非机动车(上)、行人(中)和群体(下)到达目标线的时间(估测值)与自主车到达目标线的时间(目标值)偏差概率分布Fig.5 When u=0.4,the autonomous vehicle respectively estimated the deviation probability distribution of the time(estimated value)of non-motor vehicle(up),pedestrian(middle) and group (down) to reach the target line and the time (target value) of autonomous vehicle to reach the target line 图6 u=0.2时自主车分别估测非机动车(上)、行人(中)和群体(下)到达目标线的时间(估测值)与自主车到达目标线的时间(目标值)偏差概率分布Fig.6 When u=0.2,the autonomous vehicle respectively estimated the deviation probability distribution of the time(estimated value)of non-motor vehicle(up),pedestrian(middle) and group (down) to reach the target line and the time (target value) of autonomous vehicle to reach the target line 图7 u=0时自主车分别估测非机动车(上)、行人(中)和群体(下)到达目标线的时间(估测值)与自主车到达目标线的时间(目标值)偏差概率分布Fig.7 When u=0,the autonomous vehicle respectively estimated the deviation probability distribution of the time(estimated value)of non-motor vehicle(up),pedestrian(middle) and group (down) to reach the target line and the time (target value) of autonomous vehicle to reach the target line 在锚定效应下图2-7可以简化理解:带菱形线表示非机动车(上)、行人(中)和群体(下)先到目标线的概率,带三角形线表示自主车先到目标线的概率.前文所述,u越趋近于1,代表估测值与目标值越接近. 由图2-7可知,当u=1时,即估测值与目标值最接近时,自主车估测非机动车或者行人到达目标线的时间均小于自身到达目标线的时间,在信念与行为纠缠的参数γ最大时,群体与自主车同时到达目标线.此时自主车应该提前减速,等待非机动车和行人完全通过后再通过,避免交叉口处的拥堵. 当u=0.8,γ≥0.9时,自主车比非机动车先到达目标线,此时自主车应加速通过,行人和群体仍然比自主车先到达目标线,但其概率值与u=1时相比略有下降. 当u=0.6时,γ≥0.73时自主车比非机动车先到达目标线位置,其他与u=0.8类似. 当u=0.4时,γ≥0.52时自主车比非机动车先到达目标线位置,其他与u=0.8类似. 当u=0.2时,γ≥0.3时自主车比非机动车先达到目标线位置,其他与u=0.8类似. 当u=0时,即估测值与目标值相差最大时,自主车比非机动车先达到目标线位置,此时自主车应加速通过;行人在γ=0 时与自主车同时到达,随着γ增加,行人比自主车先到达目标线位置的概率更大,自主车应减速让行;群体与自主车到达目标线位置的时间顺序不再随着γ的增加而变化,会一直与自主车同时达到目标线位置,此时自主车应减速让行. 自动驾驶车辆需要正确估计人类交通参与者的不确定及非理性行为意图,并像人类驾驶车辆那样与人类交通参与者自然地相互作用.为了验证提出方法的有效性,将本文提出的锚定效应下的量子决策模型和累积前景理论模型(非理性行为评价方法)在同一个数据集中评价其实验表现情况.下面简要介绍累积前景理论模型. 累积前景理论(cumulative prospect theory,CPT)由Kahneman和Tversky[19]提出,它以一种统一的方式阐述了许多带有偏见或非理性的人类行为.与传统的预期效用理论(expected utility theory,EUT)相比,CPT在前景的定义中引入了两个额外的概念:1)P:定义在效用上的值函数V;2) 定义在累积概率上的决策权函数π.每个动作都由下列方程评估: 式中:函数V是严格递增函数,u+和u−分别为与参考效用u0相比,u的收益和损失.决策权重定义为 式中:w±是严格递增函数,通常,当u≥u0(增益)时,V(u)为凸函数,当u≤u0(损耗)时,V(u)为凹函数,且损耗比增益更陡峭.图8(上)显示了当u0=0被设置为参考效用时值函数的一个示例,许多实验研究表明,V和w的代表函数形式可以写成 图8 值函数(上图)和权函数(下图)的例子Fig.8 Examples of value and weight functions 式中:α,β,γ,θ ∈(0,1],λ≥1在图8(下)中,这种决策权重函数可以很好地描述人类倾向于高估低概率事件的发生而低估高概率事件的发生的观察到的行为. CPT模型假设决策者选择产生式(8)中定义的最大值的行为,即 实验数据集参考[20],选取无信号灯环形路口为交互地点,在该路口处非机动车、行人及群体出现频繁,如图9所示. 图9 数据集(无信号灯环形路口)中交互场景Fig.9 An interaction scenario in a dataset(a traffic roundabout without lights) 在此数据集中共搜集到283次目标车右转时与其他交通参与者交互场景,分别用锚定效应下的量子决策模型和累积前景理论模型(CPT)对其进行验证.锚定效应下的量子决策模型中假设信念与行为纠缠的参数γ随着交互处交通流密集程度线性增加,即交互处越拥堵γ越趋近1;CPT中设定{ap,ay}是判定目标车/其他交通参与者先到目标线时,目标车采取加速通过/减速让行的动作集,按照文献[21]中的方法将CPT中的参数通过逆强化学习(inverse reinforcement learning,IRL)的方式获得,假设U是由一些特征组成的线性组合,这些特征包括:速度、加速度、紧急制动和安全性. 将两种模型的验证结果在下表中展示,结果表明,锚定效应下的量子决策模型的决策正确率要高于累积前景理论模型,根据文献[21]的结果,锚定效应下的量子决策模型相比于神经网络模型结果接近且不需要大量数据驱动,这使得锚定效应下的量子决策模型数据效率更高. 从结果上看,锚定效应下的量子决策模型在自主车右转场景决策时更具有优势,主要原因有以下几点:1)CPT模型计算得到的概率值是基于经典概率计算得出的,并没有考虑到产生叠加态时的情况,如在设置动作集时,仅有加速通过和减速让车两个动作,而没有两者之间的状态,在实际场景中,很多交互车辆都会有犹豫不定的时候,故此方法并没有从根本上解决非理性的决策问题;2)在文献[21]中对CPT中的参数进行逆强化学习(IRL)时没有考虑到交互双方相互作用的影响,导致成功率相对较低;3)锚定效应下的量子决策模型相比于CPT模型考虑到了动作集合中的叠加态,舍弃掉完全理性假设,与实际情况更加相符. 表1 CPT模型与锚定效应下的量子决策模型成功率比较Table 1 Success rate comparison between CPT model and quantum decision model under anchoring effect 本文用量子理论与锚定效应相结合,构建出新量子决策模型,通过仿真和对比实验,证明了该模型能够在考虑到其他交通参与者存在非理性行为的情况下正确决策自动驾驶车辆右转行为,与非机动车、行人及群体交互时能够像人类驾驶员一样做出正确合理的决策,确保通行时的安全和高效. 在下一步的研究中,作者将应用更加复杂的交通场景,用量子理论进一步探索交通参与者之间的相互作用问题.帮助自动驾驶车辆能够更加清晰地分析真实的路况信息,促进自动驾驶车辆更加安全和高效.本文为自动驾驶场景中人类交通参与者有限理性行为的研究提供了参考框架.作者相信,随着量子认知与决策理论的进一步发展以及研究者们的不断探索,其在自动驾驶领域中的应用将更为广泛深入.3.2 锚定效应下的量子决策模型构建
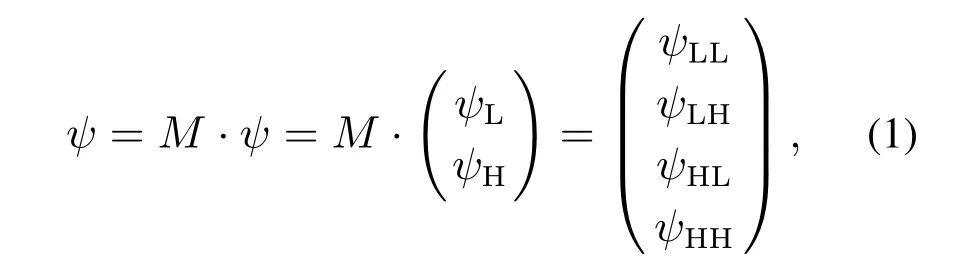
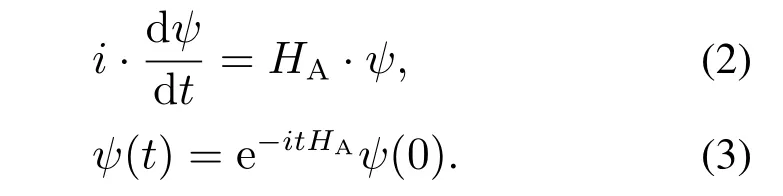
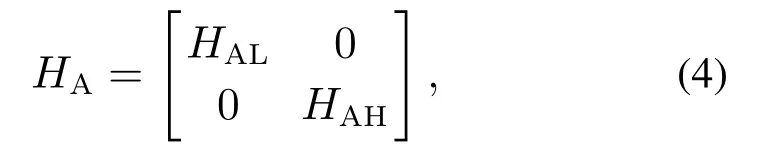
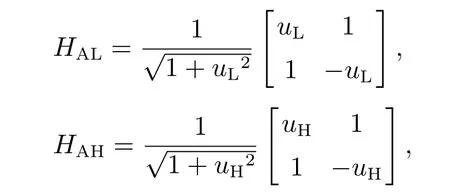


4 仿真分析
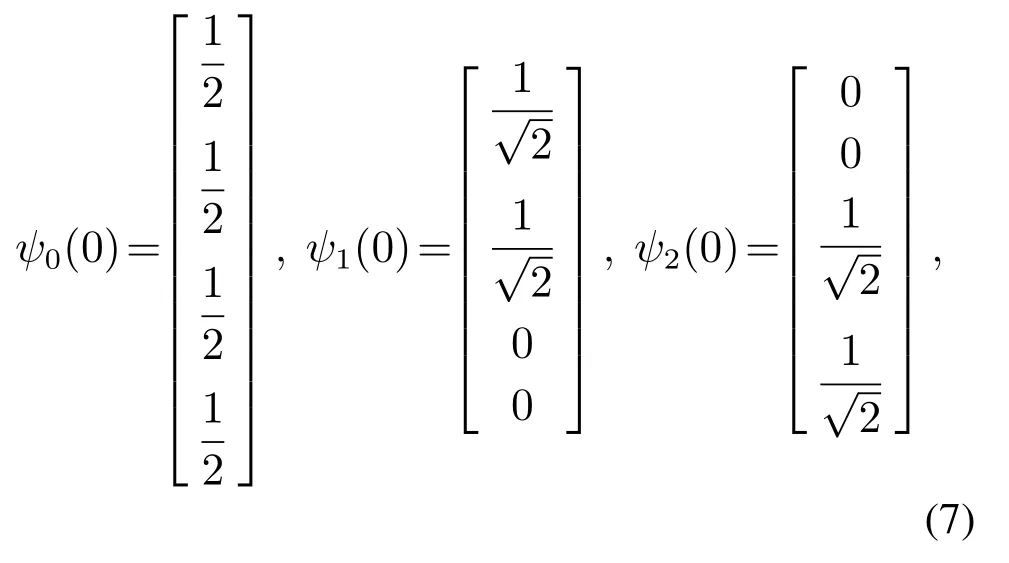
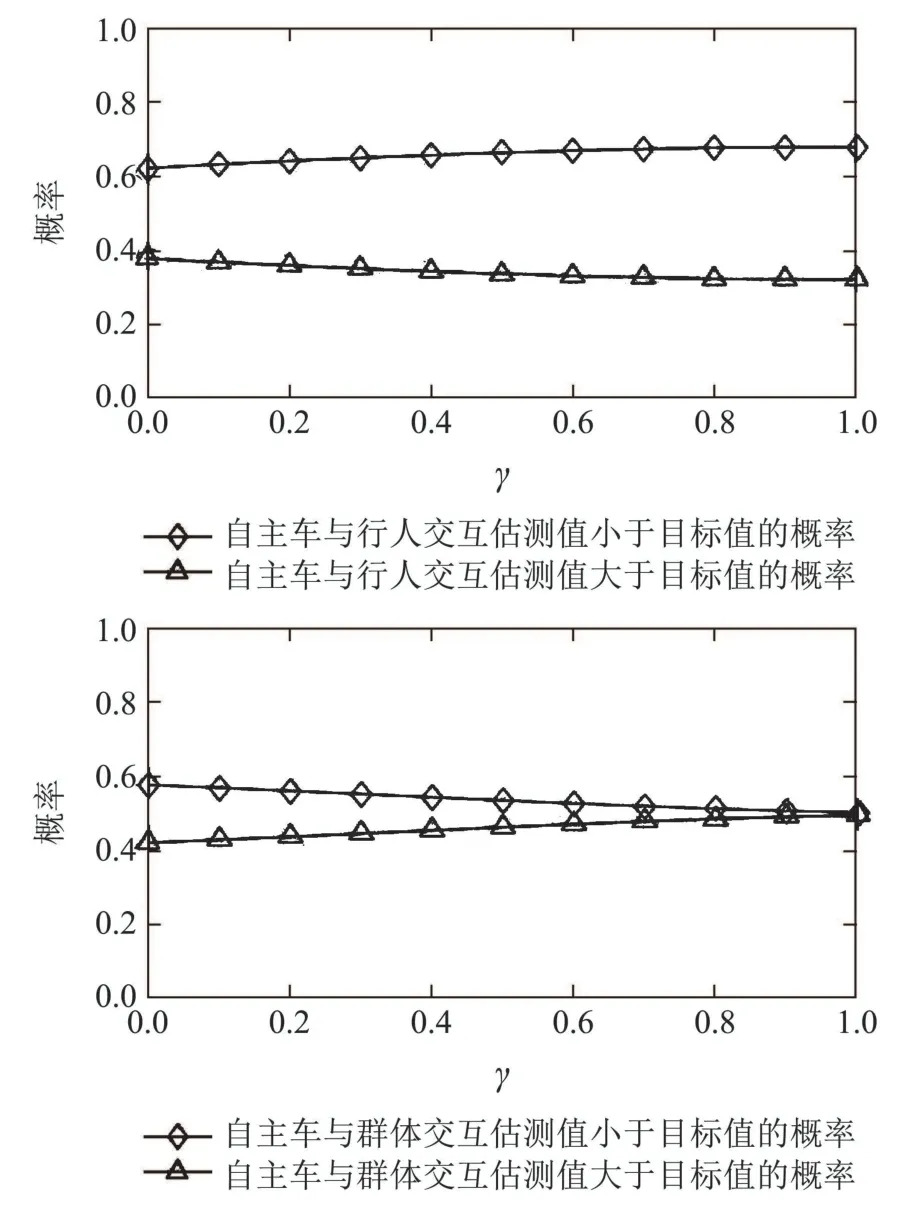
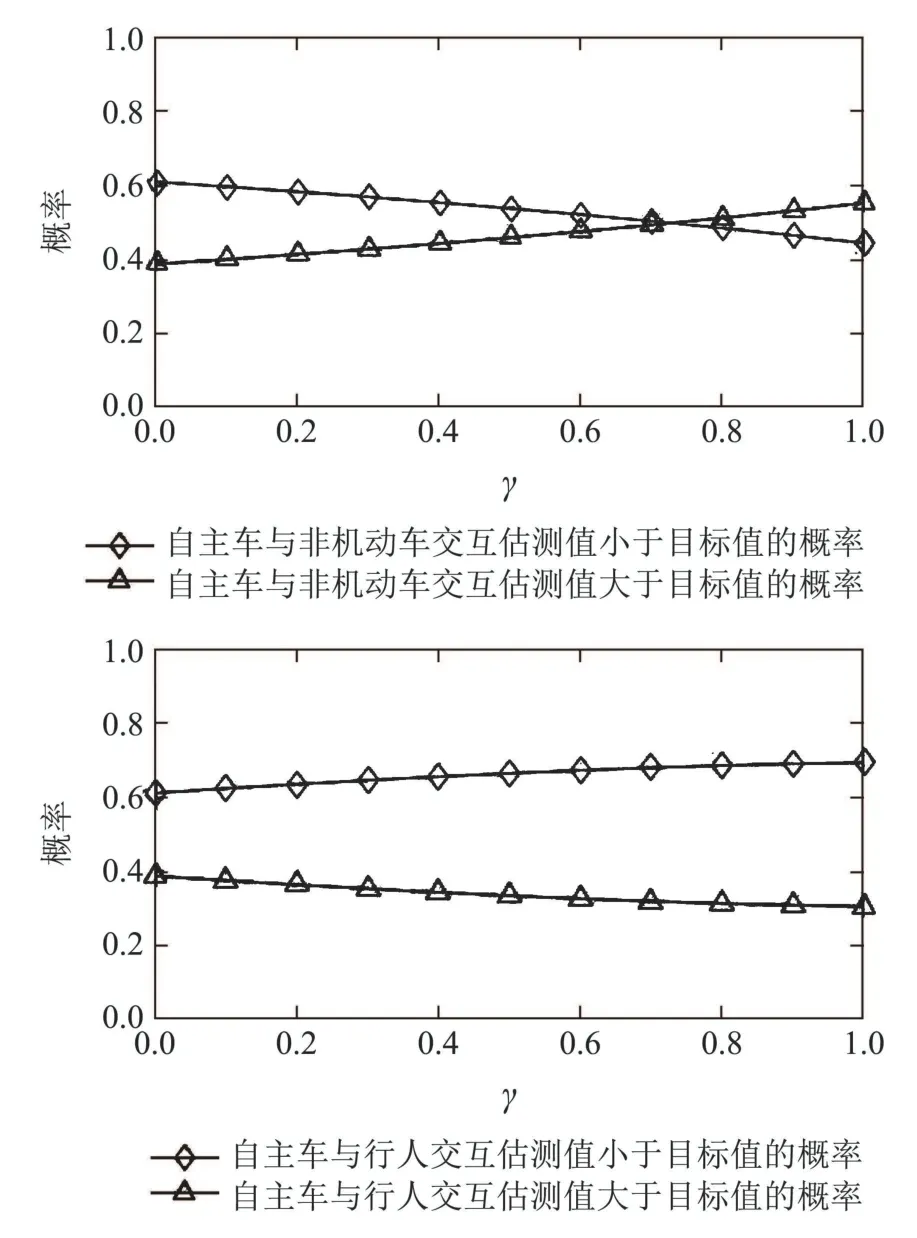
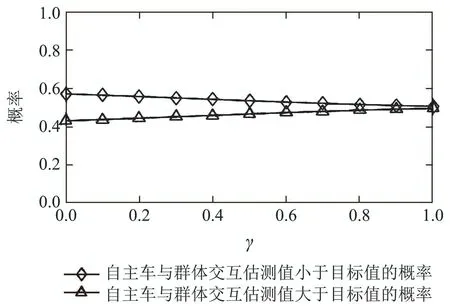
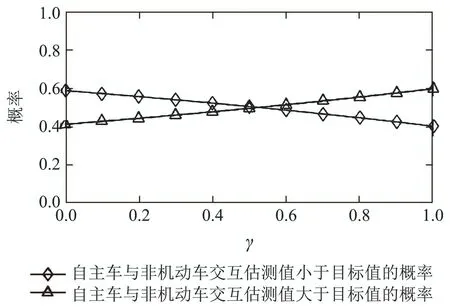
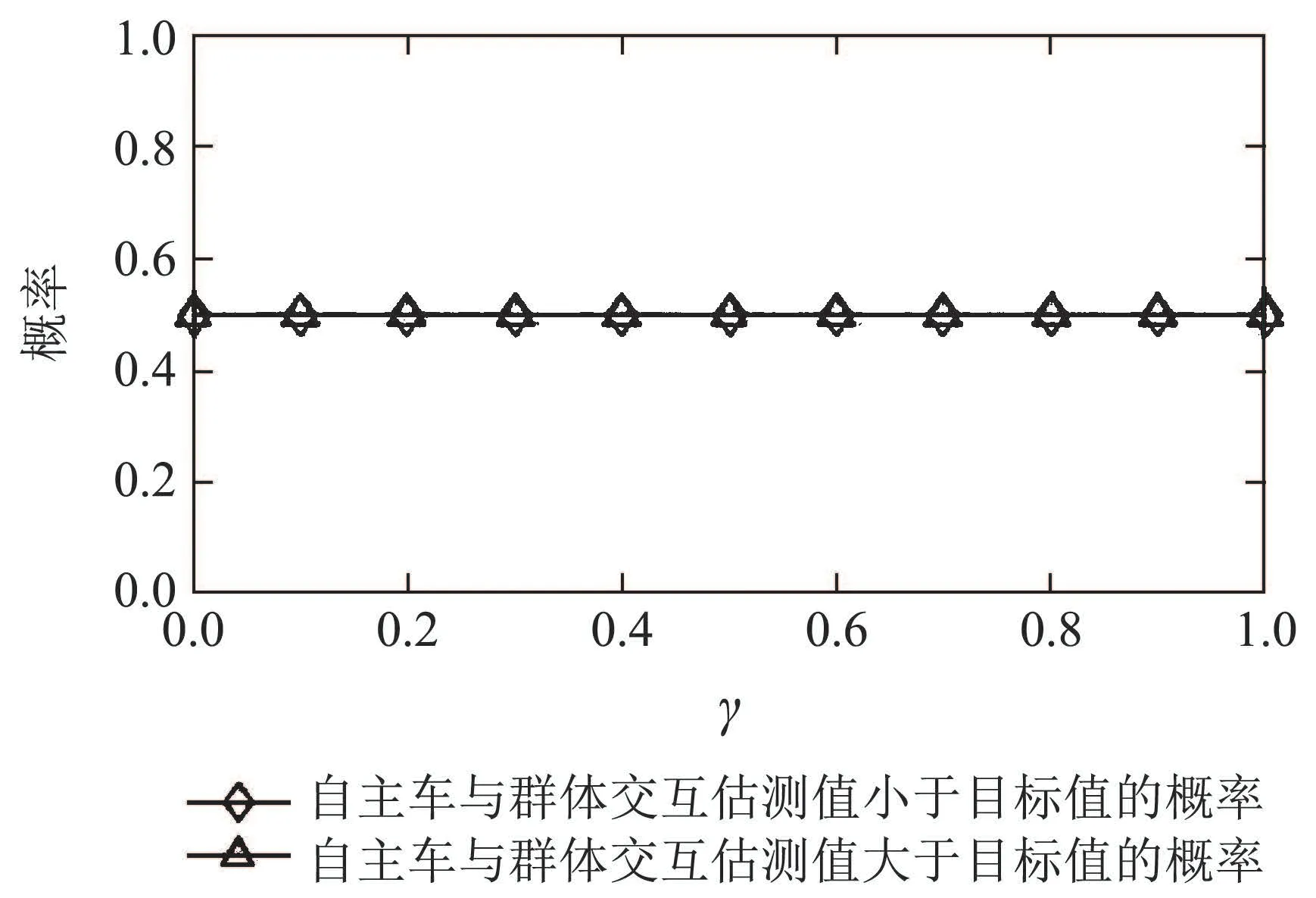
5 实验分析
5.1 累积前景理论模型(CPT)

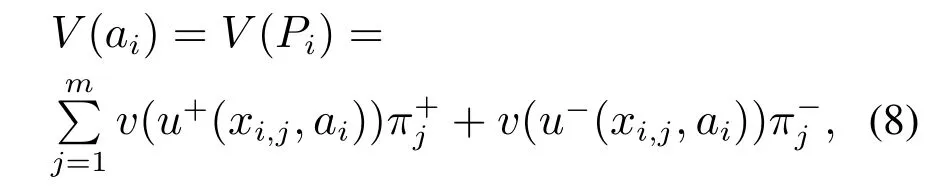
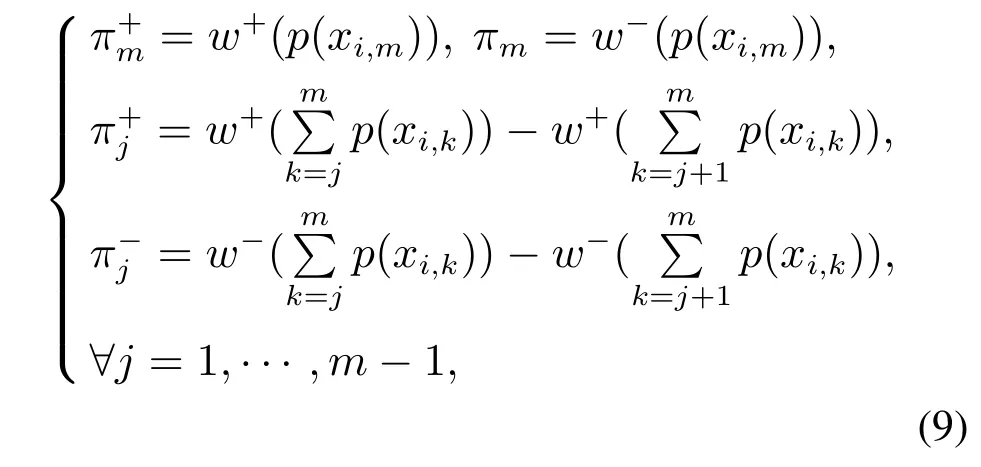
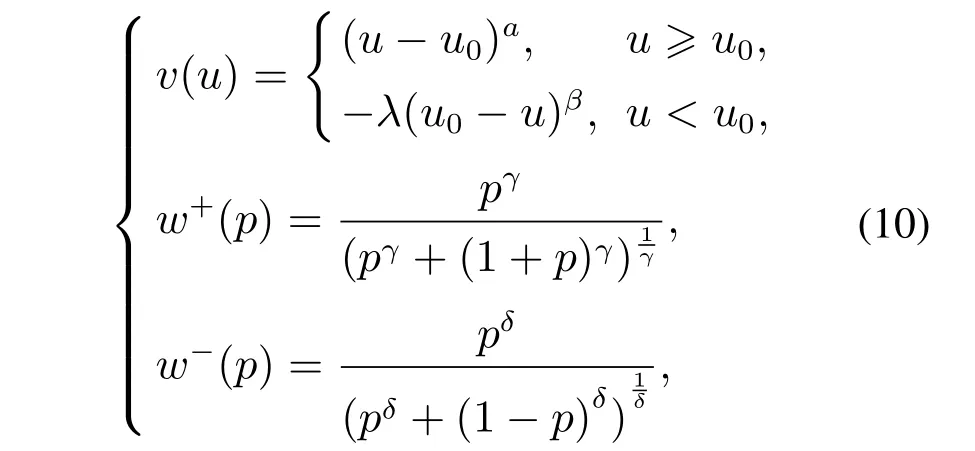
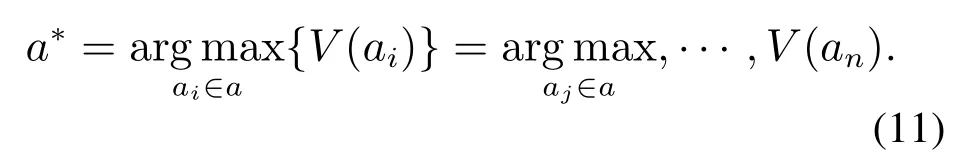
5.2 数据集

5.3 实验结果
6 总结及展望

