多目标约束下逆变器阻抗的电流矫正方法

杜 燕,言明明,杨向真,张梦梦,孙青青,苏建徽

(合肥工业大学电气与自动化工程学院,安徽合肥 230009;教育部光伏系统工程研究中心,安徽合肥 230009)

1 引言

随着分布式电源的广泛应用,大量变压器以及较长传输线路接入公共电网,使得电网逐渐表现出弱网特性[1].在弱电网下,并网逆变器的电流控制环[2-3]、锁相环(phase-locked loop,PLL)[4-5]均有可能和电网阻抗产生交互作用,且随着电网阻抗的增大,在短路比(short circuit ratio,SCR)小于5时,锁相环与电网阻抗间的耦合变强[6-7],低频谐波放大现象显著,导致系统失稳.这是由于PLL可等效为并联负阻抗[8-9],降低了逆变器输出阻抗在电网交互频段的相位,进而导致系统相位裕度降低.

对此,众多学者从重塑逆变器输出阻抗的角度,减弱、消除PLL对系统稳定性的影响.1)额外引入矫正环节:文献[10-11]从补偿系统相位裕度的角度出发,在并网逆变器控制环路并联虚拟阻抗,对逆变器输出阻抗进行重塑以达到改善系统稳定性的目标.2)对PLL特性重新整定:文献[8,12]利用相位裕度和SCR为约束设计PLL带宽,虽然提升了系统稳定性,但牺牲了电流动态跟踪性能.文献[13-14]在PLL支路上前置自适应积分滤波器、低通滤波器等多类型滤波器来改变PLL支路的阻抗特性,提高系统的弱网稳定性,但都需要添加相角补偿以弥补前置滤波器对基频相位造成的影响.

为了实现在保持PLL结构和带宽不变的条件下改善并网逆变器的弱网适应性的目标,本文提出了一种多目标约束的阻抗重塑法.基于等效变换的原则,在电流控制回路中增加电流二阶校正环节,并以基波跟踪性能、系统稳定裕度为约束优化设计了所提出的二阶校正环节参数,在不影响电流跟踪性能的前提下,提升了系统弱网下的稳定性.基于StarSim实验平台的实验结果验证了电流二阶校正方法和多目标约束优化方法的可行性和有效性.

2 基于阻抗模型的PLL影响分析

图1(a)为单相LCL并网逆变器系统结构框图,其中:Udc为直流输入电压;Vm为调制波;L1,C和L2构成LCL型滤波器;upcc(s)为并网电压,向PLL提供相位信息;并网电流ig(s)与滤波电容电流ic(s)的采样系数分别为Hi,Had;iref(s)为指令电流;Gc(s)为电流调节器.为实现基波电流的准确跟踪,本文采用准PR电流调节器,其传递函数为

式中:Kp为比例系数,Ki为谐振系数,ω0为基波角频率,ωc表示截止频率.

系统线性化后得到控制框图如图1(b)所示.图1(b)中,Kpwm表示PWM逆变环节增益,可近似为为三角载波幅值.本文采用单相系统中广泛应用的基于延迟的锁相环,其传递函数为[14]

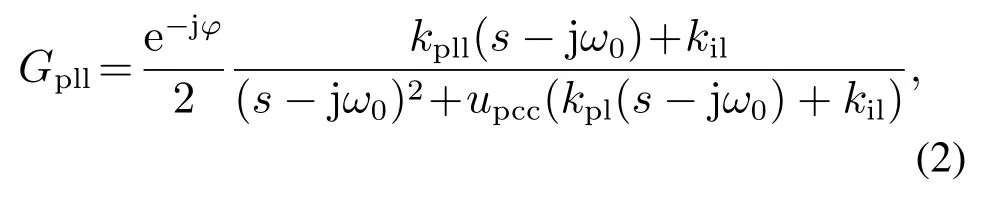
式中:kpl,kil为锁相环控制参数;ω0为基波角频率;φ是功率因数角,本文采用单位功率因数并网,故功率因数角φ=0.

根据阻抗建模,图1(a)系统可等效为Zout(s)与Zpll(s)并联模型[8],如图2所示.

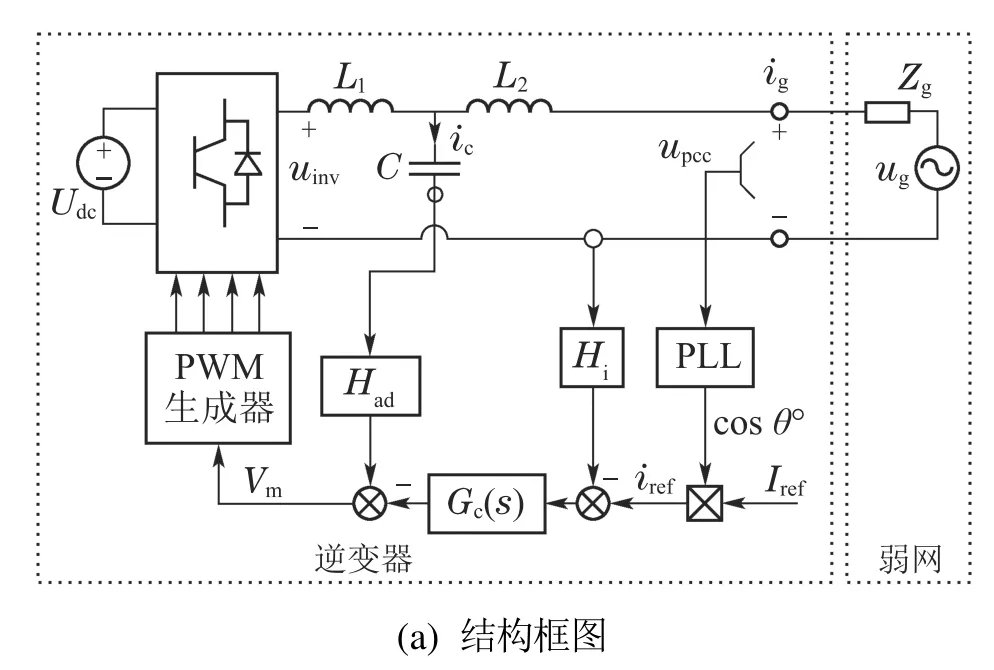
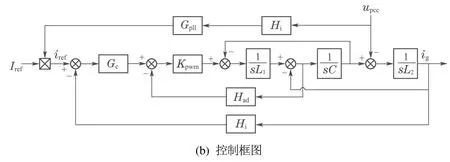
图1 LCL并网逆变器系统Fig.1 LCL grid-connected inverter system

图2 弱电网下并网系统等效电路Fig.2 Equivalent circuit of a grid-connected system in a weak grid

其中Zout(s)为不考虑PLL时逆变器的输出阻抗,Zpll(s)为PLL等效阻抗,其表达式分别为式(3)-(4),逆变器总的输出阻抗为式(5).

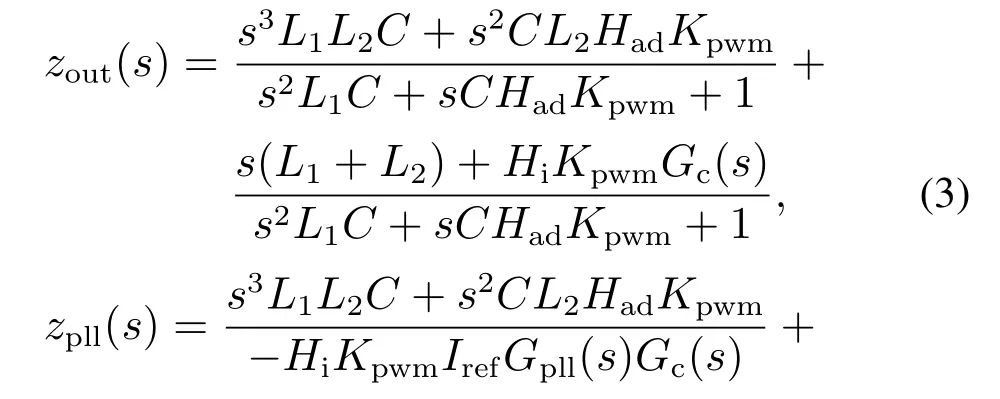
图3给出了Zout(s)和Zout−pll(s)Bode图,并网逆变器的系统参数如表1所示.

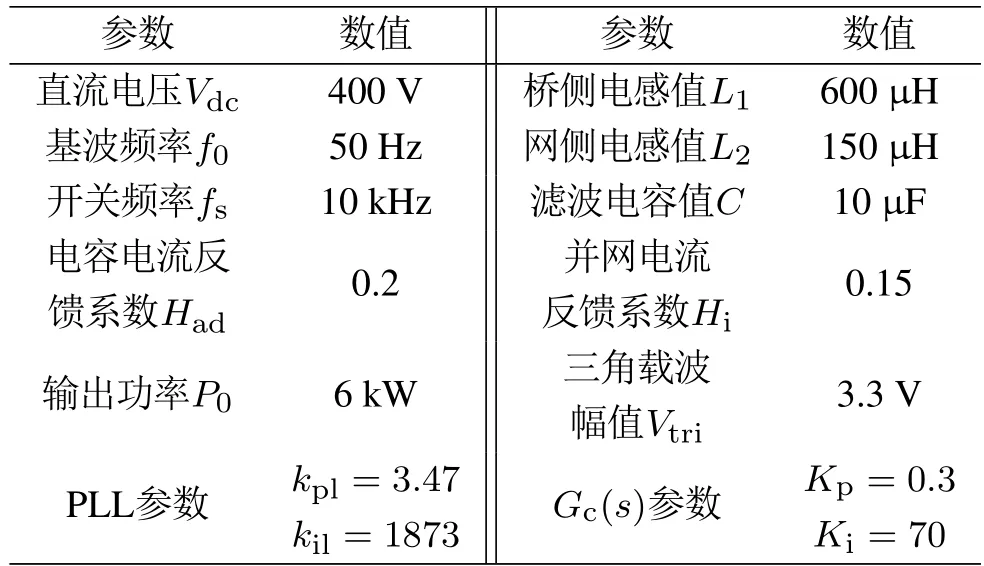
表1 单相并网逆变器参数Table 1 Single-phase grid-connected inverter parameters

由图3可以看出,锁相环在50 Hz以上频段会引入负阻特性[8],降低输出阻抗Zout(s)的相位,使得并联PLL后的输出阻抗Zout−pll(s)出现不稳定区段.因此,需在受PLL影响的频段对系统输出阻抗进行重塑,以减弱PLL的负阻特性.

图3 Zout(s)和Zout−pll(s)的bode图Fig.3 Phase-frequency responses of Zout(s)and Zout−pll(s)

3 基于电流二阶校正环节的输出抗重塑方法

低通滤波器(low pass filter,LPF)串入PLL可使其低频段衰减能力增强,有利于低频谐波的抑制,改善系统稳定性[9].加入LPF后的PLL控制框图如图4所示.

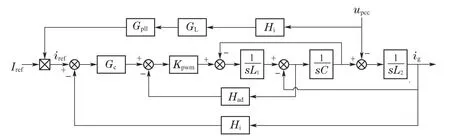
图4 PLL支路串联低通滤波器Fig.4 PLL branch series low-pass filter

添加LPF后逆变器输出阻抗为式(6),其中,GL(s)为LPF传递函数,表达式为

式(7)中:α为阻尼系数,ωh为LPF 的带宽,本文考虑SCR=2时的最恶劣工况,根据文献[9]所提设计方案选取ωh=416 rad/s,α=0.6.加入LPF后,Zout−pll−L(s)在基频处产生相位偏移现象,偏移量达|Δφ1|=65.3°(图6),导致并网电流功率因数的下降,影响基波电流跟踪能力.

为消除LPF对基波电流跟踪性能影响,可将滤波器从锁相环支路中“拆分”出来,形成单独的并联阻抗,如图5(a)所示.基于上述思路,本文采用串联-并联等效变换的方式,形成含低通滤波器的独立并联校正支路,如图5(b)中红色支路所示.则图5(a)中PLL等效阻抗(s)表示为Z.pll(s)=Zpll(s)‖ZLPF(s),其中ZLPF(s)为LPF支路通过upcc(s)反馈引入的并联阻抗,其表达式为式(8)

并联阻抗的特性主要由较小阻抗决定[8],因此可增大ZLPF(s)在基波处的幅值,来削弱ZLPF(s)对输出阻抗的影响,以实现提高逆变器电流跟踪性能的目的.

式(8)分子中各项参数均由系统决定不可更改,故从分母入手.ZLPF(s)分母含有的准PR电流调节器Gc(s)在基频处具有无穷大增益,极大影响了ZLPF(s)的幅值,为了增大可优化的范围,独立优化并联校正支路,利用作用点等效原则,将并联支路作用点移动至电流调节器后,得到图5(c)中红色支路.其中

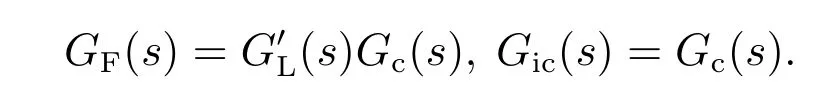
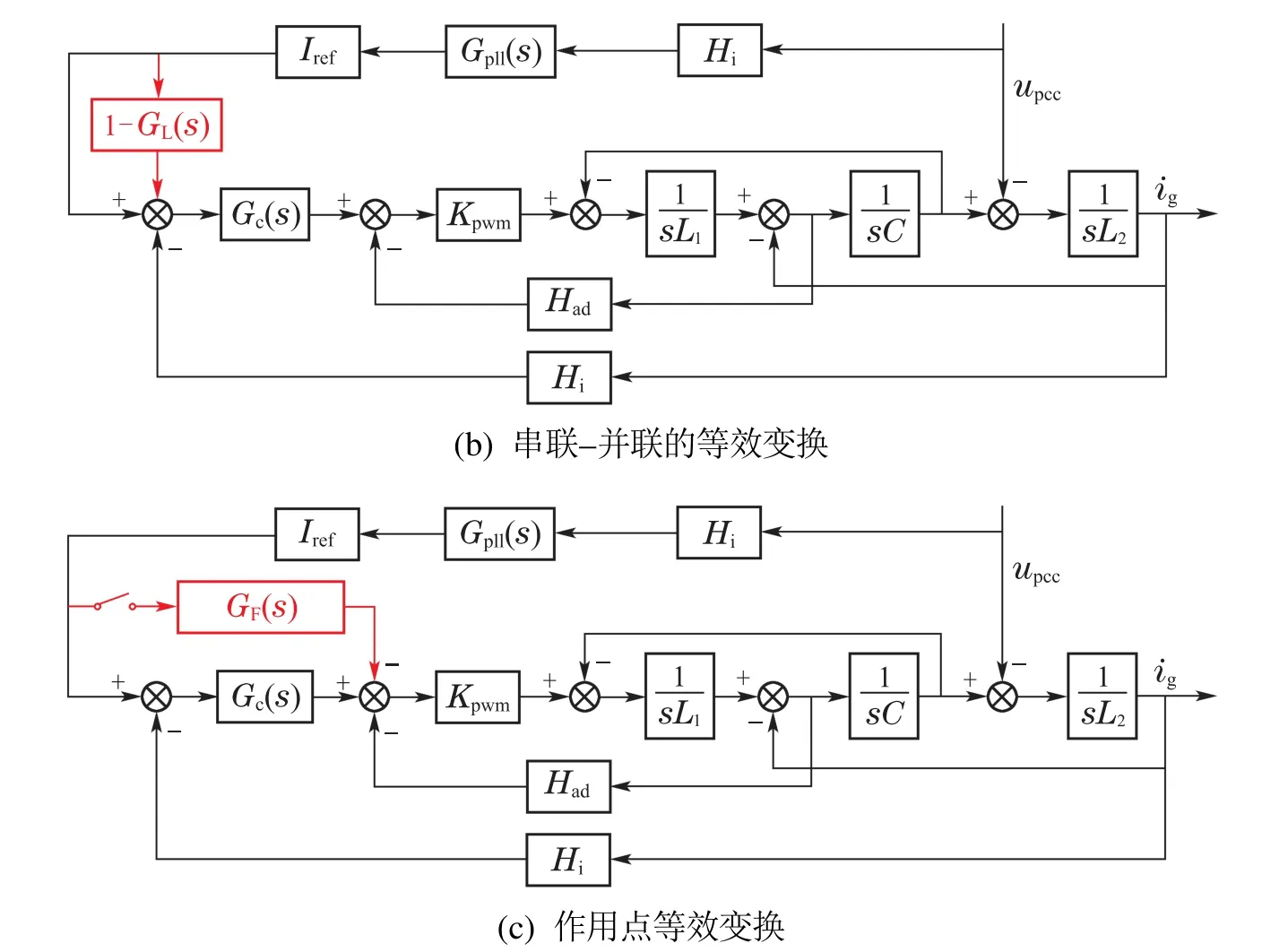
图5 基于电流二阶校正的等效变换框图Fig.5 Block diagram of equivalent transformation based on current second-order correction

进一步,可通过削减GF(s)在基频处的幅值,实现增大ZLPF(s)基波处幅值的目的.下面将分别对(s)和Gic(s)进行优化.

(s)包含了高通滤波器和带通滤波器,如式(9)所示:

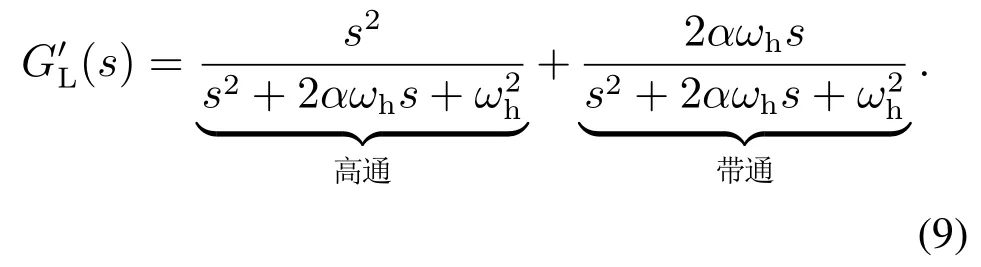
在ωh=416 rad/s,α=0.6参数条件下,带通滤波器的作用频段为38 Hz～116 Hz,在基波附近增益最大,为削减基波处幅值可将带通部分省略.则(s)可简化为(s).

将式(11)写成形如式(12)的零极点一般式:

其中:X为等效零点,Y,Z为等效极点,其值均大于零.

式(12)中,如采用表1的参数,虽能保证基频无相差,但会减小相位裕度,甚至在SCR=2时出现系统失稳.而单一的参数优化,如增大零点X可提升和电网阻抗交点处的输出阻抗相位,但会降低交点处幅值,如图6中曲线1所示:减小极点Y,Z可提高输出阻抗的幅值和相角,但会降低小于50 Hz频段的幅值,如图6中曲线2所示.

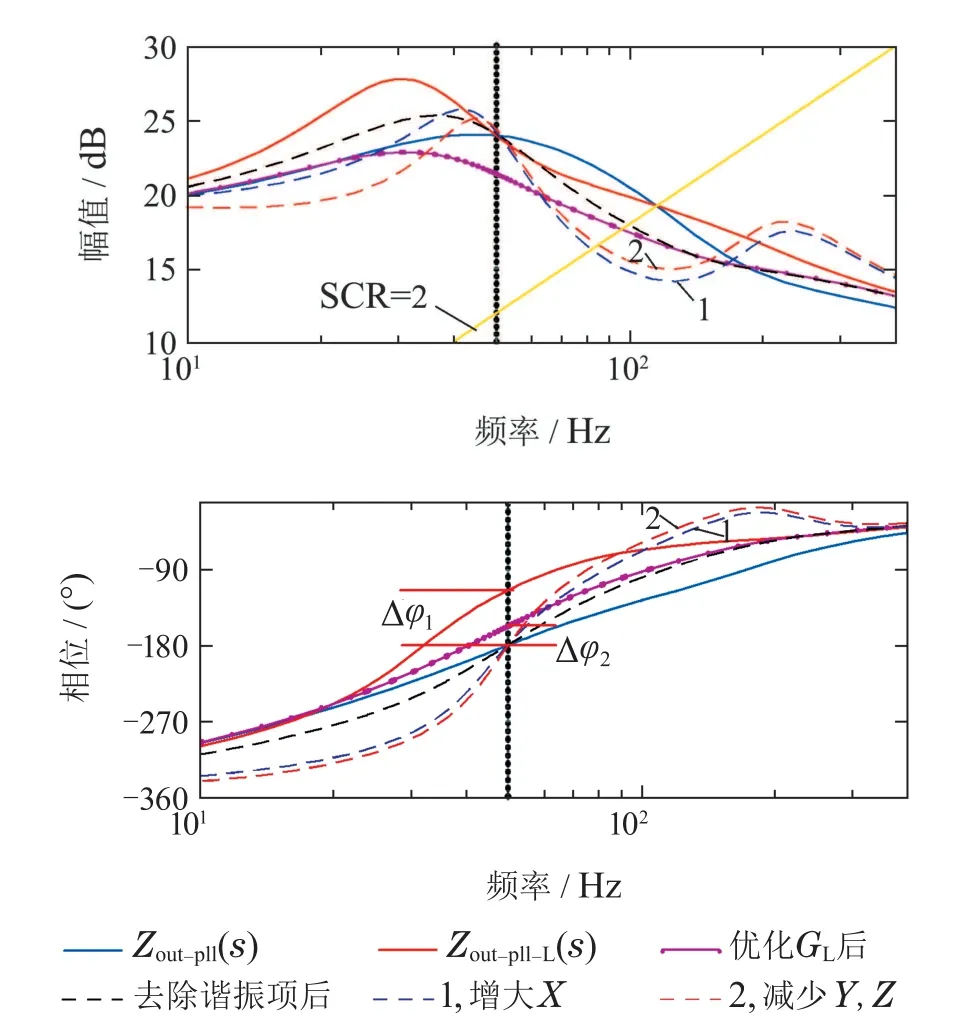
图6 不同改变后输出阻抗曲线Fig.6 Impedance curves after different changes

因此本文以基波电流控制性能、相角裕度、低频幅值为约束,对式(12)中的参数X,Y,Z进行联合优化,以获得更好的系统性能.同时该环节是独立支路,可使逆变器仅在弱电网下投入该环节以改善稳定性,而不需要调整原有控制器的参数.

4 基于多目标约束的二阶环节优化设计

为确保所加入的二阶环节GF(s)既能对宽范围的电网阻抗有较强的适应性,又能保持较好的电流跟踪性能.现以基波相位和幅值、系统稳定裕度以及低频幅值为约束对GF(s)的等效零极点进行设计.

4.1 基波电流跟踪性能

为简化计算,分析低频特性时忽略滤波电容C[18],此外HiKpwmGc(s)项中准PR控制器Gc(s)在基波处增益近乎无穷大,s(L1+L2)项可被进一步省略,故并网逆变器输出阻抗可简化为式(13)

为减小对基波电流跟踪性能的影响,需保持逆变器输出阻抗重塑前后基波处特性不变,因此从基波的幅值和相位两方面对其进行约束.

1) 基波幅值约束.

此时GF(s)对基波增益的影响可以忽略.假设

时,则可近似认为基波幅值不变,其中AMeorr−max为最大幅值比,据此可以得到基于基波幅值误差的约束条件

2)基波相位约束.

假设引入GF(s)项前后系统并网功率因数存在误差PFeorr,Δφ为对应功率因数误差角,若PFeorr满足PFeorr≤PFeorr−max时认为逆变器实现单位功率因数并网(PFeorr−max为容许的最大功率因数误差),则根据该条件有|Δφ|=Δφmax成立,Δφmax为对应PFeorr−max的功率因数误差角.

根据上述约束要求,可得到式(15)所示的关于逆变器输出阻抗的基波相位误差约束条件.考虑该约束后无需再加入基频相位校正环节.

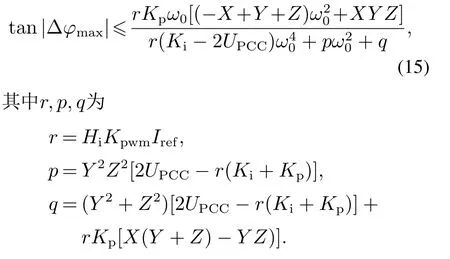
式(14)-(15)给出了基波电流跟踪性能对零极点设计的约束.令AMeorr−max=1%,PFeorr−max=0.1%,可得到图7所示的零极点初步取值范围.可以看出,式(14)包含于式(15)对应的取值范围(平面以上部分),故对电流跟踪性能的约束可简化为对基波幅值误差的约束.

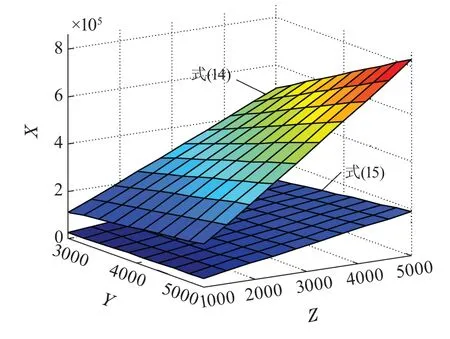
图7 受基波幅值与相位约束的零极点取值范围Fig.7 Range of poles constrained by fundamental amplitude and phase

4.2 系统稳定裕度

为保证Zg(s)在较大范围内变化时并网系统依然具有足够稳定裕度,本文考虑最恶劣的工况,即以SCR=2为基准设计并联阻抗参数.

在工程应用中,PM=30°即认定系统达到稳定.考虑式(13)简化前后存在的相位误差,为确保系统具有足够的稳定裕度,令PM=30°+θ,本文θ取10°,得到关于系统稳定裕度的设计约束条件为

在式(14)-(15)(17)约束下,重塑阻抗后的逆变器输出阻抗Bode图如图8所示.由图8可以看出,添加系统稳定裕度约束后并网逆变器稳定性大大提高,SCR=2的条件下无简化的系统PM提升至38°.但阻抗重塑后,交点位置可能发生变化,同时输出阻抗基频以下频段阻抗幅值较低,甚至低于0 dB从而与Zg(s)出现多个交点,不利于系统稳定.因此需要以低频幅值为约束对GF(s)参数取值范围进一步优化设计.

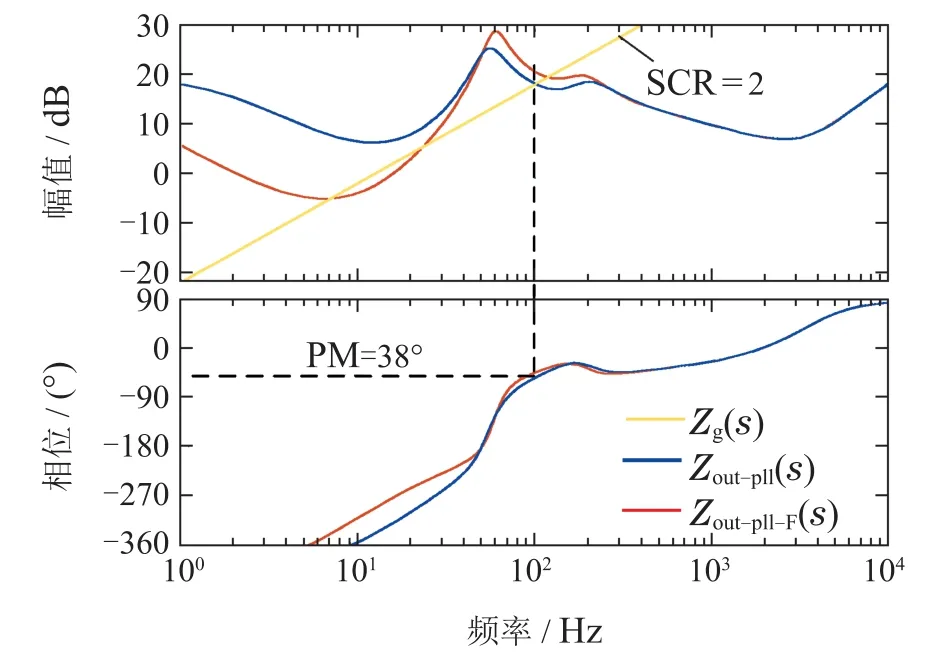
图8 不同零极点参数条件下的Zout−pll−F(s)bode图Fig.8 Frequency responses of Zout−pll−F(s) with different pole parameters

4.3 低频幅值约束

为保证基频以下逆变器输出阻抗与Zg(s)幅值无交点,在Zg(s)为感性条件下有式(18)

其中:Zg(jω0)为电网基波阻抗,K为Zg(s)在[0,50 Hz]区段幅值的最大值,文中取SCR=2,则Zg(jω0)的幅值略大于10 dB,K可取10 dB.由图8可以看出,输出阻抗与Zg(s)在基频以下的交点均在基频幅值K的下方,因此,只需将[0,50 Hz]区段输出阻抗提升至K以上即可消除低频交点.

式(13)表明直接求取逆变器输出阻抗模值仍较为复杂,需进一步简化式(18)的约束条件.由图5(a)可知,逆变器输出阻抗可由PLL等效阻抗(s)和逆变器阻抗Zout(s)并联获得,由于在[0,50 Hz]区段内,(s)的模远小于Zout(s),则式(18)的约束条件可进一步简化为将式(20)代入式(19)可得

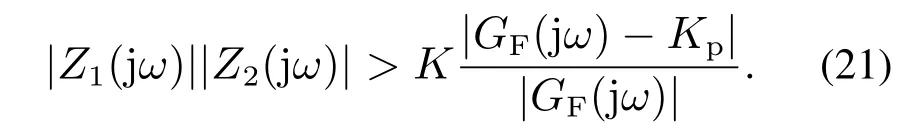
由于式(21)右边大于0且小于K,故若要式(21)成立,则应满足

为了约束[0,50 Hz]频段内阻抗特性的同时不影响其它与电网交互频段的特性,要求[0,50 Hz]区段在约束后,阻抗交点位置维持不变或上移.这意味着在式(14)(17)约束下的阻抗交点ωg处还应满足式(27)的约束.

基于约束式(14)(17)(22)(27)的并联阻抗参数取值范围如图9所示,图中红色曲线所围区域为同时满足上述多目标约束的等效零极点取值范围.

图9 等效零极点取值范围Fig.9 Range of equivalent poles

图10给出了重塑前后逆变器输出阻抗的bode图:在SCR=2的弱电网条件下,加入GF(s)校正环节后逆变器的相位裕度由-28°提升至2.6°,符合实际工程要求.Zout−pll−F(s)在基频处相位偏移1.08°,该偏移量在约束范围内,可认为并网逆变器以单位功率因数并网.

图10 逆变器输出阻抗Bode图Fig.10 Frequency responses of inverter output impedance

5 实验验证

本文搭建了基于StarSim实时仿真系统的并网逆变器实验平台,并以TI公司的DSPTMS320F28335为控制核心.实验平台如图11所示,系统参数与表1一致.

图11 实验平台Fig.11 Experiment platform

实验1弱网下加入LPF环节前后对比实验.图12(a)为Lg=6 mH(SCR=4.3)条件下,不加任何校正环节的并网电压电流波形.由图12(a)可以看出,upcc与ig的波形均产生严重畸变,并网系统稳定性亟需改善.当加入LPF环节时,实验波形如图12(b)所示,并网电流谐波总畸变率(total harmonic distortion,THD)降为2.38%,有效改善了并网电流的质量,但导致了ig相位的滞后,降低了系统并网功率因数.

图12 弱网下加入LPF前后实验波形Fig.12 Waveforms before and after by adding LPF to a weak network

实验2加入基于电流二阶校正的多目标约束并联阻抗实验.图13为弱电网下采用基于多目标约束的并网逆变器阻抗重塑方法的实验波形,其中二阶环节实验参数为X=2275,Y=154,Z=80.图13(a)为Lg=6 mH时并网电压与电流波形,其中并网电流THD为2.05%,且并网电压与并网电流无相差.图13(b)则表示当电网阻抗进一步增大,Lg=12.8 mH(SCR=2)时,并网电流THD依然仅为2.86%,且并网电压与并网电流无相差.实验验证了多目标约束的并联阻抗法在电网阻抗有较大变化时仍适用.

图14为Lg=12.8 mH时,二阶环节参数X,Y,Z只有其中一个满足约束时的并网电压电流波形,3组实验参数分别为X=2275,Y=250,Z=150;X=1500,Y=154,Z=150;X=1500,Y=250,Z=80.由图13-14可以看出,当只有一个参数满足约束时,并网电流无法达到稳定,而将X,Y,Z调整为同时满足约束条件时,并网电流重新稳定,实验验证了多目标约束的有效性.

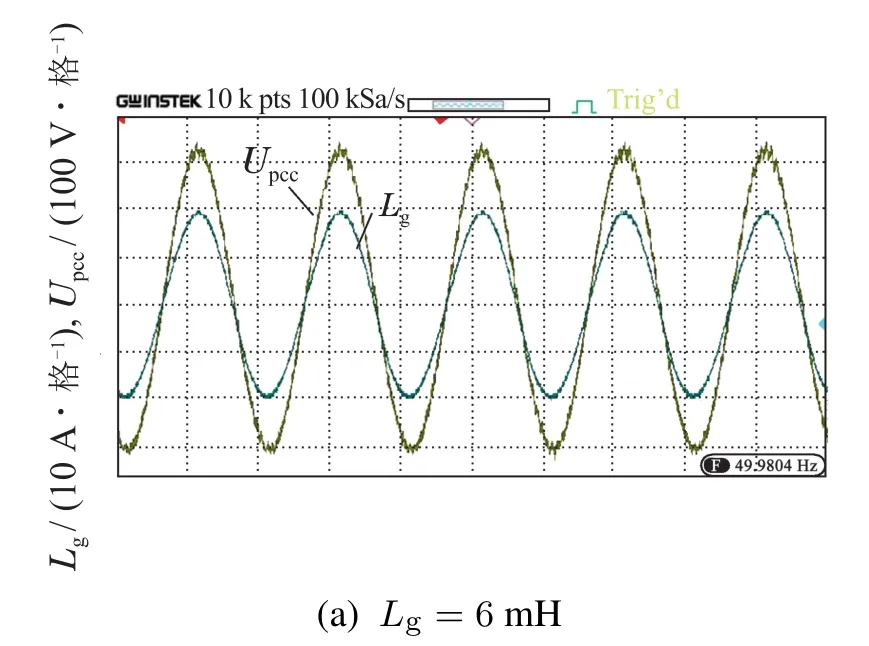
图13 多目标约束的并联阻抗矫正实验波形Fig.13 Shunt impedance correction waveforms with multiobjective constraints

图14 多目标约束的有效性验证Fig.14 Validation of multi-objective constraints

实验3动态性能测试.图15为Lg=12.8 mH时,在多目标约束阻抗重塑条件下ig(s)瞬态实验波形,电流参考值在T时刻从20 A增大至40 A,由图15可看出,系统具有良好的瞬态响应性能,且并网电压与电流无相位差,该结果进一步说明了所提方案的有效性.

图15 电流参考值突变时系统瞬态响应Fig.15 Transient response to a sudden change in the current reference

6 结论

为减小PLL串联滤波器对基波电流跟踪性能的影响,本文利用阻抗“拆分”的方式提出一种并联二阶校正回路的虚拟阻抗方法,并基于电流追踪性能、稳定性和低频幅值等多目标约束条件对所提出的二阶环节的零极点进行了多目标优化配置.

作为并联环节,所提出的校正回路可独立优化,在弱网下按需投入,在改善系统稳定性和实现单位功率因数并网的同时,不需要调整原有控制器的参数.

实验验证了本文所提控制方法和参数设计方法的有效性.