基于油液监测的风机主齿轮箱磨损预测*

许少凡 李秋秋 覃楚东 杨智宏 何伟楚

(广州机械科学研究院有限公司设备润滑与检测研究所 广东广州 510000)

风力发电是一种新能源发电方式，具有清洁可再生、装配施工周期短、占地面积少等特点，可以带来较好的经济与和社会效益，受到世界各国的重视[1]。作为可以将风能转化为电能主要设备，现代风力发电机组(简称风电机组)得到了迅速发展[2]。风能丰富的地区往往是环境恶劣的、偏僻的、交通不发达的山区、郊区或广袤的海上，外界环境会导致设备运行受到影响，显著降低其工作可靠性[3]。虽然技术的发展降低了风电机组的故障率，但相较于蒸汽轮机、燃气机等传统发电设备，风电机组的故障相对更频繁。风电机组较为常见的故障是关于电气和控制系统的，此类故障较好解决，机组停机时间短；而故障率较低的齿轮箱等传动系统的设备一旦出现问题，就需要较长的维修时间，影响日常生产效率与收益。因此保证风电机组平稳运行与安全生产，对风力发电具有重要的意义。

FENG 等[4]对风力涡轮齿轮箱的典型故障模式进行总结，运用监控控制系统与数据采集系统(SCADA)的整合数据，建立齿轮箱中温度、效率、转速与功率之间的关系，对齿轮箱故障进行预测。SHI 等[5]研究了基于模态应变能量(MSE)变化的结构损伤检测方法，讨论了测量噪声和截断分析模式形状的影响。李静立等[6]在环境荷载激励下，对模态参数进行识别和计算，通过阶次分析方法，在线分析风电机组齿轮箱系统模态，并搭建了可以应用在风电机组的在线模态参数识别和故障诊断系统。QIAN和YAN[7]运用盲源分离算法，将经过预处理的信号分解为稳态和非稳态分量，通过分析确定潜在故障特征频率。叶舟等人[8]建立正常状态和齿轮故障状态下的传动系统动力学模型，对比分析了2种状态下系统的输出响应。黄必清等[9]运用相关系数法、劣化度分析法和模糊综合评价等多种方法建立风电机组运行状态评价模型。

风电机组的构成复杂，系统较多[10]，关于风电机组齿轮设备的故障诊断多是对于齿轮箱本身的数据进行挖掘，而运用油液监测技术[11]进行故障诊断的研究相对薄弱。

本文作者对油液监测中的数据进行分析与挖掘，根据齿轮箱磨损情况与在用润滑油理化指标之间的关联性，拟合出一种风电机组主齿轮箱故障预测方程，运用偏最小二乘回归分析方法与灰色等维递补算法构建主齿轮箱磨损状态的模型，由此预测磨损情况，对设备运维策略提供指导性依据。

1 构建模型

灰色预测法是基于灰色系统理论，通过建立近似差分微分方程从而对系统进行模糊预测的一种方法[12]。

1.1 灰色等维递补预测模型

1.1.1 传统GM(1，1)模型

设变量X(0)=[x(0)(1)，x(0)(2)，…，x(0)(n)]为预测对象的非负序列，进行一次累加1-AGO(accumulating generation operator)生成一次累加序列：

X(1)=[x(1)(1)，x(1)(2)，…，x(1)(n)]

(1)

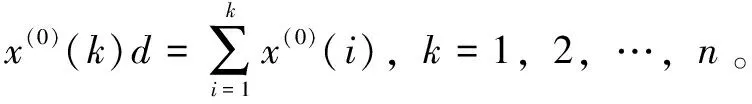
Z(1)为X(1)的紧邻均值生产序列：

Z(1)=[z(1)(1)，z(1)(2)，…，z(1)(n)]

(2)

X(0)(k)+az(1)(k)=b

(3)

(4)

其中，a为发展系数，b为灰色作用量，得到：

(5)

式中：

(6)

最后代入初始值求出预测模型的时间响应函数：

(7)

1.1.2 灰色等维递补GM(1，1)算法

灰色等维递补模型是在传统GM(1，1)的基础上，改变变量，不断更迭，不断修正模型参数。具体做法为：

(1)建立GM(1，1)模型，并对第n+1次的信息进行预测，得到x(0)(n+1)；

(2)将x(0)(n+1)作为最新数据加入原始序列，同时剔除原始序列中的最旧信息x(0)(1)，进行第一次新陈代谢循环；

(3)对第一次新陈代谢循环的序列再次建立GM(1，1)模型，对第n+2次信息进行预测，得到x(0)(n+2)；

(4)重复上述步骤，不断循环建模，满足系统预测要求为止。

1.2 偏最小二乘回归模型

PLS是多元数据统计分析的新型方法，既是特征抽取方法，也是回归算法[13]。PLS包含典型相关分析、主成分分析和多元线性回归分析等分析方法的优点，对所处理的数据筛选分析，进而提取系统携带的最好解释性的综合变量[14]。

1.2.1 PLS算法原理

设有p个自变量{χ1，χ2，…，χp}和q个自变量{γ1，γ2，…，γq}，为得出自变量χ与应变量γ间的统计学关系，对n个样本点进行测量，组成自变量与因变量的数据矩阵X=[χ1，χ2，…，χp]n×p和Y=[γ1，γ2，…，γq]n×q。

PLS分析分别在X、Y中提取主成分t1与u1，提取过程中需要满足2个要求：

(a)t1与u1尽可能大地携带数据矩阵中的变异信息，即：

Var(t1)→max

Var(u1)→max

(b)t1与u1相关程度达到最大，即：

r(t1，u1)→max

PLS算法基本原理如图1所示。

图1 PLS原理模型

1.2.2 建立模型

PLS算法思想如下：

(1)对X与Y进行数据标准化，可以得到数据矩阵E0=[e01，e02，…，e0p]n×p，F0=[f01，f02，…，f0q]n×q，其中e0k和f0j分别为第k(k=1，2，…，p)个自变量、第j(j=1，2，…，q)个因变量的标准化值。

t1=E0w1

(8)

u1=F0c1

(9)

之后得到E0、F0对t1、u1的2个回归方程：

(10)

(11)

式中：m1、r1为回归系数向量；E1、F1为残差矩阵。

(12)

(13)

(3)根据得到的残差矩阵E1、F1取代E0、F0，求第二个轴w2、c2及第二个主成分t2、u2。上述步骤进行重复，则依次得到主成分。

设X的秩为A，则最终回归方程的形式为

(14)

其中FAk为残差矩阵FA的第k列。

1.2.3 模型验证

建立PLS模型后，运用h个成分对因变量数据矩阵Y进行拟合，依据交叉有效性原则对其验证，有：

(15)

1.3 灰色等维递补GM(1，1)-PLS模型

灰色等维递补GM(1，1)-PLS组合预测模型原理与流程如图2所示，对数据进行偏最小二乘回归分析，得到相关变量间具体函数关系，利用灰色等维递补GM(1，1)预测法对油品各类理化指标进行模糊预测，将得到的预测值与实际值进行整合，并对未来一段时间的指标进行预测，可以提早应对可能出现的异常磨损情况。

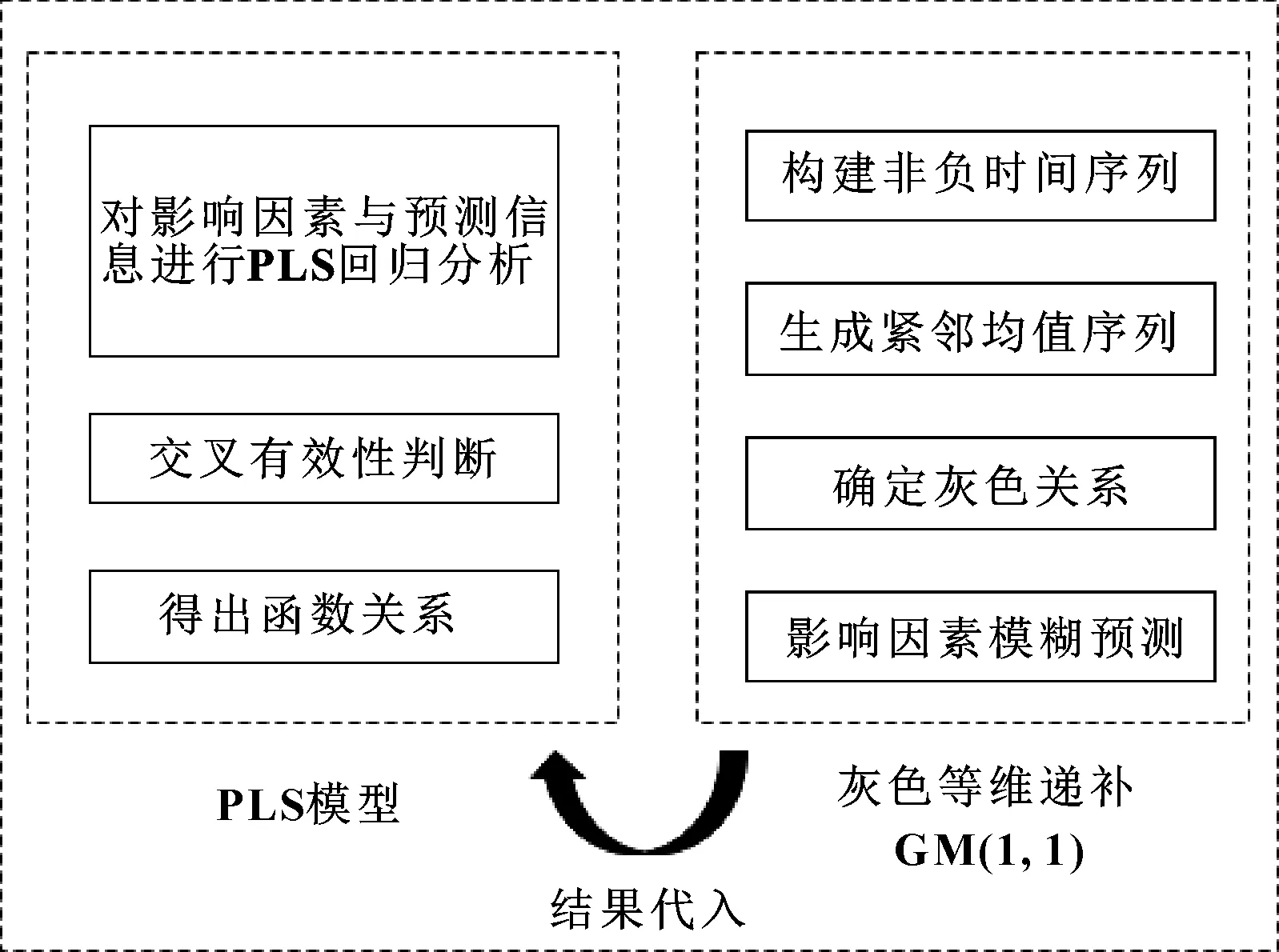
图2 组合预测模型与流程示意

2 试验分析

自2014年来，对某风电集团有限公司的风场主齿轮箱在用油进行监测，获得润滑与磨损情况，并进行油液监测多源信息融合[16]。油液监测信息融合策略流程如图3所示。1号风电机组主齿轮箱润滑油为某品牌320#齿轮油，检测标准为NB/T 10111—2018(ISO VG 320)。

图3 油液监测信息融合流程

2.1 油品数据信息

1号主齿轮箱润滑油理化指标与相关磨损情况如表1所示。

表1 油液监测理化数据

运动黏度和酸值能够对在用齿轮润滑油的理化指标和氧化性能进行判定；Si元素含量通常来源于外界，可以反映设备的密封状况；Zn、P等元素属于润滑油添加剂中的成分，可以反映润滑油本身相关信息，能够判定润滑油添加剂损耗情况以及存在的污染；Cu与Fe作为主要的检测磨损元素，通常可以直接反映设备的磨损状况，但有时会因取样位置而导致差异，其理化指标箱型图如图4所示。

图4 油液监测理化指标箱型图

润滑油理化指标数据整体处于正常范围内，箱型图显示污染元素Si含量存在一个离群值，可能是因为设备密封性能减弱导致。

2.2 建模分析

数据经过标准化处理可以得到矩阵：

E0=

经过标准化后得到的回归方程为

y=1.536 5-0.162 0x1-0.039 7x2+0.365 1x3-0.053 2x4+0.577 4x5-0.143 5x6

(16)

式中:y为铁元素含量;x1、x2、x3、x4、x5和x6分别对应油液监测数据中的运动黏度、酸值、铜元素含量、硅元素含量、锌元素含量以及磷元素含量。

由图5所示得分可知，样品1、2分为一类，样品3、4、5分为一类，样品6、7分为一类，可以直观地将理化性质相近的润滑油分组。

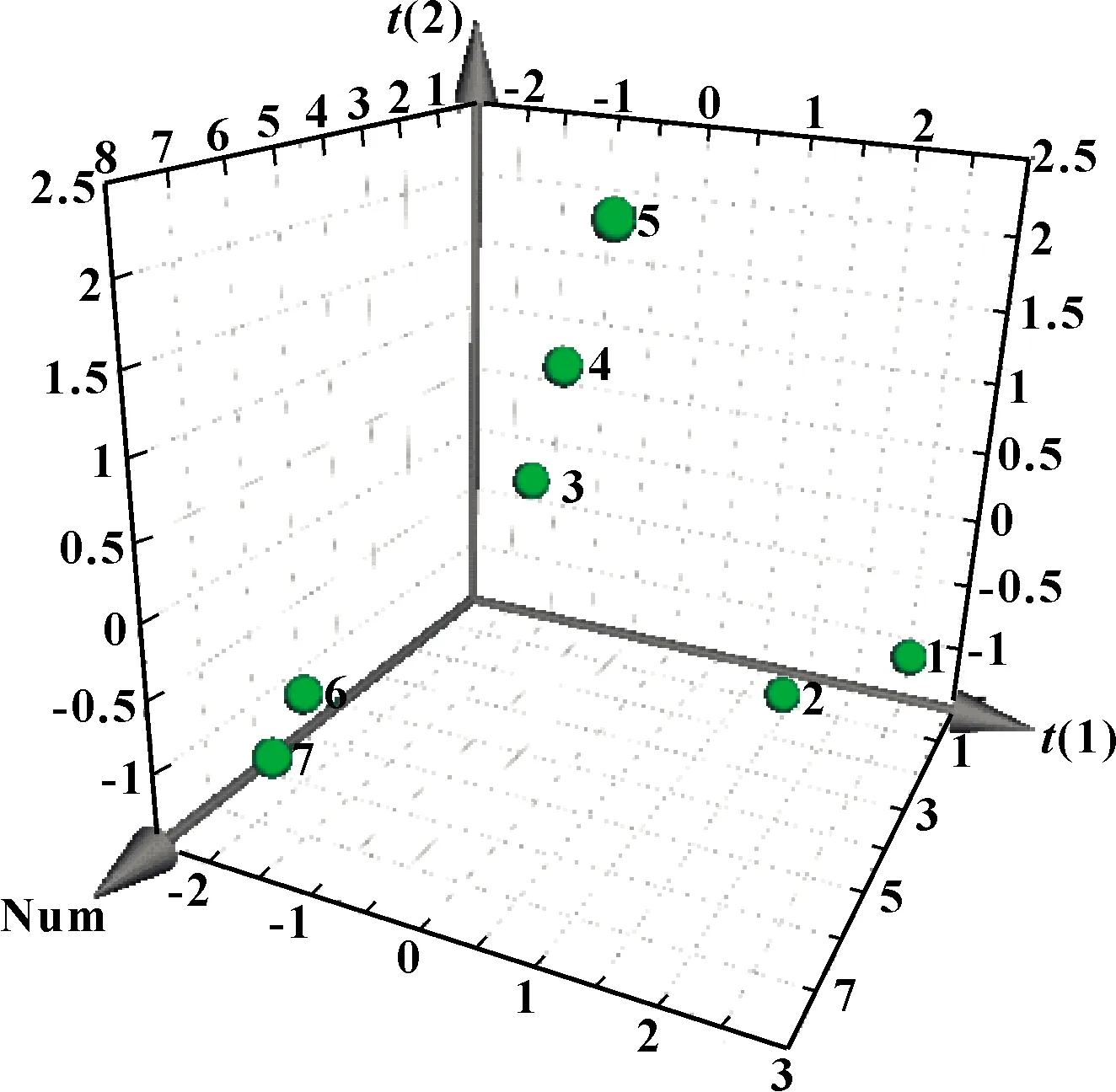
图5 PLS模型得分

将标准化结果进行还原，所得到最终回归方程为

y=242.225-0.647x1-5.869x2+1.404-0.208x4+1.662x5-0.063 8x6

(17)

提取主成分后，将t与u绘制成为坐标，如图6所示，说明出应变量与自变量具有较强的相关性。

图6 t/u平面坐标

齿轮箱的磨损情况在正常润滑情况下是处于缓慢衰变的状态，因此油液监测所得到的各项理化指标数据是维持一定的动态平衡，数值变化不会很大。但当齿轮箱中出现异常磨损，这个动态平衡遭到破坏，导致数据出现较大波动，预测值与实际值产生较大偏差，根据这些异常偏差可以对齿轮箱进行预测诊断，及时消除隐患，避免产生更大的经济损失。

2.3 数据拟合

为验证主齿轮箱的PLS回归方程的准确性，选取同批次送检工况相近的2号主齿轮箱的相关油液监测数据对其进行PLS拟合，如表2所示。将该设备检测数据代入到公式中，得到预测值与实际值，拟合结果如图7所示，证明PLS回归方程具有一定的预测性与有效性。根据回归方程，可以快速且准确地预测出实际磨损情况。因此，构建的PLS模型可以应用到齿轮箱的故障诊断中。

表2 2号主齿轮箱的油液监测理化数据

图7 2号主齿轮箱拟合情况

3 预测应用

对表1中的数据进行灰色等维递补模型拟合，预测未来2年的润滑油理化指标数据，如表3所示。

表3 灰色等维递补模型预测未来2年油液数据

将未来2年的理化性质数据代入PLS方程中，得到Fe元素的预测值，如图8所示，结果表明1号主齿轮箱在稳定运行、维护正常的情况下，理论上Fe元素质量分数在2021年时会上升，2022年会轻微下降。与传统灰色等维递补模型预测的值相比，GM(1，1)-PLS所预测的Fe元素含量较低，但趋势保持一致。所以建议未来2年的风机齿轮箱维护策略维持现状。

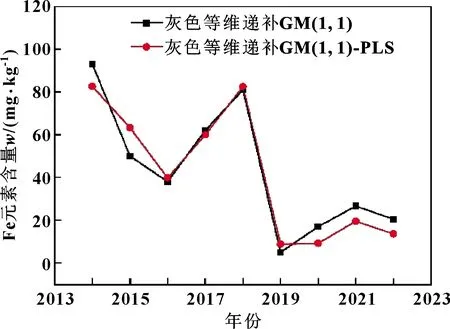
图8 Fe元素含量预测数据拟合结果

4 结论

针对齿轮箱运行过程中的磨损问题，在分析齿轮箱油液信息的基础上，融合2种算法，构建灰色等维递补GM(1，1)-PLS模型，通过对齿轮箱数据分析拟合，得出以下结论：

(1)运用偏最小二乘回归方法所拟合出的线性回归方程可以较为准确地判断齿轮箱中的异常磨损元素含量，从而提高生产效率，对设备维护与快速诊断提供重要依据；

(2)模型对油液监测中的实例同样可以有效预测，其预测结果符合工程实际情况；

(3)采用灰色等维递补GM(1，1)-PLS对磨损情况进行预测，对制定风机齿轮箱维护策略具有指导意义。