带螺旋槽和双向微通槽动静压气体轴承静态特性研究*
李树森 穆岩璞 马添潇
(东北林业大学机电工程学院 黑龙江哈尔滨 150040)
动静压气体轴承是影响超精密加工精度的重要零部件,它具有速度高、精度高、无污染、摩擦损耗小和寿命长等突出优点。然而,动静压气体轴承承载能力较小,在一定程度上限制了其广泛应用[1-2]。人们在改善动静压气体轴承性能方面不断探索,取得了许多成果。
动静压气体轴承相比静压气体轴承和动压气体轴承有着特性好和不易产生气锤现象等优点。王欣崎等[3]以螺旋槽小孔节流动静压气体轴承为研究对象,研究槽深、槽宽等参数对静态特性的影响。汪久根等[4]针对螺旋槽轴承的设计制造、润滑理论等方面提出了螺旋槽的分析方法。于贺春等[5]分析了人字槽狭缝节流动静压混合气体轴承并通过仿真优化了该轴承设计参数。李树森和王成成[6]以开设轴向微通槽气体轴承为研究对象,分析气膜厚度、槽宽、槽深等对承载力的影响,获得了微通槽最佳参数。当前,动静压气体轴承已有一定研究基础,但在结构理论方面并不完备,微通槽结构设计较为单一,仍需深入研究。
本文作者设计了一种具有螺旋槽和双向微通槽的动静压气体轴承,使用Fluent对其静态特性进行研究。通过开设螺旋槽提升轴承的动压效应,同时通过设计新型的双向微通槽避免由小孔节流产生气锤自激的振动现象,从而提高轴承承载力和刚度,为动静压气体轴承优化设计提供理论基础。
1 带螺旋槽和双向微通槽动静压气体轴承结构和工作原理
图1所示为带螺旋槽和双向微通槽动静压气体轴承的结构简图。轴承上具有小孔节流器和双向微通槽,主轴上有螺旋槽,轴承开设双排供气孔,每排8个。双向微通槽由轴向和周向微通槽组成,轴向微通槽沿轴线开通设有8条,沿轴承内圆周方向均布,并连接同一轴线上分别位于不同两排的小孔节流器出气口;周向微通槽有2条,沿周向分别开设于双排小孔节流器处,并连接同一周向上的小孔节流器的出气口。
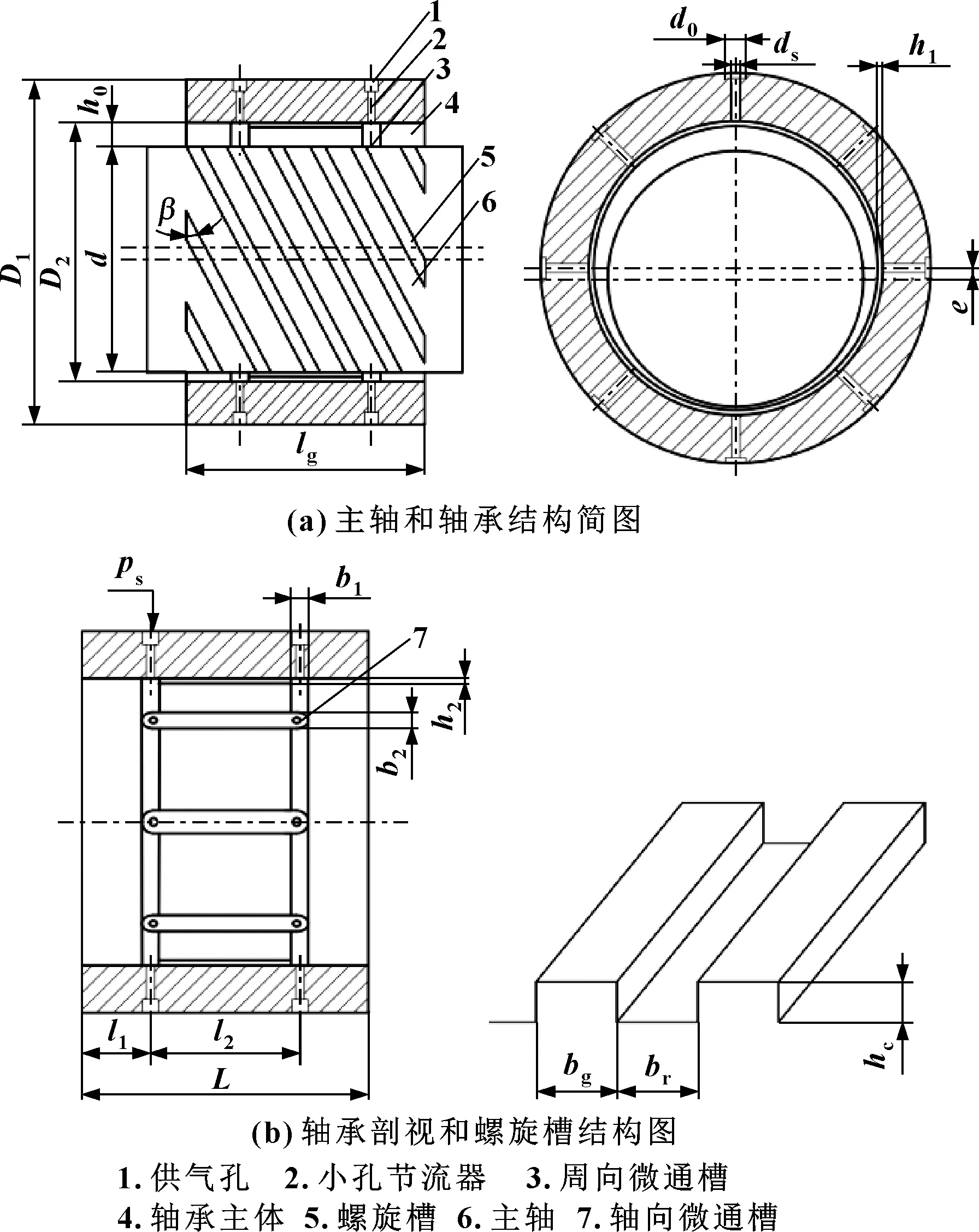
图1 带螺旋槽和双向微通槽动静压气体轴承结构示意
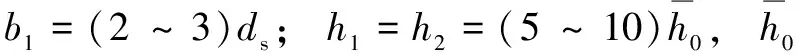

表1 气体轴承结构参数和工作参数
动静压气体轴承的工作原理是动压气体轴承和静压气体轴承工作原理的混合叠加。在开始阶段具有一定压力的气体从供气孔进入小孔节流器中,通过小孔节流器进入轴承间隙形成润滑气膜,使轴承具有一定承载力和刚度[8]进行静压承载。当主轴高速旋转时,通过轴颈回转以及螺旋槽带动轴承间隙内的黏性气体在黏滞力的作用下,产生压力升,从而具有法向支承能力,形成动压承载,进一步提升整个轴承的承载能力[9]。
2 仿真模型建立与静态特性理论分析
2.1 带螺旋槽和双向微通槽动静压气体轴承静态特性理论分析
利用有限元分析法求解雷诺方程对螺旋槽双向微通槽动静压气体轴承进行静态特性分析。
假设气体为理想气体,黏性系数为常数,气体流动为等温过程,考虑气体的可压缩性,气体在气膜间隙中不存在相对滑动,推导出雷诺方程如式(1)[10-13]所示。
(1)
式中:p为压力函数;ρ为流量密度;μ为气体动力黏度;vx、vz为气流速度分量。
引入量纲一化参数,取p0、hm、L为参考量,可得量纲一化雷诺方程如式(2)所示。
(2)
将狄利克雷函数δi引入,得到简化后的雷诺方程式(3)。
(3)
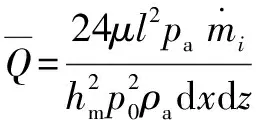
有限元分析的方法是通过将整个气膜分割成n个单元体,并对每个单元体进行求解计算,求出每个单元体的承载力Wλ,然后将所求得的每个单元体的承载力进行累加就可得到整个轴承的总承载力W,如式(4)所示。
(4)
而气膜刚度是指气膜在受力时抵抗弹性变形的能力,其计算公式如式(5)所示。
(5)
2.2 仿真模型的建立
通过Gambit软件对轴承的气膜模型进行网格划分,使用四面体网格划分,相比于六面体网格其对复杂细小结构的网格划分速度更快节点更多。使用自适应网格技术以此来保证网格无关性,并提升有限元分析的整体精度。划分的气膜模型网格如图2所示。

图2 气膜模型的网格划分示意
2.3 边界条件的设立
模型采用压力进出口边界和壁面边界,16个进气口设置压力为ps=0.4 MPa,出口边界压力设为pa=0.101 MPa;主轴转速n=1×105r/min;偏心率设置为0.5;壁面为移动边界,方向设置为旋转;流体介质为理想气体并为常温流动,湍流模型采用k-εSST模型[14],并且开启曲率矫正有效地改善边界层的梯度。
3 仿真结果与分析
3.1 不同偏心率微通槽对轴承静态特性的影响
图3所示为具有轴向微通槽结构的气体轴承仿真模型I、具有周向微通槽结构的气体轴承仿真模型II和具有双向微通槽的气体轴承仿真模型III,在假设偏心率为0.5时,气膜内部流场压力分布云图。
主轴高速旋转产生动压效应,在气膜厚度收敛位置会出现高压区域,在气膜扩大位置会出现低压区域。根据3种模型仿真压力云图可以看出,周向微通槽的各点压力最小,轴向微通槽的各点压力居中,使用双向微通槽的各点压力最大。由此可见,使用双向微通槽除了均压的作用外在主轴转动时可以产生一定的动压效果从而提升轴承内气膜流场各点压力。由图3可知,模型III中的最大压力值比模型II中提升了0.15 MPa,这表明双向微通槽可以进一步提升轴承动压效应[15],并且提升轴承承载性能。

图3 模型I、模型II和模型III气膜内部流场压力分布云图
改变偏心率进行分析,模型I、模型II和模型III的承载力和刚度随偏心率的变化曲线如图4所示。
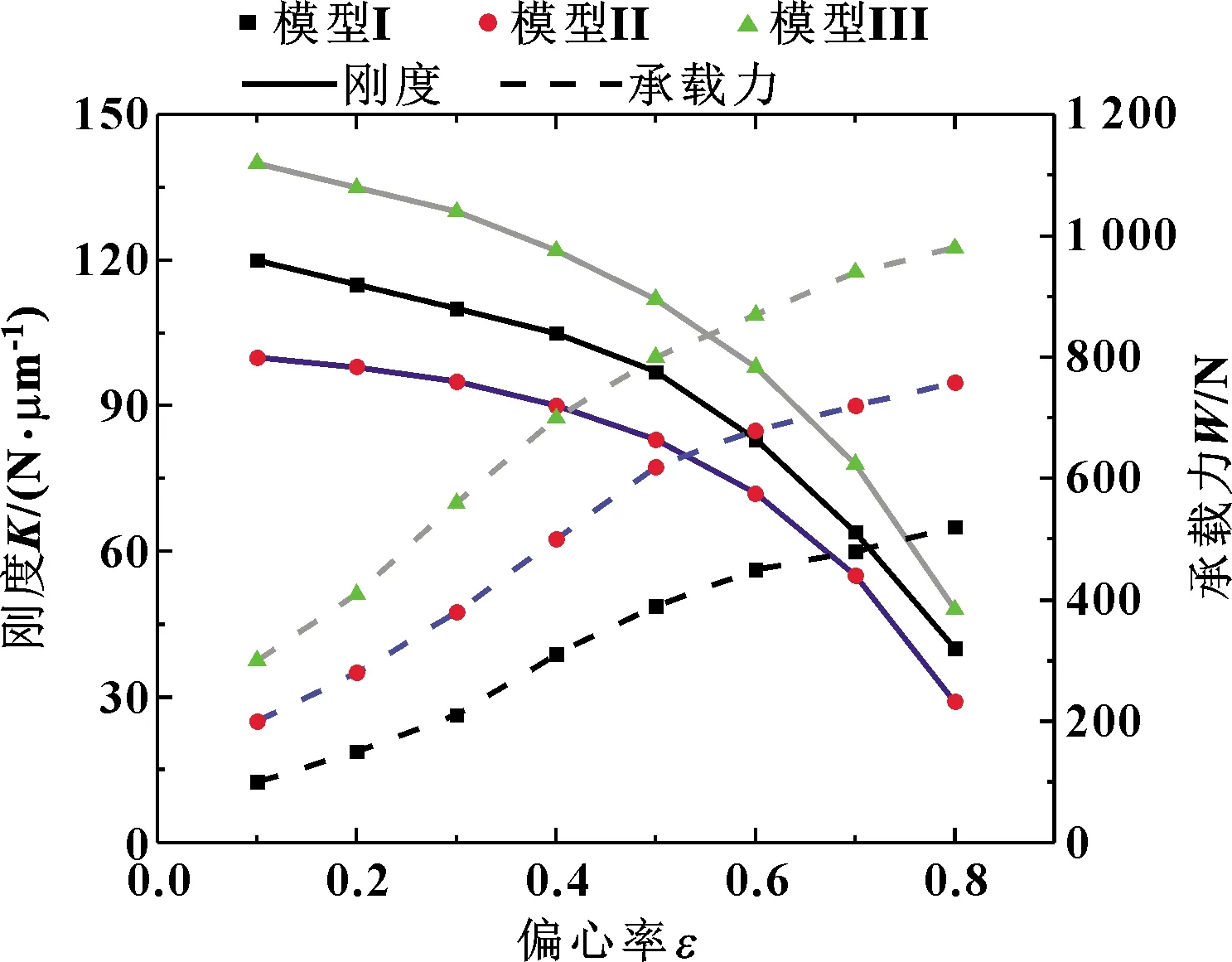
图4 偏心率与承载力和刚度关系曲线
由图4可知,随着偏心率的增大,各个轴承的承载力都在增大,且模型III和模型I的承载力增加值与模型II相比,其之间的差距逐渐增大,模型III的承载力和刚度明显优于模型II和模型I;并且随着偏心率的增加3个模型的承载力增加速度都在逐渐地下降。由此可见,带双微通槽轴承的承载力随着偏心率的增大而增大且增加速度逐渐减慢。刚度随着偏心率的增大而减小,且随着偏心率的增大衰减的速度也在加快。刚度的减小即轴承的承载稳定性逐渐降低,这种现象主要是因为偏心率的增大,导致轴承间隙中上下气膜厚度相差变大,压力差增大,即承载力增加。
综上所述,当轴承的偏心率过小或过大,都不可以满足轴承最佳的运转条件,偏心率过小会导致承载力较低,偏心率过大会严重影响轴承刚度。所以,可根据实际情况选取适合的偏心率,一般取值为0.3~0.6之间。
3.2 不同螺旋槽深度下主轴转速对双向微通槽轴承静态特性的影响
螺旋槽的开设使轴承的动压效应加大,且螺旋槽结构参数的改变也会对双向微通槽轴承的静态特性有所影响。将螺旋槽深度分别设为0.08、0.16、0.24、0.32 mm时,分别研究不同螺旋槽深度下主轴转速对双向微通槽轴承静态特性的影响。固定其他参数,得到承载力和刚度的变化曲线如图5所示。
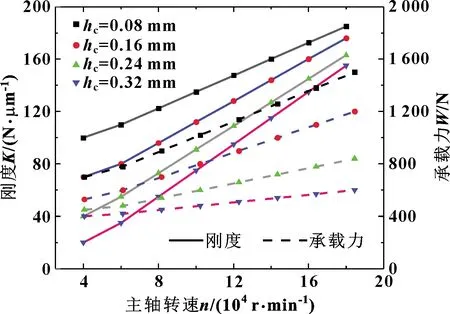
图5 主轴转速与承载力和刚度关系曲线
由图5可知,同一转速下主轴的承载力和刚度随螺旋槽的深度加深不断地减小,且随着转速的不断提高各螺旋槽深度的承载力差距不断地增大,这说明随着转速的提高螺旋槽的动压效应会相应地提高,而螺旋槽的深度越小则动压效应越好。在满足技术要求和理论计算的基础上可以选用相对深度较小的螺旋槽,以提升动静压气体轴承的承载力和刚度。
3.3 不同气膜厚度下双向微通槽的深度对气体轴承静态特性的影响
研究表明,双向微通槽在气膜厚度为15~25 μm之间的情况下具有较高的承载力和刚度。对不同气膜的模型进行仿真计算,得出不同的槽深所对应的静态特性曲线。在不同气膜厚度下双向微通槽深度与静态特性的变化曲线如图6所示。

图6 微通槽深度与承载力和刚度关系曲线
由图6可知,微通槽的深度取0.04~0.32 mm,当微通槽的深度小于0.2 mm时气体轴承的承载能力和刚度都逐渐提升,当超过0.2 mm后轴承的承载能力有小波动,但是并不是逐渐趋于稳定而是有下降趋势。这是因为微通槽深度增加到一定值后, 槽内的高压气体对槽附近的气膜影响不再提升。比较可知,气膜厚度为0.15 μm的气体轴承静态特性最好。由此可知,气膜厚度较小时轴承的承载力和刚度较好。
3.4 不同供气压力下双向微通槽的宽度对气体轴承静态特性的影响
双向微通槽的宽度和供气压力是动静压气体轴承的重要参数,其改变会造成轴承的静态特性变化。选取4个不同供气压力的模型进行仿真分析,结果如图7所示。
由图7可知,在同一供气压力下,当微通槽的宽度在0.6~1.2 mm之间时承载力和刚度都在逐渐增大;宽度大于1.2 mm以后承载力和刚度都有所下降。这主要是因为微通槽本身存在一定动压效应,随着宽度的增加,轴承间气膜厚度变厚,动压效应减弱,从而降低了承载力和刚度。同一槽宽下,供气压力越大承载力和刚度越大,但是达到1 MPa后变化减缓,因为随着供气压力逐渐增大,轴承内气体的流速转变为超音速,导致气膜流场出现激波、紊流等现象。
4 仿真结果可靠性验证
文中采用理论方法对模型仿真结果进行可靠性验证,理论求解所使用的参数与仿真参数相同。将所得到的结果进行对比,如图8所示。
由图8可知,仿真与理论计算得到的承载力和刚度比较吻合,说明仿真结果具有一定的可靠性。
5 结论
(1)开设轴向与周向的微通槽可提高动静压气体轴承的承载力和刚度,在一定范围内,偏心率越高承载力提升越显著。
(2)在一定的条件下,提高供气压力可以提高动静压气体轴承承载力,当供气压力到达一定值时会产生紊流现象,承载力不再提升反而有所下降。
(3)增加双向微通槽的深度可在一定程度上优化动静压气体轴承静态特性,随着双向微通槽宽度的增加承载力和刚度先增加后减小。
(4)螺旋槽可以产生动压效应提升承载力,主轴转速越高承载能力提升越大。
(5)相对于单向微通槽的模型I和模型II,使用双向微通槽模型III的承载力和刚度最优。

