舰载对陆巡航导弹规划航路点间距离的计算分析*

史岩，孙航，陈云阁，王珏

（海军大连舰艇学院a. 水面舰艇作战实验中心；b. 航海系；c. 作战软件与仿真研究所，辽宁 大连 116018）

0 引言

舰载对陆巡航导弹可以在距离目标更远的红方防护海域内进行发射，实现了在保护自身发射平台安全的前提下，对蓝方所属的陆地纵深目标实施精确打击的目的[1]。随着导弹巡航距离的增加，需进一步提高其航程计算精度。

在充分考虑导弹的各种约束条件以及实际航行区域的情况下，为导弹规划出一条满足某种或多种需求的航路是导弹航路规划的主要任务[2]。由于导弹实际飞行航迹需要近似大地线的要求，因此在航路的规划过程中，规划航路的航程计算精度就应该接近大地线的计算精度。目前，谢晓方等人提出利用Bowring 公式快速计算反舰导弹航路点间距离[3]，该方法编程简便，易于工程实现，但是考虑到舰载对陆巡航导弹可能规划出由海面到陆地的直接连通的规划航路情形，此时的航路点间会存在一定的高程差，因此从某种程度上影响了航路点间距离的计算精度。为了解决该问题，卫泽[4]等提出顾及空间两点间高程时的距离计算方法，但是该算法相比于Bowring 公式快速计算方法更加复杂。由于舰载对陆巡航导弹航路规划时，航路点间距离的计算是对规划航程的定量评估，因此有必要提出一套与导弹航路规划相匹配的规划航路点间距离的计算方法。本文在Bow⁃ring 反解公式[5]的基础上，通过建立顾及高程的地球椭球模型，兼顾了舰载对陆巡航导弹规划航路点间距离计算的精度和便捷性。

1 Bowring 公式相关内容

通常地球的大地水准面可近似为旋转椭球面，而大地距离是指在这个椭球面上任意两点之间大地线的长度，即两点的最短距离，对于导弹而言是两个航路点之间的直飞路径。导弹在规划航路时，首先需要耗时规划航路，则计算规划的航程需要顾及到计算的效率[6]。此外，导弹按照规划航路进行实际飞行的过程中，需要按照接近大地线的航线巡航飞行，则在计算规划的航程时应该尽可能地提高大地距离的计算精度。

在关于大地距离的计算中[7-8]有以数值积分为基础的Gauss 法[9]、牛顿法[10]，其精度随着距离的增加而下降，且计算工作量较大、较复杂。有以Bessel大地投影[11]为基础的公式法，其在计算过程中计算的精度与公式展开的项数有关，需要较为复杂的迭代过程。有以地图投影理论为基础的Bowring 公式法，其计算精度在短距离内较高，且计算过程较为简便，易于编程实现。由于导弹航路规划中航路段侧重于短距离（大地线计算可以按照距离长短分为400 km 以下的短距离计算，400~1 000 km 的中距离计算，以及1 000 km 以上的长距离计算[3]）范围的计算，因此该法较为适用。同时，考虑到舰载对陆巡航导弹航路规划中航路点之间存在较大的高程差时，需要在考虑高程差值的前提下对大地线距离进行计算。在现有的Bowring 公式快速解算大地线长度的基础上，利用顾及高程的地球辅助椭球模型参数的求取，重新推导顾及高程的Bowring 计算公式。

已知两点的经纬度坐标时计算两点间的大地线长度以及方位，需要利用Bowring 公式。设定椭球面上的两点P1(L1,B1)和P2(L2,B2)，a和b表示地球的长短半轴长度，e′为第二偏心率且有公式e′2=(a2-b2)/b2，具体公式见（1）~（12）。

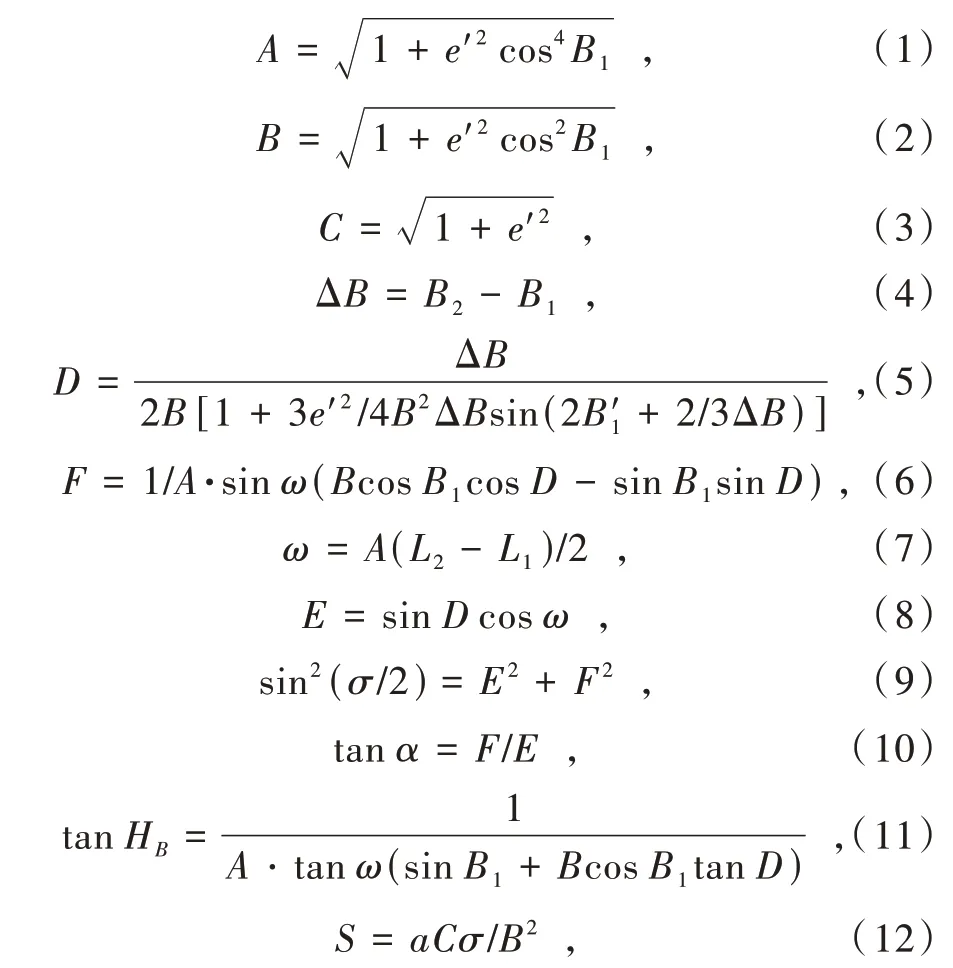
S表示点P1，P2之间的距离，从点P1到P2的方位角为α12，点P2到P1的方位角为α21，则

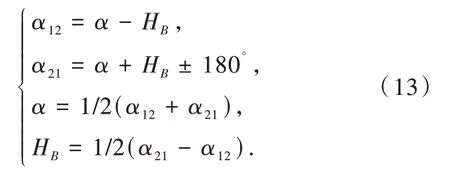
相关文献[12-13]指出，Bowring 公式的角度偏差较小，距离精度在300 km 内的计算误差仅为0.1 m，在700 km 内的计算误差仅为1 m，1 500 km 内的计算误差也只有l0 m，而到2 000 km 时的计算误差达到40 m。则可认为Bowring 公式在求解航路点距离时的精度较高，且由于航路规划中，航路点之间的规划航段多在中短距离之间，所以结合Bowring 公式精度及易于编程的特点完全可以应用在对陆巡航导弹规划航路段的距离计算中。由于上述Bowring公式的计算精度是基于无高程差时大地线长度的计算，为了更好地为导弹规划航路提供航程参考，Bowring 计算公式需要顾及高程差值。

2 顾及高程的地球椭球模型

地球参考椭球面上点的大地坐标为P(B,L)，其转换为空间直角坐标的公式为

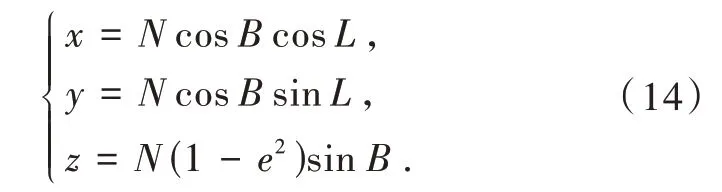
式中：e为第一偏心率，且有公式e2= (a2-b2)/a2。不在地球参考椭球面上点的大地坐标P(B,L,H)，其转换为空间直角坐标的公式为

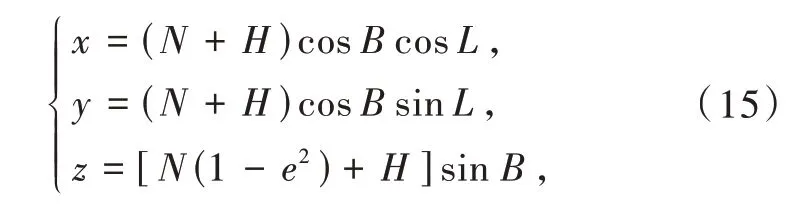
设定高度的平均值为Hm，做中心与地球椭球的中心保持一致的辅助椭球（辅助椭球参数为af，bf），同时辅助椭球上x,y,z坐标轴指向、扁率，也与地球椭球保持一致[14]，结合图1 所示，则有

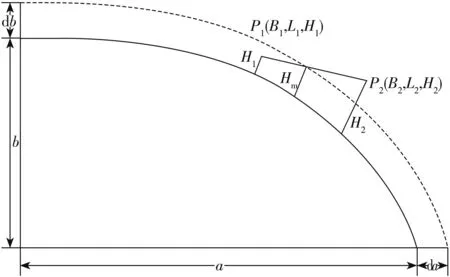
图1 辅助椭球示意图Fig.1 Auxiliary ellipsoid diagram

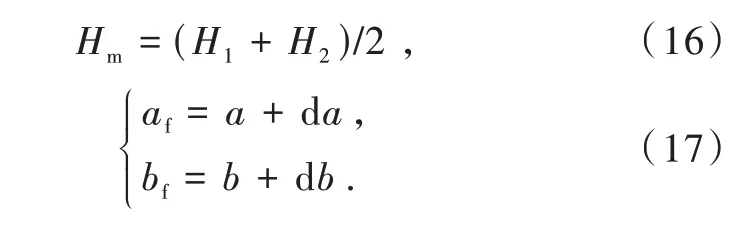
同时满足如下关系：

原参考椭球上的点P(B，L，H)，在辅助椭球上的坐标P(B，L，0)，则该点在辅助椭球上坐标的改正量分别为dB，dL，dH。根据文献[4]则有

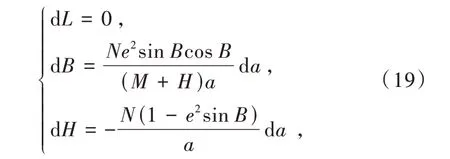
说明点P在辅助椭球中的经度值L没有发生改变，只有纬度值B和高程值H发生改变，设原参考椭球P1（B1，L1，H1），则点（B1，L1，Hm）在辅助椭球上，但其坐标系是在原参考椭球中。在辅助椭球上且也是辅助椭球坐标系的点为P′（B′1，L1，0），则有

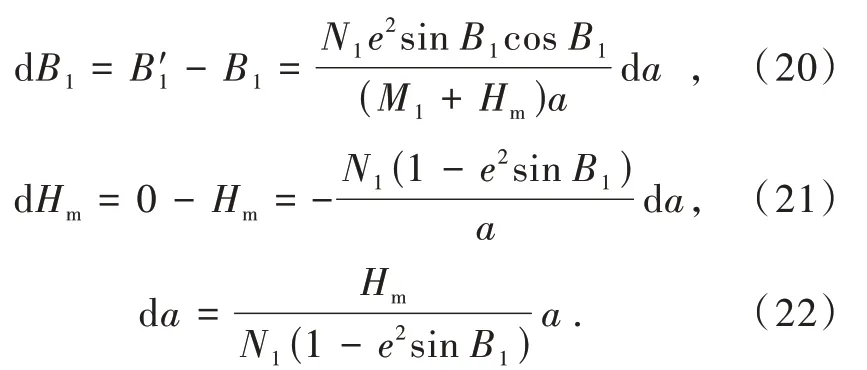
由式（17），（18）可得

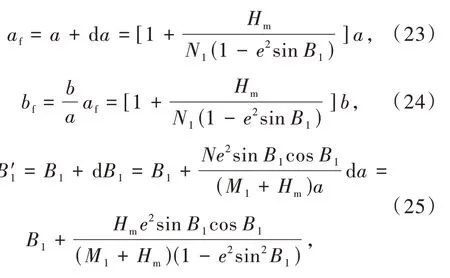
参考椭球P1（B1，L1，H1），在辅助椭球上的投影点P′（B′1，L1，0）是由辅助椭球的参考系坐标确定；参考椭球P2（B2，L2，H2）对应的辅助椭球上的点（B′1，L2，H′2）是在原参考椭球的坐标系，则其在辅助椭球上 的 投 影P′2（B′2，L2，0）是辅助椭球的参考系坐标确定。

3 顾及高程的Bowring 公式

在新构建的辅助椭球上应用Bowring 公式，其椭球的长短半轴随之变化，则辅助椭球的第二偏心率 为

由（B1，L1，H1），（B2，L2，H2）得到辅助椭球上的对应点（B′1，L1，0），（B′2，L2，0）带入到Bowring 反解公式（26）~（32）中，则有

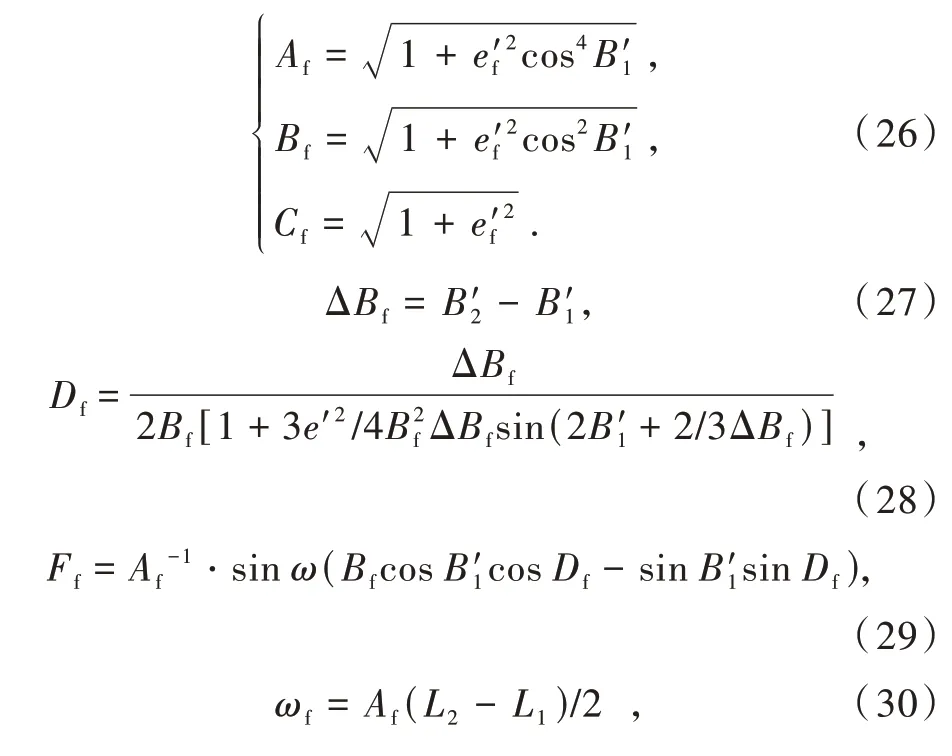
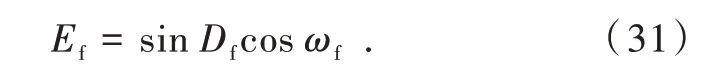
进一步带入求得顾及高程情况下的点P1，P2之间的距离以及两点之间的方位角为

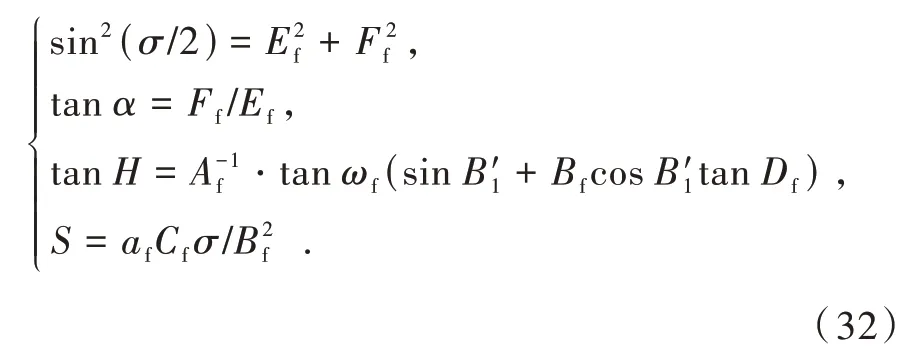
上述推导过程中，空间两点可以是任意两个具有高程差值的相邻规划航路点。可见在顾及航路点间高程值的情况下，Bowring 公式的推导过程较为简捷，比较适合计算机的编程实现。

4 算例分析

通过设计不同高程值时的相邻空间航路点间距离的算例[15]，进一步说明应用顾及高程的Bowring公式后对计算精度的影响。取克拉索夫斯基椭球基本常数a=6 378 245，e2= 0.006 693 421 622 97。计算Bowring 公式在是否顾及高程差时两点之间的大地距离及方位角见表1，相关差值对比见表2所示。

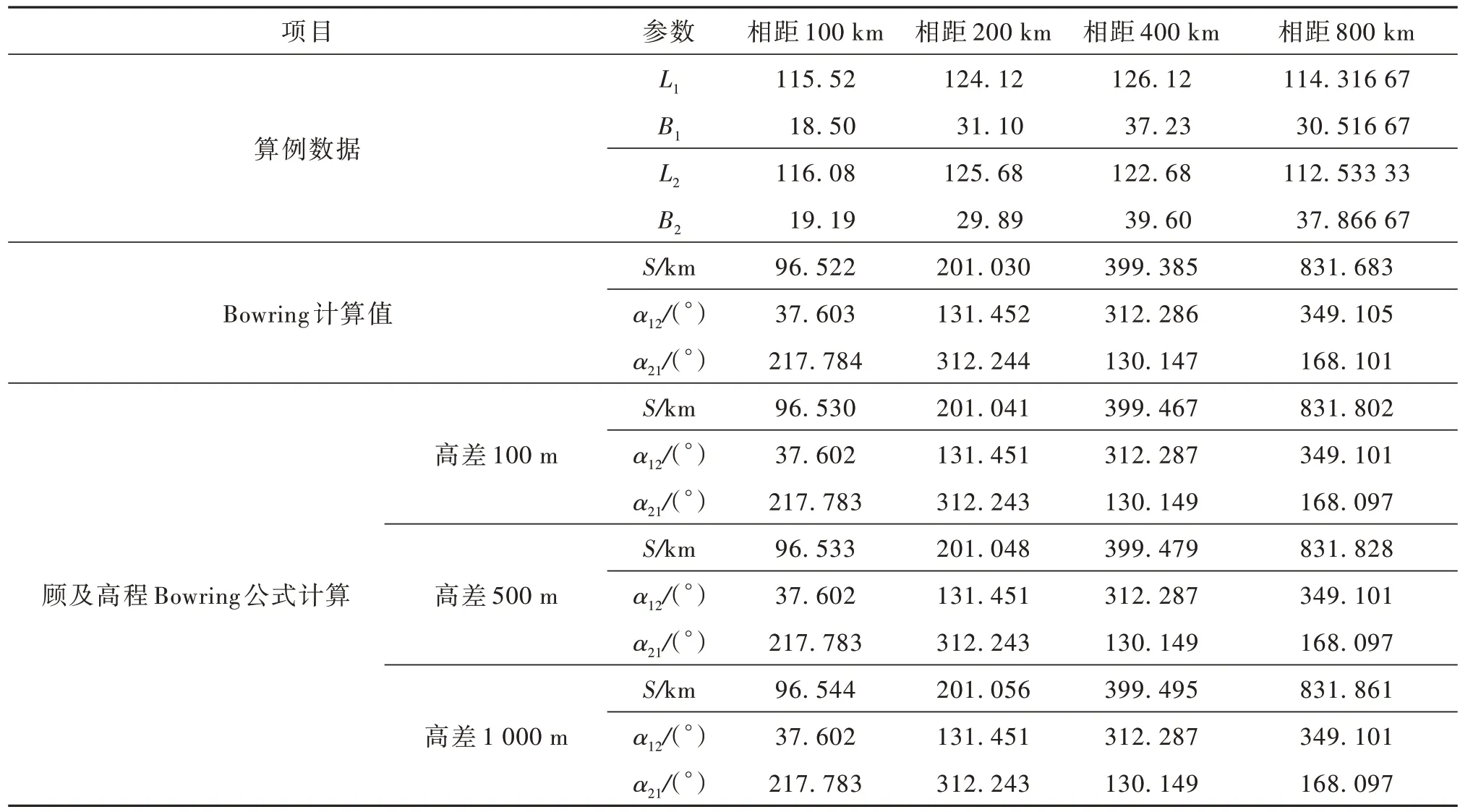
表1 空间两航路点间不同高程差值下的距离计算结果Table 1 Calculation results of distance between space waypoints with different elevation difference

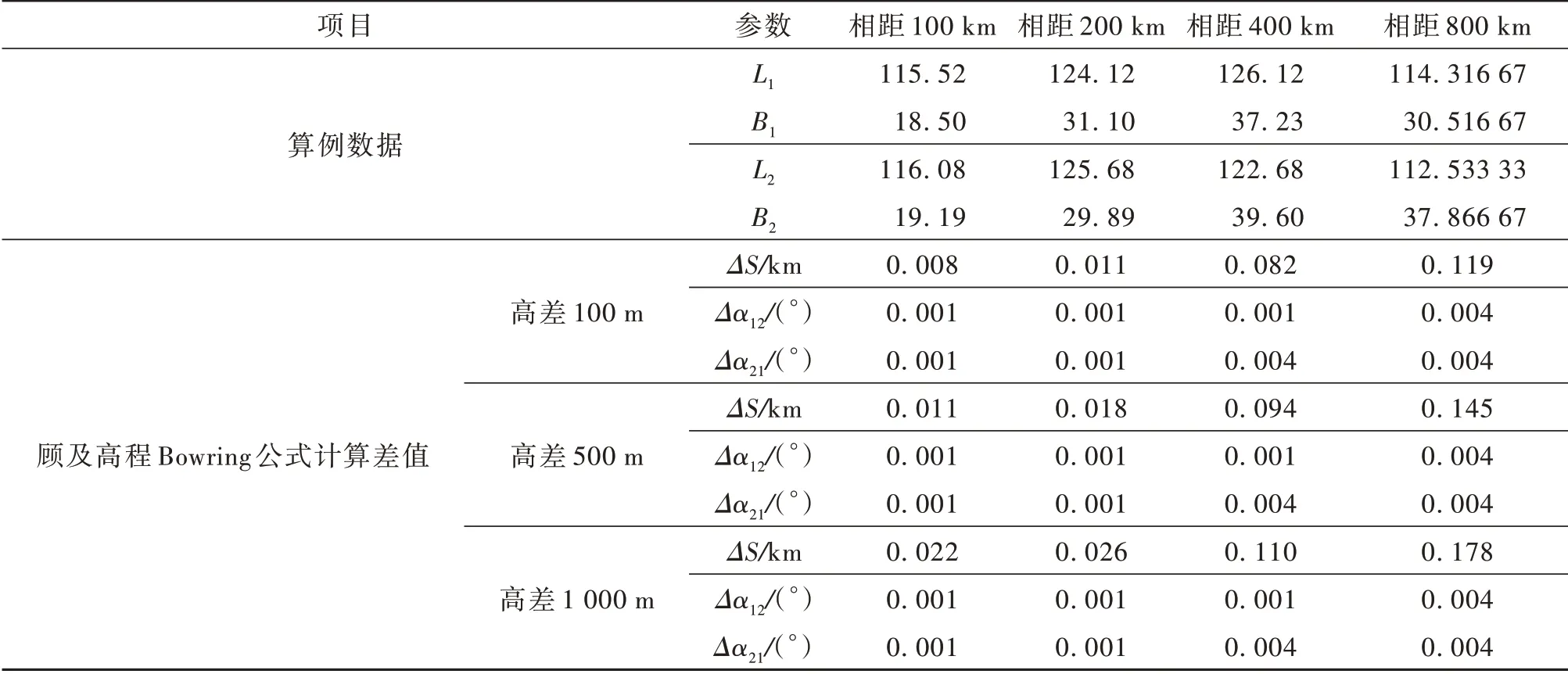
表2 空间两航路点间相关参数差值计算结果Table 2 Calculation results of correlation parameter difference between space waypoints

从表2 中数据可以看出，大地高程差值引起的距离差在中短距离（1 000 km 以下）的大地线长度中，从米级到百米级不等，说明高程的差值对于大地距离的计算精度有一定程度影响。在空间两点高程差值一定的情况下，两点间顾及高程与未顾及高程时的距离差值随着参考椭球面上的大地线长度的增加而增加。在空间两点经纬度不变的情况下，两点高程差值越大，则两点间的距离越大。而在两点方位角的变化中，高程差对两点之间的方位角的影响较小。在针对导弹由海面发射直接打击陆上目标时，需应用顾及高程的Bowring 公式求取大地线距离。而在导弹超低空临海巡航时，其航路点间的计算可以直接应用Bowring 公式，此时的距离也等效于导弹临海巡航时大圆航线的航程。

5 结束语

本文所给出的舰载对陆巡航导弹规划航路点间距离的计算方法，充分考虑了导弹由海上发射攻击陆地目标时规划航路点间可能存在一定高程差的特点。该算法较为简捷且精度符合需求，易于在规划舰载对陆巡航导弹航路的过程中快速计算航程，便于工程实现。