伺服系统速度环控制器参数的自整定及优化*

李方俊，王生捷

（北京机械设备研究所，北京 100854）

0 引言

由于较高的功率密度与稳定的输出转矩，以永磁同步电机为基础的交流伺服控制系统在工业生产中得到了广泛的应用。而速度环作为伺服控制系统中重要的中间控制环路，其决定了系统的响应速度与鲁棒能力，因此速度环控制器参数的设计影响着伺服系统的控制性能。常见的速度环自整定方法主要基于系统的数学模型，其中转动惯量直接决定了速度环控制器参数的大小，因此许多研究论文中速度环的控制器参数整定过程前常伴随着转动惯量的辨识过程。如文献［1］中采用改进加减速法对转动惯量进行辨识，克服了传统加减速法精度较差，负载惯量识别过程应用场景受限的缺点。文献［2］中利用朗道自适应的辨识算法对系统转动惯量进行辨识，并重点考量了噪声对辨识过程的影响。文献［3］利用扩展卡尔曼滤波器对永磁同步电机伺服系统的转动惯量辨识进行了仿真和实验研究，取得了较高的辨识精度。但以上方法存在调试参数较多，算法实现较为复杂的特点。本文希望转动惯量辨识算法实现简洁，试参数少，且对系统运动过程无特别要求，采用遗忘因子递推最小二乘法更加符合工程应用的需要［4-6］。

考虑到伺服系统本身具有诸多的非线性因素，建立的数学模型与实际系统不能完全匹配，辨识出的转动惯量仍包含有辨识误差，故在数学模型基础上整定出来的控制器参数往往并非最优结果，需要进一步的优化处理。如采用粒子群优化及其改进算法［7-8］，基于线性最优二次型调节器（linear qua⁃dratic regulator，LQR）方法等，对辨识出转动惯量后的控制器参数进行整定与优化［9］。

然而，智能寻优算法计算量大，且难以在MCU（micro control unit）中编程实现，基于模型的优化算法也依赖数学模型建立的精确性。

因此，本文提出一种基于转动惯量辨识的速度环控制器参数自整定及优化算法，即利用速度环数学模型，经频域分析推导出控制器参数后［10-11］，采用基于超调量和系统刚度的变步长迭代寻优算法，逐步完成对速度环控制器参数的整定和优化过程。此方法不依赖于系统的数学模型，且实现过程简单直观。通过仿真实验，证明了该方法的有效性。

1 速度环控制器参数设计

1.1 速度环控制器数学模型

交流伺服系统的控制器结构常由电流环、速度环和位置环构成，永磁同步电机作为其重要的执行单元，数学模型常表示为［12-13］

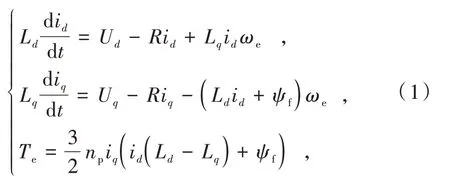
式中：Ld，Lq为d-q轴电感；R为电机电阻；Ud，Uq为电机d-q轴电压；id，iq为d-q轴电流；ψf为电机转子磁链；np为电机极对数；Te为电机电磁力矩；ωe为电机电角速度。对于表贴式永磁同步电机，系统常采用d轴参考电流指令= 0 的控制方式，故电机模型可简化为

因此交流伺服系统的电流环传递函数框图可表示为如图1 所示。

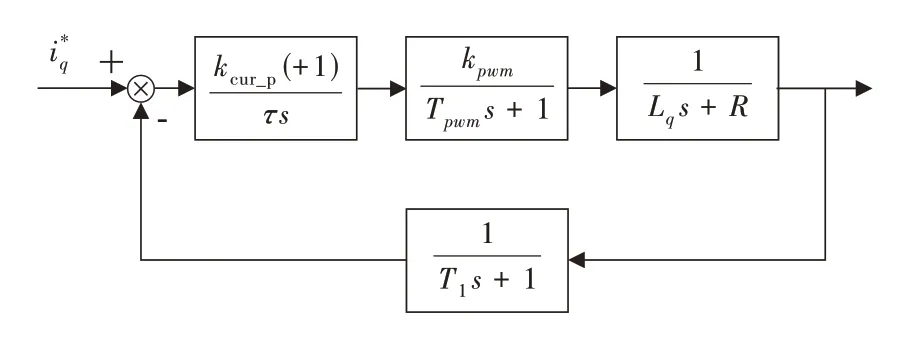
图1 电流环传递函数框图Fig.1 Block diagram of current loop transfer function

图1中kcur_p为电流环PI 控制器的比例系数；τ=kcur_p/kcur_i，kcur_i为电流环控制器的积分系数；kpwm为逆变器增益，Tpwm为逆变器延时时间常数；T1为电流环滤波系数，可将图1 中电流环开环传递函数表示为

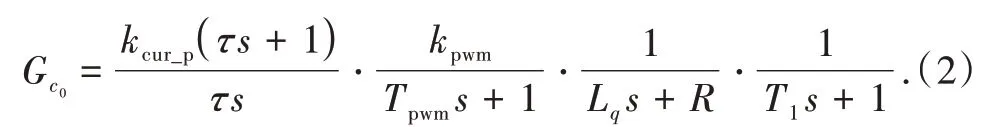
将式（3）合并后略去高阶项可简化为

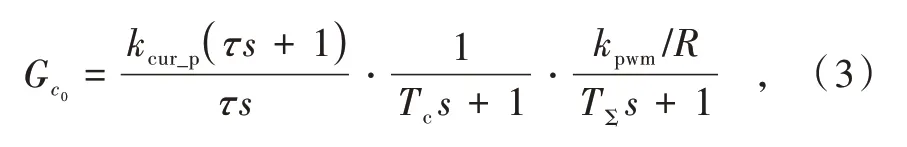
式中：Tc=Lq/R为电气时间常数；TΣ=Tpwm+T1，通常情况下电流环电气时间常数较大，故常采用控制器零极点对消的方式将电流环开环传递函数校正为I型系统，令

则校正后电流环开环传递函数为

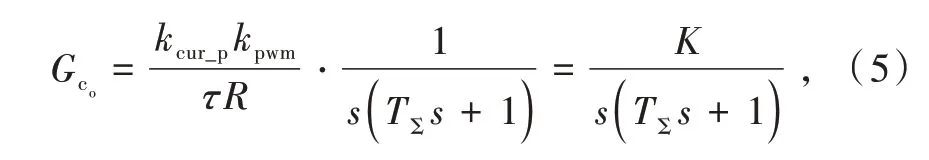
式中：K=kcur_pkpwmτR，其闭环传递函数可表示为

按照二阶系统最佳阻尼比K TΣ= 0.5，可得电流环控制器参数为［14-15］

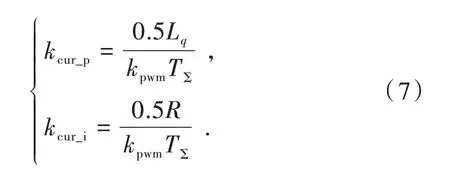
由于速度环的带宽远小于电流环的带宽，故在速度环内的电流环闭环传递函数可简化为

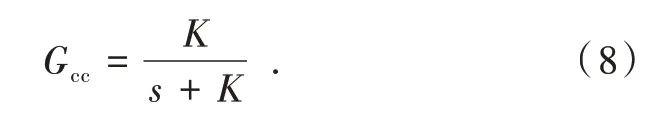
伺服系统的速度环传递函数框图可表示如图2所示。

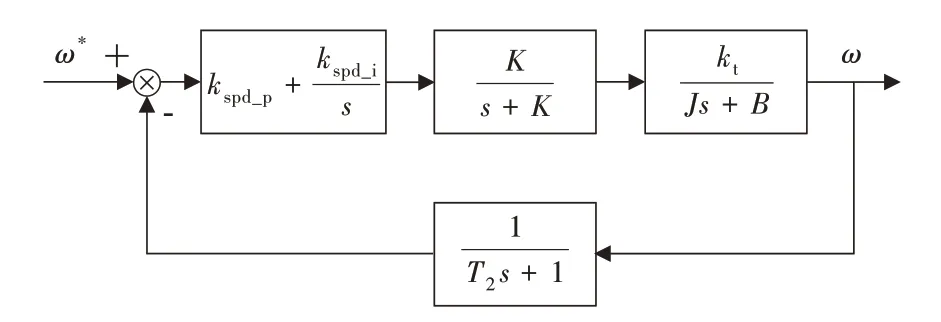
图2 速度环传递函数框图的Fig.2 Block diagram of speed loop transfer function

图2中，kspd_p，kspd_i为速度环控制器比例、积分增益系数；kt为电机力矩系数，J为电机端等效转动惯量，B为动摩擦因数，T2为速度环滤波系数，则转速环开环传递函数可表示为

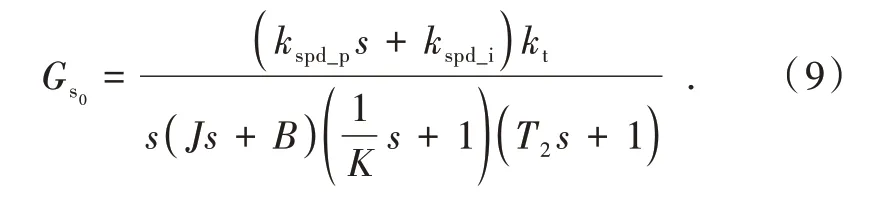
合并略去高阶项后可得

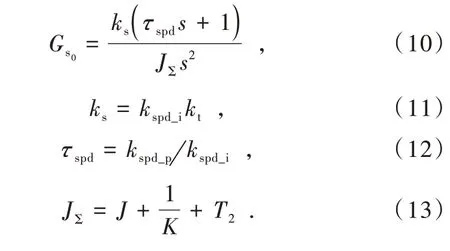
1.2 频域法设计速度环控制器参数

本文采用频域法分析速度环控制器参数的设计规则，在式（10）的基础上，设定速度环开环截止频率和相角裕度分别为ωsc，φss，可得到速度环的幅频特性和相频特性关系式为

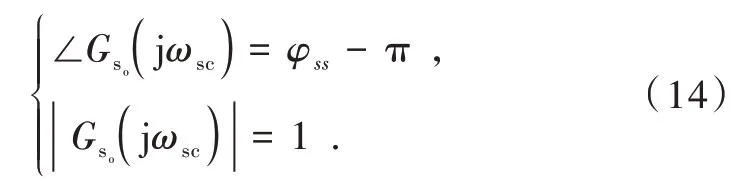
可计算得到

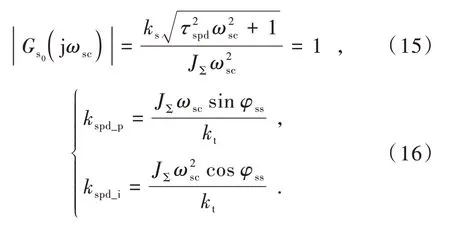
2 转动惯量辨识

从速度环控制器参数的设计规则可看出，欲完成自整定过程需已知系统电机轴端的等效转动惯量大小。本文采用遗忘因子递推最小二乘算法完成系统转动惯量的辨识过程。首先依据永磁同步电机的运动方程

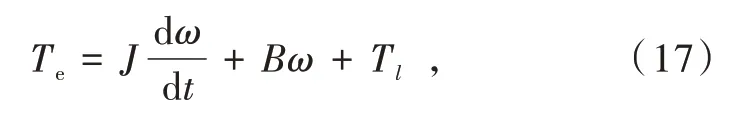
忽略掉动摩擦因数的影响，对式（17）进行离散化处理［16］：

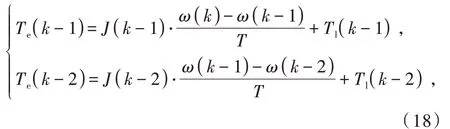
式中：k为采样时刻；T为采样周期。假设采样频率较高，系统在相邻2 个周期内的扰动力矩近似不变，根据（18）可得

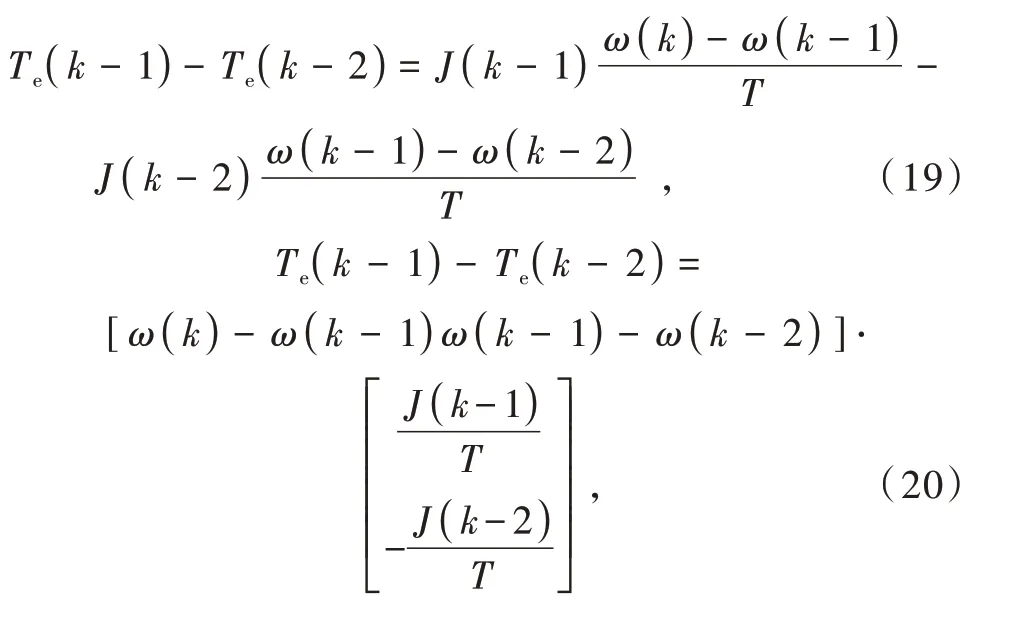
令

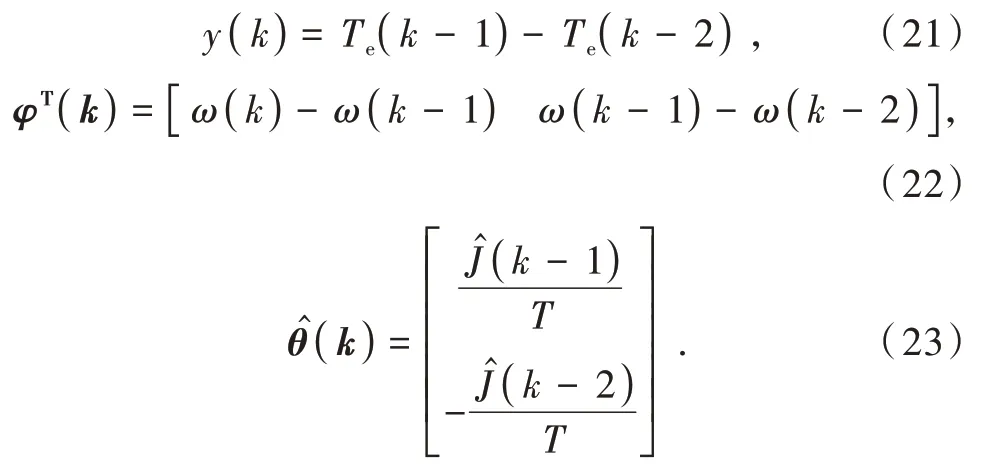
则可根据如下的遗忘因子递推最小二乘法完成转动惯量的辨识过程：

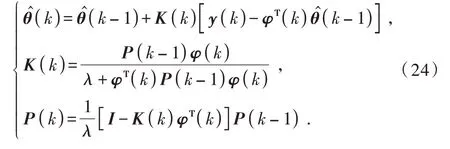
3 控制器参数寻优

将辨识出来的转动惯量代入式（16）后即可完成交流伺服系统速度环的自整定过程，但由于系统建模过程中的简化以及存在的未建模动态因素，因此自整定出来的速度环控制器参数往往并非最优的系统控制参数，需要对控制器参数进行优化处理。

本文设计了变步长迭代算法对系统的控制器参数进行优化处理，其流程图如图3 所示。图中kω1，kω2为速度波动的上下限系数，用于限制参数初始优化阶段时转速的调整范围，避免转速响应过大且为后续的转速调整保留余量；δ为速度反馈曲线的实际超调量，δspd为系统设置的超调量阈值。

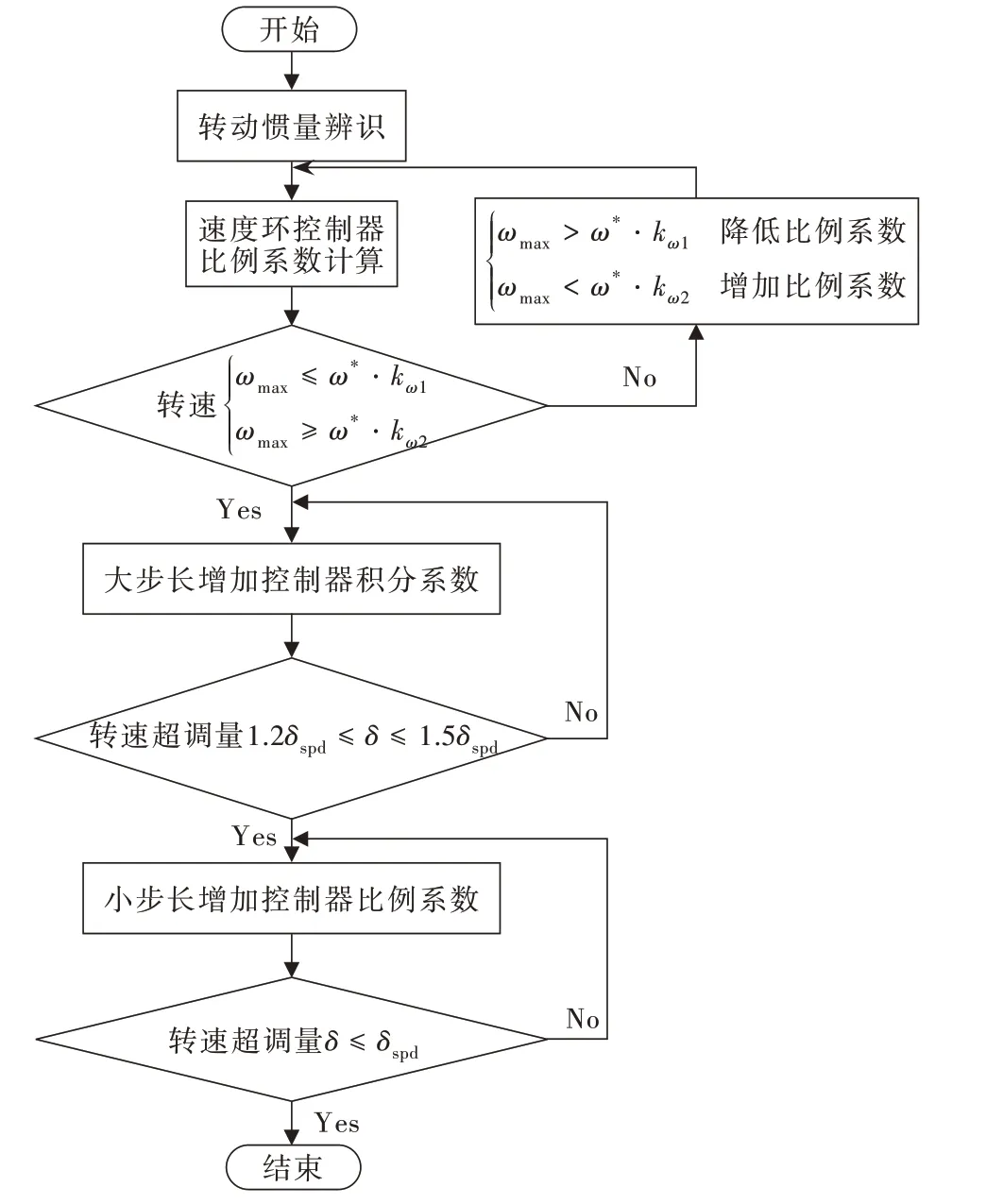
图3 迭代寻优算法流程图Fig.3 Procedural diagram of the iterative optimization algorithm

系统采用方波信号作为速度环的参考输入指令，参数优化流程如图4 所示。系统根据变步长迭代算法在转速信号到达期间，对速度响应超调量进行计算并优化控制器参数，下一个转速信号到来时进行下一轮迭代，直至得到满足要求的控制器参数。

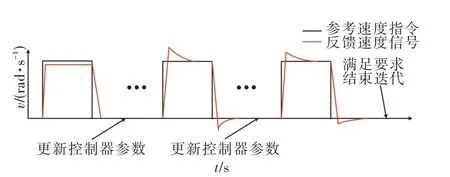
图4 参数优化过程Fig.4 Parameters optimization process

4 仿真结果及分析

本文针对所提出的算法在Matlab/Simulink 中进行仿真实验，所用永磁同步电机参数为：d-q轴电感Ld，q为6 mH，电 机 电 阻R为0.34 Ω，力 矩 系 数kt为0.579 N·m/A，电机转动转量J为0.05 kg. m2，摩擦因数B为0.01 N·m·s，额定转速为1 500 r/min；系统电流环控制周期为0.000 1 s，滤波系数为0.01，电流环控制器比例系数为0.3，积分系数为0.001 7。

首先在系统电流环工作条件下进行电机等效转动惯量的辨识实验，给定系统斜率为1 A/s 的斜坡电流指令信号，RLS 辨识模块中电流与转速的采样周期为0.000 5 s，遗忘因子λ为0.95，得到的转动惯量辨识曲线如图5 所示，大小为0.049 kg·m2，辨识误差为2%，辨识时间为0.4 s 左右。随后以2 倍大小变化系统的转动惯量，得到不同转动惯量下系统的辨识曲线如图6 所示。从图6 中可看出遗忘因子递推最小二乘法能准确辨识出系统的转动惯量，辨识时间长短与转动惯量的大小呈正相关关系。

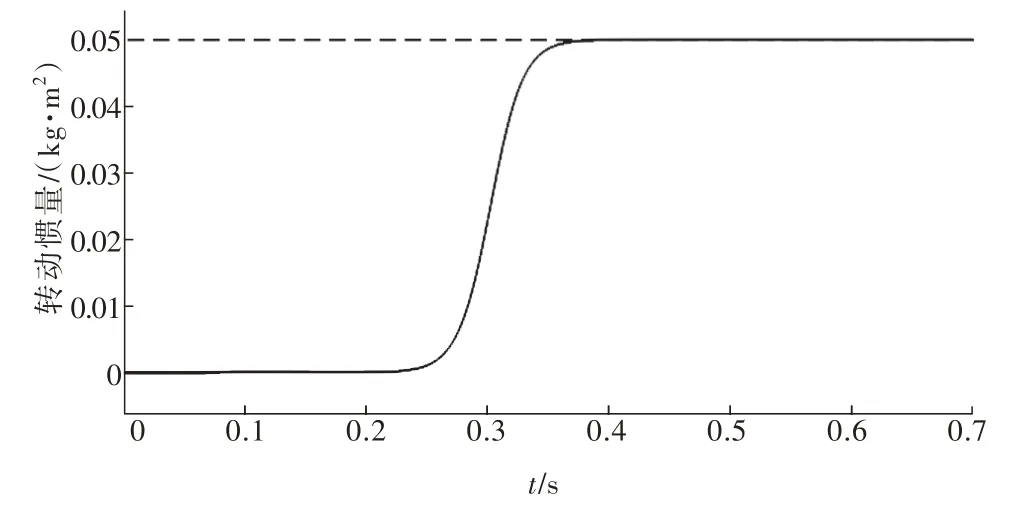
图5 转动惯量辨识Fig.5 Inertia identification

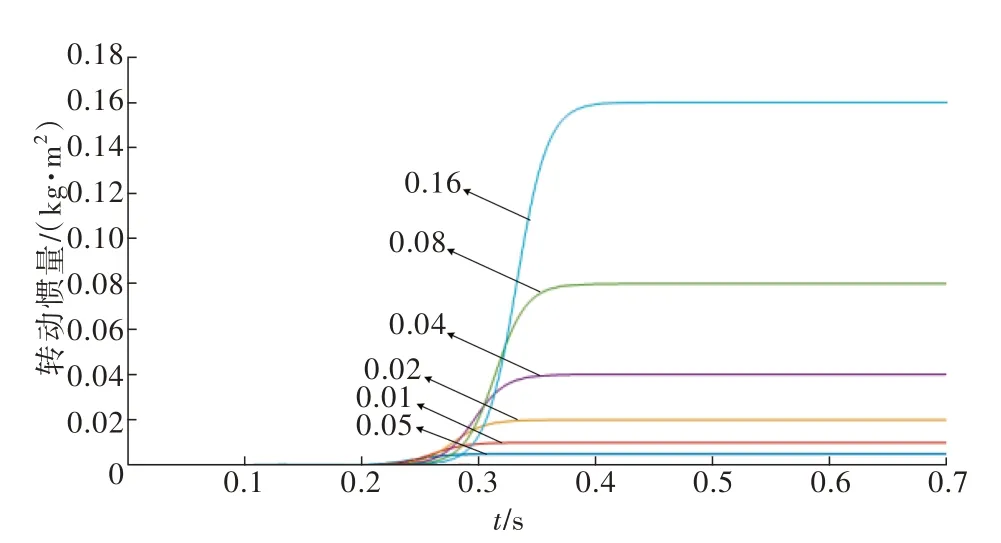
图6 变转动惯量辨识Fig.6 Variable inertia identification

依据辨识出的转动惯量即可开始速度环控制器参数的自整定过程。设定系统转动惯量为0.005 kg·m2，速度环开环频率为电流环开环频率的1/20，初始相角裕度按90°计算，计算可得速度环控制器自整定参数为：kspd_p= 0.423，kspd_i= 0，速度的上下限系数kω1，kω2为0.91和0.90。给定系统幅值为157 rad/s（约为电机额定转速）的方波速度指令后，得到的速度响应曲线如图7所示。由于转速上升过程中最大值为157 rad/s且存在小幅波动，说明比例系数设置偏大。为减小刚度和为后续比例系数的小范围调整留足余量，系统以步长0.01逐步减小比例系数，最终得到kspd_p= 0.16的转速曲线。过程中最大转速大小为141.7 rad/s 且变化平稳，稳态误差为15.7 rad/s。

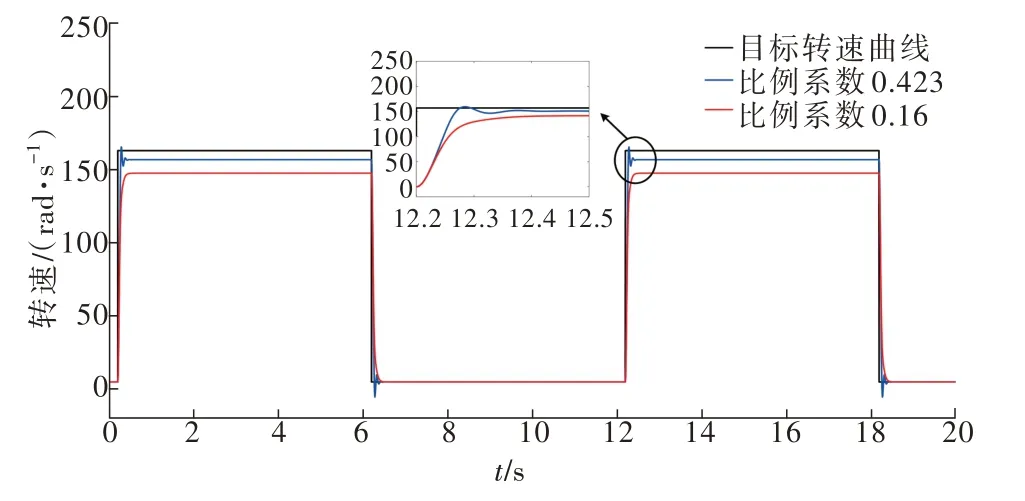
图7 比例系数初始标定Fig.7 Proportion gain initial setting

现保持比例系数kspd_p= 0.16 不变，目标转速为157 rad/s，以速度环采样周期（0.000 5 s）的10%为步长逐渐增加控制系积分系数，系统超调量阈值为5%，如图8 可以看到随着积分系数的增加，转速反馈曲线超调量增大，恢复稳态的调整时间变短；而比例系数的相对增加能压缩速度曲线的超调量，但会延长调整时间，且比例和积分系数大小同时影响着系统的刚度。表1 为上述积分系数调整过程中系统超调量的变化。

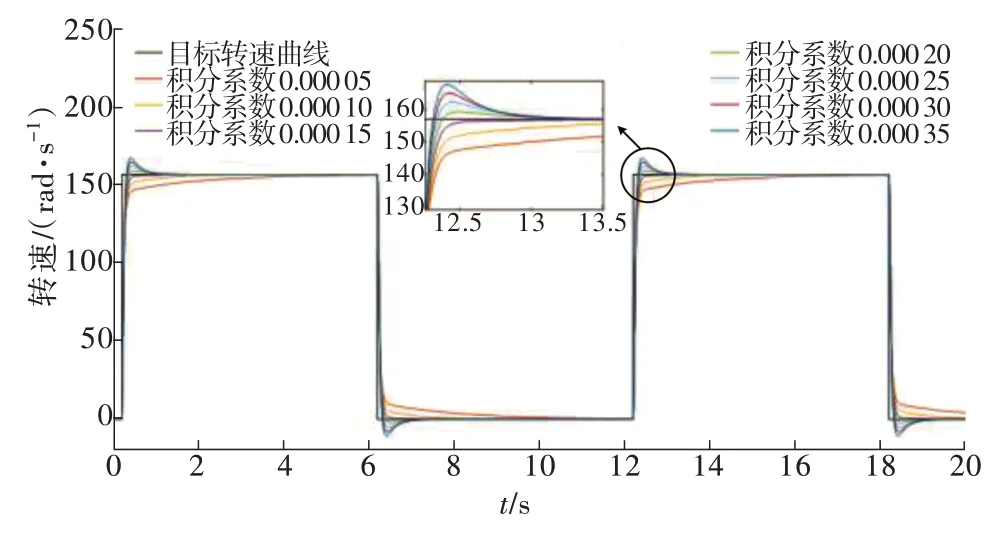
图8 积分系数调整Fig.8 Integral gain adjustment

表1 系统超调量变化Table1 System overshoot

针对如何调整系统的控制器参数使得转速曲线超调量合适，调整时间短，鲁棒性强，本文接下来采用小步长迭代寻优的算法寻找合适的控制器参数。以控制器参数kspd_p= 0.16，kspd_i= 0.000 35 为基准（系统超调量为6.3%），为了进一步增加系统的刚度和减小超调量，以当前比例系数大小的5%~10%（本文选取为0.01）为步长动态增加kspd_p，得到的曲线如图9 所示。直至系统超调量δ≤5%，此时比例系数kspd_p= 0.2，进一步增加比例系数会仍会增加系统的刚度，但过大的kspd_p会导致系统的调整时间延长，甚至引起系统的抖动，故目前得到的寻优参数kspd_p= 0.2，kspd_i= 0.000 35，既能保证系统的快速响应能力也能提高系统的鲁棒性。

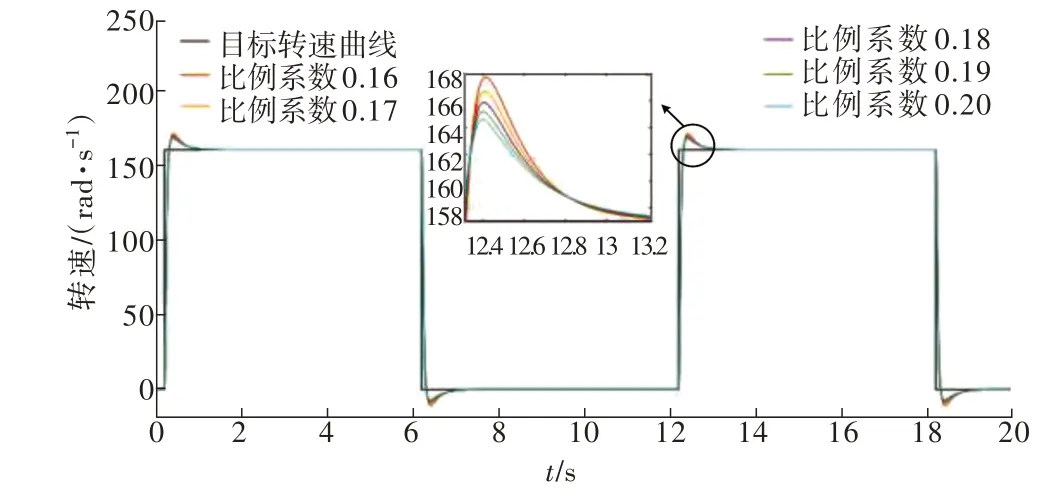
图9 比例系数调整Fig.9 Proportion gain adjustment

如图10 所示，为检验寻优参数的抗扰能力，给定系统157 rad/s 的阶跃转速指令信号，系统在10 s时施加大小为10 N·m 的扰动力矩，可得到如表2 所示的实验结果。从表中实验结果可看出，经过小步长迭代处理后的控制器参数抗扰能力增强，转速波动量大小相较于之前明显降低。

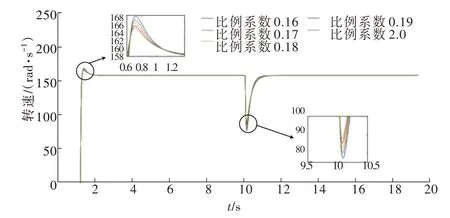
图10 系统加载测试Fig.10 System load test

表2 系统转速波动Table2 System speed fluctuation

5 结束语

本文针对交流伺服系统速度环控制器参数设计的需求，提出了一种基于转动惯量辨识的参数自整定及优化策略。仿真结果表明：遗忘因子递推最小二乘法能有效辨识出系统的转动惯量，为后续控制器参数初值的选取提供了参考。本文设计的变步长迭代寻优算法能有效完成控制器参数的整定及寻优过程，系统速度响应曲线超调量小，鲁棒性强，具有一定的工程实用性。