深度学习在解题教学中的应用

⦿甘肃省陇西县第二中学 张 博 张明远

1 引言

罗增儒教授认为：“对典型例题进行分析是提高解题能力的有效途径.”罗增儒教授总结了解题信息论、解题推理论、解题化简论、解题化归论、解题系统论、解题差异论和解题坐标系等解题理论.学习和运用这些理论指导解题实践，可以使学生对相应的例题、习题从不同角度分析和解答，从而实现深度学习.

成功解题的关键在于对题设进行合适的表征.不同的表征方式会使学生联想到不同的方法，从而引领不一样的解法；通过对不同解法的比较，让学生对数学知识和数学思想方法的理解更加深入本质，从而在这样的解题活动中积累数学活动经验，不断提升数学学科核心素养.

教者以一道较为经典的习题为例，以相关解题理论为指导，引领学生从例题呈现、题意分析、解法探究和解题反思四个方向对该题目进行深度学习，有效帮助学生拓宽解题思维、积累解题经验、提升解题能力、发展了核心素养.

2 例题呈现

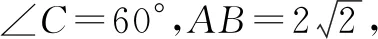
3 题意分析

3.1 画出图形，引进参数，整合信息

数形结合是解决数学问题的重要思想和方法，根据题目已有的信息，画出满足题目要求的图形，可以很好地帮助学生分析题设和结论，找到解题思路，提出解题方法.引进适当的参数，可以降低思考和分析的难度，简化解题的过程，有利于解题过程中解题信息的整合.

如图1，记BC=a，AC=b.

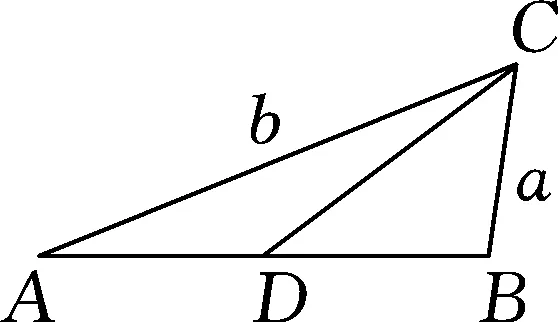
图1

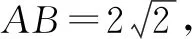
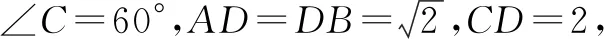
3.2 分析结论，联系题设，提出思路

解题的过程就是寻求题设和结论之间联系的过程，类似于过河，河的一边是条件，另一边是结论，解题思路就是过河的方法.通过对结论的分析，联系题设中的有关条件，就可以找到解决问题的思路和方法.

4 解法探究

4.1 将求△ABC面积的问题转化为计算ab的问题

生1：根据需要计算的ab，联系题设中已有的∠C=60°，联想到余弦定理，从而将问题转化为计算a2+b2.解答如下.

在△ABC中，由∠ADC+∠BDC=π，可得cos∠ADC+cos∠BDC=0.

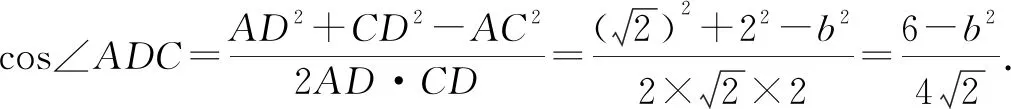
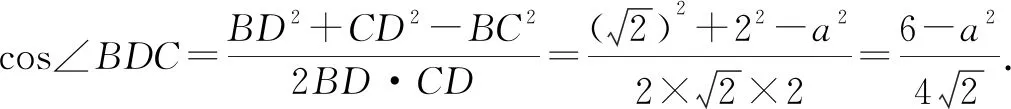
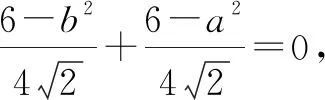
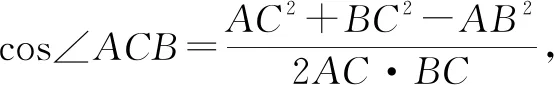
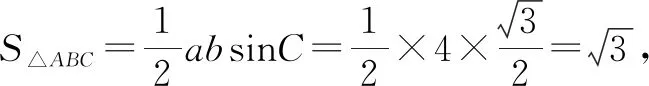
生2：根据需要计算的ab，联系题设中已有的∠C=60°，联想到平面向量的数量积，通过对向量式进行平方运算可以得到含a2,b2,ab的等式.解答如下.

a2+b2+ab=16.

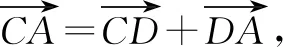
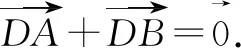
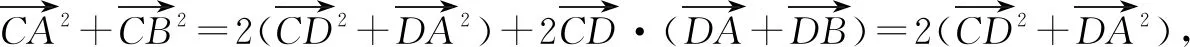
由a2+b2+ab=16，b2+a2=12可得ab=4.

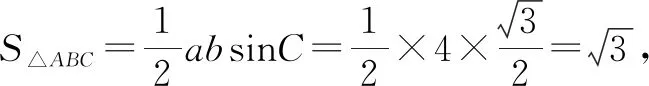
生3：根据需要计算的ab，联系题设中已有的∠C=60°，联想到余弦定理，从而将问题转化为计算a2+b2，再从a2+b2联想到三角形的中线长公式——阿波罗尼斯定理，解答如下.

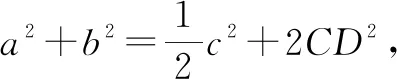
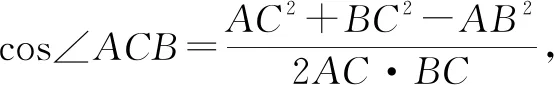
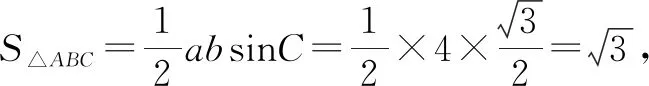
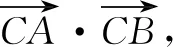
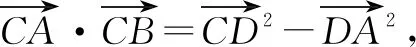
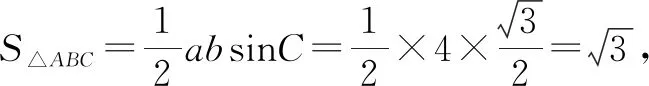
4.2 将求△ABC面积的问题转化为计算△ABC中AB边上高的问题

生5：通过建立平面直角坐标系，可以将求△ABC中AB边上高的问题转化为求点C纵坐标的问题，结合题设中的∠C=60°，联想到向量的数量积及其坐标运算，解答如下.

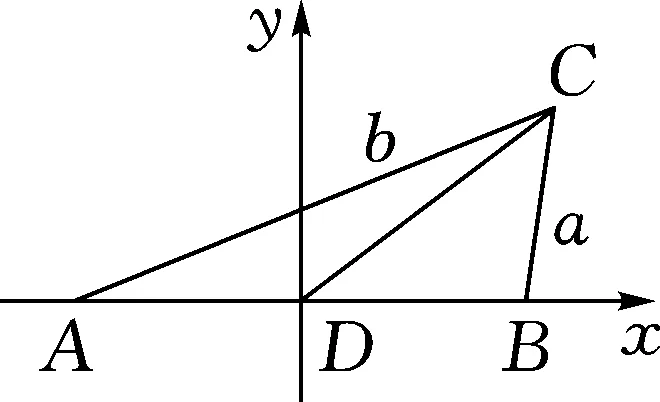
图2

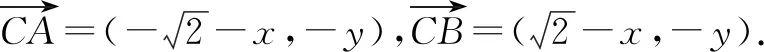
由CD=2，可得x2+y2=4.

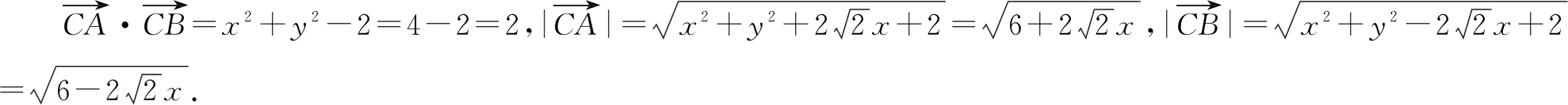
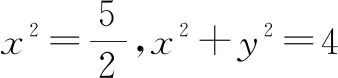
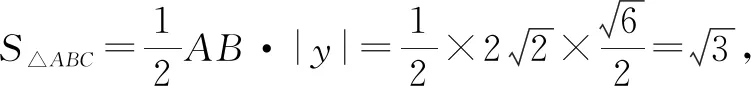
生6：与生5的解法类似，可以通过设角度，用三角函数来表示点C的坐标，解答如下.

设∠CDB=θ，由|CD|=2,得C(2cosθ,2sinθ).

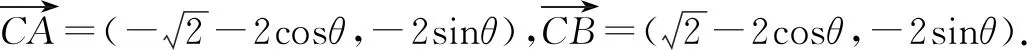
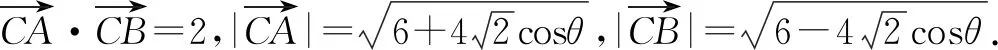
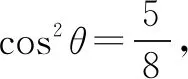
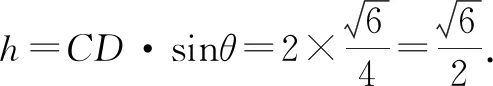
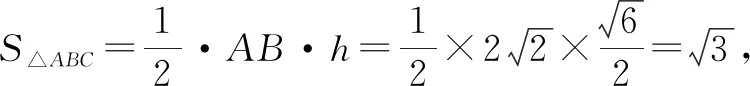
生7：由题设中的∠C=60°这一特殊角，联想到等边三角形，以AB为边构造等边三角形,可以发现∠AEB=∠ACB，从而联想到同弧所对的圆周角相等这一结论，进而借助等边三角形的外接圆解决问题.解答如下.

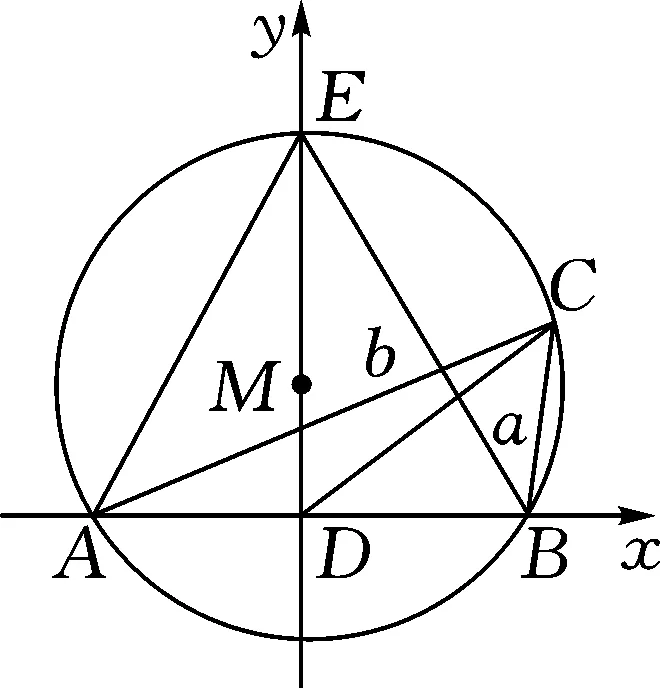
图3

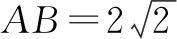
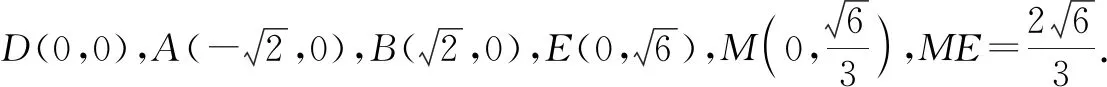
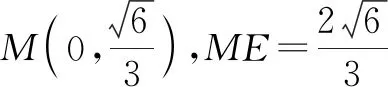
设∠CDB=θ，由CD=2得C(2cosθ,2sinθ).

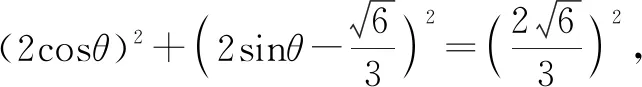
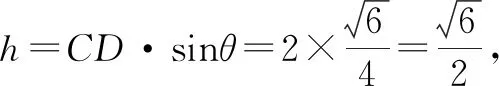
生8：在生7解法的基础上，将点C的坐标设为C(x0,y0)，解答如下.

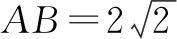
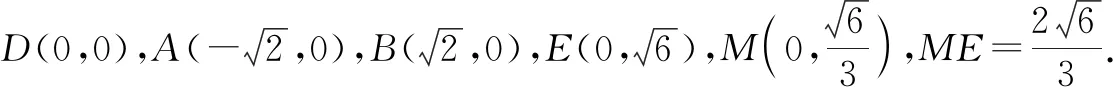
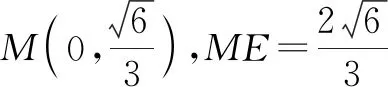
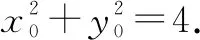
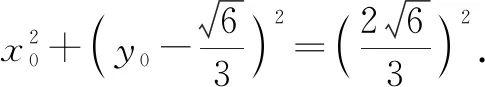
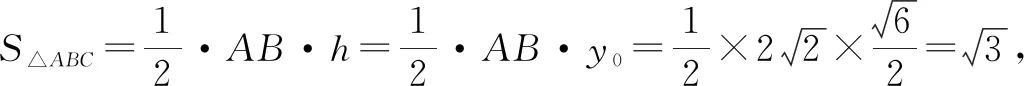
5 解题反思

通过多名学生不同解法的交流，打通了向量法、坐标法和余弦定理的联系，解题的过程就是从已知到未知的过程，其方法是多样的.不同的表征引发了不同的解法，不同的解法成就了经典习题.分析经典习题的解题过程，对比不同的解题思路和解题方法，让提升推理、运算素养水平落地生根并开花结果.

利用多元表征原理，分析经典习题的解题过程，研究解法，领悟奥妙，揭示本质，能够提高学生分析问题、解决问题的能力，有效培养学生逻辑推理和抽象思维能力.

借助经典习题，引导学生进行深度学习，让学生对数学知识的理解更加深入本质，让学生对数学思想和数学方法的认识更加全面深刻，从而积累解题经验，提升解题能力，发散解题思维.Z