研究高考真题 领悟命题立意 号准考向脉搏
⦿四川省双流中学(文卫星工作室) 曾月波 曹军才
1 引言
波利亚指出:解题的价值不是答案的本身,而在于弄清“是怎样想到这个解法的?”、“是什么促使你这样想,这样做的?”笔者以2021年普通高等学校招生全国统一考试理科数学甲卷第21题为例,从试题题型、背景、设问方式到问题解答多角度领悟命题立意,准确把握考向脉搏,突出思维导图在解题中的应用,不仅给出常规(通法)解法而且还给出简捷(秒杀)解法.
2 真题呈现

(1)当a=2时,求f(x)的单调区间;
(2)若曲线y=f(x)与直线y=1有且仅有两个交点,求a的取值范围.
3 试题分析
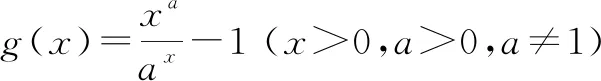
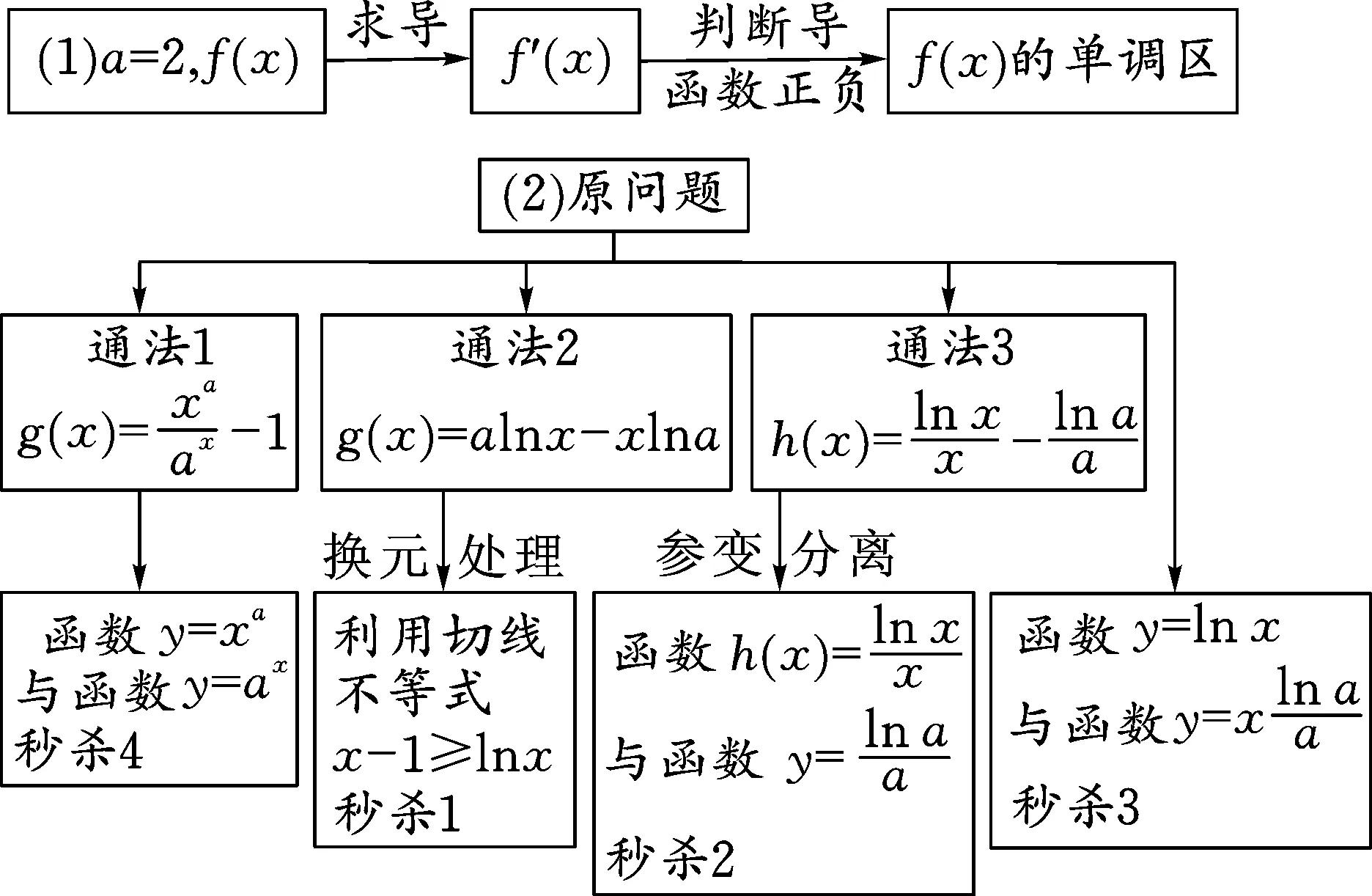
图1
4 试题解析
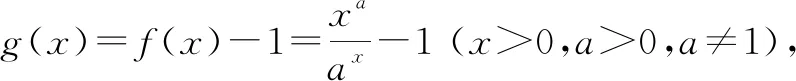


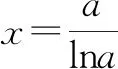
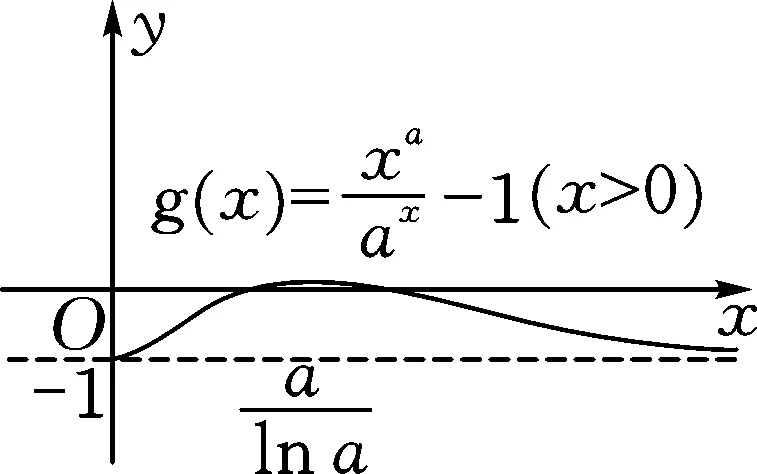
图2
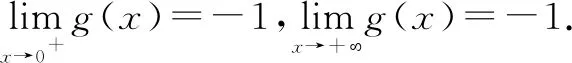
所以,如图2,要函数y=g(x)(x>0)有且仅有两个零点,必须且只需
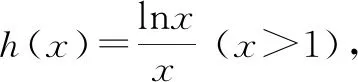
所以,当x∈(1,e)时,h′(x)>0,h(x)单调递增;当x∈(e,+∞)时,h′(x)<0,h(x)单调递减;
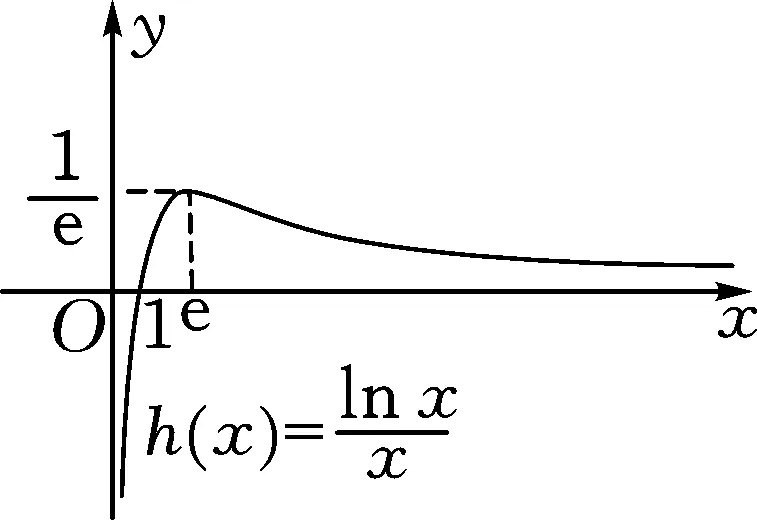
图3
当x=e时,h′(x)=0,h(x)取得极大值,最大值

即当a∈(1,e)∪(e,+∞)时,函数y=g(x)(x>0)有且仅有两个零点.
②当0
从而,函数y=g(x)在(0,+∞)上不可能有两个零点.
综上①、②,要曲线y=f(x)与直线y=1有且仅有两个交点,a的取值范围是(1,e)∪(e,+∞).
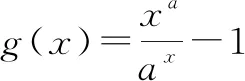
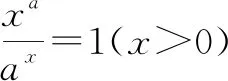
⟺方程xa=ax(x>0)有且仅有两解
⟺方程alnx=xlna(x>0)有且仅有两解.
设g(x)=alnx-xlna(x>0,a>0,a≠1),即等价于函数y=g(x)有且仅有两个零点.
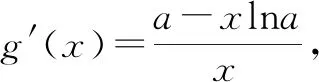
①当a>1时,


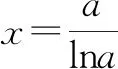

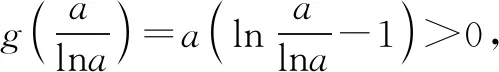
以下同通法1.

设r(t)=t-1-lnt(t>0),则
所以,当t∈(0,1)时,r′(t)<0,r(t)单调递减;
当t∈(1,+∞)时,r′(t)>0,r(t)单调递增.
因此r(t)的最小值为r(1)=0,所以不等式t-1-lnt>0的解集为(0,1)∪(1,+∞).
从而a的取值范围是(1,e)∪(e,+∞).
②当0
因此,函数y=g(x)在(0,+∞)上不可能有两个零点.
综上①、②,要曲线y=f(x)与直线y=1有且仅有两个交点,a的取值范围是(1,e)∪(e,+∞).
点评:通法2把原问题等价转化成函数g(x)=alnx-xlna的零点问题.多次转化,化归难度增加,同时运算能力要求也高,秒杀1利用换元法,进一步化归,把问题转化成以经典切线不等式x-1≥lnx为背景的问题,从而更易解决.同样还涉及到分类与整合、函数与方程、函数极限等数学思想.
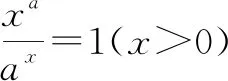
⟺方程xa=ax(x>0)有且仅有两解
⟺方程alnx=xlna(x>0)有且仅有两解
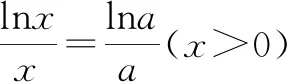
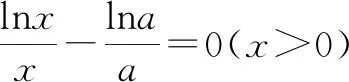
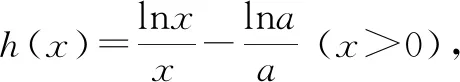
所以,当x∈(0,e)时,h′(x)>0,h(x)单调递增;
当x∈(e,+∞)时,h′(x)<0,h(x)单调递减;


当a∈(0,e)时,g′(a)<0,g(a)单调递减;
当a∈(e,+∞)时,g′(a)>0,g(a)单调递增;
当a=e时,g′(e)=0.

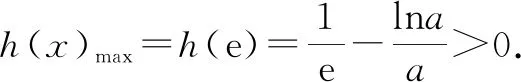
所以,h(x)在x∈(0,e)上有唯一零点;
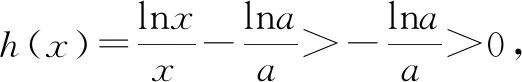
所以,当0 ②当1 图4 所以,当1 ③当a=e时, 所以,h(x)在(0,+∞)上有唯一零点,不合题意. ④当a>e时,当x∈(e,+∞)时,h(x)单调递减且h(a)=0,所以,h(x)在x∈(e,+∞)上有唯一零点; 当x∈(0,e)时,h(x)单调递增,且 图5 所以存在唯一x0∈(0,e),使得h(x0)=0. 即h(x)在x∈(0,e)上有唯一零点. 所以,当a>e时,h(x)在(0,+∞)上有两个零点,符合题意.(如图5) 综上所述,要曲线y=f(x)与直线y=1有且仅有两个交点,a的取值范围是(1,e)∪(e,+∞). ⟺方程xa=ax(x>0)有且仅有两解 ⟺方程alnx=xlna(x>0)有且仅有两解 所以,当x∈(0,e)时,h′(x)>0,h(x)单调递增; 当x∈(e,+∞)时,h′(x)>0,h(x)单调递减; 图6 秒杀法3:原问题 ⟺方程xa=ax(x>0)有且仅有两解 ⟺方程alnx=xlna(x>0)有且仅有两解 图7 以下同通法1. 本题初看函数结构新颖,细看实则熟悉,再做又感陌生;函数以幂函数为分子,指数函数为分母的分式型结构呈现,虽然两类函数背景熟悉,但以分式型结构呈现又觉新颖,又体现了高考命题的创新性.两个问题设置常规,难度呈现递进式有层次性,第(1)问起点低入手易,让基础薄弱的学生有成就感,充分体现了高考命题的基础性与人文关怀;第(2)问注重梯度,由“知识立意”到“能力立意”,凸显数学本质,让优秀学生能够脱颖而出,高考命题的综合性、应用性. 从题型角度而言,研究两函数图象交点(个数)的问题是常规题型,一般可以转化成研究相应方程根的问题,进而转化成研究函数的零点问题,常常涉及函数与方程、分类与整合、化归与转化、数形结合等数学思想.再观2021年文理科导数题,虽然函数模型不同、难度不同,但问题背景实则相同.Z

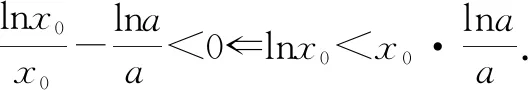
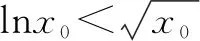

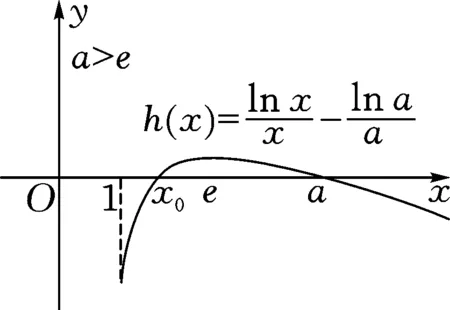


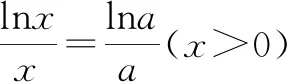
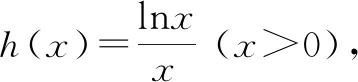
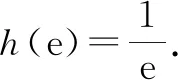
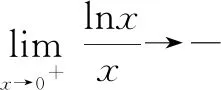

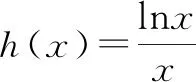





5 总结与感悟