热力管道热胀应力范围按不同标准计算的差异性探讨

匡江红， 余 斌

(1．上海工程技术大学 航空运输学院，上海 201620；2.上海市城市建设设计研究总院(集团)有限公司，上海 200125)

管道应力是指管道在内压、自重和其他外载荷作用下所产生的一次应力和在热膨胀、冷缩、位移受约束时所产生的二次应力[1-2]等，会影响管道安全使用，因此在管道设计时有必要进行应力验算。

金属材料因温差而形成热应力[3]，对于热力管道而言，运行时由热膨胀、冷缩所产生的热应力相对较大，较大的热应力有可能对管道、支架和设备造成损坏，严重时甚至造成人员伤害，影响正常运行[1-2]。目前，火力发电厂界区内热力管道由热态到冷态的热胀应力范围计算按照我国现行国家标准GB/T 32270—2015 《压力管道规范 动力管道》[4](以下简称动力管道国标)执行，与ASME B31.1—2020《ASME压力管道规范B31—动力管道》[5](Powerpiping，ASMEcodeforpressurepiping,B31，以下简称ASME标准)中关于热力管道热胀应力范围的计算公式有差异。在实际工程中，为了更好更全面地分析计算热胀应力范围，以确保管道运行安全，需要了解采用不同标准计算的结果差异，并对差异进行一定的分析。因此，笔者以3个简单管系为例，根据上述2个标准给出的计算公式，采用力法计算了热力管道热胀应力范围，并对计算结果进行对比分析。

1 不同标准中热胀应力范围的计算公式

1.1 动力管道国标中热胀应力范围的计算公式

热胀应力范围是指管道由于热胀、冷缩等变形受约束而产生的应力。动力管道国标中，管系由热膨胀、端点附加位移等荷载所产生的管系热胀应力范围σE计算公式为：

(1)

式中：σE为热胀应力范围，MPa；Mc为按热膨胀、端点附加位移等荷载和钢材在20 ℃的弹性模量计算的热胀合成力矩范围，N·mm；W为管道截面模量，mm3；i为应力增大系数。

对于直管和弯管，热胀合成力矩范围Mc计算公式为：

(2)

式中：Mx、My、Mz分别为管道由于热胀、冷缩等变形受约束而产生的力矩在x、y、z3个方向上的分量，N·mm。

1.2 ASME标准中热胀应力范围的计算公式

而在ASME标准中，管系热胀应力范围σE的计算公式为：

(3)

式中：Fa为管道热胀、冷缩时由位移应变产生的轴向力，N；Ap为管道截面积，mm2；ia为轴向应力增大系数，对于直管及弯管段ia取1.0；Mi为管道热胀、冷缩时平面内的弯矩，N·mm；Mo为管道热胀、冷缩时平面外的弯矩，N·mm；Mt为管道热胀、冷缩时由位移应变产生的扭矩，N·mm；Z为管道截面模量(相当于式(1)中的W)，mm3；ii为平面内应力增大系数；io为平面外应力增大系数；it为扭矩应力增大系数，各应力增大系数具体取值方法见ASME B31J—2017 《ASME 压力管道规范 B31—金属管道构件的应力强化因子(i因子)、弹性因子(k因子)及其测定》[6](stressintensificationfactors(i-factors)flexibilityfactors(k-factors),andtheirdeterminationformetallicpipingcomponents，ASMEcodeforPressurePiping,B31)。

式(3)等号右边根号内第一项为由位移应变产生的轴向应力范围项，第二项为由位移应变产生的弯曲应力范围项，第三项为2倍的由位移应变产生的扭矩应力范围项。

2 不同标准热胀应力范围实例计算

目前,针对热胀应力范围的计算方法较多，有力法、位移法、等值刚度法和有限元法[7]等，为了便于对热胀应力范围进行计算分析，针对较简单的管系，采用力法计算较为直观方便。

2.1 热胀应力范围的力法计算原理

对A、B两端固定的管系，将末端B释放，管系自由舒展后由超静定管系变为静定管系，末端B移到自由位置成为自由端B′，在自由端施加复原力PB(包括力FB和力矩MB)，使自由端B′复原到未释放前的末端B。

力法需要求解的是复原力PB，可根据卡氏第二定理求解得到[7]。卡氏第二定理指出，在外力PB的作用下，弹性体上PB作用点在作用方向的位移等于该管系位能U对该点外力PB的偏导数。管系位能U为作用在管系各点的垂直于管道的2个相互垂直方向的弯矩Mb、Mb′，沿管道的扭矩Mt，以及轴向力Fn(相当于式(3)中Fa)和2个相互垂直方向的剪切力Fs及Fs′产生的变形能之和：

(4)

式中：E为材料的弹性模量，MPa；J为管道截面惯性矩，mm4；k为弯管柔性系数；l为管长，mm；A为管道截面积，mm2。

对U求力FB的偏导数，得到位移δB如下：

(5)

同理，对U求力矩MB的偏导数，得到角位移θB：

(6)

根据管系中管件的空间角度以及其与坐标轴的投影关系，将弯矩、扭矩展开为3个方向力矩的表达式，将轴向力和剪切力展开为3个方向力的表达式。通过推导，可得到与空间几何有关的变形系数矩阵H与复原力PB和位移δθB之间的关系：

HPB=δθB

(7)

其中，

式中：FBx、FBy、FBz为力FB在坐标系x、y、z3个方向上的分量；MBx、MBy、MBz为力矩MB在坐标系x、y、z3个方向上的分量；Δx、Δy、Δz为管系末端B的位移δB在x、y、z3个方向上的分量;Δθx、Δθy、Δθz为管系末端B的角位移θB在x、y、z3个方向上的分量。

根据6个未知量、6个变位方程可以求解得到复原力PB。首先根据管系中直管、弯管所在空间位置，计算出矩阵H的36个系数;再根据管道热胀工况，计算出管系从热态到冷态的位移变化范围，从而得到复原力PB的变化范围。对简单管系来说，这一求解过程一般可通过手算完成。

得到复原力PB的变化范围后，可以由静力平衡方程来求解管系中的管段在计算点截面的内力(力矩)的变化范围。

由于管系末端B得到释放，AB管段变为悬臂管道，计算截面j上x、y和z方向的力矩可以由悬臂B端面到j截面所有的力分别对j截面在x、y和z方向的力矩累加求得[7]。作用力的计算公式可以根据力(力矩)平衡得到。为便于实例计算分析，管段不考虑支吊架、重力等外力作用，管系任一截面j的内力(力矩)变化范围(复原力点B到计算截面j)的计算可简化为式(8)。

(8)

式中：Xj、Yj、Zj为直角坐标系中截面j相对于复原力作用点B的坐标；Fxj、Fyj、Fzj和Mxj、Myj、Mzj分别为管系中的管段(复原力点B到计算截面j)在计算点截面的内力和力矩的变化范围。由此可得出任一管段在截面j处的x、y、z方向作用力和力矩的变化范围。

2.2 实例计算

以3个简单管系为例，按照力法和2个标准给出的计算公式进行计算，得到热胀应力范围并进行对比分析。计算实例中，管系两端固定，没有端点附加位移。管系中间无支吊架，不考虑施加除重力外的力。在评估从热态到冷态的热胀应力范围计算时，重力影响会抵消，因此在计算热胀应力范围时仅考虑热态工况到冷态工况间温度变化引起的位移变化。

2.2.1 单一直管热胀应力范围

算例一是两端固定的单一直管，示意图见图1。假设蒸汽管道外径为219 mm，壁厚为6 mm，长度为5 m，材料为20号碳钢，工作压力为1.6 MPa，工作温度为200 ℃(线性膨胀系数α=12.1×10-6K-1，弹性模量E=17.6×104MPa)[8]，冷态温度为20 ℃(α=11.2×10-6K-1，E=19.8×104MPa)。计算得到复原力仅有轴向力，变化范围为1 731 kN。

图1 两端固定的直管

按照动力管道国标，得到热胀应力范围为0 MPa；按照ASME标准，得到热胀应力范围则为431 MPa，即为轴向应力范围，该值超过一定值时会导致管道材料塑性变形，影响管道的安全使用。显然，当轴向力占主导时，轴向应力不能忽略。

2.2.2 两端固定的L形管系的热胀应力范围

算例二是平面内两端固定的L形管系，示意图见图2。由于平面内的管系不产生扭矩，可以分析不含扭矩的热胀应力范围差异。假设除管道布置外，其他同算例一，直管1沿x轴长度为2.7 m；接弯头2，半径为300 mm，壁厚与直管相同；再接y轴方向直管3，长度为3.7 m。

图2 xy直角坐标平面的L形管系

表1给出了L形管系中各管段计算点截面处从热态到冷态的力和力矩变化范围。表2给出了L形管系按照2个标准计算得到的从热态到冷态的热胀应力范围对比。

从表1和表2可以看出，按照ASME标准计算得到的各节点热胀应力范围值均比按照动力管道国标计算得到的值稍大，原因是ASME标准计算公式中增加了轴向力项。

表1 L形管系中各计算点截面处从热态到冷态的力和力矩变化范围

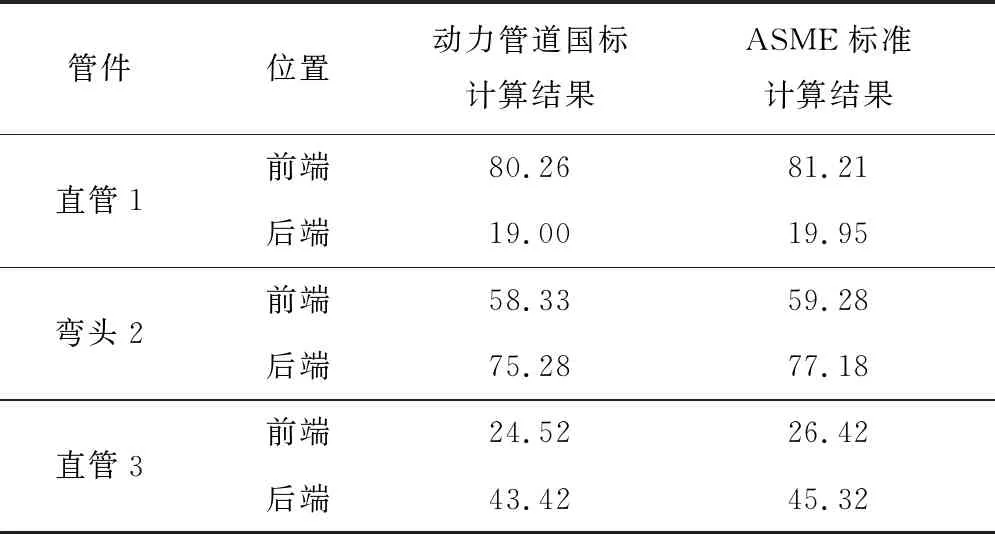
表2 L形管系热胀应力范围的计算结果对比

2.2.3 Z形空间管系热胀应力范围

算例三是两端固定的Z形空间管系，示意图见图3。空间管系会产生扭矩，可以分析考虑扭矩的热胀应力范围差异。假设除管道布置外，其他同算例二，管系布置如下：直管1沿x轴长度为2.7 m；接xy平面内弯头2，半径为300 mm；再接y轴方向直管3，长度为3.4 m；直管3末端接yz平面内弯头4，半径为300 mm；再沿z轴接直管5，长度为2.7 m。

图3 直角坐标系内的Z形空间管系

表3给出了Z形空间管系中各管段计算点截面处从热态到冷态的力和力矩变化范围。表4给出了Z形空间管系按照2个标准计算得到的从热态到冷态的热胀应力范围对比。

从表3和表4可以看出，按照ASME标准计算得到的直管的热胀应力范围值均比按照动力管道国标计算得到的热胀应力范围值稍大，而弯管的计算值则相反，初步判断是扭矩影响的结果。

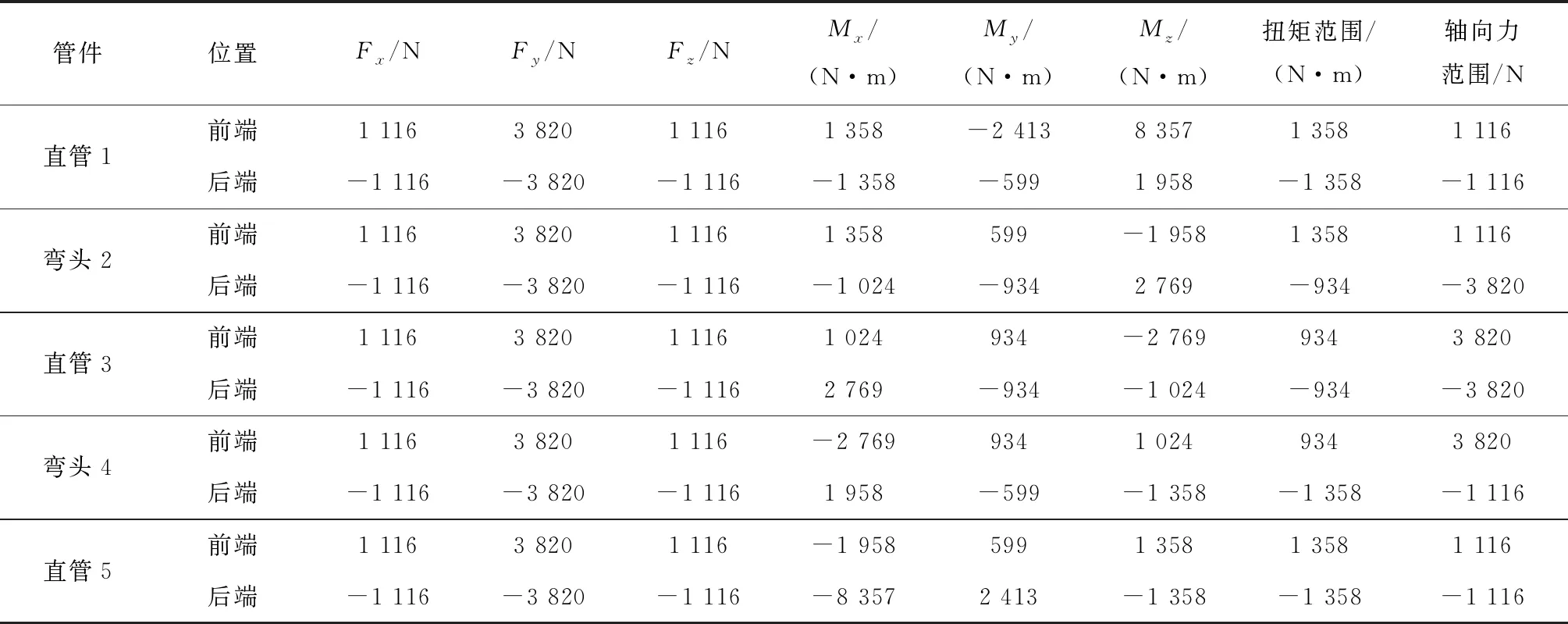
表3 Z形空间管系中各计算点截面处从热态到冷态的力和力矩变化范围

表4 Z形空间管系热胀应力范围的计算结果对比

3 不同标准计算的热胀应力差异分析

3.1 直管段计算值的差异分析

首先分析算例二和算例三的直管段，对直管1的后端点进行分析，其弯矩和扭矩为：

Mi=Mz

(9)

Mt=Mx

(10)

Mo=My

(11)

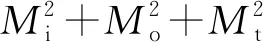
3.2 弯管段计算值的差异分析

对于弯管，根据ASME标准引用的ASME B31J—2017中应力增大系数相关参数，io=0.75ii/0.9，it=1.0。ASME标准弯管的ii与动力管道国标中的i取值相同。

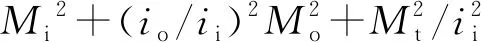
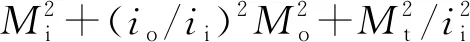
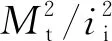
4 结 语

采用不同标准以3个简单管系为例,对发电厂界区内热力管道的热胀应力范围进行了计算。计算结果表明，对于平面管系和空间管系的直管段，由于ASME标准中热胀应力计算公式中增加了轴向力项，各节点热胀应力范围值均比按照动力管道国标计算结果的值要大;但对于空间管系的弯管部分，由于扭矩的影响，则有可能相反。考虑到案例不可能穷尽，在轴向力占比较大时或其他原因，也会出现弯管按照ASME标准计算得到的热胀应力范围值大于动力管道国标计算结果的可能性。

在实际工程中，应留意直管的热胀应力范围增大的情况，同时关注除直管外其他管件按不同规范计算的差异，合理分析热胀应力范围的大小变化。