SCR脱硝系统的强化学习复合串级控制
陈皓炜, 贾新春, 孙小明, 侯鹏飞
(山西大学 自动化与软件学院,太原 030013)
火电机组运行过程中会产生NOx、粉尘等污染物,对环境造成不同程度的危害。随着我国相关政策的发布以及对大气污染物排放要求的日趋严格[1],对火电机组进行超低排放改造已经刻不容缓。目前,由于成本低、效率高、运行可靠等优点,选择性催化还原(SCR)技术在工业现场应用广泛,已经成为一项成熟的技术。近年来,虽然在脱硝系统喷氨量控制方面已有大量的研究,但其仍有很大的改进空间。赵海涛等[2]采用神经网络优化比例积分微分(PID)参数来控制SCR脱硝系统,与传统PID相比抗干扰性能更好,适应能力更强。白建云等[3]将多模型切换串级控制器用于脱硝系统的控制中,实验表明该方法的鲁棒性好,更加适合变工况的工业过程控制。邢波涛等[4]将神经网络与动态矩阵控制算法相结合对SCR喷氨量进行控制,结果显示该算法有更小的波动和更好的控制性能。李健等[5]对线性自抗扰控制进行改进并结合了扩张状态观测器,在脱硝系统仿真中取得了满意的控制效果。
近年来机器学习受到了越来越多学者的关注,其中强化学习策略已成为控制领域的热点,已广泛应用于机器人控制[6]、游戏控制[7]、自动驾驶控制[8]等领域。强化学习可以与周围环境进行互动反馈并对环境产生影响,因此也可以应用到工业过程控制中[9]。在SCR脱硝系统控制方面强化学习的应用较少,PID的应用较多,然而传统的PID控制在应对脱硝环境多扰动、大惯性等特性时无法取得满意的控制效果。
针对上述问题,笔者提出一种改进的双延迟深度确定性策略梯度(ITD3)-比例积分(PI)复合串级控制方法并将其用于SCR脱硝系统控制中。首先,借鉴PID控制思想提出了一种ITD3算法,通过对出口NOx质量浓度设定值与测量值之间的误差进行微分和积分运算生成新的环境状态,并将新的状态与测量值、误差同时储存在经验池中;然后,利用扰动观测器(DOB)来估计脱硝过程的扰动,并进行前馈补偿;最后,对所提出的方法进行仿真对比实验。该方法为强化学习在脱硝系统喷氨量控制中的应用提供了借鉴。
1 SCR脱硝系统复合串级控制
1.1 SCR脱硝技术
SCR烟气脱硝是火电机组中最常见的一种脱硝工艺方法。脱硝反应所需温度一般在300~600 ℃,液氨储罐中的液氨经过氨蒸发器形成氨气储存于氨缓存器中,氨缓存器中的氨气与空气混合后经喷氨格栅进入烟道,氨气和NOx在催化剂(一般为V2O5/TiO2)的作用下转化为氮气和水。图1为SCR脱硝系统在正常情况下的工艺流程。
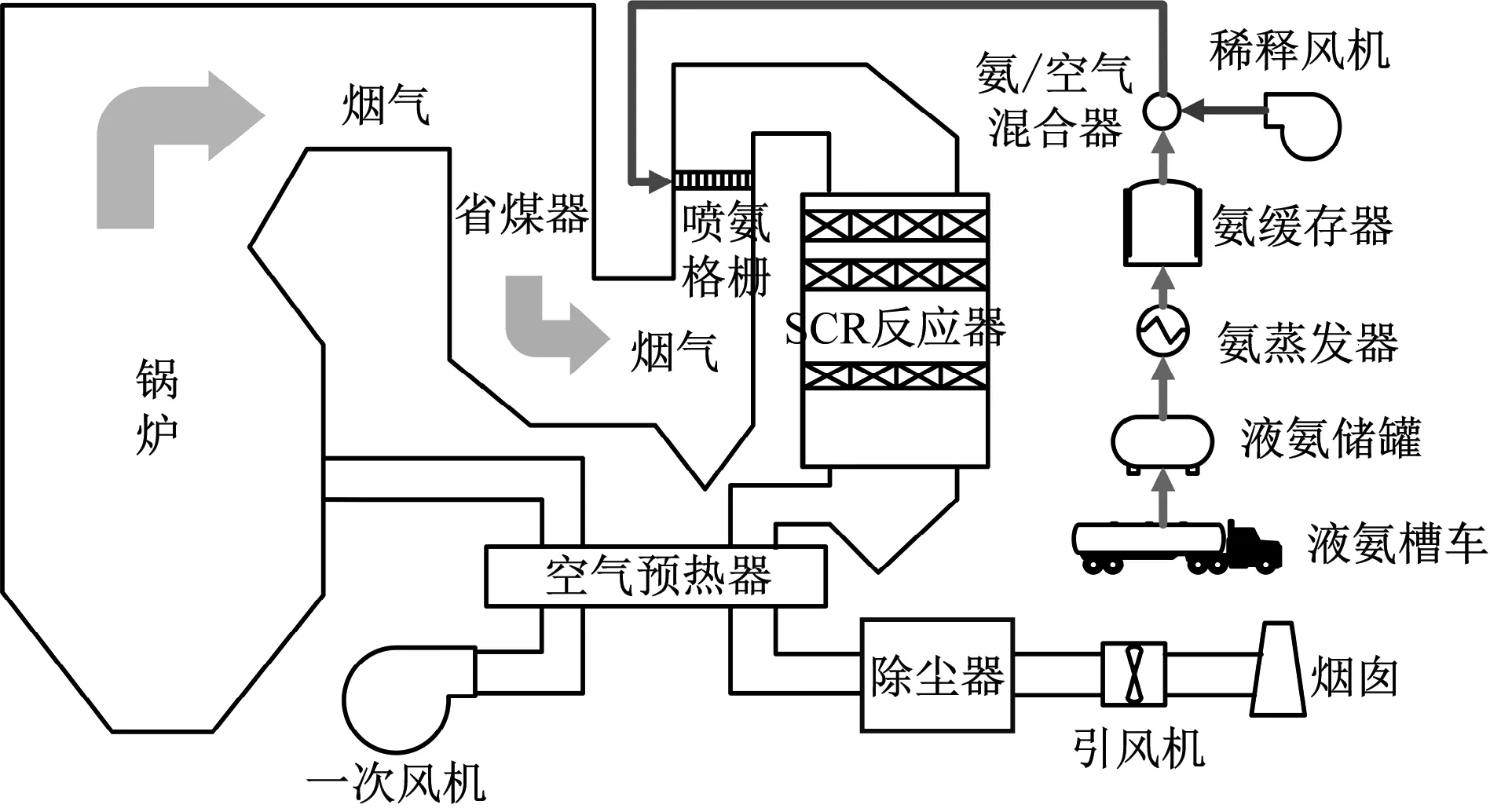
图1 SCR脱硝系统
喷氨量过低,SCR脱硝系统出口NOx质量浓度会增加,不仅无法满足排放最低标准指标,还会污染环境。喷氨量过高可以减少出口NOx质量浓度,但会造成氨逃逸,堵塞SCR下游设备。喷氨量一般由喷氨阀门控制,喷氨量控制过程的平稳对喷氨阀门的寿命有很大影响,因此喷氨量以及喷氨阀门的控制是SCR脱硝系统中至关重要的环节。
1.2 复合串级控制系统
在SCR脱硝系统中,如果只采用简单的直接控制会使氨气阀门长期震荡,影响阀门寿命,因此火电机组现场常常采用串级控制。强化学习复合串级控制系统如图2所示,Gv(s)为阀门开度到喷氨量的内回路模型;Gp(s)为喷氨量到出口NOx质量浓度的外回路实际模型;din(s)为作用于喷氨量的内部扰动;dout(s)为作用于出口NOx的外部扰动;Gd(s)为外部扰动通道;r为出口NOx质量浓度设定值;y为出口NOx质量浓度测量值;u(s)为喷氨量;c(s)为DOB修正前的喷氨量。在脱硝过程中,喷氨量到出口NOx质量浓度这一阶段会受到大量扰动,为了更好地抑制此过程的干扰,引入DOB估计扰动并进行前馈补偿。DOB位于图中虚线框内,其中gn(s)为外回路名义模型Gn(s)的最小相位部分,e-θns为外回路名义模型的纯滞后部分,其中θn表示滞后时间;Q(s)为低通滤波器[10]。从图2可以看出,系统的总扰动为:
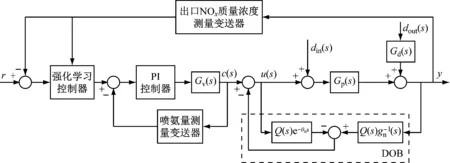
图2 SCR脱硝系统复合串级控制
Dtol(s)=Din(s)+Dout(s)+Dm(s)=
Gn(s)din(s)+Gd(s)dout(s)+[Gp(s)-
gn(s)e-θns][u(s)+din(s)]
(1)
式中:Dtol(s)为系统总扰动;Din(s)为内部扰动;Dout(s)为外部扰动;Dm(s)为模型不匹配造成的扰动。
因此系统输出为:
y=gn(s)e-θnsu(s)+Dtol(s)
(2)
(3)
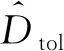
(4)
假设系统稳定时总干扰的时域原函数dtol(t)有界,根据定义可知:
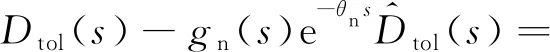
Dtol(s)-Q(s)e-θnsDtol(s)=
[1-Q(s)e-θns]Dtol(s)
(5)
根据终值定理可得:
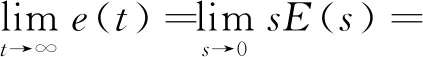
(6)
当选择Q(s)为低通滤波器时,由于其稳态增益为1,因此有e(∞)=0,说明DOB可以有效地抵消干扰[10]。
2 强化学习基础
2.1 强化学习原理
在机器学习的分类中,强化学习与监督学习和非监督学习之间有着明显的差异,其完全不需要事先准备任何数据,而是通过智能体与环境之间进行交互产生动作、状态以及对动作的奖励,通过收集这些与控制相关的数据学习得到最优的控制策略,并不断对模型参数进行更新[11]。
几乎所有的强化学习算法都是基于马尔可夫决策过程构建的[12],一般情况下可以用一个五元组(S,A,R,p,γ)来描述,五元组分别为环境状态的集合、策略产生动作的集合、执行动作后奖励的集合、状态的转移概率和折扣系数[13]。智能体(agent)通过计算累积奖励期望的最大值来获得最佳的控制策略μ*。策略μ产生动作后在状态s下的奖励期望如下:
Qμ(s,a)=Eμ[Rt|s,a]
(7)
式中:Qμ为动作价值函数;s为当前状态;a为状态s下采取的动作;Rt为累计奖励。
将式(7)转化为Bellman公式来计算未来的累计奖励期望,具体公式如下:
Qμ(s,a)=Eμ[Rt+γQμ(s′,a′)|s,a]
(8)
式中:s′为下一时刻的状态;a′为下一时刻的动作。
当采用无模型强化学习算法时,不需要计算状态转移概率,而是通过迭代Bellman公式获得近似的最优策略[11]。
(9)
以上函数求解方法虽然简单,但无法控制复杂的连续系统,因此需要采用神经网络拟合复杂的函数,并采用梯度下降的方法求解以获得最优策略。
2.2 深度确定性策略梯度算法描述
谷歌团队借鉴深度Q学习算法提出了可以用于连续动作控制的深度确定性策略梯度(DDPG)算法,因此笔者以DDPG算法为基础对SCR脱硝系统的控制进行研究。
DDPG算法在与SCR脱硝系统进行交互后会产生动作、状态和奖励值,将这些经验数据储存于经验池中,当DDPG算法进行策略学习时,随机从经验池采样数量为M的(st,at,rt,st+1)样本,其中st、at和rt表示t时刻的环境状态、策略产生的动作以及奖励,st+1表示t+1时刻新的环境状态。DDPG算法的深度学习部分由Actor网络和Critic网络组成,该算法将策略梯度和随机梯度相结合,因此Actor网络和Critic网络均由2套神经网络——target网络和online网络组成。target网络采用软更新,online网络采用梯度更新。这种双网络机制减少了数据的相关性,有利于网络的进一步收敛。Actor网络和Critic网络分别用来产生动作决策以及对动作决策进行评价,对动作决策的评价指导着动作决策的更新方向。各网络的更新方式如下。
Q(s,a|θQ)为Critic online网络的输出Q值。Actor online网络对策略参数θμ进行更新,并根据输入的矩阵状态s选择使输出Q值最大化的动作输出a,a=μ(s|θμ)+N,其中N为随机噪声。在与环境交互后会产生下一时刻的状态和奖励。Actor网络的更新公式[14]如下:
∇θμJ(θμ)≈
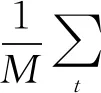
(10)
式中:∇θμJ(θμ)为性能指标对Actor online网络参数θμ的梯度;∇aQ(s,a|θQ)为输出Q值对动作a的梯度;μ(s|θμ)为Actor online网络学习到的策略;∇θμ(s|θμ)为μ(s|θμ)对参数θμ的梯度;上标μ表示Actor online网络。
Critic online网络根据输入的状态s和动作a计算输出Q值,具体更新公式[15]如下:
(11)
yt=r(st,at)+γQ′[st+1,μ′(st+1|θμ′)|θQ′]
(12)
式中:L为Critic online网络的损失函数,通过最小化L来更新网络参数;yt-Q(st,at|θQ)为时序差分(TD)误差,其中yt为TD目标值;上标Q′表示Critic target网络,μ′表示Actor target网络。
target网络根据online网络的赋值对参数进行软更新。公式如下:
θQ′←τθQ+(1-τ)θQ′
(13)
θμ′←τθμ+(1-τ)θμ′
(14)
其中,τ为软更新系数,τ越小,网络更新的幅度越慢,算法越稳定,但学习速率也越慢。
3 强化学习控制器设计
3.1 TD3算法
DDPG算法虽然在连续任务中有优势,但其在获得错误动作后很容易朝着错误的方向进行,在有限时间内会造成低效率学习,DDPG算法还存在Q值过高、探索能力较差和控制不稳定等问题,针对这些缺点,Fujimoto等[16]对DDPG算法进行改进,提出了双延迟深度确定性策略梯度(TD3)算法。TD3算法相比DDPG算法主要改进了以下3点:
(1) 双Critic网络[17]。在DDPG算法的基础上增加了一套完全独立的Critic网络,使用min函数比较2套Critic target网络的Q′,选取最小Q′值并将此值作为更新目标进行更新,用来解决Q值估计过高的问题。改进后的公式如下:
(15)
(2) Actor网络延迟更新[18]。Critic网络估计误差较大时,Actor会朝着错误的方向产生新动作,错误次数的增加会大大降低训练效率,严重时会产生局部最优,因此Actor网络需要在Critic网络进行多次更新后再进行更新,降低Critic错误更新造成的危害,提高Actor网络的收敛速度。
(3) 目标策略平滑[19]。在Actor target网络中添加随机噪声,防止Q值出现过拟合,增加算法稳定性。具体公式如下:
(16)
3.2 ITD3算法
SCR脱硝控制系统已知的环境状态有出口NOx质量浓度测量值以及设定值与测量值之间的误差,TD3算法单单依靠这2个环境状态变量很难获得较好的控制策略。PID是实际工业过程控制中使用最普遍的控制器,因此借鉴PID控制思想提出了一种ITD3算法,算法原理如图3所示。ITD3算法在收集状态信息后计算出口NOx质量浓度设定值与测量值之间误差的微分和积分,将误差的微分和积分作为SCR脱硝系统新生成的环境状态,与出口NOx质量浓度测量值、误差同时储存于经验池中,大大增加了策略学习的数据量。通过与PID控制思想的结合,使ITD3算法可以更好地应用于工业过程控制。
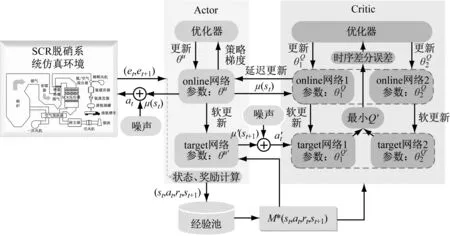
图3 ITD3算法原理图
3.3 奖励机制设计
强化学习的奖励机制是实现有效控制的关键,离散的奖励机制有助于控制系统快速远离较差的策略,但离散奖励过多会增加算法的复杂性。而连续的奖励机制可以加快算法收敛,使控制过程更加流畅平滑[20],因此将离散奖励机制与连续奖励机制相结合,具体奖励公式如下:

(17)
式中:e为出口NOx质量浓度设定值与测量值之间的误差;λ为为了防止奖励值过高而造成策略过度更新的系数,取0.1。
3.4 Actor网络和Critic网络设计
在ITD3算法中,Actor网络和Critic网络均使用全连接神经网络来表示,神经网络的结构图见图4。Actor online网络和Actor target网络输入为收集到的环境状态,输出为作用于环境的动作。Actor网络共有2个隐含层,神经元个数分别为50和20,2个隐含层激活函数分别为softplus和tanh,softplus相当于relu平滑后的函数,其导数一直存在,可以有效防止relu函数出现神经元死亡的问题。Critic online网络和Critic target网络输入为环境的状态和决策产生的动作,状态路径有3个隐含层。第一个隐含层包括100个神经元,选取softplus作为激活函数,第二个隐含层包括50个神经元,选取relu作为激活函数,第三个隐含层包括25个神经元。动作路径有2个隐含层,神经元个数分别为50 和25,第一个隐含层的激活函数选用softplus。之后将状态路径和动作路径的最后一层通过add层进行合并,add层的激活函数采用relu,最后输出Q值。

图4 神经网络结构图
4 仿真结果与分析
4.1 实验准备
将线下训练好的ITD3控制器作为主控制器对外回路进行实时控制。为了防止阀门调节过大采用PI控制器控制内回路。PI控制器的参数设置为:比例系数Kp=4.25,积分时间常数Ti=2.24。内回路选取540 MW下阀门开度到喷氨量的传递函数:
(18)
外回路选取540 MW下喷氨量到出口NOx质量浓度的传递函数[21]:
(19)
根据SCR脱硝系统的模型阶次选取合适的低通滤波器:
(20)
ITD3控制器在线下训练时每次迭代随机生成出口NOx质量浓度的设定值和初始值,通过在随机空间内进行不同控制目标的试错来完成与环境的交互以及策略的学习,随机生成的设定值和初始值的范围均为(20,60)mg/m3。ITD3算法与TD3算法参数设置相同,具体如下:最大迭代次数为1 200,折扣系数γ=0.99,采样时间Ts=1 s,仿真时间Tf=150 s,Critic学习率为10-3,Actor学习率为10-4,梯度下降使用的优化器为adam,加载预训练模型=true;神经网络L2正则化系数均为10-4;误差积分的下边界设置为0,其余状态边界均设置为∞;批次样本数量为128,软更新系数τ=10-3,经验池大小为106次,策略延迟更新频率为4,策略噪声方差为1.2,策略噪声方差衰减率为10-5,动作噪声方差为0.8,动作噪声方差衰减率为10-5。
4.2 工况对比
为验证控制性能,对ITD3-PI复合串级控制与TD3-PI复合串级控制、复合串级PID控制和串级PID控制进行对比实验,其中复合串级PID控制除主控制器与ITD3-PI复合串级控制不同外,其余均相同。
工况一,在450 s时将控制器输入端(图2)的出口NOx质量浓度设定值从50 mg/m3调整为30 mg/m3,仿真结果见图5。从图5可以看出,由于没有加入任何扰动,复合串级PID控制和串级PID控制性能完全相同。未改进的TD3-PI复合串级控制只能将出口NOx质量浓度测量值以及设定值与测量值之间的误差这2项数据作为环境状态进行策略学习,由于策略学习数据不足导致无法对大迟延、大惯性的SCR脱硝系统进行有效控制。ITD3-PI复合串级控制到达设定值50 mg/m3的上升时间和峰值时间最快,调节时间与复合串级PID控制相当,超调量要小于复合串级PID控制,控制动作更加平滑;ITD3-PI控制在设定值改变后的上升时间与其他控制算法相差不大,峰值时间、调节时间和超调量小于其他控制算法,控制动作整体要比其他控制算法更平稳。综上所述,在设定值改变前后ITD3-PI复合串级控制器均可以达到更加快速稳定的控制效果。

图5 工况一控制策略对比曲线
工况二,在控制器的设定值输入端加入连续的噪声干扰,噪声服从标准正态分布,频率为0.1 Hz。仿真结果见图6,由于TD3-PI复合串级控制效果太差将不再进行对比实验。由图6可知,ITD3-PI复合串级控制算法在噪声存在的情况下基本没有波动,由于扰动加在控制器之前,复合串级PID控制和串级PID控制性能完全相同,会受设定值输入信号噪声的影响而波动,表明ITD3-PI复合串级控制器在应对控制器输入信号的噪声干扰时控制性能更好。
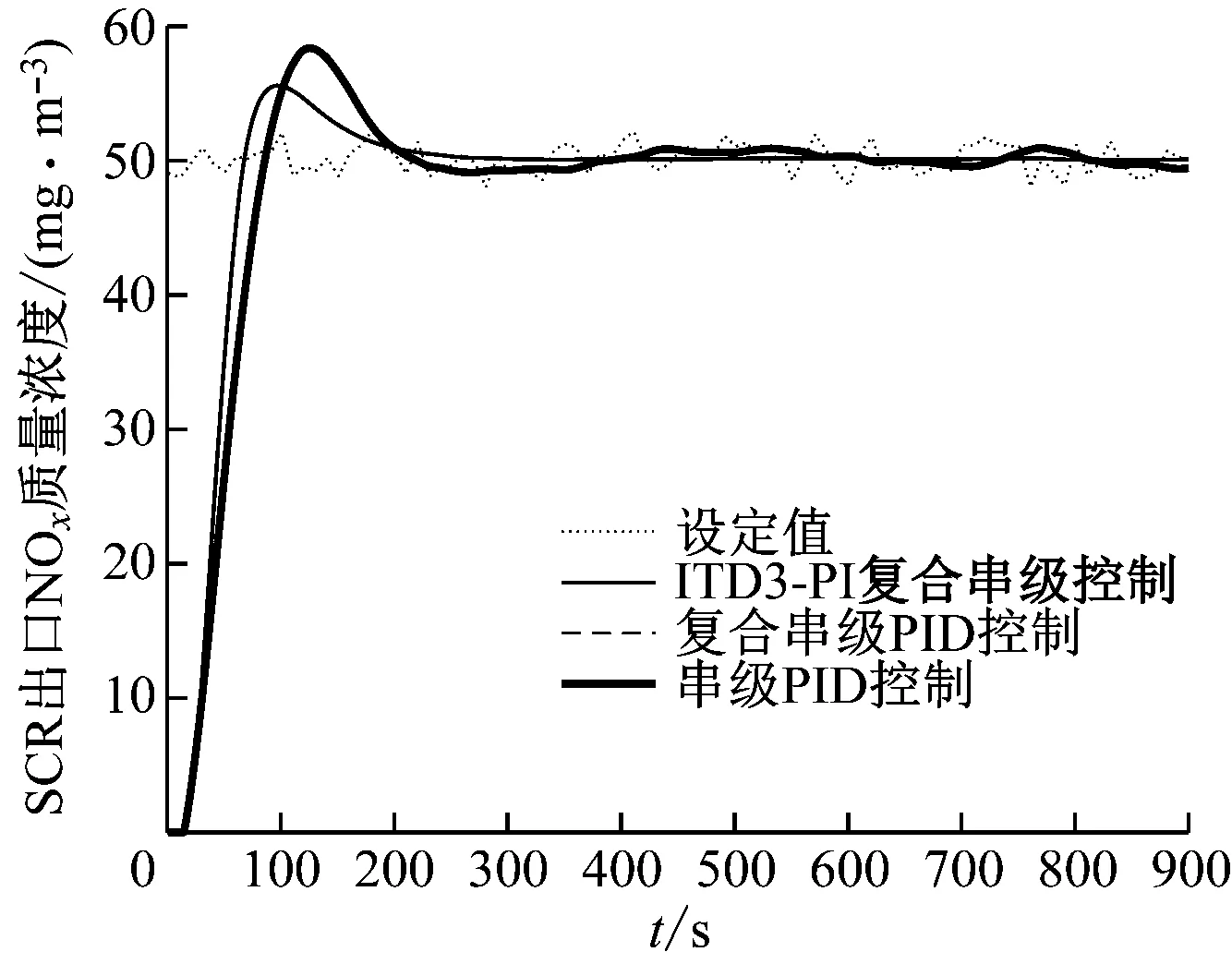
图6 工况二控制策略对比曲线
工况三,450 s时在喷氨到NOx模型输入端之间加10%阶跃扰动,仿真结果如图7所示。从图7可以看出,在加入阶跃扰动后ITD3-PI复合串级控制算法的调节时间小于其他2种控制算法,超调量小于复合串级PID控制,比串级PID控制小很多,ITD3-PI复合串级控制算法在加入内部扰动后可以快速稳定地恢复到之前位置,抗干扰性能更好。

图7 工况三控制策略对比曲线
工况四,450 s时在NOx模型输出端之后加入10%的阶跃扰动,取扰动通道模型为:
(21)
仿真结果如图8所示。从图8可以看出,在加入阶跃扰动后ITD3-PI复合串级控制算法的调节时间小于其他控制算法,超调量略小于其他控制算法,可以快速稳定地恢复到之前位置。表明DOB在扰动抑制方面起到较好的作用,ITD3-PI复合串级控制算法在加入外部扰动后抗干扰性能更好。
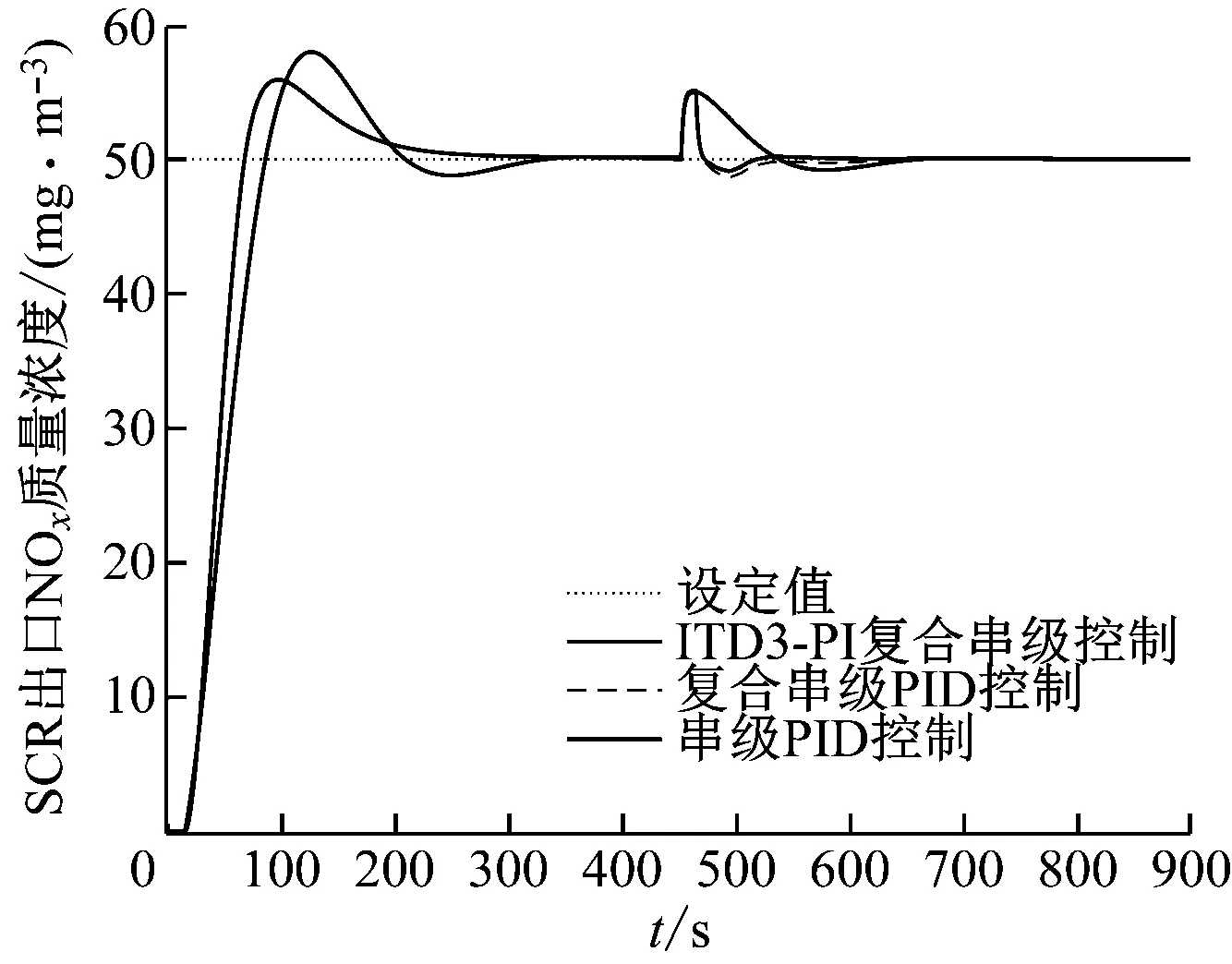
图8 工况四控制策略对比曲线
为了进一步验证ITD3-PI复合串级控制算法的控制性能,计算4种工况下各控制算法的绝对误差积分(IAE),结果见表1。由表1可知,本文所提方法在4种工况下的IAE值均小于其他控制算法,证明了本文方法具有更好的综合控制性能。

表1 各工况下的IAE值
5 结 论
针对SCR脱硝系统的特点,提出了一种ITD3-PI复合串级控制算法。首先,借鉴PID控制思想提出了一种ITD3算法,通过对出口NOx质量浓度设定值与测量值之间的误差进行微分和积分运算生成新的环境状态,并将新的状态与测量值、误差同时储存于经验池中,经过改进大大增加了策略学习所需的数据量,使ITD3算法可以更好地用于工业过程控制;然后,利用DOB来估计脱硝过程的扰动,并进行前馈补偿;最后,对所提方法进行仿真对比实验,仿真结果表明本文所提方法控制速度快、超调量小、抗干扰能力强,该控制方案可以为强化学习在SCR脱硝系统中的应用提供新的思路。

