基于OSSK调制的MIMO星地激光通信上行链路系统

王千千,王海波,王 怡

(中国计量大学 信息工程学院 浙江省电磁波信息技术与计量检测重点实验室,浙江 杭州 310018)

星地激光通信利用激光代替微波作为通信载体在卫星与地面光学站之间传递信息,具有无频谱限制、带宽宽等特点[1]。然而激光光束穿越大气时,近地面湍流引起的折射率起伏将影响光束的传输质量,破坏激光光束的相干性,从而引起光强闪烁、光束漂移和到达角起伏等一系列大气湍流效应[2-4]。光束漂移是由于受到大于光束直径的涡旋影响,导致光束传播方向发生随机偏折,下行链路中传输光束到达近地面湍流时,其直径已远大于大气的涡旋尺度,所以下行链路的光束漂移很小,因此本文主要分析星地激光通信上行链路的情况。

可以利用调制技术和多输入多输出(MIMO)技术提高星地激光通信系统的可靠性。2013年李密将最小位移键控(MSK)引入星地激光通信中,分析了基于对数正态分布MSK方案在上行链路中的系统性能[5]。2020年Nancy Alshaer分析了采用M-ary相移键控(MPSK)调制的单输出多输入(SIMO)星地激光通信系统在大气湍流下的性能,利用Gamma分布表征光强闪烁、光束漂移的联合影响[6]。2020年李康宁研究了在Gamma-Gamma分布下,基于差分相移键控(DPSK)调制的MIMO星地激光通信系统[7]。MSK、MPSK、DPSK等传统调制,都是从复杂调制字母表中选择符号来传递信息位元,信道引入的复杂衰落将导致传输符号幅度和相位失真。有一种考虑复杂信道衰落系数本身构成调制字母表的方法,即空间移位键控(SSK)调制。2009年Jeyadeepan Jeganathan在无线射频领域提出并分析了SSK调制,与空间调制相比具有更低的计算开销和硬件要求[8]。将其引入激光通信中我们称之为光学空间移位键控(OSSK)调制[9-10]。

OSSK是用于星地激光通信的一种有前景的调制方式,它的频率和带宽效率都很高。在OSSK中,任意给定时间多个发射单元只有一个发射器处于活动状态,OSSK在选定天线上传输信息。在不影响系统性能的前提下,避免了信道间干扰(ICI),减轻了发射机对天线间同步的需求,从而避免了传统MIMO技术伴随的复杂性和成本缺陷[11-12]。据我们所知,在星地激光通信中OSSK调制还未见报道。

基于上述的分析,本文提出了OSSK调制的MIMO星地激光通信上行链路系统,利用Málaga(M)分布表征近地面湍流光强闪烁、光束漂移、到达角起伏的联合影响。推导了OSSK调制的星地激光通信上行链路误码率的闭合表达式。仿真分析了信噪比和天顶角对系统误码率的影响,并且与DPSK、MSK等传统调制进行了对比,最后通过蒙特卡洛对推导数据进行了验证。

1 系统与信道模型

1.1 OSSK调制系统模型

考虑一个如图1所示的OSSK系统,其中Nt和Nr分别为信号传送器(Txs)和信号接收器(Rxs)的数量。传入的信息位在SSK编码器上被分割成位的组合。基于m位,SSK编码器激活其中一个激光器,并关闭所有其他激光器。这样,每单位时间间隔传输m比特,因此OSSK具有的频谱效率,并且随着Txs数目的增加而提高。SSK编码器是一个将传输链(放大脉冲)连接到一个激光模块的开关。由有源激光器发出的光脉冲受到大气湍流的影响,通过大气通道到达光探测器。从数学上讲,输入输出关系可以表述为

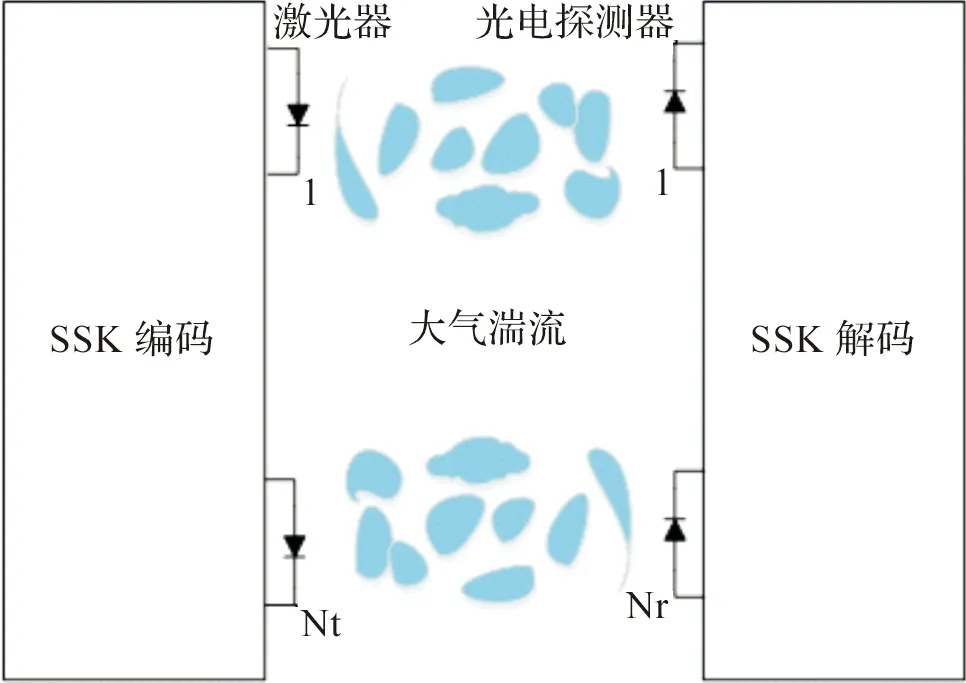
图1 OSSK调制系统模型Figure 1 OSSK modulation system model

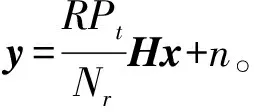
(1)

上式中,y=RNr×1是接收向量,x∈R1×Nt是发射向量,Pt是发射功率,R表示光电探测器的探测效率。n表示均值为零,方差为σ的加性高斯白噪声。H∈RNr×Nt表示通道增益矩阵,其表达式如下：

(2)

式(2)中,hij表示的是第j个激光器和第i个光电探测器之间的信道增益,j=1,2,…,Nt,I=1,2,…,Nr。探测器在考虑的系统中的主要功能是确定光学Tx指数。在这种情况下,最优检测器是最大似然检测器

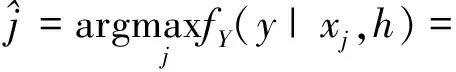
(3)

1.2 信道模型

在星地激光通信上行链路中,M分布可以表征现在大多数大气模型,例如K分布、Gamma-Gamma分布等,而且M分布涵盖弱、中、强湍流的所有通道条件。考虑光强闪烁、光束漂移、到达角起伏的综合影响,故M分布信道模型的概率密度表达式[13]:

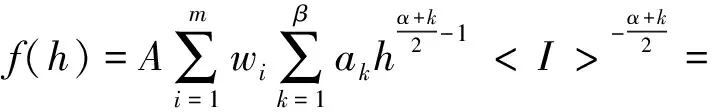
(4)

其中:

(5)

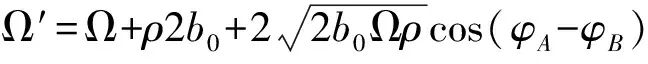
2 性能分析

在OSSK调制的MIMO星地激光通信上行链路系统中误码率的上界为[14]

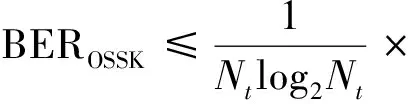
(6)

dH(dk,dj)表示符号dk和dj之间的汉明距离,P(k→j|H)为符号dk和dj的成对错误概率,表示为

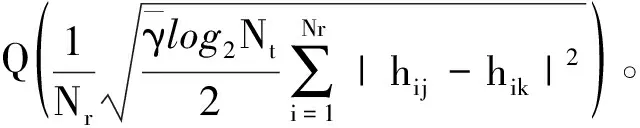
(7)

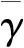
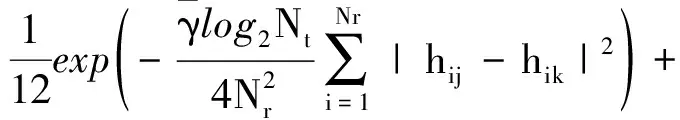
(8)

我们令Uijk=hij-hik,可以得到Uijk的PDF为[15]

fUijk(Uijk)=

(9)

经过t=ln(hik)的简单变换,再利用Hermite多项式将公式(9)转化为[16]

fUijk(Uijk)=

(10)

式(10)中xi和wl分别代表了Hermite多项式的根和权重,并且1≤l≤N。

令γijk=|Uijk|2-γ,可以得到的概率密度表达式为

fγijk(γijk)=

(11)

将公式(11)转化成对应的矩母函数(MGF),公式为[17]

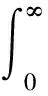
(12)

Mγijk(-s)独立于ijk,因此Mγijk(-s)=Mγ(-s)∀ijk。

利用广义高斯拉盖尔公式将公式(12)转化为[18]

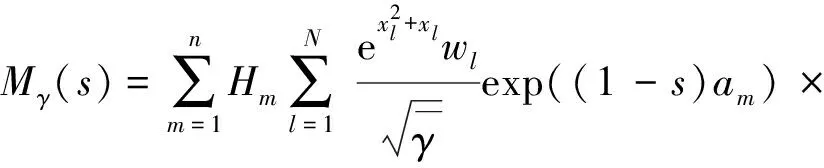
(13)

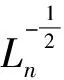
(14)

MIMO星地激光通信上行链路OSSK调制系统的平均误码率上界为

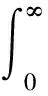
(15)

3 仿真结果和分析

图2显示在大气湍流条件下信噪比与误码率的关系,可以看出推导数据与蒙特卡洛仿真十分贴近,验证了推导的正确性。五种方案的误码率都随着信噪比的增大而减小。当Nt=1,Nr=1,DPSK调制、MSK调制的误码率始终大于OSSK调制方案的误码率,为满足通信误码率的最低要求10-5,DPSK、MSK、OSSK调制方案所需的信噪比分别为75 dB、72 dB、48 dB。在达到相同误码率情况下,OSSK调制是一种有效的减少发射功率、降低系统消耗的方法,进而降低星上终端激光温控的难度。对比三种OSSK调制方案,可以发现增加发射天线对系统误码率的改善并不明显,增加接收天线,可以显著降低误码率,当信噪比为30 dB时,Nt=1,Nr=2 OSSK方案的误码率比Nt=1,Nr=1 OSSK方案低约4个数量级,并且随着信噪比的增大,这种优化更加显著。因此,增加OSSK调制的接收天线数量可以进一步提高系统性能,OSSK调制在星地激光通信领域具有广阔的应用前景。

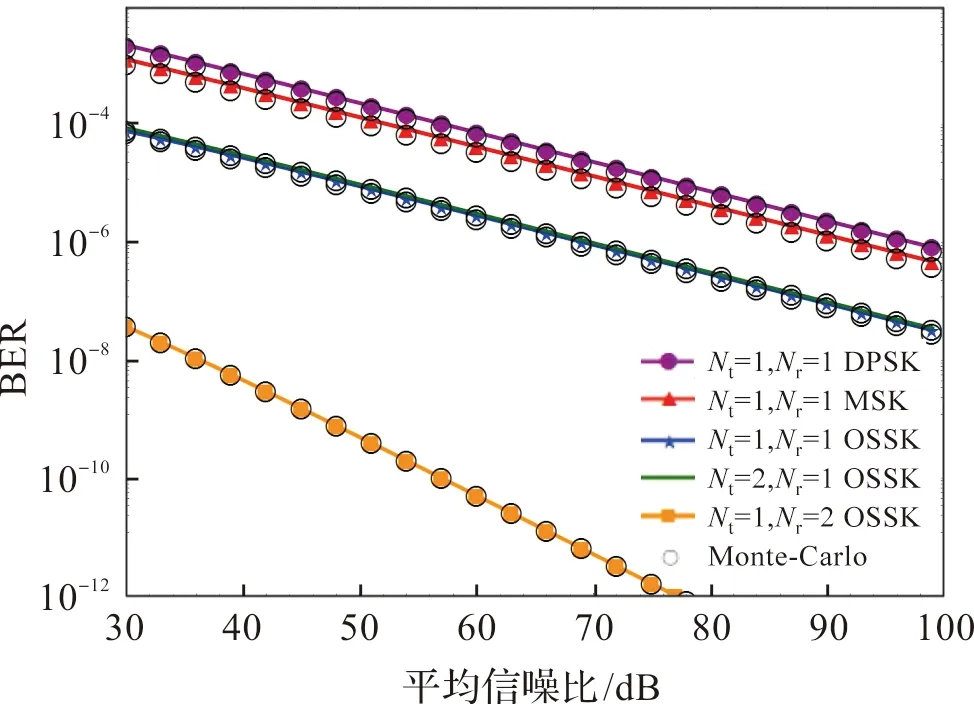
图2 DPSK调制、MSK调制与OSSK调制信噪比与误码率的关系Figure 2 Relationship between signal-to-noise ratio and bit error rate of DPSK modulation, MSK modulation and OSSK modulation

图3给出了天顶角与误码率之间的关系,信噪比取60 dB,天顶角是星地激光通信中特有的可以改变大气湍流参数的物理量。DPSK调制、MSK调制和OSSK调制系统的误码率都随着天顶角的增大而单调递增,这说明高天顶角对系统性能的影响更为严重。以天顶角40°,Nt=1,Nr=1为例,DPSK调制、MSK调制和OSSK调制的系统误码率为3.2×10-5、1.8×10-5、9.0×10-7,OSSK方案系统性能始终优于两种传统调制方案。为使系统误码率达到10-5,从趋势上看,Nt=1,Nr=2 OSSK调制方案的最大天顶角最大。在实际工程应用中,OSSK调制方案可以通过增加接收天线来获得更大的最大天顶角。较大的天顶角可以扩大单颗卫星的覆盖面积,进而降低星地激光通信的成本。

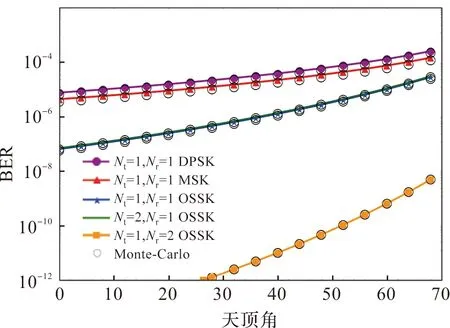
图3 DPSK调制、MSK调制与OSSK调制天顶角与误码率的关系Figure 3 Relationship between zenith angle and bit error rate of DPSK modulation, MSK modulation and OSSK modulation

束散角同时影响着光束漂移和接受光强的的强度,只有选取适当的束散角,才能获得最优的误码率性能。图4给出了束散角与误码率之间的关系,信噪比取60 dB,五种方案的误码率都存在一个最低点,误码率最低点对应的束散角度为最佳束散角,在最佳束散角条件下,Nt=1,Nr=2 OSSK调制方案系统性能最优,同收发条件下,OSSK调制方案性能也优于其他两种调制方案。

图4 DPSK调制、MSK调制与OSSK调制束散角与误码率的关系Figure 4 Relationship between divergence angle and bit error rate of DPSK modulation, MSK modulation and OSSK modulation

4 结 论

本文提出了OSSK调制的MIMO星地激光通信上行链路系统,给出了光强闪烁、光束漂移、到达角起伏三者综合影响下OSSK调制误码率的闭合表达式。根据仿真结果,我们可以看到在收发天线数目相同的条件下,OSSK调制相较于DPSK调制和MSK调制,系统性能有很大提升,而且OSSK调制达到相同BER要求所需的信噪比小于DPSK调制、MSK调制。增加接收天线的OSSK调制方案系统性能有明显提升。满足相同误码率,单输出单输入的DPSK、MSK、OSSK调制方案所能达到的最大天顶角依次增大,OSSK调制方案可以扩大单颗卫星的覆盖面积。因此OSSK调制可以降低星地激光通信的发射功率,节约系统消耗,降低激光温控的难度,增加接收天线数量可以进一步优化通信系统,降低星地激光通信成本。该研究为MIMO星地激光通信上行链路系统的工程应用提供了理论参考。