星间链路体制下的星地双向时间同步方法

吕宏春，卢晓春，武建锋

(1. 中国科学院国家授时中心，西安 710600；2. 中国科学院大学，北京 100049；3. 中国科学院精密导航定位与定时技术重点实验室，西安 710600；4. 中国科学院大学天文与空间学院，北京 101408；5. 中国科学院大学电子电气与通信工程学院，北京 101408)



星间链路体制下的星地双向时间同步方法

吕宏春1,2,3，卢晓春1,3,4，武建锋1,3,5

(1. 中国科学院国家授时中心，西安 710600；2. 中国科学院大学，北京 100049；3. 中国科学院精密导航定位与定时技术重点实验室，西安 710600；4. 中国科学院大学天文与空间学院，北京 101408；5. 中国科学院大学电子电气与通信工程学院，北京 101408)

推导了星地双向时间同步的数学模型，提出了在星间链路体制下进行星地双向时间同步的方法，计算了新一代导航试验卫星与西安站的相对钟差，通过对计算结果分别按1周、1天和1小时时长进行参数拟合，以及进行短期频率稳定度分析，验证了试验阶段星间链路体制下星地双向时间同步的精度和性能。结果表明，1周、1天和1小时的拟合时长星间链路体制下的星地时间同步精度分别达到了3.42纳秒、0.30纳秒和0.15纳秒，10000秒频率稳定度优于8×10-14。

星间链路; 星地时间同步; 时分体制; 北斗卫星导航系统

0 引 言

建立星间链路(Inter-satellite link，ISL)，实现自主导航，主要目的就是支持GNSS持续进行高精度卫星星历和钟差估计，即定轨和时间同步，使导航系统在失去地面支持情况下具有一定的自主运行能力，同时解决我国北斗导航系统难以全球布站的问题[1]。我国从2015 年3月30号发射的新一代北斗导航卫星上开始增加了Ka频段星间链路设备，开展星间链路工作。通过星间链路测量和时间同步可以得到卫星间的相对钟差，将星地双向时间同步技术应用于星间链路对地测量中可在星间链路体制下获得星地钟差。我国采用一种时分的星间链路体制，上下行链路同频，在星地双向时间同步中能消除电离层时延影响，有望获得更高的星地时间同步精度。针对星间测量及时间同步需求，文献[2]提出了一种动态环境下基于伪码高精度距离测量和时间同步的技术，并通过仿真得到了厘米级的测距精度和优于1 ns的时间同步精度；文献[3]以卫星双向时间同步算法为基础，针对卫星相对运行造成星间距离变化特点，提出了一种卫星动态双向时间同步算法，仿真得到了优于5 ns的精度；文献[4]针对相对论效应对星间测量的影响，提出了带有相对论效应修正的双向单程测距与时间同步算法。

传统的星地双向时间同步技术已成功应用于北斗区域卫星导航系统(北斗二号)卫星钟差的测量，国内对星地双向时间同步方法已有较多研究，文献[5]建立了用于星地双向时间同步的模型，并通过试验数据获得平均约0.34 ns的拟合精度；文献[6]将星地双向时间同步技术应用于北斗卫星试验阶段，得到1 ns单弧段拟合精度；文献[7]在星地测量中考虑卫星运动因素，提出了一种基于最小二乘拟合的星地动态双向时间同步和测距算法，可有效消除卫星运动对双向时间同步和测距的不利影响。

传统的星地双向时间同步技术不能直接应用于星间链路的对地链路，本文针对星间链路时分体制下星地链路的特点，对时分观测的双向单程伪距进行历元归算，推导星地双向时间同步数学模型，对星间链路体制下的星地双向时间同步方法进行研究，验证了试验阶段星间链路体制下星地双向时间同步的精度。

1 星间链路体制下的星地双向时间同步原理和数学模型

1.1 传统星地双向时间同步方法

传统的星地双向时间同步中卫星和地面站在相等的钟面时互发信号[8]，双向单程伪距为：

(1)

(2)

(3)

(4)

对系统时的计算需要卫星、地面钟差模型支持，此处可以使用预报钟差模型代替，也可暂以钟面时代替，待求解出钟差模型后再代入式(4)重新计算。

伪距观测量以本地时钟的信号接收时刻记录，则信号发射时刻为：

(5)

钟差是时变的，由于光行时影响，在信号传播过程首末的钟差有所差异。GEO和IGSO卫星轨道高度35786km，MEO卫星轨道高度21528km，则GEO和IGSO星地测距中的光行时约为0.12s，MEO星地测距中的光行时约为0.07s。统计2015年11月全部在轨GPS卫星和北斗卫星的钟速，结果表明除北斗C05和C14外其余卫星钟速绝对值均小于5×10-11。则以GEO卫星为例，由光行时引起的信号传播过程首末卫星钟差差值小于0.006ns，对于0.1ns量级的时间同步精度而言可以忽略不计；C05钟速绝对值达到约4×10-10，由此带来的卫星钟差差值约0.048ns，对于0.1ns量级的时间同步精度不可忽略。顾及钟速绝对值较大的情况，在星地双向时间同步过程中需要考虑由于光行时引起的信号传播过程首末卫星钟差的变化，同理也应考虑地面站钟差的变化。

传统的星地双向时间同步中卫星和地面站在相等的钟面时互发信号，将星地双向单程测量中卫星钟差、地面钟差分别记作 ΔTs和ΔTr，则

(6)

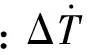
(7)

由于上下行伪距近似相等，则式(7)可改写为：

(8)

由于上下行链路近似对称，卫星星历误差、地面坐标误差及信号传播过程中的对流层时延等公共误差项将削弱或抵消，这是双向时间比对能获得高精度的主要原因。双向时间同步的核心策略即是尽量保证上下行链路的对称性，对造成非对称的诸如电离层时延、Sagnac效应、光行差、通道时延等项进行修正。利用卫星星历分别计算各卫星在相应系统时的坐标，可以修正光行差；对通道时延可提前进行标定并扣除；对Sagnac效应既可针对卫星或地面站坐标进行修正[9]，也可以直接修正其造成的路径方向延迟[10]；在传统的星地双向时间同步中上下行链路不同频，导致上下行电离层时延不同，需使用电离层时延修正模型进行修正。

相对论效应τrel可以利用卫星星历参数或者三维坐标及速度矢量通过公式准确计算，方法如式(9)所示[11-12]：

(9)

也可用式(10)形式：

(10)

式中：R和V分别表示卫星瞬时三维坐标及速度矢量。

星地双向时间同步得到的结果为星地相对钟差值，已知地面钟差可得到卫星钟差。不同频点、不同系统之间可能存在零值偏差，需要对包含设备通道时延在内的零值偏差进行标校。

1.2 星地双向时间同步方法在星间链路体制的应用方式

在星间链路体制中双向单程伪距测量值并不是在相同钟面时互发信号，而是采用一种时分体制，即一个时隙完成卫星发射信号以及地面接收信号的过程，下一个时隙完成地面发射卫星接收的过程。为将星地双向时间同步方法应用于星间链路体制，必须首先对双向伪距观测量的历元进行归算，使双向单程伪距归算到同一观测历元。在传统的星地双向时间同步中，星地双方在同一钟面时互发信号，从而保证了路径的近似对称性，星间链路体制下可以将双向单程伪距观测量归算到同一钟面时互收信号，也保证了路径的近似对称性。对已进行历元归算的星地双向伪距观测量可按照传统的星地双向时间同步方法进行计算。

可使用多项式插值的方法实现历元归算，多项式插值法直接以伪距观测值为插值节点，对历元归算时刻进行插值计算。拉格朗日插值是多项式插值的典型代表，n阶拉格朗日插值函数定义为[13]：

(11)

式中：xk和yk组成插值基节点对，对于伪距插值而言xk为插值节点时刻，yk为插值节点时刻对应的伪距值；x为待插值历元；则对应的函数值fn(x)就是插值结果。拉格朗日插值的阶数n与插值基节点个数m的关系为：m=n+1。

插值精度与观测值的采样间隔及多项式阶数有关，以1分钟间隔的伪距观测值为例，4～6阶拉格朗日插值即可获得优于1mm的插值精度。

在星间链路体制下，星地上下行链路信号频率相同，对于已经进行了历元归算的星地双向伪距观测值，基本可抵消上下行链路的电离层时延。

2 试验分析

在2015年11月15日至2015年11月21日(即北斗515周)使用I1S卫星与西安站进行星间链路体制下的星地双向伪距测量，共得到6d的有效数据(2015年11月21日西安站地面设备未参与试验)。

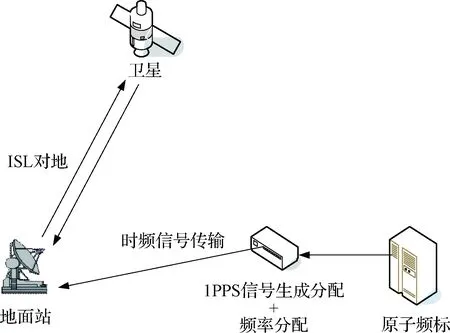
图1 试验系统示意图Fig.1 Sketch map of test system

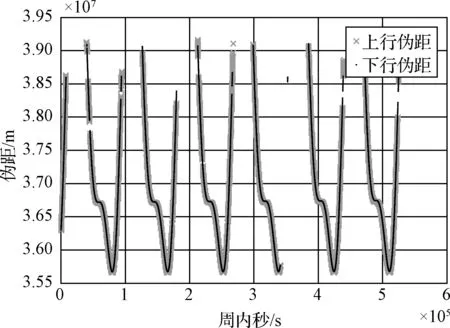
图2 原始观测数据Fig.2 Original pseudorange observations

图1为试验系统示意图，地面站时钟信号由原子频标提供，卫星与地面站通过星间链路体制下的对地测量链路实现星地双向伪距测量。原始伪距观测数据如图2所示。

将星地双向时间同步方法用于星间链路体制中进行钟差计算，利用零值标校手段扣除星间链路设备时延后，与同时段的L波段对该卫星的星地双向时间同步结果进行比较，结果如图3所示。

图3 ISL星地钟差与L波段星地钟差Fig.3 Satellite-ground clock offset of ISL and L band

星地时间同步精度常使用拟合残差来表征，由于拟合残差结果与拟合时长存在较大关联，本文分别计算1周、1天和1小时时长弧段的拟合残差，分析时间同步性能。

对ISL体制下的星地双向时间同步结果按1周弧段时长进行二次三项式拟合，并与同时段L波段双向时间同步的结果的拟合残差对比，拟合残差见图4。

图4 1周时长拟合残差Fig.4 One week time length fitting residuals

对于1周时长的拟合，ISL体制下的星地双向时间同步结果与L波段双向时间同步结果的拟合残差的RMS分别为3.42ns和2.66ns，L波段双向时间同步结果略优于ISL对地比对结果；二者钟速差为-7.4×10-14，以L波段计算结果为参考值，得到ISL体制下的星地双向时间同步结果与L波段计算结果的偏差RMS为1.59ns。结果表明对于1周时长的拟合，ISL体制下的星地双向时间同步结果与L波段结果符合的较好。

计算观测时段较完整的两天的星地双向时间同步结果，并进行1天时长二次三项式拟合，第1天和第2天弧段的结果分别如图5和图6所示。结果表明，对第1天整弧段进行拟合时，ISL体制下的星地双向时间同步结果约在-1.0ns～1.0ns之间波动，拟合残差RMS约为0.5ns；第2天弧段计算结果多在-0.5ns～0.5ns之间波动，拟合残差RMS约0.3ns。

对第1天和第2天的ISL体制下的星地双向时间同步结果每1小时进行一次二项式拟合，得到拟合结果分别如图7和图8所示，ISL体制下弧段1的星地双向时间同步结果拟合残差为0.21ns，弧段2为0.15ns.

图5 第1天弧段1天时长拟合残差Fig.5 One day time length fitting residuals for the 1st day

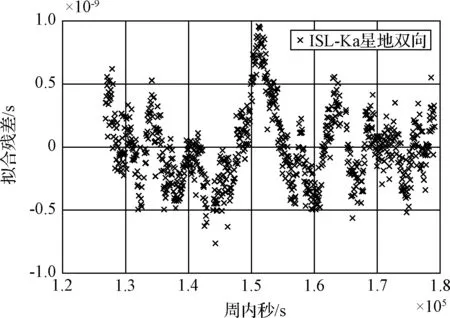
图6 第2天弧段1天时长拟合残差Fig.6 One day time length fitting residuals for the 2nd day

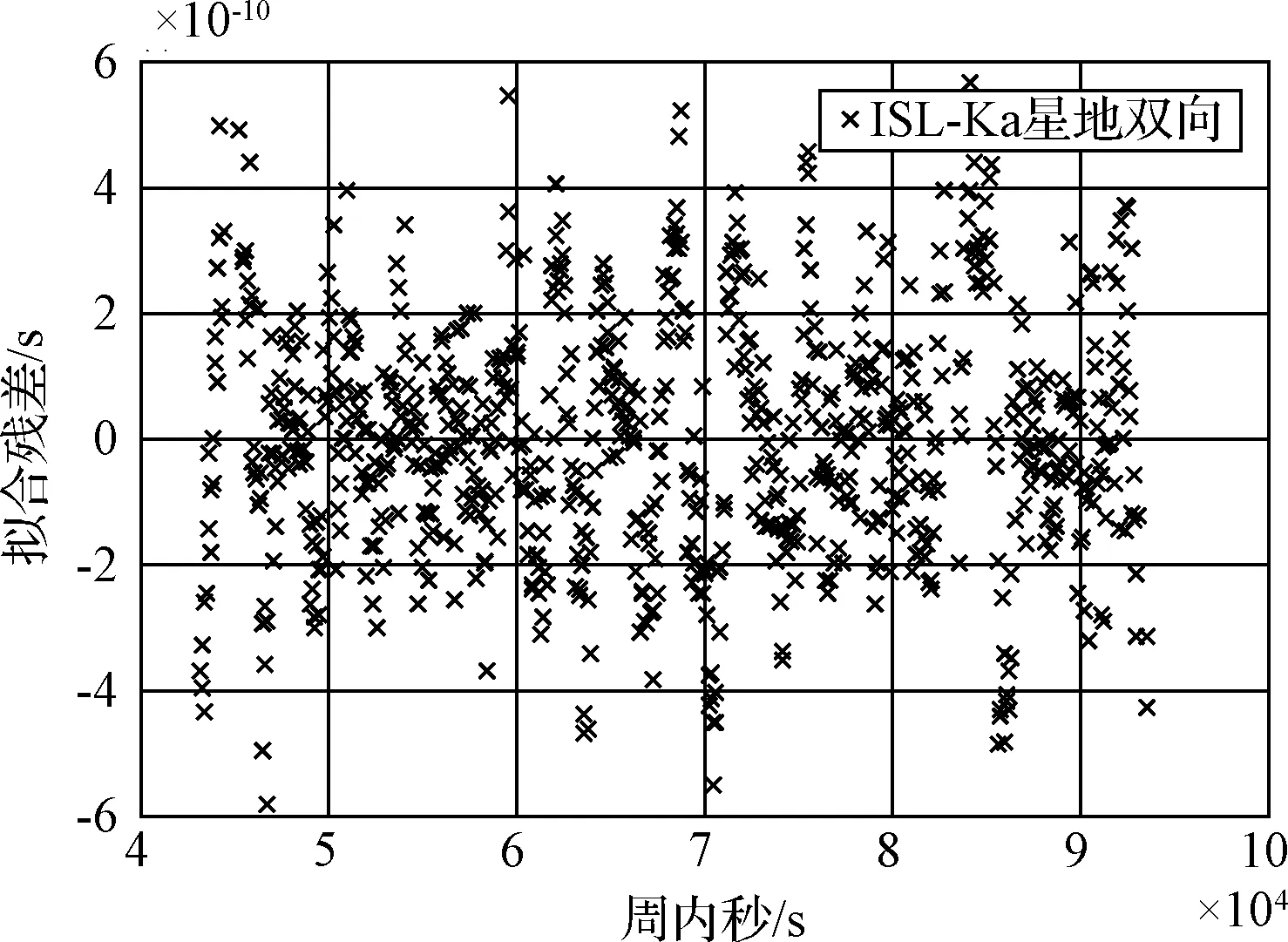
图7 第1天弧段1小时拟合时长拟合残差Fig.7 One hour time length fitting residuals for the 1st day

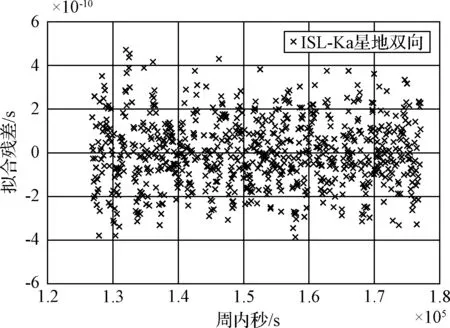
图8 第2天弧段1小时拟合时长拟合残差Fig.8 One hour time length fitting residuals for the 2nd day

对ISL体制下星地双向时间同步中的第1天弧段和第2天弧段的下行伪距和上行伪距分别分段进行高阶多项式拟合，第1天弧段下行伪距拟合残差RMS为0.053m，上行伪距拟合残差RMS为0.034m，如图9所示；第2天弧段下行伪距拟合残差RMS为0.055m，上行伪距拟合残差RMS为0.034m，可近似表征上下行测量噪声。则对上下行噪声进行合成，得到第1天弧段合成噪声约0.031m，对钟差的影响约为0.10ns，第2天弧段合成噪声约0.032m，对钟差的影响约0.11ns。将合成噪声分别与第1天和第2天的ISL体制下的星地双向时间同步结果按1小时拟合时长拟合的残差进行比较，可知本例中ISL体制下的星地双向时间同步结果拟合残差均大于合成噪声，其中第1天弧段的拟合残差超过合成噪声约0.11ns，第2天弧段的拟合残差略大于合成噪声，超过合成噪声约0.04ns，表明第1天弧段含有更大的系统误差。

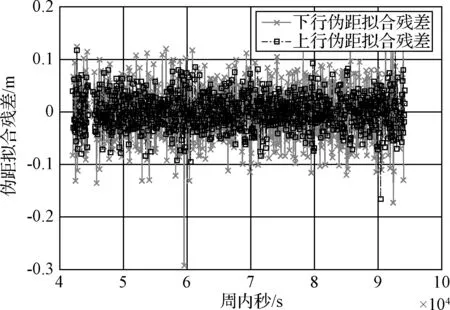
图9 第1天弧段伪距拟合残差Fig.9 Fitting residuals of pseudorange for the 1st day

为进一步分析ISL体制下的星地双向时间同步结果性能，计算第1天弧段和第2天弧段结果的阿伦方差，进行短期频率稳定度分析，结果如图10所示。第1天弧段和第2天弧段100s、1000s和1000s的频率稳定度见表1。

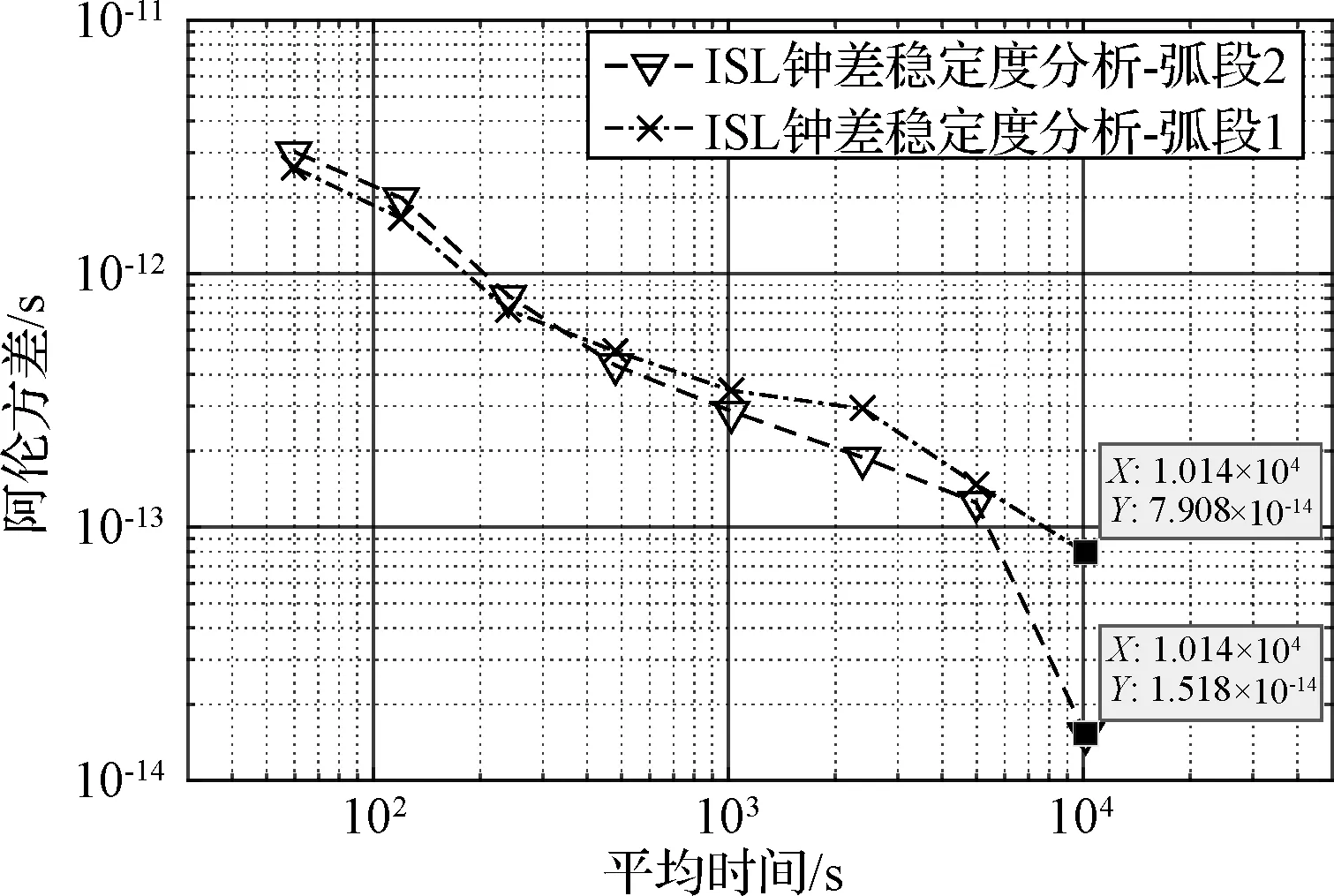
图10 星间链路体制下星地双向时间同步结果的频率稳定度分析Fig.10 Frequency stability of satellite-ground two-way time synchronization under ISL system

弧段100s1000s10000s第1天1．6×10-123．5×10-137．9×10-14第2天2．0×10-122．9×10-131．5×10-14

目前北斗2号卫星星地双向时间同步计算值短期频率稳定度[14]中10000s稳约为1×10-13，与之相比本文针对I1S卫星ISL体制下的星地双向时间同步结果较优；经过载波相位方法计算得到的北斗2号卫星钟差的频率稳定度[15]的10000s稳为4.3×10-14～1.5×10-13，与之相比ISL体制下星地双向时间同步结果的10000s稳定度在同一量级。结果表明ISL体制下星地双向时间同步结果的10000s稳优于8.0×10-14，最优可达1.5×10-14。

3 结 论

本文推导了星间链路体制下的星地双向时间同步数学模型，计算了在轨试验期间I1S卫星与地面站的相对钟差，并对计算结果分别按1周、1天和1小时时长进行参数拟合，最后进行短期频率稳定度分析，依据有限的数据计算结果，主要有以下结论：

1)对于1周拟合时长，ISL体制下的星地双向时间同步结果的拟合精度达3.42ns，与L波段结果的钟速差为-7.4×10-14，二者拟合残差具有一致性；

2)对于1天拟合时长，ISL体制下的星地双向时间同步结果能达到约0.30ns的拟合精度；

3)对于1小时拟合时长，ISL体制下的星地双向时间同步结果能达到约0.15ns的拟合精度；

4)分析ISL体制下的星地双向时间同步结果的短期稳定度，结果表明其10000s稳定度优于8×10-14。

[1] 王冬霞, 辛洁, 薛峰, 等.GNSS星间链路自主导航技术研究进展及展望[J]. 宇航学报, 2016, 37(11): 1279-1288. [WangDong-xia,XinJie,XueFeng,etal.DevelopmentandprospectofGNSSautonomousnavigationbaseoninter-satellitelink[J].JournalofAstronautics, 2016, 37(11): 1279-1288.]

[2] 黄波, 胡修林. 北斗 2 导航卫星星间测距与时间同步技术[J]. 宇航学报, 2011, 32(6): 1271-1275. [HuangBo,HuXiu-lin.Inter-satelliterangingandtimesynchronizationtechniqueforBD2[J].JournalofAstronautics, 2011, 32(6): 1271-1275.]

[3] 黄飞江, 卢晓春, 吴海涛, 等. 基于星间距离变化的动态双向时间同步算法[J]. 武汉大学学报: 信息科学版, 2010,35(1): 13-16. [HuangFei-jiang,LuXiao-chun,WuHai-tao,etal.Analgorithmofdynamictwo-waytimetransferbasedoninter-satelliterangevariation[J].GeomaticsandInformationScienceofWuhanUniversity, 2010,35(1): 13-16.]

[4] 孙文超, 常青, 徐勇, 等. 星间DOWRT中的相对论效应分析与修正[J]. 北京航空航天大学学报, 2012, 38(3): 335-339. [SunWen-chao,ChangQing,XuYong,etal.Analysisandcorrectiononrelativisticeffectofinter-satellitesusingdualone-wayranging/timesynchronization[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2012, 38(3): 335-339]

[5]LiuL,ZhuLF,HanCH,etal.Themodelofradiotwo-waytimecomparisonbetweensatelliteandstationandexperimentalanalysis[J].ChineseAstronomyandAstrophysics, 2009, 33(4): 431-439.

[6] 李瑞锋, 王元明. 星地双向时间同步技术在COMPASS中的应用[J]. 武汉大学学报: 信息科学版, 2013, 38(7): 842-844. [LiRui-feng,WangYuan-ming.Applicationoftwo-waysatellite-groundtimesynchronizationinCOMPASS[J].GeomaticsandInformationScienceofWuhanUniversity, 2013, 38(7): 842-844]

[7] 黄飞江, 卢晓春, 刘光灿,等. 星地动态双向时间同步与测距算法[J]. 宇航学报, 2014, 35(9):1050-1057. [HuangFei-jiang,LuXiao-chun,LiuGuang-can,etal.Analgorithmfordynamicsatellite-groundtwo-waytimesynchronizationandranging[J].JournalofAstronautics. 2014, 35(9):1050-1057].

[8]ChunhaoH,ZhiwuC,YutingL,etal.TimesynchronizationandperformanceofBeiDousatelliteclocksinorbit[J].InternationalJournalofNavigationandObservation, 2013, 2013.

[9] 谢钢. 全球导航卫星系统原理-GPS, 格洛纳斯和伽利略系统[M]. 北京: 电子工业出版社,2013:256-259.

[10] 武文俊, 李志刚, 杨旭海,等. 卫星双向时间频率传递中的Sagnac效应[J]. 宇航学报, 2012, 33(7):936-941. [WuWen-jun,LiZhi-gang,YangXu-hai,etal.Sagnaceffectontwo-waysatellitetimeandfrequencytransfer[J].JournalofAstronautics, 2012, 33(7):936-941.]

[11] 刘丽丽, 王跃科, 陈建云, 等. 导航星座自主时间基准的相对论效应[J]. 宇航学报, 2015,36(4): 470-476. [LiuLi-li,WangYue-ke,ChenJian-yun,etal.Effectsofrelativityinautonomoustimereferencefornavigationconstellation[J].JournalofAstronautics, 2015,36(4): 470-476.]

[12]WeissM,AshbyN.Globalpositioningsystemreceiversandrelativity[J].NISTtechnicalnote, 1999 (1385): 1-46.

[13] 李庆扬. 数值分析(第五版)[M]. 北京：清华大学出版社, 2008:23-26.

[14]ZhouSS,HuXG,LiuL,etal.Applicationsoftwo-waysatellitetimeandfrequencytransferintheBeiDounavigationsatellitesystem[J].ScienceChinaPhysics,Mechanics&Astronomy, 2016, 59(10): 78-86.

[15]HauschildA,MontenbruckO,SteigenbergerP.Short-termanalysisofGNSSclocks[J].GPSsolutions, 2013, 17(3): 295-307.

通信地址：陕西省西安市临潼区书院东路3号(710600)

E-mail:lvhongchun123@163.com

A Method of Two-Way Satellite-Ground Time Synchronization Under Inter-Satellite Links System

LV Hong-chun1.2,3, LU Xiao-chun1,3,4, WU Jian-feng1,3,5

(1. National Time Service Center, Chinese Academy of Sciences, Xi’ an 710600, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China; 3. Key Laboratory of Precision Navigation and Timing Technology, Chinese Academy of Sciences, Xi’an 710600, China; 4. School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 101408, China; 5. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 101408, China)

The mathematical model of the two-way satellite-ground time synchronization is deduced, the method of the two-way satellite-ground time synchronization under inter-satellite links system is proposed, and the relative satellite-ground clock offset of the new-generation BeiDou navigation satellite and the Xi’an station during the orbit test is calculated. The parameters are fitted by the time length of 1 week, 1 day and 1 hour, respectively, and the short-term frequency stability analysis is performed, which verifies the accuracy and performance of the two-way satellite-ground time synchronization of inter-satellite links mode in the experimental stage, and the limited data shows that under the fitting time of 1 week, 1 day and 1 hour, the accuracy of the two-way satellite-ground time synchronization of inter-satellite links mode are up to 3.42 ns, 0.30 ns and 0.15 ns, respectively. And the 10000 s frequency stability is better than 8×10-14.

Inter-satellite links (ISL); Satellite-ground time synchronization; Time-division; BeiDou navigation satellite system (BDS)

2017-03-20;

2017-05-09

P228.4

A

1000-1328(2017)07-0728-07

10.3873/j.issn.1000-1328.2017.07.000

吕宏春(1986-)，男，博士生，主要从事卫星导航定位方法与技术的研究。