基于RLC/RC模型的火花能量计算方法研究

杨 顺,王志宇,杨遂军,叶树亮

(中国计量大学 计量测试工程学院 工业与商贸计量技术研究所,浙江 杭州 310018)

粉尘燃爆事故频发,对人民群众生命财产造成重大损失[1-3]。最小点火能量(Minimum Ignition Energy)是粉尘燃爆危险评价中的一个重要参数,它表明能够点燃粉尘云的最低火花能量[4]。在目前的测试标准中,如EN 13821、ASTM E2019-03、ISO/IEC 80079等,计算火花能量最简单的方法是基于电容的能量计算公式0.5CU2[5-7]。但由于外部电路损耗、电磁辐射、电晕放电等影响,火花能量小于电容中存储的能量[4]。更精确的方法是通过放电火花的电压与电流的乘积对时间进行积分计算火花能量。由于电压与电流相位存在偏差,若未修正电压与电流之间的相位偏差,会导致能量计算结果不准确[8]。许多研究数据表明,欧姆定律可应用于火花能量计算,通过火花电流的平方与火花电阻的乘积对时间进行积分计算火花能量[9-10]。因此,只需测量火花通道的电流,求解出火花电阻,即可计算火花能量。

张云明等[11]利用指数衰减的正弦周期性振荡函数拟合法对实际电流曲线进行拟合,结果验证了火花放电持续时间内火花电阻不变的假设。刘佳[8]利用指数衰减正弦公式对不同电容下的实际电流曲线进行拟合,结果表明在放电后期拟合曲线与实际电流曲线在幅值和周期上存在一定的误差,这是由于火花电阻是动态变化的原因引起的。任纯力[12]、鲁林[13]利用龙格-库塔法模拟了火花放电过程中火花电阻的变化过程,结果表明火花间隙被击穿后,火花电阻急剧下降,当火花电流值很低时,火花电阻急剧增加,直到放电结束。Wang等[14]建立了一个包含可变火花电阻与火花电感的等效放电模型,结果表明火花电阻与火花电感随放电时间呈指数关系。上述作者虽发现了火花电阻与火花电感的时变特性,但在实际计算放电能量时仍采用固定火花电阻与火花电感。

为了实现火花能量更精确的计算,建立一种包含可变火花电阻与火花电感的等效放电模型,搭建一种宽放电能量范围的静电火花发生装置,对比不同放电能量下拟合曲线与实际放电曲线差异,验证该模型在静电火花能量计算方法上的可行性。

1 火花的产生与测量

1.1 火花的产生

静电火花的产生原理是通过高压电源对储能电容进行充电,当充电完成后,将储能电容上的电压加载到电极两端,如果电极两端的电压达到电极间隙气体的击穿电压时,电极间隙气体将发生强烈电离,形成电离通道,并产生火花放电现象。

本文搭建的静电火花发生装置原理如图1。其中,高压电源用于提供10 kV充电电压;充电继电器用于控制充电回路的导通与断开;充电电阻阻值为10 MΩ,用于限制充电电流不超过1 mA;储能电容用于存储充电能量;选择继电器1、2用于选择不同阻值的放电回路,以模拟不同的火花放电情形。其中,采用额外串联电阻情况下的静电放电方式可用于模拟人体静电放电情形,测试电火工品对模拟人体静电的感度,为设计用于生产和使用电火工品的系统提供静电防护数据。串联电阻的标称阻值为5 kΩ;放电继电器用于控制放电回路的导通与断开;高压电极和地电极均采用钨材料制成,直径2 mm,电极间距4 mm。

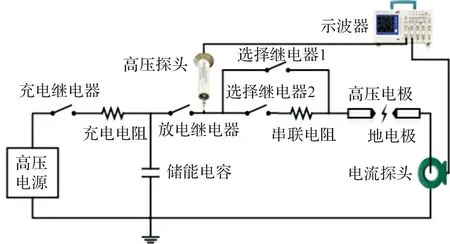
图1 放电电路示意图Figure 1 Schematic diagram of discharge circuit

1.2 火花的测量

为计算火花放电能量,需测量回路放电电压与电流。如图1,在放电继电器端放置一个高压探头(Tektronix P6015),用于测量放电电压;在地电极端放置一个电流探头(Pearson 150),用于测量放电电流。根据电流的输出大小,使用0 dB、20 dB、40 dB的衰减器来满足示波器的输入要求。将高压探头与电流探头接入示波器(Tektronix TDS 2024C)进行数据采集。UI积分法计算的放电能量可通过电压与电流的乘积对时间进行积分计算。

不同放电情形时的放电电压与放电电流曲线如图2。当放电回路未采用额外串联电阻时,放电曲线如图2(a),为欠阻尼衰减振荡状态。当放电回路采用额外串联电阻时,放电曲线如图2(b),为过阻尼状态。

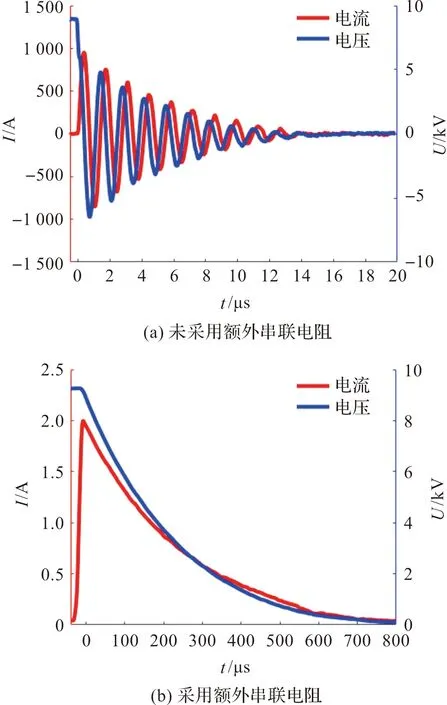
图2 不同放电情形时的放电波形Figure 2 Discharge waveforms for different discharge scenarios

2 等效模型建立

2.1 RLC模型

当放电回路未采用额外串联电阻时,火花放电过程基本符合二阶RLC电路零输入响应的欠阻尼振荡状态。因此,基于图1所示的放电电路,建立了一种包含可变火花电阻与火花电感的等效RLC放电模型,如图3所示。其中,C为储能电容,Rc为回路电阻,主要为放电继电器与选择继电器1的电阻,Lc为回路电感,为充放电电路固有参数,火花电阻Rs与火花电感Ls为火花间隙等效参数。

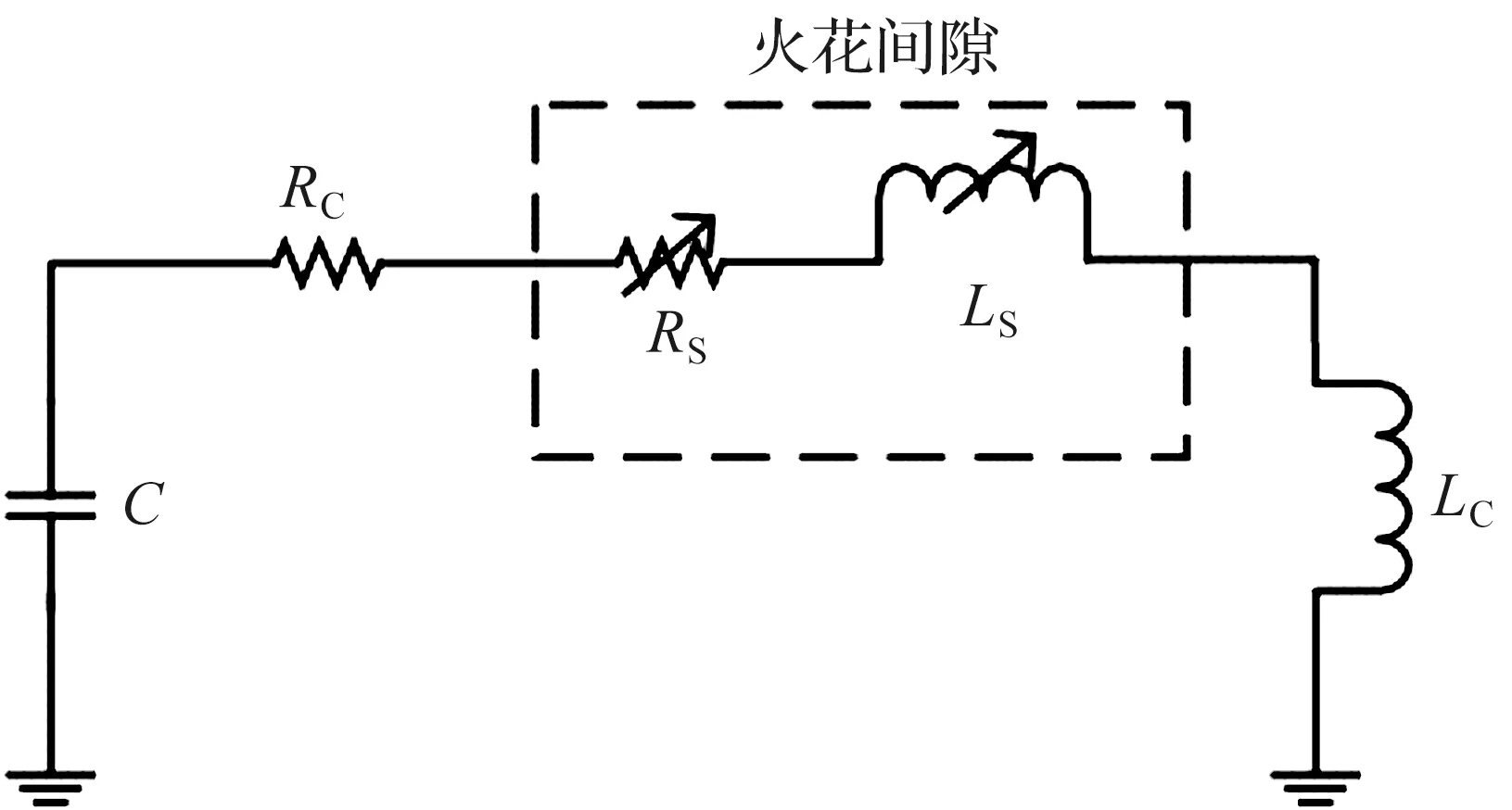
图3 等效RLC模型Figure 3 Equivalent RLC model

为了便于表示,Rtotal=Rc+Rs,Ltotal=Lc+Ls,根据基尔霍夫定律,放电回路存在式(1)关系[14-15]:

(1)

根据初始条件i(0)=0,U0=Ltotaldi/dt|t=0,可求出电流表达式如式(2):

(2)

其中,U0为充电电压,β为衰减因子,ω为角频率,β与ω表达式如式(3)、(4):

(3)

(4)

假设火花电阻与火花电感随时间呈指数变化[14],如式(5)、(6):

Rs=aebt+c,

(5)

Ls=ment。

(6)

其中,常数c是当电极间隙中的空气被电离时火花通道的电阻,系数a、b、m、n通过实验来确定。

2.2 RC模型

当放电回路采用额外串联电阻时,火花放电过程基本符合二阶RLC电路零输入响应的过阻尼非振荡状态。由于放电回路电感值非常小,且相对于放电回路电阻可忽略不计。因此,将火花放电过程简化为RC电路的零输入响应过程。基于图1所示的放电电路,建立了一种包含可变火花电阻的等效RC放电模型,如图4。其中,C为储能电容,Rc为回路电阻,主要是标称阻值为5 kΩ的串联电阻,火花电阻Rs为火花间隙等效参数。

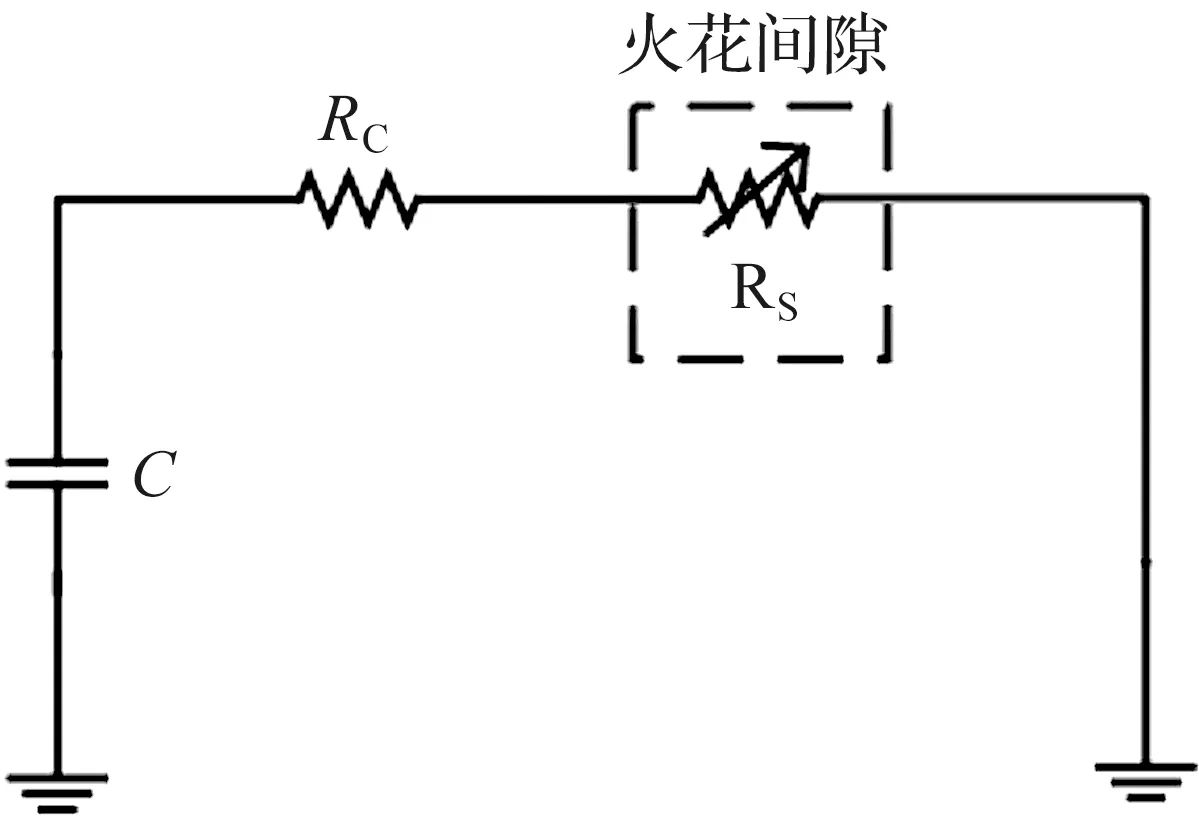
图4 等效RC模型Figure 4 Equivalent RC model

为了便于表示,Rtotal=Rc+Rs,根据基尔霍夫定律,放电回路存在式(7)关系:

(7)

根据初始条件U(0)=U0,i(0)=U0/Rtotal,可求出电流表达式如式(8):

(8)

其中,U0为充电电压,β为衰减因子,β表达式如式(9):

(9)

由于在火花放电起始阶段火花电阻维持不变,且相对于回路电阻可忽略。因此,假设火花电阻随时间呈指数变化如式(10):

Rs=deft。

(10)

系数d、f通过实验来确定,表示火花电阻随时间的变化趋势。

3 结果与分析

3.1 实验说明

为验证基于时变RLC/RC模型的静电火花能量计算方法的可行性,分别进行以下实验:

1)在未采用额外串联电阻条件下,分别以充电电容为22 nF、34 nF、52.35 nF,充电电压为10 kV,进行静电火花放电实验。每个条件下重复进行五次实验,避免随机误差;

2)在采用额外串联电阻条件下,分别以充电电容为52.35 nF、122 nF、222 nF,充电电压为10 kV,进行静电火花放电实验。每个条件下重复进行五次实验,避免随机误差。

在建立等效放电模型之前,需根据电流波形求解放电回路总电阻与总电感。在未采用额外串联电阻条件下,通过波形的振荡频率与振幅衰减求解衰减因子β与角频率ω,则放电回路总电感Ltotal=1/(ω2C),放电回路总电阻Rtotal=2βLtotal;在采用额外串联电阻条件下,根据电流波形找出电流最大值imax,则放电回路总电阻Rtotal=U0/imax,衰减因子β=1/(RtotalC)。

实际回路电阻与回路电感通过LRC测试仪(Keysight E4980AL)测量。由于放电频率会影响回路电阻与回路电感,因此,在测量回路电阻与回路电感时,需将测量频率调整至实际放电频率。在未采用额外串联电阻条件下,放电频率约500 kHz,将测量频率调整至500 kHz,测量结果如表1。

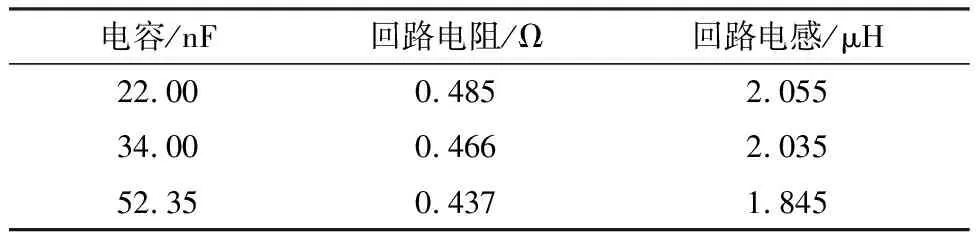
表1 回路电阻与电感Table 1 Circuit resistance and inductance

采用额外串联电阻条件下,以200 kHz步长频率分别测量不同频率下的回路电阻,测量结果如图5。从图中可以看出,回路电阻随测量频率的提高而减小,然而,实际放电频率未知,无法通过扫频实验测出实际放电频率下的回路电阻。由于在火花放电起始阶段火花电阻维持不变,且相对于回路电阻可忽略,因此,可将此时的Rtotal等效为回路电阻。

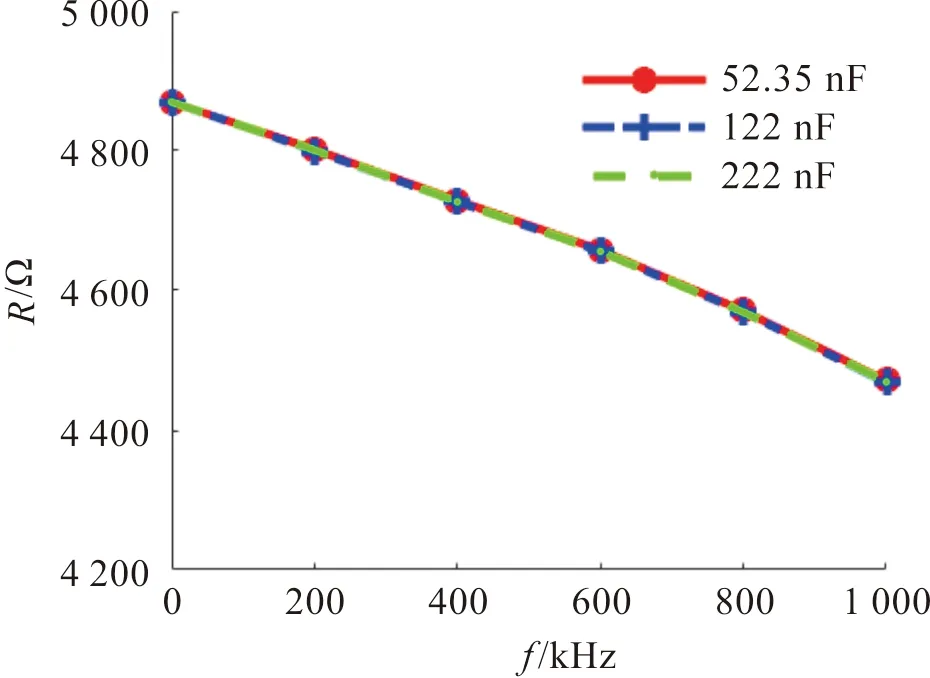
图5 回路电阻随测量频率的变化情况Figure 5 Variation of circuit resistance with measurement frequency

3.2 欠阻尼情况

在未采用额外串联电阻条件下,实际电流曲线如图6红色曲线所示,为欠阻尼状态。当火花电阻与火花电感作为一个常数来拟合电流曲线时,总电感Ltotal等于回路电感Lc,总电阻Rtotal包括回路电阻Rc和火花电阻Rs表达式(5)中的常数项c。常数项c由存储能量、输入电压、电极间隙、环境湿度等决定[14,16]。回路电阻Rc使用LRC测试仪测量,测量结果如前表1。拟合曲线如图6绿色曲线所示,在放电末期拟合曲线的振荡频率快于测量曲线、振幅衰减慢于测量曲线,这意味着在放电过程中不适合使用固定火花电阻和固定火花电感来拟合电流曲线。

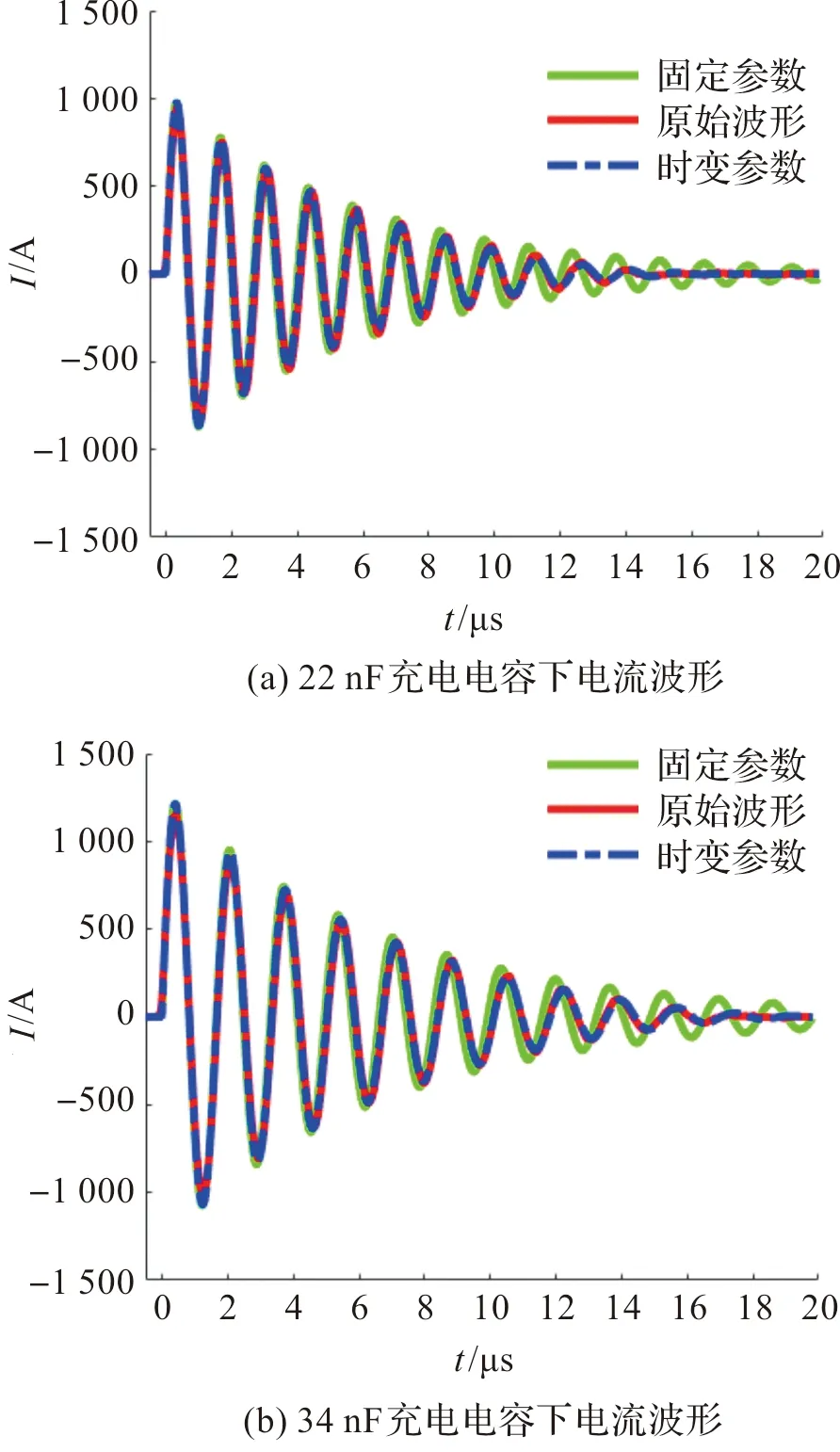
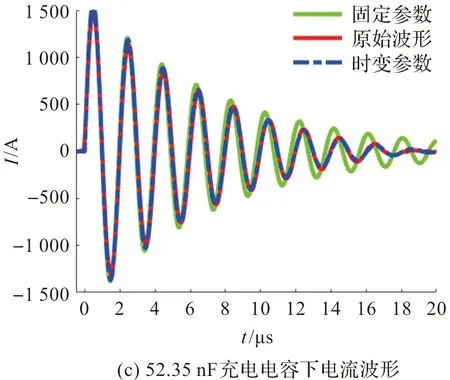
图6 欠阻尼波形Figure 6 Underdamped waveform

为了得到较好的拟合效果,采用时变火花电阻与火花电感来拟合电流曲线。火花电阻与火花电感分别满足式(5)、(6)关系,其中系数m和n影响火花中后期的振荡频率,系数a和b影响火花中后期的振幅衰减。通过调整系数,可以使得拟合曲线与实际电流曲线之间具有很好的一致性。拟合系数的调整依据拟合优度R2计算,即拟合曲线相对于实际曲线的拟合程度。采用确定系数R2来判断拟合程度,本文以确定系数R2大于0.95为阈值来调整拟合系数。拟合曲线如图6蓝色曲线所示,拟合参数值如表2。

表2 RLC模型拟合参数值Table2 Fitting parameter values of RLC model

3.3 过阻尼情况

在采用额外串联电阻条件下,实际电流曲线如图7红色曲线所示。当回路总电阻作为一个常数来拟合电流曲线时,回路总电阻Rtotal阻值为4 700 Ω。拟合曲线如图7绿色所示,从图中可以看出,拟合曲线衰减慢于测量曲线,且随着放电能量的增加,拟合曲线与实际放电曲线的偏差增大。同样意味着在放电过程中不适合使用固定火花电阻来拟合电流曲线。

为了得到较好的拟合效果,采用时变火花电阻来拟合电流曲线。火花电阻满足式(10)关系,通过调整系数,可以使得拟合曲线与实际电流曲线在放电前期具有很好的一致性,而在放电后期同样也会存在偏差。拟合系数的调整依据拟合优度R2计算,即拟合曲线相对于实际曲线的拟合程度。采用确定系数R2来判断拟合程度,本文以确定系数R2大于0.95为阈值来调整拟合系数。拟合曲线如图7蓝色曲线所示,拟合参数值如表3。

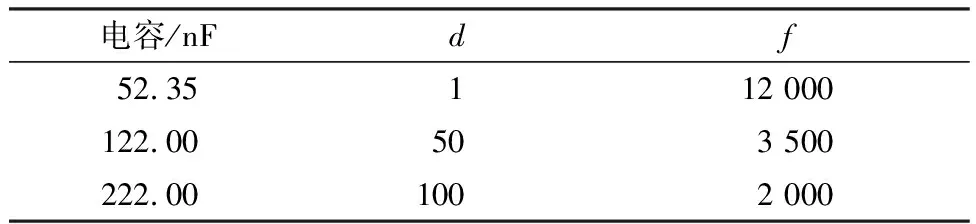
表3 RC模型拟合参数值Table3 Fitting parameter values of RC model

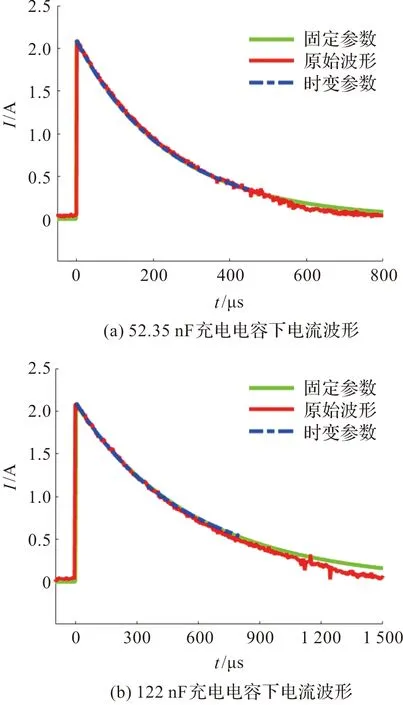
图7 过阻尼波形Figure 7 Overdamped waveform

通过放电电压除以放电电流计算回路总电阻,分析回路总电阻的变化情况。不同能量下的回路总电阻随时间变化情况如图8。在放电前期,电极间隙间形成稳定的火花通道,火花电阻基本保持不变。随着放电的进行,维持火花通道的能量逐渐降低,火花电阻缓慢增大。直到放电后期,放电能量难以维持火花通道,此时火花通道极不稳定,火花电阻迅速增大,直至无法形成火花通道,放电结束。

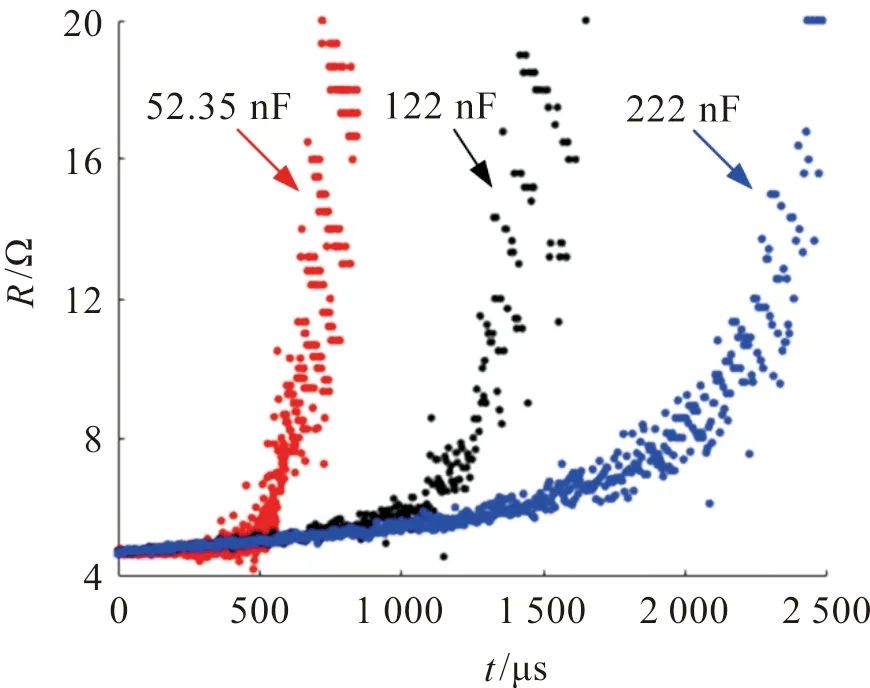
图8 回路总电阻随时间的变化情况Figure 8 Change of total circuit resistance with time

3.4 能量计算结果与对比分析

在欠阻尼情况下,对比分析拟合能量与UI积分法计算的放电能量之间的偏差。拟合能量通过I2R积分法计算。拟合能量按照火花电阻与火花电感的性质分为两种情况:一种是固定参数拟合能量,即火花电阻与火花电感作为常数进行拟合计算的放电能量;另一种是时变参数拟合能量,即火花电阻与火花电感作为时变值进行拟合计算的放电能量。能量计算结果如表4,固定参数拟合能量相对于UI积分法计算的放电能量偏差在0.9%～5.6%范围内。这是由于在放电后期火花电阻迅速增大,实际电流曲线衰减快于拟合曲线的原因造成的。时变参数拟合能量与UI积分法计算的放电能量偏差在0.6%～3.2%范围内,相对于固定参数拟合能量更精确。

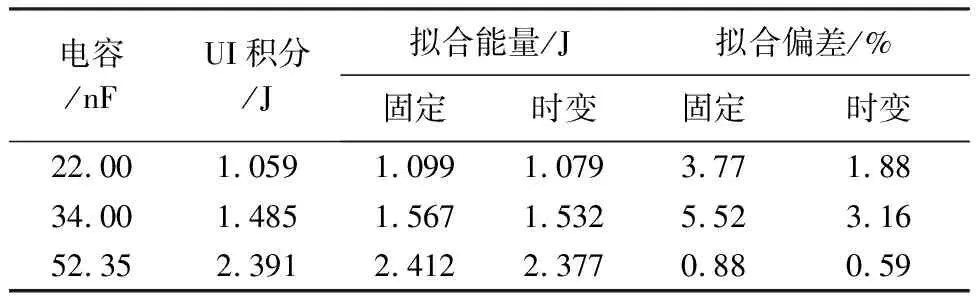
表4 欠阻尼能量计算结果Table 4 Underdamped Energy calculation results

在过阻尼情况,由于火花电阻的变化趋势不稳定,无法通过时变参数拟合出整体很好的效果。为了分析火花间隙形成稳定火花通道时间段内放电能量占全部放电能量的比例。将火花电阻从缓慢上升阶段到急速上升阶段的过渡时刻作为分界点,分界点之前时间段认为是形成稳定的火花通道,分界点之后时间段认为火花通道不稳定。分别计算分界点之前时间段内的放电能量和全部放电能量,能量计算方式通过UI积分法计算,能量计算结果如表5。从表中可以看出,在火花间隙形成稳定火花通道时间段内放电能量占全部放电能量比例约95%,此时可忽略火花通道不稳定时间段内的放电能量。

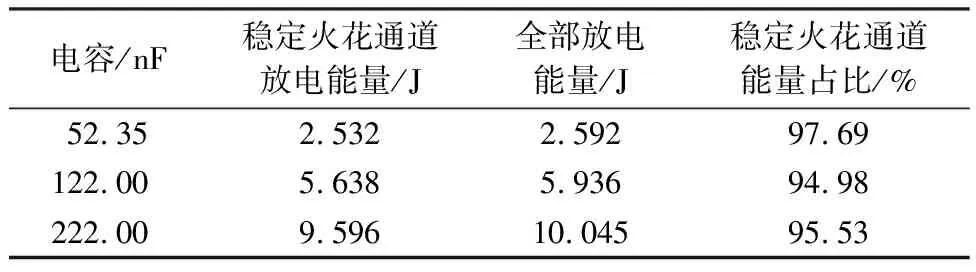
表5 稳定火花通道能量占比Table 5 Energy proportion of stable spark channel

同时,对比分析形成稳定火花通道时间段内拟合能量与UI积分法计算的放电能量之间的偏差。能量计算结果如表6,52.35 nF与122 nF充电电容情况下,时变参数拟合能量相对于固定参数拟合能量更加精确;222 nF充电电容情况下,时变参数拟合能量计算误差增大。这是因为随着充电能量的增加,放电时间延长,形成稳定火花通道的时间段延长,在形成稳定火花通道的时间段后期,时变参数拟合的火花电阻偏小,最终导致拟合能量误差增大。时变参数拟合能量与UI积分法计算的放电能量偏差在0.2%～4.3%范围内。

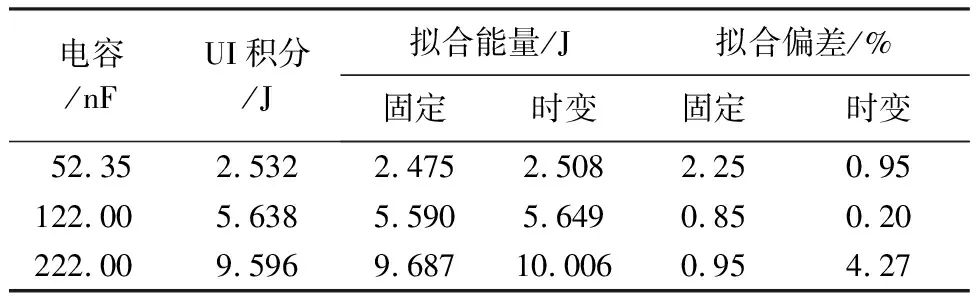
表6 过阻尼能量计算结果Table 6 Overdamped Energy calculation results

4 结 论

本文通过建立一种包含可变火花电阻与火花电感的等效RLC/RC静电放电模型,搭建一种宽放电能量范围的静电火花发生装置,对比分析不同能量下的拟合曲线与实际放电曲线的差异,验证了该模型在静电火花能量计算方法上的可行性。

实验结果表明,在欠阻尼情况下,放电后期火花电阻与电感迅速增大,导致实际电流曲线衰减快于拟合曲线。同时,时变参数拟合能量与UI积分能量偏差在0.6%～3.2%范围内,相对于固定参数拟合能量更加精确。在过阻尼情况下,放电前期,电极间隙间形成稳定的火花通道,火花电阻基本保持不变。随着放电的进行,维持火花通道的能量逐渐降低,火花电阻逐渐增大。直到放电后期,放电能量难以维持火花通道,此时火花通道极不稳定,火花电阻迅速增大,直至无法形成火花通道,放电结束。同时,形成稳定火花通道时间段内放电能量约占全部放电能量的95%,可忽略火花通道不稳定时间段内的放电能量。且在形成稳定火花通道时间段内,时变参数拟合能量与UI积分能量偏差在0.2%～4.3%范围内。