单向航道下连续泊位分配与船舶调度集成优化

吴云强，张 戎

同济大学 城市交通研究院 道路与交通工程教育部重点实验室 上海市轨道交通结构耐久与系统安全重点实验室，上海201804

随着海上运输业的迅猛发展，集装箱港口在全球货运体系中的地位逐渐提高。港口中泊位与航道等核心作业资源的分配或调度直接影响其服务水平，并关乎整个港口的运营成本。然而，进出港时间的限制以及泊位与航道复杂的协作关系使得二者集成优化变得格外复杂。因此，如何根据现实情况，快速制定考虑航道资源的船舶调度方案与泊位分配计划，成为集装箱港口领域研究的热点问题之一。

在考虑航道资源的船舶调度研究方面，现有文献主要关于单向、双向以及复式航道。针对单向航道，徐国裕等[1]考虑船舶优先级，以船舶载重吨、吃水深度等因素为指标，通过工作排序方法获得船舶进出港次序。邬惠国等[2]基于多目标格序决策理论，构建通航方案评价指标体系，并采取熵值法计算各个指标的权重，从而选取最佳船舶进出港方案。郑红星等[3]考虑安全行驶距离与大型船舶需要在潮汐时段进出港口的作业规则，以所有船舶作业等待时间之和最小为优化目标，并采用改进和声搜索算法来求解。对于双向航道，Eduardo等[4]考虑碳排放和潮汐等因素，以所有船舶等待时间之和最小为目标函数，构建了混合整数规划模型，并设计了模拟退火算法，且通过多组算例来验证其求解效率。张新宇等[5]考虑单向通航与双向通航之间的转换问题，保证船舶在航道安全和高效行驶，以降低停留时间与调度时间为目标，构建了混合整数线性规划模型，且采用改进遗传算法来求解问题。对于复式航道，陈向[6]考虑船舶类型与在港航行速度的影响，基于文献[5]来建立混合整数规划模型，并结合问题特征，采用相应启发式算法进行求解，得到最佳泊位分配与船舶调度方案。这些研究大多关于单向航道，有关双向和复式航道研究较少，但由于单向航道中进出港时段交替进行，单向航道下的船舶调度问题比双向航道更为复杂，且单向航道是复式航道的基础。绝大多数文献考虑船舶优先级和潮汐等因素，以港口实际作业情况为约束条件，采取方案评价法或优化算法来获取最佳船舶进出港方案，但几乎没有文献考虑进出港时段对船舶调度的影响。

泊位分配问题基于泊位类型可分为离散泊位分配与连续泊位分配，且考虑计划期开始时刻船舶是否已经停靠在锚地，可分为静态泊位分配问题与动态泊位分配问题。依据两两组合原理，泊位分配问题可分为四类，其中动态连续泊位分配问题最为复杂，另外三类问题已有国内外众多学者开展了大量的研究[7-14]。针对动态连续泊位分配问题，秦天保等[15]基于约束规划理论，以所有船舶在港停留时间之和最小为目标函数，构建了混合整数规划模型，并利用CPLEX来解决此问题，且通过算例实验来分析算法求解效率。曾庆成等[16]针对港口作业中的不确定性因素，分别以延误时间之和最小与鲁棒性指标最大为第一、二阶段目标函数，最后设计了改进拉格朗日松弛算法。Ursavas[17]考虑船舶服务的优先级，通过动态离散事件仿真模型来建立泊位分配决策支持系统，并嵌入优化算法确定各船舶的优先级，从而帮助港口制定战略层与战术层的决策。Liu等[18]考虑作业环境的不确定性，以最差条件下的运营成本最小为目标函数，构建了相应的两阶段数学模型，并通过启发式算法来解决大规模调度问题。从上可知，现有学者对于动态连续泊位分配的研究主要考虑船舶到港时间或者优先级，以计划期内船舶在港停留时间之和最小为目标函数，构建相应的数学规划模型，并通过启发式算法或精确算法进行求解，但少有文献涉及潮汐因素对泊位分配的影响。

在泊位分配与船舶调度集成优化研究方面，以船舶待停靠泊位已知为前提，Zhang 等[19]根据港口不同区域交通流，以在港等待时间最小为目标函数，构建了相应数学规划模型，结合模拟退火算法的相关原理来构造求解算法。Jia等[20]考虑内锚地影响，以到港船舶时间惩罚成本之和最小为目标函数，构建了混合整数规划模型，并结合拉格朗日松弛来求解此问题。以船舶待停靠泊位未知为前提，郑红星等[21]考虑泊位类型的差异化，以计划期内船舶成本之和最小为目标函数，构建了混合整数线性规划模型，并采用改进声搜索算法来求解。上述文献主要是在船舶待停靠泊位已知的情况下，根据离散泊位作业情况，以降低船舶在港停留时间为目标，研究泊位分配与船舶调度协同优化，罕有学者考虑连续泊位对集成优化的影响和采用精确算法求解。

综上，现有文献关于船舶调度方面较多，动态连续泊位分配次之，泊位分配与船舶调度集成优化最少，后者为港口调度领域关键问题之一。然而，针对泊位分配与船舶调度集成优化问题，大部分研究都假设船舶待停靠泊位已知，只是得到船舶进出港的最佳时刻，此时已有泊位分配方案未必最佳，实际上应根据船舶调度与泊位分配交互影响来制定最佳泊位分配方案与船舶进出港时刻表；同时，现如今大多数港口的泊位为连续泊位，连续泊位分配是一个以时间与岸线为维度的二维装箱问题，当其与船舶调度问题结合时，由于后到港船舶可能因船长因素而先进港，从而改变进出港次序，进而改变前到港船舶靠泊位置，使问题变得尤为复杂，增加了求解难度；除此之外，现有文献大都基于启发式算法或仿真方法来解决二者集成优化问题，罕有采用具有较强理论支撑的优化理论和精确算法。

因此，本文研究动态连续泊位分配与船舶调度集成优化问题，从降低港口成本的视角出发，重点考虑潮汐与进出港时段对集成优化的影响，兼顾单向航道的作业特点，并设计效果较好的精确算法进行求解，最终制定固定计划期内各艘船舶最佳泊位分配方案和进出港时序。

1 问题描述

在预知船舶抵港计划、配载计划后，港口会为其制定靠泊计划与作业计划。当船舶抵达港口后，其将停靠在锚地，直至得到VTS 中心允许起锚指令后，船舶通过航道行驶至对应泊位，并在此完成装船或者卸船作业；当船舶提出离港申请后，港口会把此艘船舶的船名、靠泊位置等信息发送到VTS 中心审核，直到船舶得到可以离港的通知后，才可通过航道行驶出港口。从中可知，航道与泊位对港口作业效率有非常大的影响。

其中，考虑航道资源的船舶调度目的是在遵循航道管理的前提下，让船舶尽快通过航道，降低在港停留时间。现如今大多数港口受到航道宽度的限制，只能单向通过，异向行驶的船舶无法同时通行，即航道类型为单向航道。若不制定合适次序，将导致进港船舶一直停靠在锚地、出港船舶停泊在港池内，容易发生碰撞。同时，整个计划期可分为多个进港时段与出港时段，且时段交替进行，即船舶只能在进港时段完成进港过程，出港时段完成出港过程；此外，船舶在航行时前后之间须保持安全距离，以免发生追尾，且某些大型船舶需乘潮进出港口。

动态连续泊位分配指船舶不是计划期开始时就已停靠在锚地，而是在计划期内动态到达港口，且船舶的船头可选择岸线任意位置来停靠。同时，不同船舶靠泊位置与时间段不能同时存在重叠。泊位一般与港口后方堆场某些箱区匹配，即停靠此泊位的船舶都是通过上述箱区来装卸货物，从而产生偏好泊位。若船舶靠泊位置偏离偏好泊位，将会增加此艘船舶与堆存箱区间的距离，导致港口作业成本增加，被称为泊位偏离成本。此外，若船舶实际开始离港时刻晚于预计离港时刻，且这是由于港口作业安排造成的，则港口需要给船舶一定经济补偿，被称为船舶滞期成本。

因此，本文问题可描述为，针对单向航道的连续泊位集装箱港口，已知船舶预计到港时刻等信息，重点关注大型船舶需乘潮进出港口与进出港时段交替的作业现实，兼顾船舶靠泊的时空约束与航行时需保持安全距离的要求，以船舶滞期成本与泊位偏离成本之和最小为目标函数，确定每艘船舶的进港时刻、出港时刻与靠泊位置。

2 数学模型

2.1 假设条件

（1）船舶的船头均朝向岸线刻度为0的方向；（2）船舶进出港过程只能分别发生在进港时段与出港时段；（3）不涉及船舶具体装卸过程。

2.2 模型建立

模型所涉及到的参数、中间变量与决策变量如表1。

表1 符号说明Table 1 Symbol description

（1）目标函数

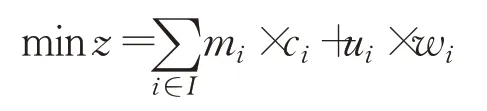
其中，mi×ci为泊位偏离成本；ui×wi为滞期成本，目标函数为所有船舶上述成本之和最小。

（2）约束条件

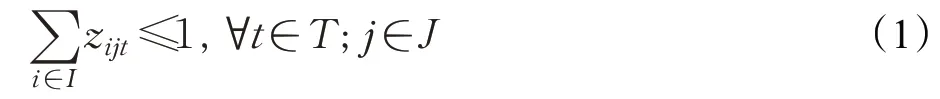
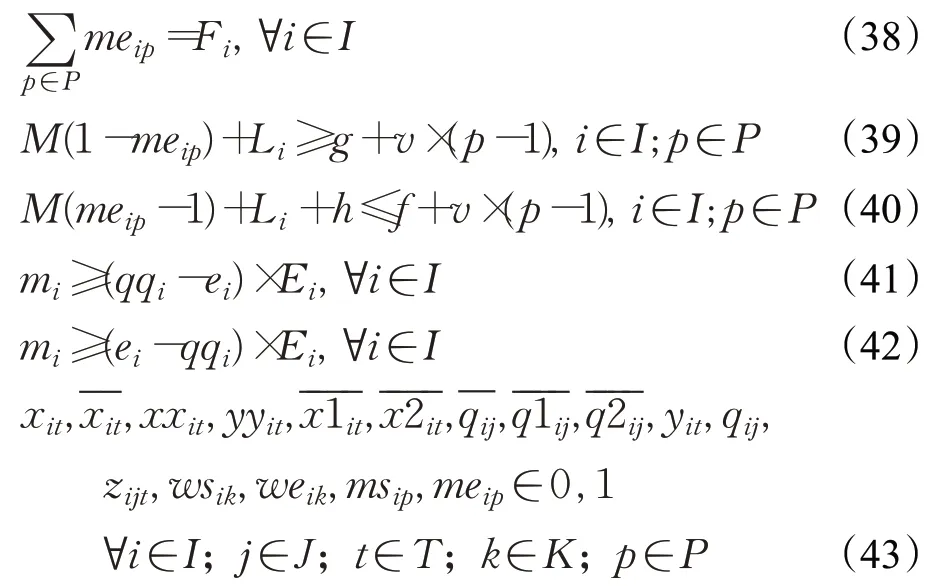
其中，式（1）表示各艘船舶选取的靠泊位置不能重合；式（2）、（3）表示船舶在航道航行时需保持安全距离；式（4）定义了变量xxit；式（5）定义了变量yyit；式（6）表示每艘船舶的船头需选择一个靠泊位置；式（7）表示每艘船舶靠泊位置不能超过岸线长度；式（8）定义了变量qqi；式（9）～（11）表示船舶开始进港时刻的相关约束；式（12）～（14）表示船舶开始离港时刻的相关约束；式（15）、（16）定义了变量ui；式（17）、（18）定义了变量；式（19）～（21）定义了变量；式（22）～（23）定义了变量；式（24）～（26）定义了变量；式（27）、（28）定义了变量zijt；式（29）表示每艘船舶需选择一个进港时段进行进港过程；式（30）、（31）表示船舶进港开始时刻与进港完成时刻需在时段范围内；式（32）表示每艘船舶需选择一个出港时段进行出港过程；式（33）、（34）表示船舶出港开始时刻与出港完成时刻需在时段范围内；式（35）表示乘潮船舶须选一个潮汐时段来完成进港；式（36）～（40）表示乘潮船舶进出港开始时刻与进出港完成时刻需满足的时间约束；式（41）、（42）定义了变量mi；式（43）表示变量取值范围。

3 Dantzig-Wolfe分解

通过观察上述混合整数线性规划模型，可知式（1）～（3）为耦合约束，其余约束具有对角分块结构，可针对每一艘船舶单独求解。因此，通过Dantzig-Wolfe 分解方法把上述数学模型分成一个主问题与子问题，每艘船舶对应一个子问题，且通过求解新模型得到的最优解为原问题最优解[22]。

3.1 主问题模型

为便于描述主问题，定义如表2所示符号。主问题模型如下所示：

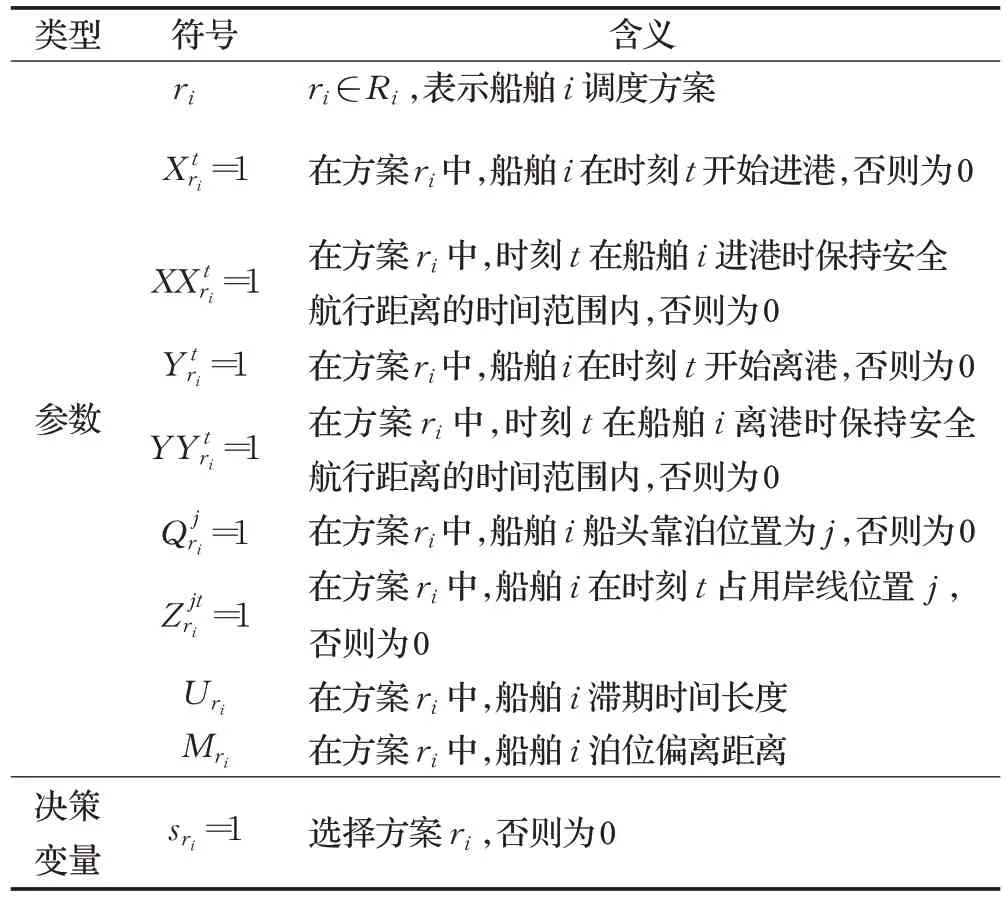
表2 主模型符号Table 1 Master model symbol

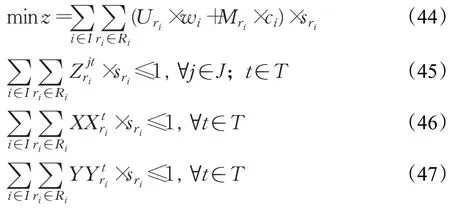
式（44）为目标函数，表示所有方案泊位偏离成本与滞期成本之和最小；式（45）表示所有方案中的船舶不能在同一时刻占用相同岸线位置；式（46）、（47）表示所有方案中的船舶在航道航行时需保持安全距离；式（48）表示任意一艘船舶需选择一个方案；式（49）表示变量sri的取值范围。由于可选的船舶调度方案数量较多，本文通过列生成算法求解主问题的松弛问题。在松弛掉0-1变量相关约束之后，即约束（49），其余的约束与目标函数构成列生成算法用到的主问题模型。

3.2 定价子问题模型

分别以π、μ、α、β当作约束（45）～（48）的对偶变量，则主问题检验数的表达式为：

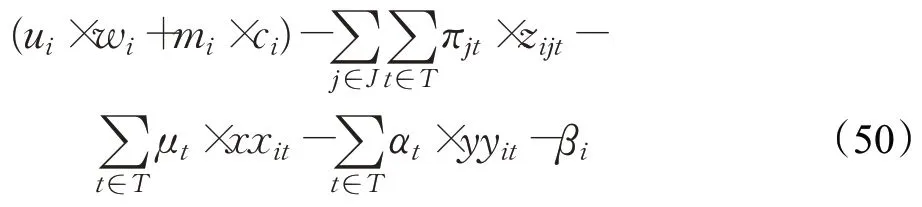
在列生成迭代过程中，子问题是寻找检验数小于0的列，并把它添加到主问题模型中，子模型为：

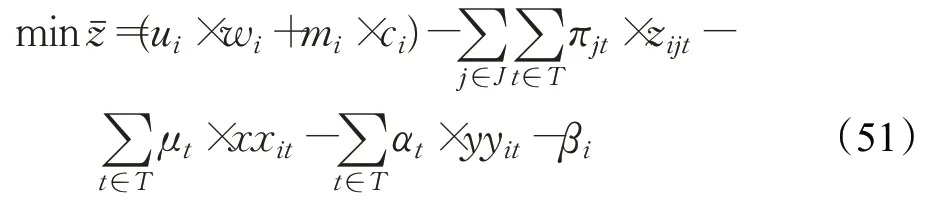
子问题约束条件为式（4）～（43）。

在每个子问题中，角标i不变，表示相应船舶，共有船舶数量个子问题。每个子问题对应一个船舶调度方案，其需满足靠泊位置与进出港时刻有关约束，且只有目标函数值小于0 的解对应的列才能加入主模型中迭代求解，如果没有满足条件的列，则已找到主问题松弛问题最优解。同时，根据对偶性质可知，对偶变量π、μ、α小于0，当β小于等于0时，主问题检验数大于等于0，此时不存在检验数小于0的列，则可不必对子问题进行求解。

4 算法设计

由于列生成只能得到原问题松弛问题的最优解，不能确保这个解为整数，因此将其与分支定界相结合，通过分支定价算法来求解此问题，如图1。对于根节点（原问题），根据初始解生成规则生成初始列加入主问题中，从而得到受限主问题，接着迭代求解主问题和子问题，获得松弛问题最优解。若此解满足整数约束，其是原问题最优解，否则，需分支。对于每个分支（子节点），通过列生成算法进行求解，直到找到原问题可行最优解。

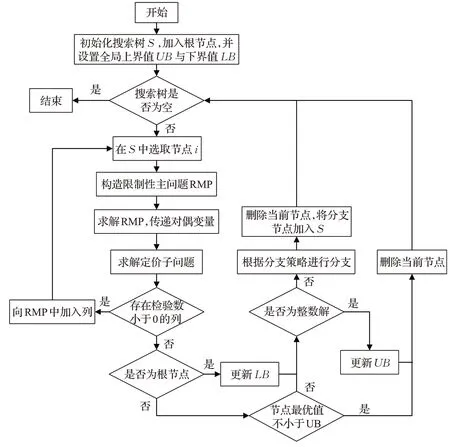
图1 算法流程图Fig.1 Algorithm flow chart

4.1 初始解生成策略

考虑到进出港时段交替，且船舶靠泊位置同之前进港船舶靠泊位置有关，因此本文针对每一艘船舶，根据进出港时段、有无偏好泊位，基于滞期成本与偏离成本之和最小的贪婪策略生成初始解。

步骤1若某船为乘潮船舶，比较预计到港时刻与潮汐时段，确定乘潮船预计最早进港时刻，且非乘潮船预计最早进港时刻为预计到港时刻。根据预计最早进港时刻从早到晚对船舶重新进行排序，从而得到初始船舶进港次序。

步骤2i表示进港次序的序号，t表示进出港时段，令i=1，t=1。

步骤3若t为进港时段，则转到步骤4，否则转到步骤5。

步骤4从序号i对应的船舶开始分配泊位：若某船没有偏好泊位且满足进港时间约束，则随机选择某位置为靠泊泊位；若此船有偏好靠泊位置、靠泊区间不与其他船重叠且满足进港时间约束，则靠泊泊位为偏好靠泊位置，否则为此艘船滞期成本与偏离成本之和最小时的岸线位置，若此时船舶进港完成时刻大于此时段结束时刻，则更新此船舶预计最早进港时刻，且重新生成包括此船在内的后续船舶的初始进港次序；若此时无满足靠泊约束的空闲泊位或该船不满足进港时间约束，则等到下一进港时段为此艘船舶分配靠泊位置。记录此时段分配泊位的最后一艘进港船舶的序号i′与已分配船舶实际开始进港时刻，令i=i′+1，并转到步骤6。

步骤5安排此时段内完成作业的船舶在满足时间约束条件下出港，记录船舶实际离港时刻，且其为此靠泊泊位的开始空闲时刻，并转到步骤6。

步骤6若i≤船舶总数，则令t=t+1，并转到步骤3，否则输出解。

4.2 分支策略

如果直接对主问题中的变量进行分支，那么需要在主问题中加入新的约束，从而生成新的对偶变量，这种分支策略会严重破坏子问题的结构，使得无论是主问题还是子问题，编程与计算都很繁琐。因此，本文对原问题变量进行分支，将约束条件加入子问题中。步骤如下所示：

步骤1针对子节点或者根节点计算得到的最优解，判断其是否为原问题的整数解，如果不是，则按照船舶编号从小到大的次序，找到第一艘含有非整数解的船舶i。

步骤2按照时刻t从小到大判断xit，选择第一个不是整数的xit。若不是整数，则对变量分支，包括t′≤t和t′＞t两支。主问题与子问题变换规则如下：对于t′≤t这一分支，将t′≤t加到子问题中，即令t′＞t的xit′都为0，且删除已加入主问题中含有t′＞t的的列。对于t′＞t这一分支，将t′＞t加入子问题中，即令t′≤t的xit′都为0，且删除已加入主问题中含有t′≤t的的列。

步骤3若所有xit为整数，则按照时刻t从小到大判断yit，选取第一个不为整数的yit。若不为整数，则分为t′≤t和t′＞t两支，且主问题与子问题变换参照步骤2。

步骤4若所有yit为整数，则按照位置j从小到大判断qij，选取第一个不为整数的qij。若=qij不为整数，则分为j′≤j和j′＞j两支，且主问题与子问题变换参照步骤2。

4.3 搜索策略

常见的搜索策略包括深度优先策略与广度优先策略，当搜索树的深度比较小时，采用深度优先搜索策略能较快找到问题的上界值。然而，本文的决策变量较多，将会产生比较多的分支，此时若采用深度优先策略需耗费很长时间才能找到最优解，因此本文采用广度优先策略，具体内容如下。

步骤1初始化搜索树，共有两个搜索树，分别为原搜索树与新搜索树。把根节点加入原搜索树中，计算根节点。

步骤2若根节点的解为整数解，则转到步骤7，否则转到步骤3。

步骤3把根节点的解作为全局下界值，并进行分支，在原搜索树中删除根节点，并把分支得到的子节点加入原搜索树。

步骤4若原搜索树为空，转到步骤7，否则，转到步骤5。

步骤5利用列生成算法计算原搜索树中的节点，若某节点最优值超过或者等于全局上界值，则剪枝，把此节点从原搜索树中移除，并转到步骤4，否则转到步骤6。

步骤6若节点最优值为整数解，则更新全局上界值，剪枝，并把此节点从原搜索树中移除，且转到步骤4，否则，进行分支，并把得到的子节点加入到新搜索树中，且转到步骤4。

步骤7若新搜索树为空，结束算法，否则，原搜索树等于新搜索树，并清空新搜索树，且转到步骤4。

4.4 列选取策略

在列生成过程中，当存在检验数小于0 的列时，把它加入到限制性主问题中，无法保证对应的决策变量的数值是1，即在最优解中没用到此列代表的船舶调度方案。因此，若每一次迭代只在限制性主问题中加入一条检验数小于0且绝对值最大的列，可能在迭代更多次数之后才能求得最优解，但这会降低每一次迭代问题的复杂度，减少求解时间。若把子问题中所有检验数为负的列都加入限制性主问题，将会降低整个列生成过程所需的迭代次数，但会增加限制性主问题的复杂度，使得限制性主问题的求解时间增加。因此，本文根据实验结果选择适合本问题的列选取策略。

5 算例分析

某集装箱码头拥有连续岸线1 000 m，由于船舶长度一般在50 的倍数附近，以50 m 为单位划分为一个距离单元，则可划分为20个单元，即岸线靠泊位置为1～20；计划期为12 h，以30 min 为单位划分为一个时间单元，则计划期可以划分为24 个单元，即进出港时刻为1～24时；根据港口实际作业情况，船舶安全航行距离为1 个时间单元，船舶从锚地航行到岸线的平均时间为1个时间单元，船舶进出港时段长度为4 个时间单元，且第一个时段为进港时段；第一个潮汐时段开始时刻为第9时间单元，结束时刻为第22时间单元，且潮汐时段间隔为36个时间单元。各船舶预计到港时刻与预计离港时刻随机生成，作业所需时间单元为[1，12]范围内的随机整数，有偏好泊位的船舶数量不超过船舶总数的2/3，且乘潮船舶数量不超过船舶总数的1/4。算法通过MATLAB R2014a和Gurobi求解器实现，并在3.60 GHz Intel Core i7-7700CPU和8 GB内存的计算机上运行程序。

5.1 确定列选取策略

根据上述数据，生成不同船舶规模情况下的实验，策略1 表示每次迭代在主问题中加入所有检验数为负的列，策略2表示每次迭代在主问题中加入一条检验数为负且绝对值最大的列，如表3所示。在所有实验中策略1 所需的计算时间小于策略2，且随着船舶规模的增加，二者计算时间之间的差距越来越大，因此本文采用策略1所代表的列选取策略，即在每次迭代时在主问题中加入所有检验数为负的列。

表3 列选取策略对比Table 3 Comparison of column selection strategy

5.2 方案有效性验证

若计划期内各艘船舶基本信息如表4 所示，其中3号船舶需要乘潮进出港口。结果如表5 与图2 所示，运行时间为162 s，目标成本为8 600元。在港口实际作业中，船舶按先到先服务（FCFS）策略进行调度，且保证滞期成本与泊位偏离成本之和最小，得到的调度方案如图3所示。

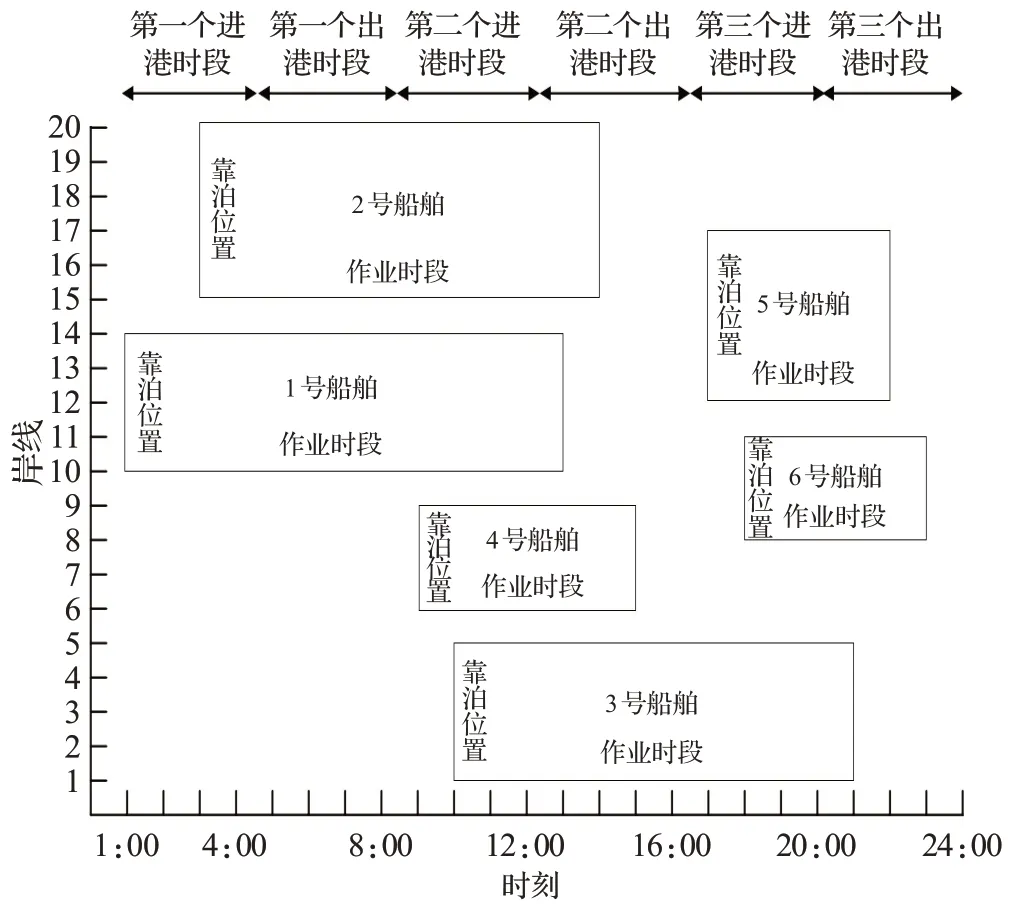
图2 最优集成调度方案Fig.2 Optimal integrated scheduling scheme

图3 FCFS调度方案Fig.3 Scheduling scheme of FCFS

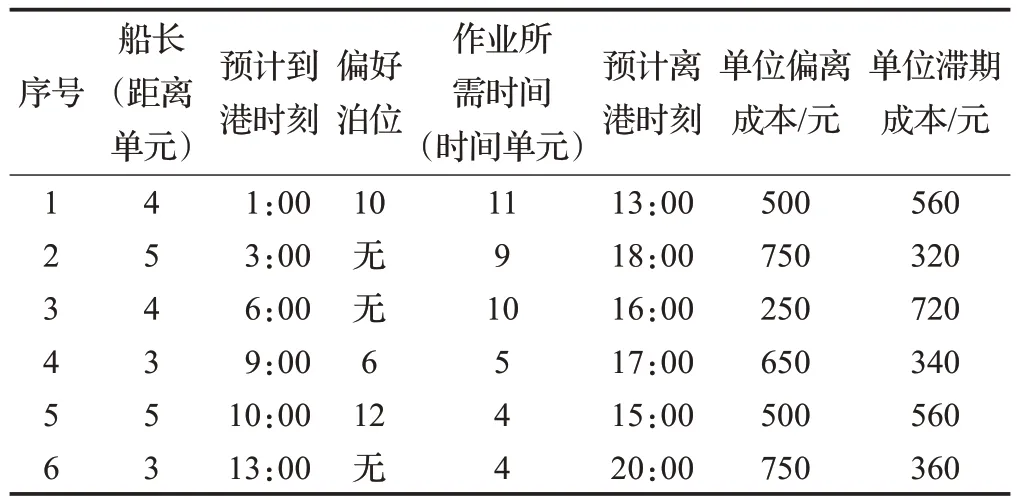
表4 船舶基本信息Table 4 Basic information of ships

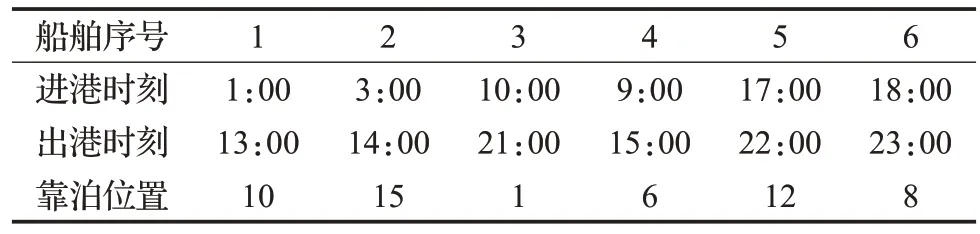
表5 船舶调度方案Tab.5 Ship scheduling scheme

在FCFS方案中，3号船舶先于4号船舶进港，此时4号船舶作业完成时刻为16，无法在此时段内完成出港过程，因此只能在下一出港时段出港，导致4号船舶滞期，并导致5 号船舶偏离偏好泊位。本文得到的协同优化方案改变了船舶进港次序，从而避免上述情况的发生。从结果来看，FCFS方案总成本为11 980元，集成调度方案总成本为8 600 元，则相比于FCFS 方案，集成调度方案降低了28.2%成本。

5.3 算法有效性验证

在不同船舶数量的情况下生成下列实验，针对同一种实验，在相同运行环境下，使用本文设计的分支定价算法、Gurobi 和传统遗传算法分别进行求解，比较三者的目标值与计算时间，并设定计算时间上限为3 600 s。若超过3 600 s，则算法终止，输出此时程序中的局部最优解，且用“—”表示无符合条件的解，GAP1表示分支定价算法与Gurobi目标值的差值，GAP2表示遗传算法与分支定价算法目标值的差值，如表6 所示。从中可知，分支定价算法与Gurobi 的目标值一样，验证了本文算法的准确性。同时，随着到港船舶数量的变大，Gurobi 求解所需时间呈现指数递增的趋势，当船舶规模不小于9 艘时，其在一个小时内已无法求出较优整数解，而分支定价算法对于不同船舶规模，都可在规定时间内求出最优解，且一般在25 min 以内。除此之外，GAP2 随着船舶数量的增加而变大，表明遗传算法求解质量越来越差，而本文设计的分支定价算法在所有算例中求得最优解。尽管遗传算法所需要的求解时间比较少，但分支定价算法所需时间也在可以接受的范围内，表明本文提出的分支定价算法求解效率较高。

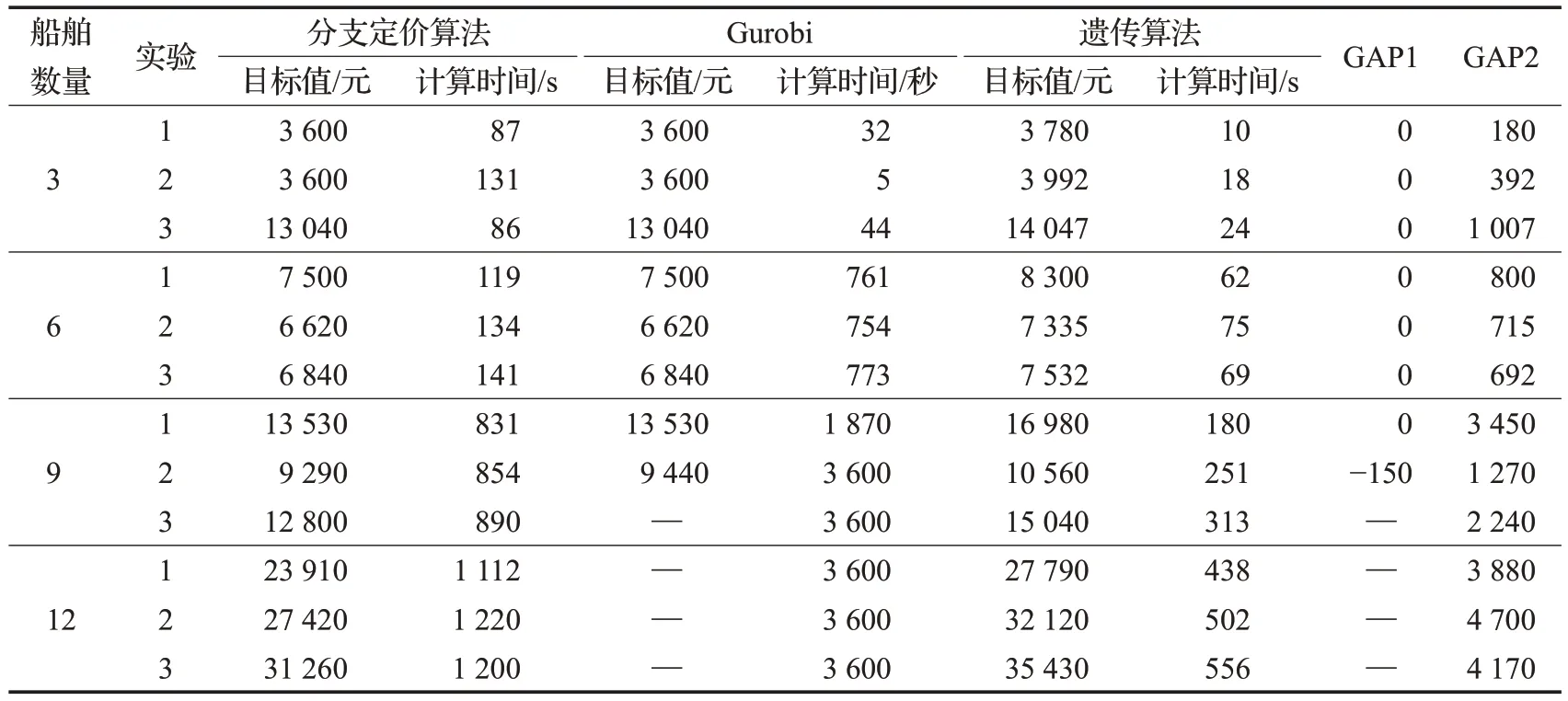
表6 算法结果比较Table 6 Comparison of algorithm results

5.4 进出港时段影响性分析

船舶进出港时刻由各进出港时段开始与结束时刻以及作业所需时间决定，它会直接影响本文模型的计算结果。由于每艘船作业所需时间是一定的，因此本文分析进出港时段长度对总成本的影响，如表7 所示。表7中的数据是改变船舶规模与进出港时段生成的，且为了保证实验的一致性，船舶数量多的实验的基本数据包括船舶数量小的实验的基本数据，例如船舶数量为8这一实验包括船舶数量为6 这一实验的6 艘船，并另外生成两艘船。在港口实际作业中，每艘船完成进出港过程所需时间最大约为40 min，为保证同一进出港时段中至少有1艘船舶能够安全通过航道，设定进出港时段长度分别为60、90、120、150、180，单位为min。

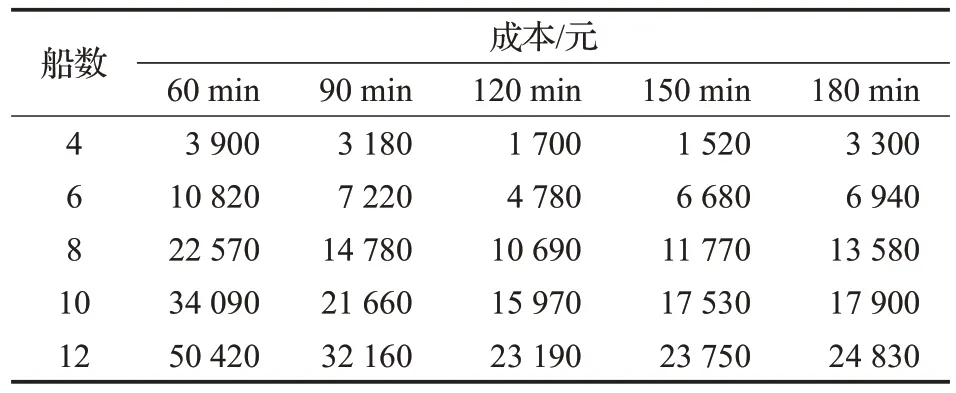
表7 进出港时段设置分析Tab.7 Inbound and outbound port period setting analysis

从表7 可知，随着船舶数量的增加，总成本逐渐增加，但对于同种船舶规模，总成本随着进出港时段长度的增加先变小再逐渐变大。当进出港时段长度增加，由于船舶需要在进港时段才能执行进港过程，在出港时段才能执行出港过程，导致部分船舶开始进出港时刻变大，从而造成滞期时间增加，进而引起总成本增加；当进出港时段长度增加到一定程度时，由于原本部分船舶到达港口的时刻在出港时段内或作业完成时刻在进港时段内，此时这些船舶可以在到达港口或作业完成时直接进出港口，导致船舶开始进出港时刻变小，从而降低滞期时间，进而引起总成本减小；当进出港时段长度继续增加时，船舶开始进出港时刻已经没有了减小的空间，此时船舶需要等待越来越长的时间才能开始进出港口，从而导致滞期时间的增加，进而引起总成本的增加。因此，港口需合理设置进出港时段，从而提高作业效率，降低成本。

6 结语

作为集装箱港口的重要资源，泊位有效分配与航道合理利用是港口管理水平和服务能力的重要体现。本文对连续泊位下的泊位分配与船舶调度集成优化问题进行了研究，在考虑了船舶动态到达、进出港时段交替、大船需乘潮进出港口与偏好泊位的基础上，以总成本最小为目标函数，通过建立模型与设计算法，给出了一个计划期内到港船舶泊位分配方案与进出港时刻，不仅可以降低总成本，还能减少船舶在港时间。

针对问题的特点设计了精确型分支定价算法，提出了有效的分支策略、搜索策略与列选取策略，可为解决类似问题提供了一种算法设计思路。

研究结果表明：在港口实际作业中，泊位分配与船舶调度之间的协同、乘潮船舶和进出港时段的长度是影响海侧运营效率的关键要素。其中，首先应重点关注泊位分配与船舶调度之间的交互影响；其次，在安排船舶进出港时需优先考虑乘潮船舶；最后，可依据每天船舶总量合理设置进出港时段。

在未来的研究中，可研究船舶调度、泊位分配与岸桥调度集成优化问题，并改进子问题的求解方法，降低计算时间。