静息态下基于变分模态分解的生命体征检测

安美晨，王 鹏，蔡 超，彭 凯

华中科技大学 电子信息与通信学院，武汉430074

人体各项生理指标的实时变化能够在一定程度上作为某些特定疾病的检测手段，同时也能反映出检测目标的身体状况，因此对人体的生命体征进行实时监测在现代医疗系统中起着至关重要的作用[1-3]。传统的医疗检测系统主要使用接触式设备[4]，如贴片式心率仪、指夹式血压计等，需要用户一直佩戴设备才能实时获取体征信息；由于器材均为有线设备，用户在佩戴设备过程中的活动范围也受到限制；在对不同病患进行检测前也需要对设备进行消毒处理。诸如此类的问题使得接触式检测设备在实际使用的过程中存在着诸多不便。

近年来，随着4G、5G的不断发展，无线通信效率得到飞速提高，非接触式生命体征监测技术也得到了发展。目前主流的无线的技术有WiFi、UWB、FMCW 雷达。（1）文献[5]中的作者建议使用WiFi的RSS进行呼吸监测。但是，这要求人员手持设备或站在TX 和RX 节点之间的视线路径中以进行精确监控，通过接收信号的强度差异确定目标距离变化，进而确定人体呼吸频率。由于室内条件下WiFi 信号存在多径效应、信号的强度会产生波动，因此其稳定性和准确性会受到影响[5-8]。（2）基于UWB 雷达信号的无线监测技术主要利用窄带脉冲雷达回射信号的相位变动来进行生命体征监测[9]，由于信号相位相较于信号强度更为敏感，因此更易获取生命体征；但是在距离较远情况下，微小的环境噪声会影响信号检测的准确率。（3）基于毫米波FMCW雷达信号的无线监测技术使用连续调频波信号[10-11]，通过发射及接收信号的频率差异确定目标距离，具有较高的灵敏度，同时可以通过分离不同的频率成分来区分不同目标，藉此去除目标间干扰，稳定性较强。

在进行非接触式生命体征监测时，为了获得较好的观测效果，需要对呼吸信号及心跳信号进行分离提取。常用的信号分离方法有带通滤波器、经验模态分解（EMD）等。传统的带通滤波器能够有效分离频率差异较大的混合信号，但是由于呼吸信号与心跳信号的频率范围较为接近，分离出的信号中往往包含有另一信号的谐波分量，并不能够满足医学监测的高精度需求；EMD通过对数据进行平稳化分解，将信号按照不同频率范围进行分离，能够处理多数信号。但是在使用EMD 算法进行分离时无法手动确定不同模态的频率范围，分离结果需要进行二次判断确定心跳和呼吸信号。为了解决这一问题，本文提出了VMD算法，能够较为有效地完成呼吸信号和心跳信号的分离工作，从而提高监测效果。

1 生命体征检测模型

本章中，介绍FMCW雷达系统的调制原理。FMCW雷达系统包括射频（RF），例如发射（TX）和接收（RX），模拟时钟，以及数字电路，例如模数转换器（ADC）、微控制器（MCU）和数字信号处理器（DSP）。图1 显示了典型FMCW雷达系统的简化框图。FMCW雷达发送合成器生成线性FMCW信号，通过TX天线发送。雷达信号遇到物体时将被反射，经过RX接收。然后，采用同相和正交采样，正交接收器负责捕获回波信号并将其与发射信号正交混合。低通滤波器用于滤除高频部分并获得中频（IF）信号。最后，中频（IF）信号由ADC 采样，存储到寄存器中。

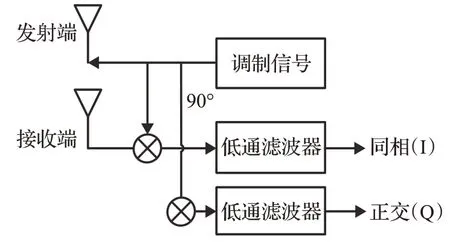
图1 FMCW 雷达调制系统Fig.1 FMCW radar modulation system

1.1 FMCW雷达

FMCW 雷达发送的信号为线性调频脉冲信号，通常也被称为Chirp信号，FMCW雷达具有更高的距离和速度分辨率，并且能够区分多个目标并提取目标速度信息，图2（a）为其在时间域上的表现形式，图2（b）为该信号在频域上的表现形式。

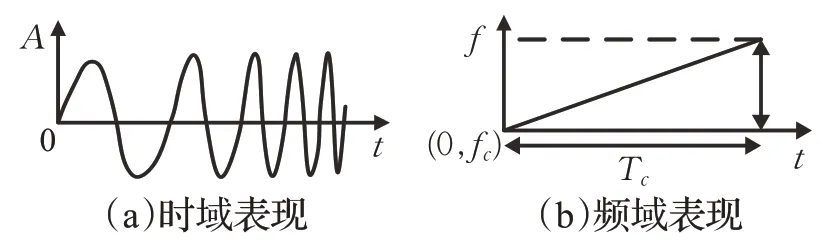
图2 线性调频脉冲信号Fig.2 Chirp signal

FMCW雷达系统发送的线性调频脉冲信号表示为：

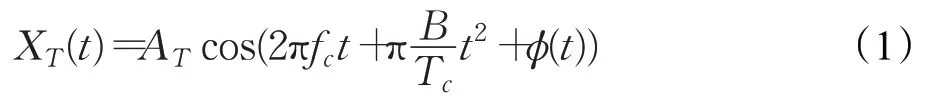
其中，fc是线性调频信号的起始频率，B是带宽，AT是发送信号的幅度，ϕ(t)是相位噪声，Tc是线性调频信号脉冲的宽度，而B/Tc是线性调频信号的斜率，代表频率的变化率。

1.2 FMCW雷达检测生命体征原理

微小的振动会影响信号，具体反映在信号相位上的变化，利用该原理可以检测人体胸腔移动，从而检测生命体征信息。假设在距离R处有一个物体，那么经过该物体反射接收到的信号：

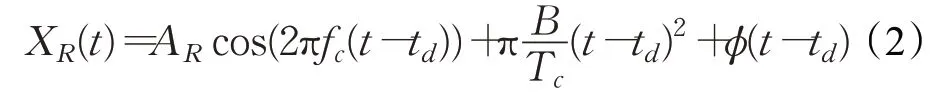
其中，td=2R/c，接收信号和发送信号由两个正交的I/Q通道混合，然后通过低通滤波器滤除高频信号，以获得中频信号：

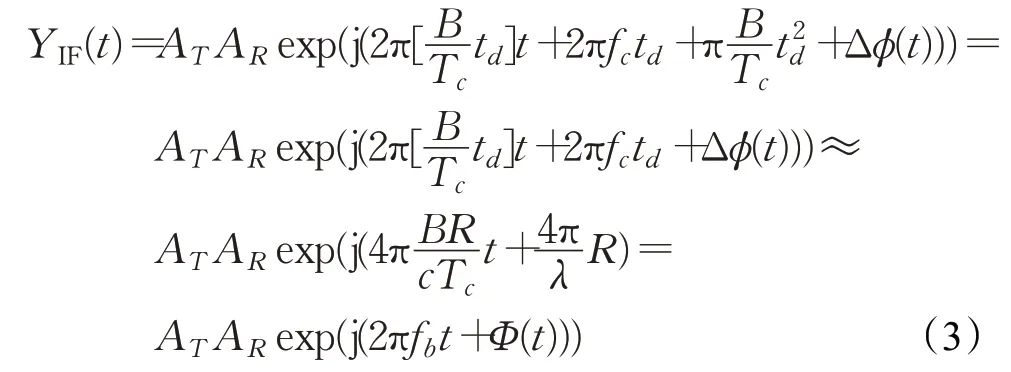
其中，fb=2BRt/(cTc)，Φ(t)=4πR/λ。在等式（3）中，在实际情况中非常小（大约10-6阶），可以近似忽略。根据文献[12]中距离相关效应，剩下的相位噪声也可以忽略不计。得到的中频IF信号如图3所示，对于固定距离为R的物体，理想情况下其反射到的信号是一个频率为fb的正弦波。

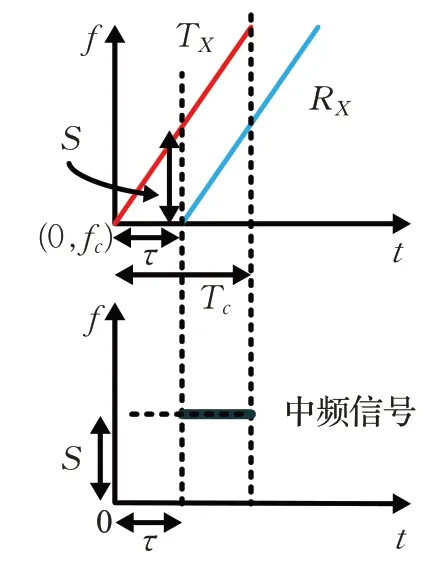
图3 生成中频信号Fig.3 Generate IF signal

人体心脏跳动和呼吸会导致胸腔的移动，如表1。正常一个成年人的呼吸引起的胸腔起伏位移能达到1～12 mm，心跳引起的位移是0.1～0.5 mm。

表1 正常人生命体征参数Table 1 Normal person’s vital signs parameters

根据式（2），假定距离X处物体是一个成年人，那么实际上R=X+d(t)，d(t)是胸腔随时间发生的位移，那么式（3）可以改写成：

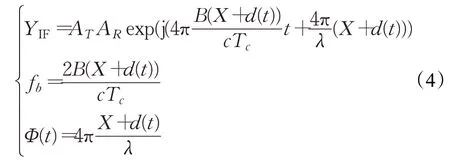
对于fb，由于d(t)是毫米级的移动，而毫米波雷达的距离分辨率是厘米级的，因此忽略d(t)的变化不影响fb。为了测量胸腔小规模的振动d(t)，可以观察到，在固定距离X处的相位Φ(t)相对于λ随d(t)变化，则连续两次之间的相位变化ΔΦ=4πΔd/λ。由于毫米波波长短，以λ=4 mm 为例，当位移变化Δd=1 mm 时，相应的相位变化可以到π。

2 呼吸和心跳信号分离

对于心率的检测，相比呼吸，心跳导致的胸部位移更加微小，很难进行检测或者误检。接收到的信号主要包含四个分量：

目标的呼吸。成年人的呼吸频率范围从0.16 Hz到0.6 Hz。

目标的心跳。成年人的心跳频率范围为0.8 Hz至2 Hz。

环境中的噪声。由所处环境中带来噪声振动的干扰，其频率范围在0.5 Hz至10 Hz。

人体动作的影响。诸如手臂摆动，脚抖动类的人体运动，可能会带来0.5 Hz至2 Hz的频率干扰。

可以看到，接收信号的四个分量在频率上重叠，因此，具有指定频率范围的简单带通滤波器无法滤除由振动引起的不希望的噪声。

2.1 传统分解方法

为了将生命体征信号与其他干扰区分开，一些文献[13-15]中尝试直接利用频率分析和带通滤波器（BPF）估算心率，这样的确可以在理想的条件下取得很好的效果。然而，由于呼吸的谐波影响[16]，心跳的速率很容易使用错误的峰进行估算。因此，为避免这种影响，获得更高的估计精度，本文提出了使用模态分解算法将目标的呼吸信号和心跳信号与噪声分离开，除呼吸信号的谐波影响，并进一步估算了心率，提高心跳信号的信噪比（SNR），进而提高估计精度。

2.2 变分模态分解

变分模态分解（VMD）是一种基于维纳滤波和希尔伯特变换的新的自适应分解方法[17]。通过搜索约束变分模型的最优解，可以将原始信号分解为一组具有稀疏特征的VIMF分量。每种模式在中心脉动ωk周围都是紧凑的，并且其带宽是使用移位信号的H1 高斯平滑度估算的。VMD被写为一个约束变分问题[17]：

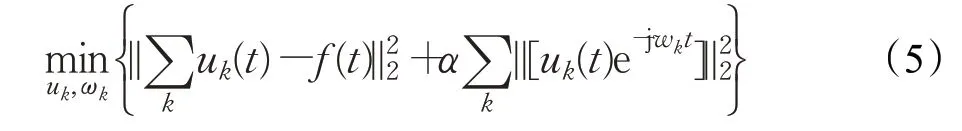
其中，k是VIMF 分量的个数，f是输入信号，并且f=s(n)；此外，{uk}={u1,u2,…,uK}和{ωk}={ω1,ω1,…,ωk}分别是所有模式及其中心频率的简写。可以通过引入二次罚函数和拉格朗日乘数来解决等式（5）。应用微分的欧拉-拉格朗日公式如下[17-18]：

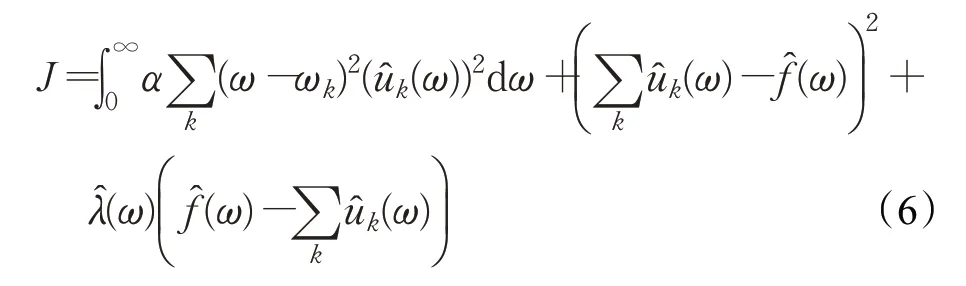
其中，α表示数据保真约束的平衡参数。然后，用交替方向乘子法（ADMM）求解方程式计算这些中心频率和模式函数。从频谱域的解中获得的所有模态分量：

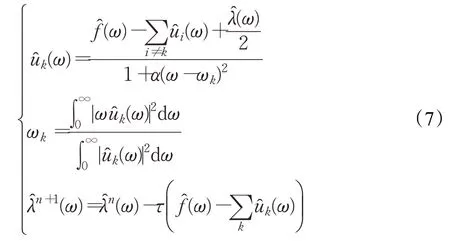
其中，ωk是在相应模式的功率谱的重心处计算得到，使用梯度下降更新。

为了避免跟各分量端点处出现重叠现象的端点效应，在本文中采用的方法是对称拼接的方法，把原信号复制一份然后拼成两半，一半对称放前面，一半对称放后面，组成一个镜像的信号进行处理，最后的输出再从中提取原始长度的信号。

3 实验结果与分析

3.1 实验环境介绍

本文使用的是德州仪器（TI）的毫米波雷达IWR1443实现，它是集成的单芯片FMCW 雷达传感器，工作在77～81 GHz 频段，实验的参数配置如表2。实验应用场景如图4所示。被测人员坐在雷达前并保持静止，佩戴接触式设备小米智能手环Mi3[19]，用于捕获心跳速率，文献[19]中使用小米手环和三导心电图机对比，验证了在静息状态下小米手环测量心率的可靠性，具有一定的心率参考价值。IWR1443集成了TI的高性能C674x DSP子系统，用于雷达信号处理，可以在雷达板上进行编程。但是，为了观察实验结果和数据分析，希望获得原始数据用于算法验证。因此，DCA1000 在流数据模式下结合IWR1443来收集雷达的原始数据。

表2 IWR1443参数设置表Table 2 IWR1443 parameter setting

图4 实验设备安装Fig.4 Experimental equipment installation

3.2 目标信息提取

根据流程构造的距离时间-热图显示在图5 中。图5显示了每分钟1 200帧内距离变化的信息，可以看到在1.3 m 范围内有来自不同目标的反射。在实验过程中，人体始终坐在雷达的前面（参见图4），这意味着目标位置仅由于心跳和呼吸运动而上下移动。

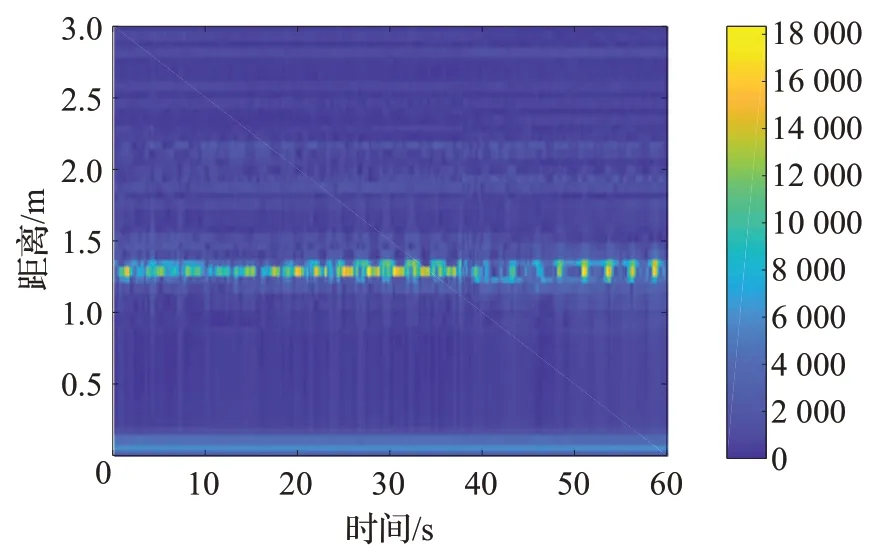
图5 距离FFTFig.5 Range FFT

如前所述，运动目标总是带来更强的信号功率，这反映在图像的较亮部分。在选取目标距离单元进行相位提取，对相位进行DC去除和差分运算，得到目标相位提取结果如图6（a）所示，然后对相位展开行执行第二次傅里叶变换，以获得相位信号的频谱，如图6（b）所示，可以看到在图中0.2 Hz、0.72 Hz 和1.441 Hz 处有明显峰值，对应与呼吸频率、谐波频率以及心跳频率。

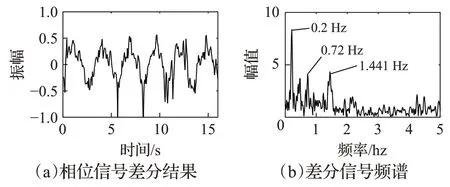
图6 相位信号Fig.6 Phase signal

3.3 模态分解

对于图6（a）的相位信号使用经验模态分解（EMD）算法，可以将信号分解为若干个IMF分量{imfK}={imf1,imf2,…,imfk}，如图7 左列，得到了7 个分量，对每个分量进行傅里叶变化，得到其对应的频谱图，如图7 右列，可以看到imf2、imf3 和imf5 对应的分量频率为1.42 Hz、0.76 Hz和0.21 Hz。

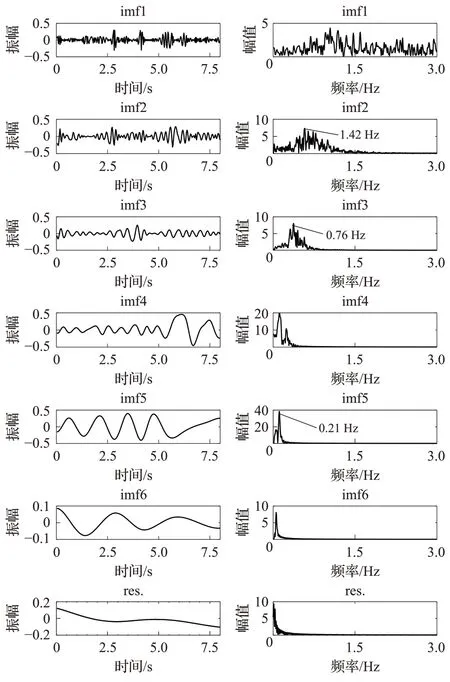
图7 EMD分量及频谱Fig.7 EMD components and spectrum

在预处理之后将VMD 算法应用于接收到的数据，可以将信号分解为多个VIMF，{uk}={u1,u2,…,uK}。根据呼吸和心跳的频率范围，可以选择代表呼吸和心跳的ur和uh分量。在本文中，设定k=3,α=2 000,τ=0,ε=10-7，根据以往的经验信号的呼吸和心跳分量分别固定是VIMF1和VIMF2，如图8。

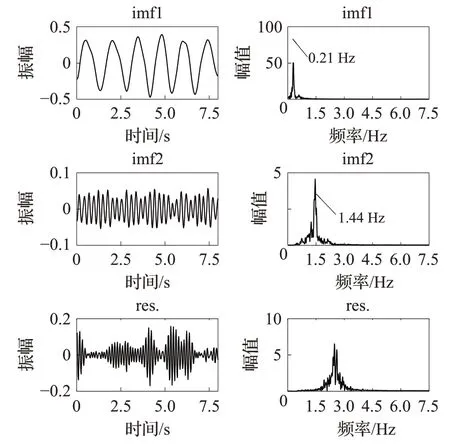
图8 VMD分量及频谱Fig.8 VMD components and spectrum

为了有效地实现心跳和呼吸信号的分离，本文提出使用模态分解的办法，很明显，图8 相比图7 中的信号，VMD 更容易得到心跳的真实信号，消除了呼吸带来的干扰。对比而言，EMD 其分离的IMF 分量个数不能人为设定，需要一直循环迭代直至条件不满足，而由于这种分量个数不确定的原因，对于分解后的处理是十分不便的，如果不观察分解的结果，无法确定表示呼吸和心跳分量的对应关系，而VMD 则可以；当VMD 分量个数设置K=3 时，其呼吸和心跳分量固定为VIMF1 和VIMF2，同时EMD 分解的结果仍然存在呼吸二次谐波的分量，为了防止拾取错误的峰值估计心率，需要再分解后进行额外的处理。另一方面，使用VMD 所提出的方法获得的心跳波形具有正弦趋势，更明显的是，图8中的频域具有高分辨率。

3.4 对比分析

信噪比标准取决于所需的性能和检测精度系统，因此需要参考生命体征信号来确定不稳定的SNR 标准。为了进行定性分析，在频域中重新定义了生命体征信号的SNR。如果将呼吸速率估计为频谱中峰值的频率f0，则SNR的计算如下：

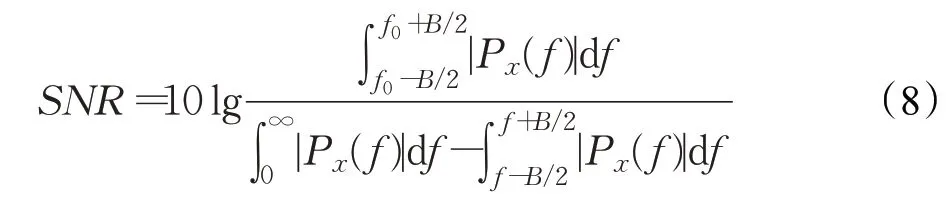
其中B是由FFT点的数量和要求的采样频率确定。

对10 名测试人员进行实验测试，采集到的数据信息使用Matlab分别使用模态分解EMD、VMD算法以及FastICA 算法处理，并统计运行时间；独立成分分析（ICA）是常用的盲源分离信号处理方法，应用非常广泛，在已知源信号数目时，可以实现对混合信号的盲源分离，结果如表3所示。

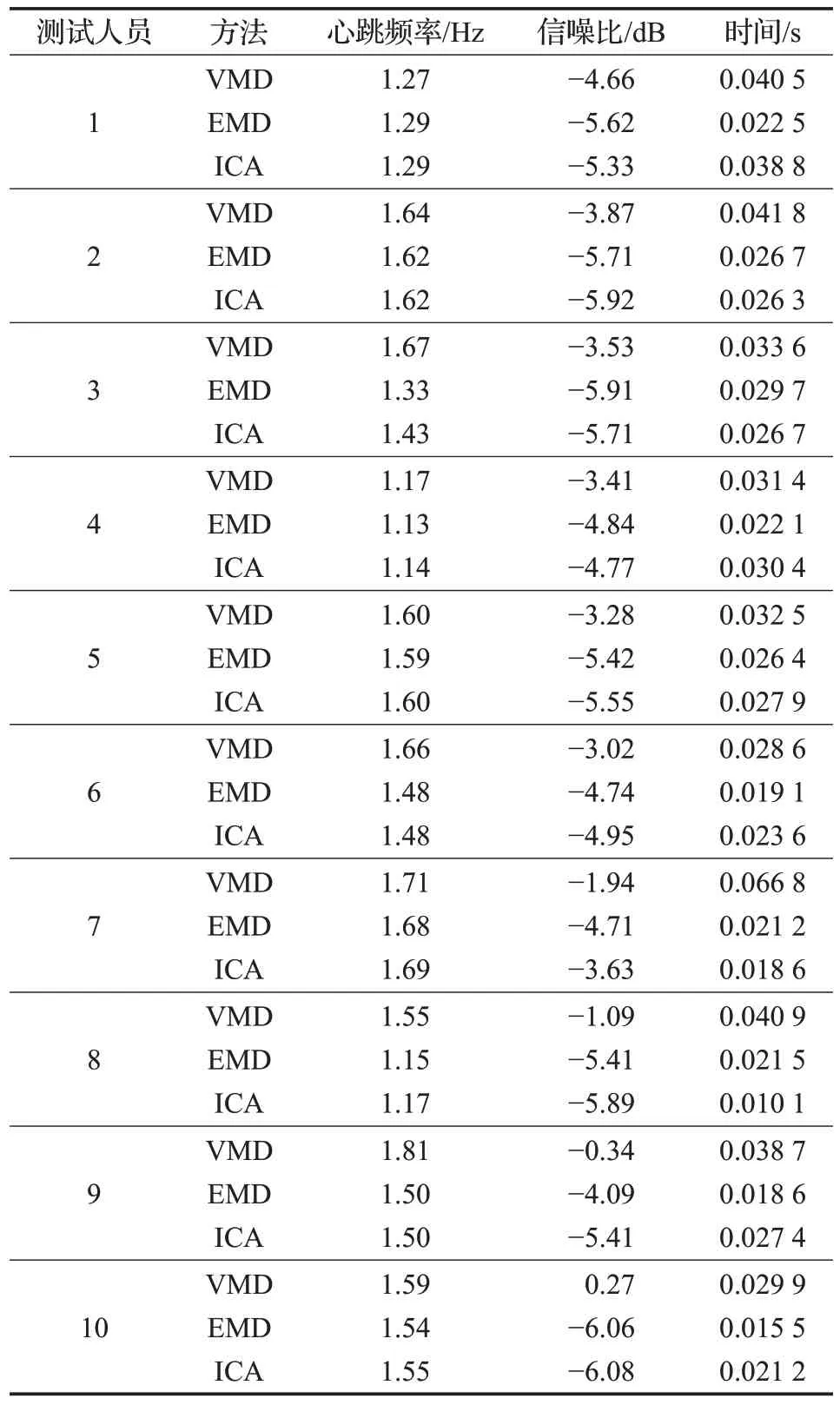
表3 提出的方法与其他方法提取心跳信号的结果对比Table 3 Comparison of heartbeat signal extraction results between proposed method and other methods

通过本文所述方法，VMD 分离的信号平均SNR 相比EMD改善为2.766 2 dB，相比ICA改善为2.312 0 dB，具有较高的信噪比，VMD需要的计算时间长，但是其中未统计EMD 后续额外操作的计算时间，例如根据相关系数选取其中IMF 分量重构心跳信号；较高的信噪比（SNR）对于帮助降低误报概率的雷达系统至关重要。这对于医疗监控应用尤其重要。此外，高SNR 可以有助于在更复杂的环境中提高检测精度，并增加检测范围，这可以帮助雷达适应许多不同的环境，甚至适应不同的人体姿势。

如图9所示，将模态分解算法处理得到的心率结果与参考心率进行比较，使用VMD 算法估计心率误差95%在2.47 BPM（beats per minute，BPM）范围之内，使用EMD 算法估计心率误差95%在3.22 BPM 范围之内。结果表明，在相同的测试环境下，VMD的结果要优于EMD，提高了系统检测的准确度。

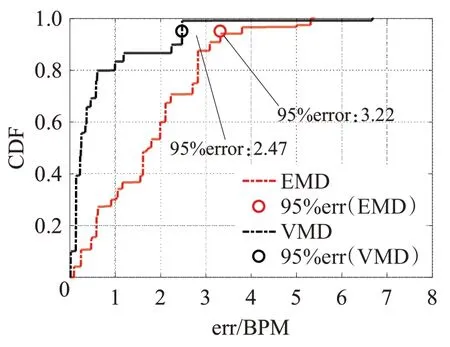
图9 EMD和VMD检测误差CDFFig.9 EMD and VMD detection error CDF

4 结论

本文基于毫米波FMCW 雷达实现生命体征监测，提出了基于变分模态（VMD）分解的算法提取目标的呼吸和心跳信号。实验数据结果表明，基于VMD 的生命体征信息提取方法能够准确地分解呼吸和心跳信号，得到目标呼吸和心跳频率，相比传统滤波器、经典的经验模态分解（EMD）方法和主成分分析（ICA）算法，分解得到的信号更好地避免了呼吸引入的二次谐波影响，得到的信号具有较高的信噪比，得到的结果具有更小的误差，对系统有更好的改进，极大地提高系统的稳定性和检测精度。