基于卷积长短时记忆网络的CPI预测

陈逸东，陆忠华

1.中国科学院 计算机网络信息中心 高性能计算部，北京100190

2.中国科学院大学，北京100049

居民消费价格指数（CPI）反映一定时期内人们购买一组代表性商品和劳务总花费的变化情况，是国民经济核算统计的核心指标之一。如果用CPI 来衡量价格水平，则通货膨胀率就是不同时期的CPI 变动的百分比。按照国际惯例，当CPI增幅连续超过3%时，即意味着发生了通货膨胀；当CPI 低于1%时，则有通货紧缩的风险。当通货膨胀发生时，货币贬值，大多数居民的利益和生活会受到影响。CPI关系国计民生，是管理层制定宏观经济政策、分析货币市场和债券市场及央行公开市场操作的重要参考依据。从我国货币政策目标来看，我国的货币政策目标是“保持物价稳定，并以此促进经济增长”，物价稳定是我国宏观经济决策的重要目标之一。如何科学预测我国CPI，并在此基础上运用一定的技术手段，实施超前性的货币政策，对于全面把握经济发展趋势、经济安全以及社会稳定具有重要的意义。

目前，国内外对于CPI研究主要是利用历史月度数据构建模型。Kontonikas 等[1]基于GARCH 模型分析了英国月度的宏观经济数据，将英国1972 年到2002 年的通胀分解为短期通胀与长期通胀，提出根据通货膨胀预测值的变化制定宏观经济政策，以引导通货膨胀预期向预定水平靠拢。Jonathan等[2]采用贝叶斯平均模型预测对美国四个不同时期的通胀进行预测，将预测结果与等权平均模型预测的结果进行比较，论证了贝叶斯平均模型在预测美国通胀方面通常比简单的等加权平均模型表现得更好。Carstensen 等[3]建立随机平均波动率模型对美国短期通胀进行预测并与ARMA模型进行对比分析。分析结果表明随机平均波动率模型相较于ARMA时间序列模型在预测美国通胀上有更高的精度和更好的鲁棒性。Koop等[4]基于广义的菲利普斯曲线（Phillips curve），采用动态的计量模型预测美国每个季度的通胀变化率。结果表明动态计量模型对于通胀的预测精度相较于静态计量模型有极大的改善。Ahmar 等[5]使用ARIMA 模型对印尼CPI 进行预测，发现最优模型为ARIMA（1，0，0）。赵影等[6]分析了影响CPI的驱动因素GDP 和M1，采用二元回归模型对我国未来CPI 走势进行预测。雷鹏飞等[7]和肖良等[8]根据CPI 序列的季节性特点，基于季节性ARIMA 模型对我国CPI 波动进行预测。CPI 的主要预测方法还包括ARX 神经网络[9]、RBF神经网络[10]和支持向量回归[11]等。

然而，这些基于月度数据的预测方法很难充分利用当月可观测到的信息。举例说明，假如要预测2020年6月的CPI，可在6 月9 日（国家统计局发布上月CPI 的日期）获得5 月CPI 数据后用月度数据建模。这样建立的模型忽略了6月9日至6月30日这段时间内可观测到的一些金融市场变量对CPI的影响，这些金融变量包括了农产品的价格波动、大宗商品的价格波动和外汇市场的汇率波动等。按照国家统计局2020 年公布的指数构成，我国的CPI 包括食品、烟酒及用品、衣着、家庭设备用品及服务、医疗保健及个人用品、交通和通信、娱乐教育文化用品及服务、居住等八大类262个基本分类。截至2020 年12 月1 日，我国上市的期货交易品种有上海交易所的铜、铝、天然橡胶和大连交易所的玉米、黄大豆1 号、黄大豆2 号、郑州交易所的菜籽油、强麦、普通小麦、棉花、白砂糖等共60个品种。能否发掘这些变量中的日度信息，为CPI 提供更精确的预测，本文将对这一问题展开研究。

期货作为现货的一种远期交易，其对现货价格的引导作用已经被国内外学者多次证实。国内外学者从期货价格与宏观经济变量相关性的角度出发，研究了商品期货的价格发现功能[12-14]。Bigman等[15-16]提出利用期货对现货价格的引导作用来预测CPI 的变化。Foster[17]检验了美国原油期货的价格发现功能，结果表明期货市场对于宏观经济的早期风险发现具有预警作用，一般情况下期货市场的走势领先于宏观经济指标3到6个月。周舟[18]采用计量分析方法对我国商品期货价格指数与CPI的关系进行了实证分析，检验结果显示，中国商品期货价格指数先行消费价格指数5个月。王楠[19]基于向量自回归（VAR）模型研究郑商所农产品期货价格的基准价格指数序列ESABI和CPI的关系，揭示郑商所农产品期货对通货膨胀的预警作用。随着我国期货市场的发展与壮大，期货品种更加丰富多样，商品期货的整体波动更能反映实物未来一段时间的变化趋势。

在上述研究工作的基础上，本文考虑利用期货市场的日度交易数据发掘我国期货农产品价格对于CPI 的先导作用。期货数据种类繁多，卷积神经网络（CNN）具有特征提取和特征识别的能力，被广泛应用于空间特征提取。长短期记忆网络（LSTM）已成功应用于时序依存性数据建模[20]，本文将CNN和LSTM网络联合用于期货面板数据的特征提取和CPI 预测。CNN-LSTM 深度网络模型最早由Deng等[21]提出和运用。Bae等[22]和Tara等[23]将CNN-LSTM 深度网络用于视频分类，采用卷积神经网络提取视频的空间特征，采用长短期记忆网络从连续的音频信息中提取数据的序列特征，该模型将二者提取到的特征视为一个新的特征作为全连接层的输入，将不同视频的分类结果作为全连接层的输出。然而，该模型是对三个独立的网络分别进行训练，再通过组合层对三个输出进行组合。谷歌Tara 等在上述模型的基础上提出了CNN-LSTM-DNN 深度网络模型[23]，将CNN、LSTM和DNN合并为一个统一的框架共同训练。该模型成功运用于语音识别，极大降低了语言识别的词错误率（word error rate）。

期货面版数据既具有类似图像的空间特征，又具有时域相依特征，为此本文提出采用卷积神经网络对期货面板数据进行空间特征提取，将提取到的特征作为LSTM 网络的输入，最后用全连接层输出CPI 的预测结果。本文的实验数据采用国内市场的三大种类期货合约：农产品期货、金属期货和能源期货的日交易数据。通过训练CNN-LSTM 深度网络模型，学习空间特征之间的时间关联，动态定量预测未来一段时间内CPI的变化，为CPI和其他宏观经济指标的预测提供一种参考。

1 基于CNN-LSTM的CPI预测模型

1.1 模型建立

CPI 数据是宏观经济数据，以月为单位发布，数据本身所包含的信息有限。研究表明商品期货的价格波动与CPI 波动之间存在密切的关系。商品期货包括农产品期货、能源期货和有色金属期货。本文首先将每日商品期货的交易信息转换为类图像，以农产品期货为例，农产品期货合约包括苹果、小麦和大豆等不同种类商品，每一种农场品期货合约又包括了近期合约、次近期合约和远期合约。本文将每一类数据视为一个特征，由于每个特征包含不同交割月的数据，将所有数据按列拼接成二维面板数据（如图1所示），该面板数据包含空间特征和时间特征，采用卷积神经网络对面版数据进行特征提取，采用LSTM网络输出CPI的预测值。

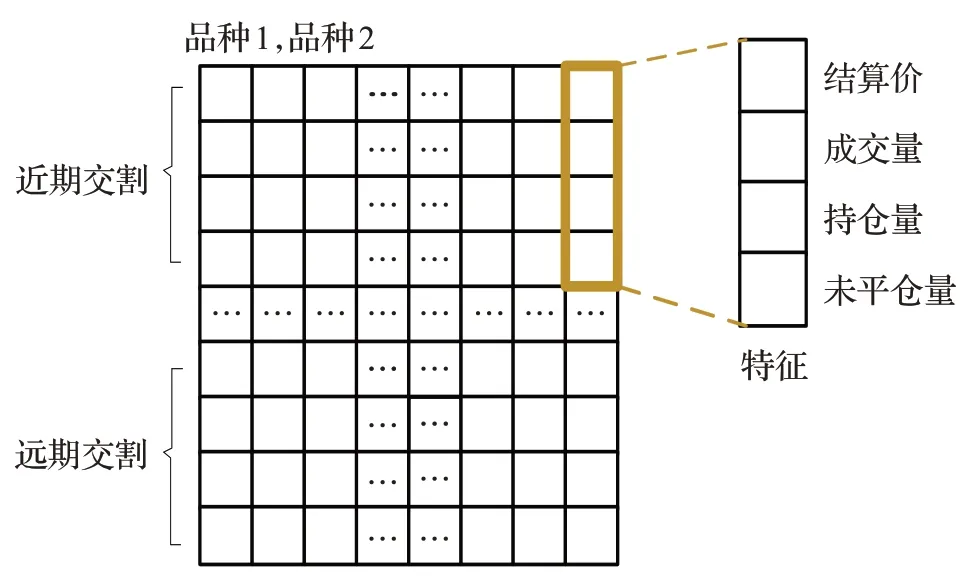
图1 期货面板数据结构Fig.1 Futures panel data structure

1.1.1 基于CNN的期货特征提取

CNN可以用于研究任何输入和输出之间的映射关系而不需要建立精确的数学表达式。本文所使用的卷积神经网络主要包括卷积层与池化层，通过提取面板数据具有代表性的全局特征，建立输入与输出之间的映射关系。基于CNN 的期货特征提取基本过程如图2 所示。卷积层对每个时刻输入的面板数据采用多个卷积核对面板数据进行扫描，通过卷积运算提取特征，将提取到的特征进行池化运算（Pooling）。实现池化最常见的方法是对每个过滤器的结果应用max 操作。这里使用最大池化有两个原因。第一，通过消除非最大值减少了上层的计算量。第二，提取不同区域的局部依赖关系，保留最显著的信息，将获得的区域向量作为LSTM网络的输入。

1.1.2 基于CNN-LSTM的CPI预测

提取特征以后，针对CPI 数据具有时间相依的特点，长短期记忆网络（LSTM）来输出CPI的预测值。

长短记忆网络在隐含层引入了内存单元来代替传统的人工神经元。有了这些记忆单元，网络能够有效地将记忆关联起来，并进行远程的时间输入，适合动态掌握期货合约的数据结构，具有较高的预测能力。CNNLSTM深度网络通过最小化CPI的预测值与实际值之间的均方误差进行训练。对于测试集上的面版数和CPI数据损失函数定义为：

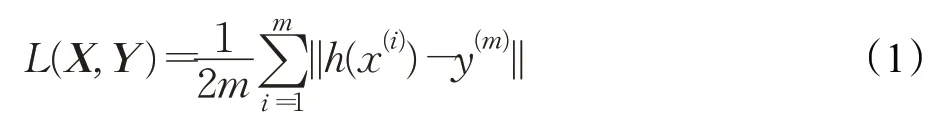
其中，X={x(1),x(2),…,x(m)}分别表示m个时刻的面板数据，h(x(i))表示每一个时刻CPI的预测值，Y={y(1),y(2),…,y(m)}表示每一个时刻CPI 的实际值。深度神经网络存在两种可能影响模型训练效果的问题，一是梯度消失导致神经网络难以收敛，二是过拟合导致测试集失效。Batch-Normalization（BN）能有效解决梯度消失问题，Dropout技术通过阻止神经元共适应能够缓解过拟合问题。本文在设计CNN-LSTM 深度网络时添加了BN 层和Dropout层以优化网络结构。

1.2 模型训练

模型在训练过程中分为两个阶段，第一个阶段是网络预训练，第二个阶段是网络动态训练和预测（参见图3）。在网络预训练阶段，模型采用t0时刻之前的数据集训练深度网络。当训练完成以后，进入动态训练和预测阶段。在这个阶段，对于每一个tn时刻的数据，模型采用tn时刻之前包括tn时刻的数据作为训练集训练网络，预测(tn,tn+Tn)时间段内的CPI 值。预测完成之后，滑动时间窗口，采用tn+1=tn+Tn时刻之前的数据训练网络。重复上述过程，不断滑动时间窗口，直至tN时刻（tN表示滑动窗口的终止时刻），所有数据预测完成。

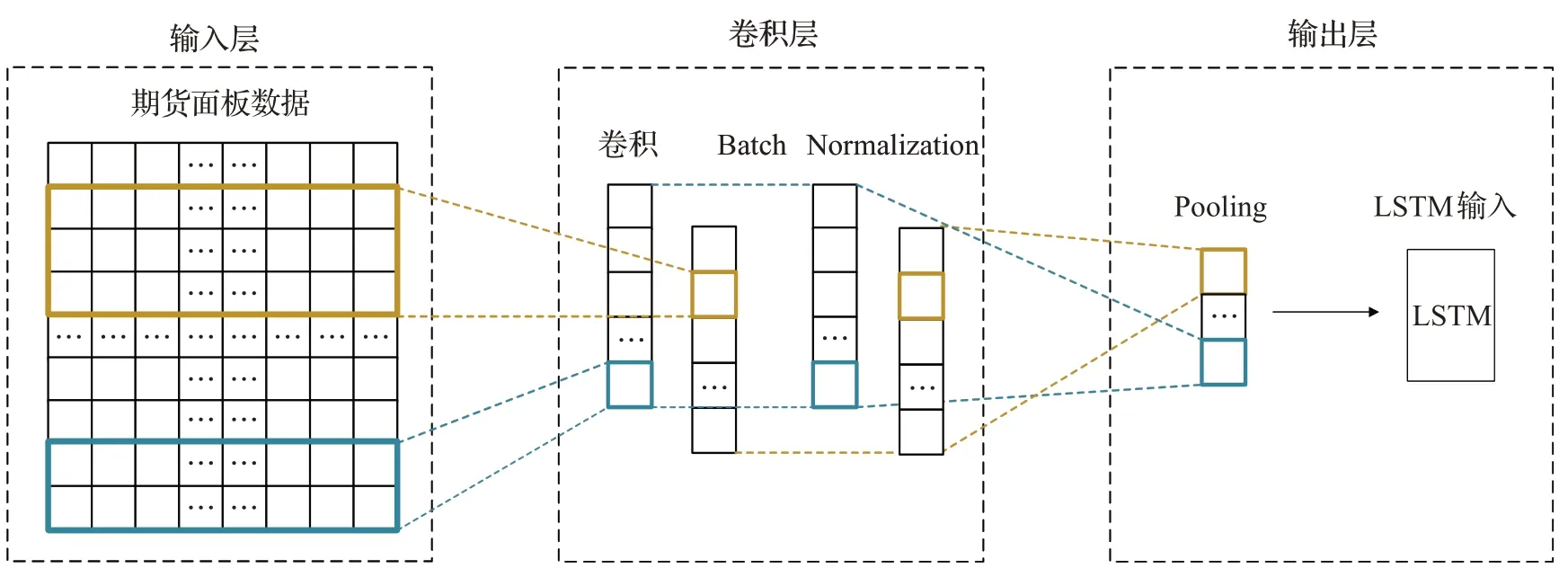
Fig.2 Feature extraction based on CNN图2 基于CNN的期货特征提取

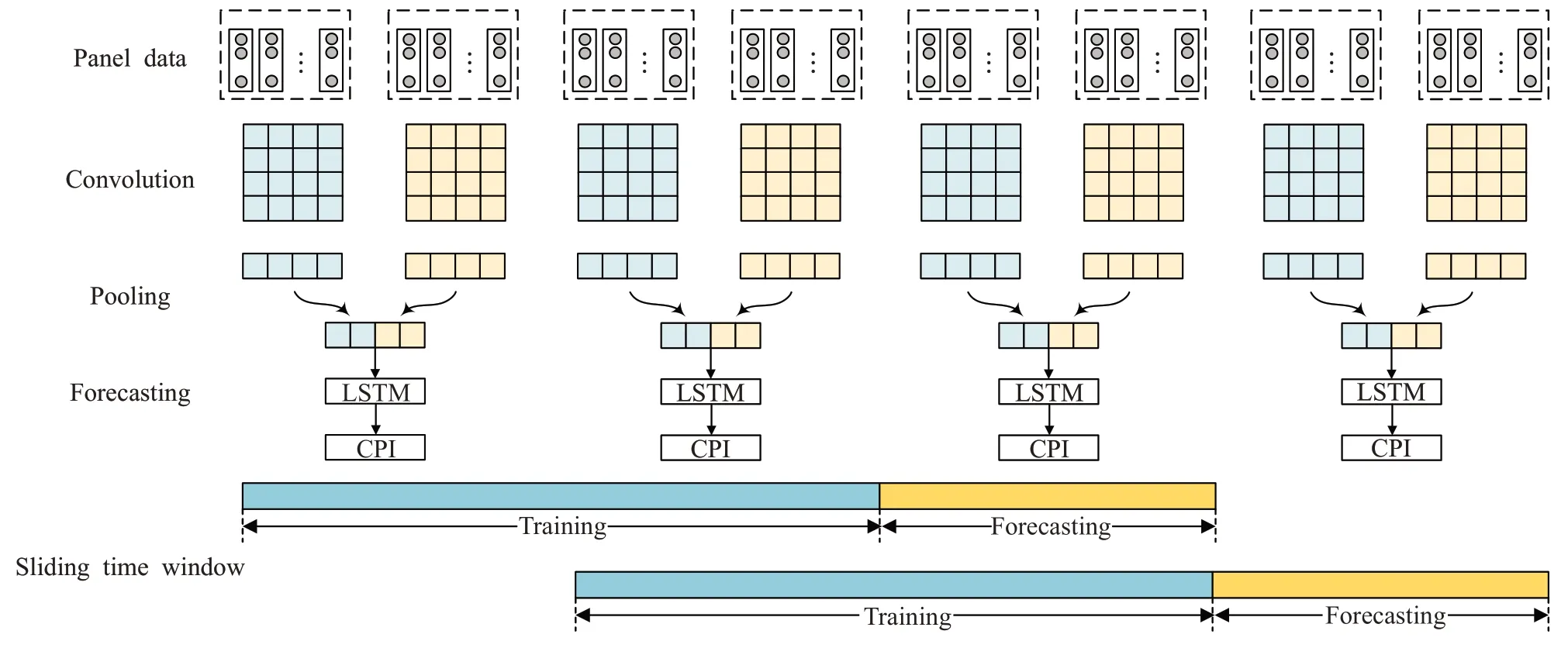
图3 CNN-LSTM深度网络预测CPIFig.3 Forecasting CPI based on CNN-LSTM deep neural network

2 实验与分析

2.1 数据预处理

本文选取了国内三大期货交易所包括上海期货交易所、郑州商品交易所和大连商品交易所的期货交易数据对模型进行训练。数据选取的时间范围从2010 年1月1日至2020年6月31日共计2 483个交易日。对期货合约的缺失数据按上一个交易日的数据补全。面板数据的每一列表示一个交易品种，每个品种选取次交割期、次近交割期和次次近交割期的合约。每种合约选取结算价、成交量、持仓量和未平仓量共四个特征。数据获取方面，期货日交易数据从国泰君安数据库获取；CPI数据从国家统计局网站获取；每月的CPI 采用环比CPI（上月=100），训练前对原始CPI 数据xt进行变换：(xt-100)/100。本文采用当月期货合约预测当月CPI是合理的，国家统计局总是在下个月的中旬公布上个月的CPI。

宏观数据的发布往往以月、季度或者年度为单位。本文针对宏观数据样本量稀疏的特点采用线性插值处理。这样做有两个优点：一是保持数据的趋势性。二是大大增加了深度网络训练样本的数量。用yt和yt-1分别表示t月和t-1 月国家统计局公布的CPI，函数U(·)将北京时间转换为Unix时间戳，则t月第k日的CPI的值采用线性插值计算：

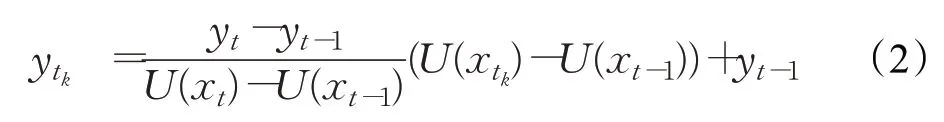
例如，国家统计局公布的2020 年3 月和4 月的CPI（环比，上月=100）分别为98.77 和99.14，采用线性插值计算得到2020 年4 月的每个期货交易日的CPI 的值如表1所示。

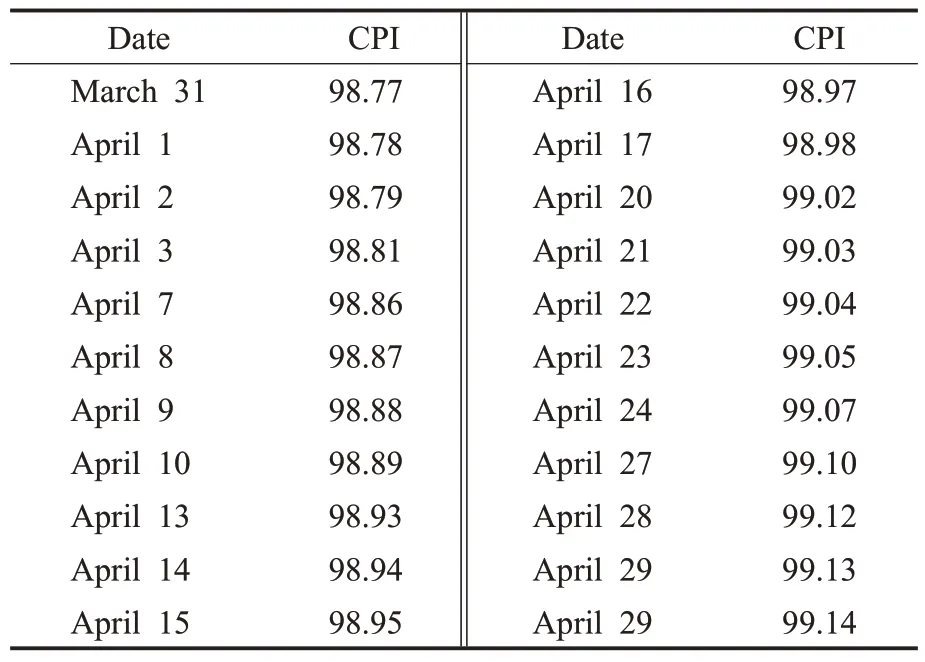
表1 2020年4月CPI插值数据示例Table 1 Example of CPI interpolated data（April 2020）

对宏观数据采用线性插值的方法，保留了原始数据的变化趋势，增加原始宏观数据样本数量的数量，为深度学习训练提供了较好的数据集。事实上，宏观数据在绘图过程中，默认了数据之间的变化是线性的。后续的实验中可以看到，线性插值数据对于传统的预测方法不会产生较大的影响。采用线性插值的方法，注意需要避免在tn时刻引入包含未来信息的训练集，这样做训练出来的模型不符合实际。例如在tn时刻，只允许使用tn时刻对应月份的上个月之前的CPI数据作为训练数据。

2.2 评价指标

本文的评价指标分为两类。一类是常用的评价指标，这类评价指标包括均方根误差（RMSE），平均绝对百分比误差（MAPE）和Pearson 相关系数R，用于评价模型的预测精度；另一类评价指标是本文设计引入的定向精度（directional accuracy，DA）指标，用以评价模型对于趋势预测的准确程度，以下分别予以说明。平均均方根误差（MRSE）表示为：

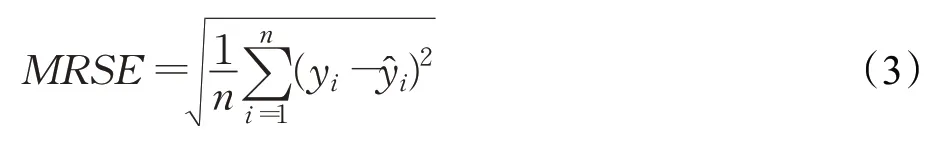
平均绝对百分误差（MAPE）表示为：

Pearson相关系数R表示为：

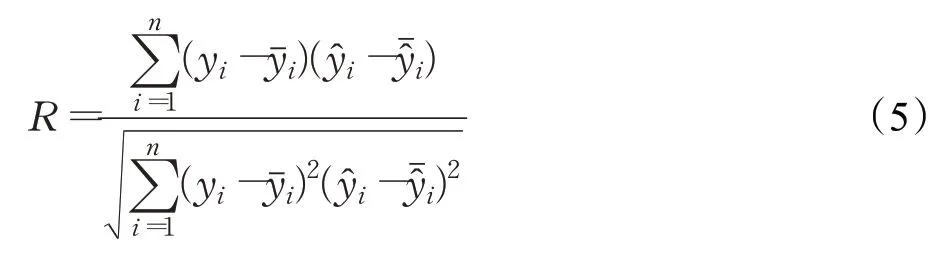
这三个评价指标用于评价模型的预测精度。为了评价模型对于趋势预测的准确程度，本文设计引入定向精度（directional accuracy，DA）指标。该指标用于评价模型对于时间序列趋势的预测的准确率，指标的计算方法如下：

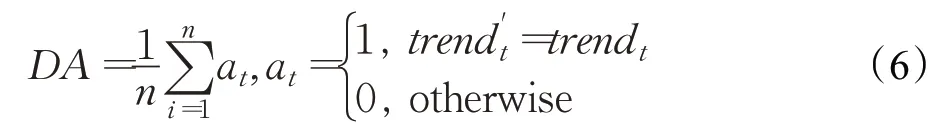
其中，trendt是CPI 预测的趋势。t时刻趋势定义为：

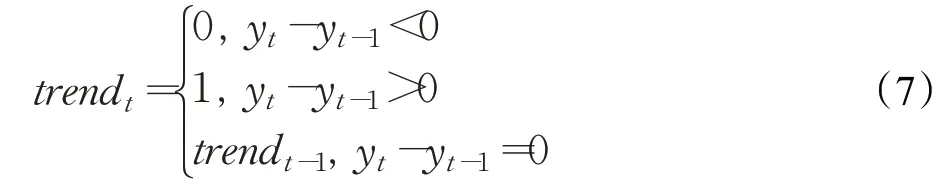
3 结果分析

本章实验主要分为三个部分，实验第一部分对模型的预测结果进行分析。第二部分将CNN-LSTM模型与SMR、ARIMA 和LSTM 模型进行对比分析。最后对模型进行稳定性分析，比较引入不同期货合约的CNNLSTM 模型对CPI 预测结果的影响。所有模型均采用2010 年1 月至2018 年12 月的CPI 数据作为训练集，2019年1月至2020年5月的数据作为测试集。

3.1 预测结果分析

模型预测2019 年1 月至2020 年5 月CPI 的结果如图4所示，实验对比了基于期货价格数据的CNN-LSTM模型预测结果和不含期货合约数据的CNN-LSTM模型预测CPI的结果。其中预测值1表示在不引入期货合约数据的情况下CNN-LSTM 模型预测CPI 的结果，此时模型对于CPI的趋势的预测仍存在较大偏差，引入期货数据以后，从预测值2 可以看到，CNN-LSTM 深度网络对未来一段时间内CPI的变化趋势做出了正确的判断，并且CNN-LSTM网络的预测精度也十分高。

3.2 实验结果对比分析

实验第二部分将CNN-LSTM深度网络的预测结果与支持向量回归、ARIMA、LSTM 模型的预测结果进行对比分析。不同模型的参数如表2所示。其中，SVR模型的核函数为RBF核函数[10]，ARIMA模型的参数为（1，0，0），在窗口滑动的过程中，CNN-LSTM深度网络总是以当前时刻对应月份之前的数据作为输入，以当前时刻对应的月份的CPI值作为输出。

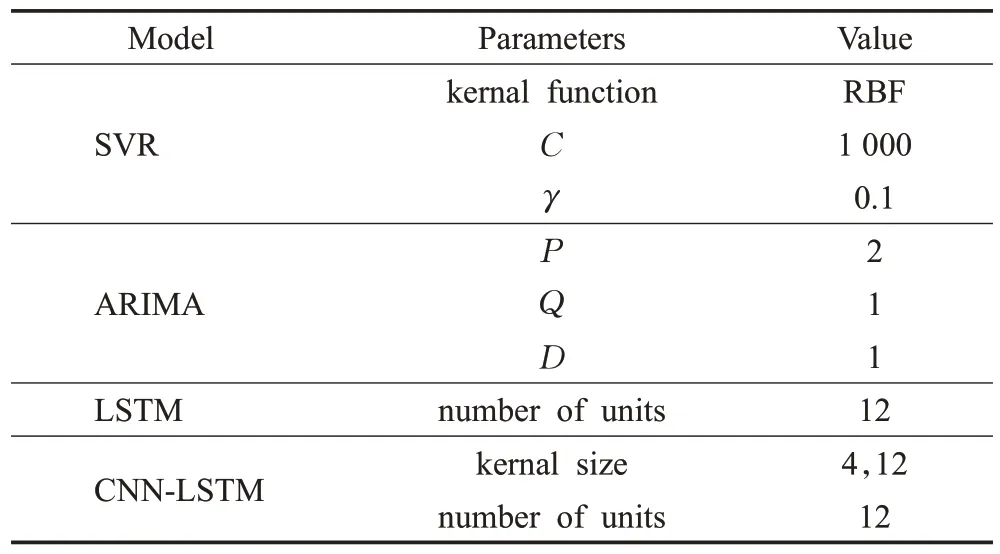
表2 CNN-LSTM深度网络、SVR、ARIMA和LSTM模型参数表Table 2 Parameters of CNN-LSTM deep neutral network，SVR，ARIMA and LSTM

图5展示了基于ARIMA、LSTM、SVR对2019年1月至2020 年5 月CPI 的预测结果。只关注模型在测试集上的表现情况。从预测结果可以看出，在2019年5月至2019年7月时间段内，ARIMA模型对CPI变化趋势的预测是十分准确的，预测精度也比较高。然而，在CPI波动比较剧烈的时间段（2019年9月至2020年5月），ARIMA模型的预测值相对于真实值的偏离比较大，且对CPI变化趋势的预测也不够准确。从图5 的结果可以得出LSTM 的CPI 预测的结果，LSTM 网络在部分时间段上（2019 年7 月11 月，2020 年2 月5 月）对CPI 变化趋势的判断是准确的，预测精度也比较高。和ARIMA 模型的表现相似的是，在部分时间段内，LSTM 的预测精度和趋势判断都不够理想（2019 年1 月至2019 年6 月）。从SVR（图5）的预测结果可以看出，在每一个时间点，SVR的预测值十分接近于上一个时刻的真实值，这表明SVR的预测值相对于真实值滞后，出现这种现象的本质的原因是CPI历史数据所包含的信息量有限，这也是大多数基于月度数据的模型容易遇到的问题，为了解决这样的问题，引入与CPI变动密切相关的日度信息是有必要的。

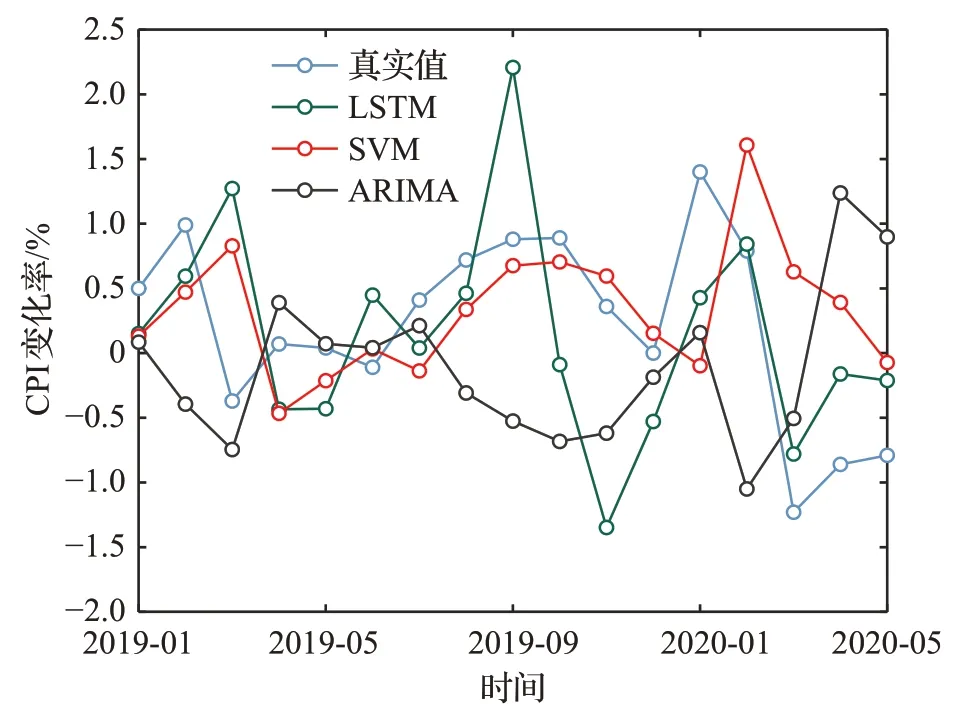
图5 CPI预测结果对比Fig.5 Comparison of CPI prediction results

表3对比了在不同评价指标下LSTM、SVM、ARIMA和CNN-LSTM 的精度和趋势精度。从表3 可以看到，CNN-LSTM深度网络预测结果的均方根误差（RMSE），平均绝对百分比误差（MAPE）分别为0.043 4和0.326 6，均小于其他三个模型。CNN-LSTM深度网络预测结果与真实值的Pearson相关系数R为0.992 5，呈现出高度的正相关性，定向精度DA为0.625 8，也优于其他三个模型的结果。CNN-LSTM深度网络利用月与月之间可观测到的期货市场的价格变动，发掘期货价格波动对于CPI 变化的影响，具有很好的期货价格发现能力和CPI预测能力。

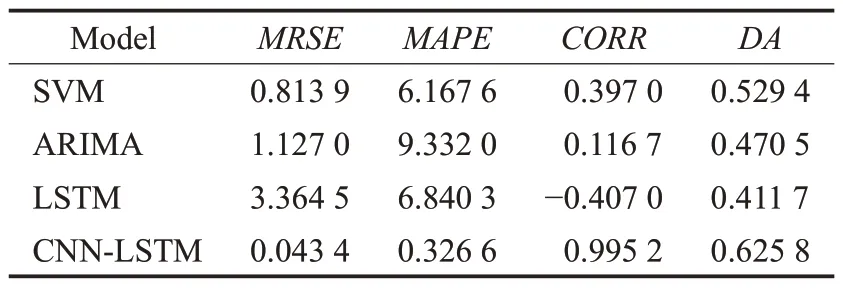
表3 模型预测结果的评价指标对比Table 3 Comparison of evaluation indicators of model prediction results

3.3 稳定性分析

实验的第三部分对CNN-LSTM模型进行稳定性分析。设计实验，对比模型在不同期货合约预测CPI的稳定性。分别测试在单一期货合约和多品种期货合约下模型的预测精度。由表4可以进行分析，当输入的期货合约品种在50 个以上的时，模型预测结果的平均绝对百分比误差、Pearson 相关系数和定向精度均保持在较为稳定的区间，这表明模型的预测具有一定的稳定性。当期货品种数量少于40，模型预测值的平均绝对百分比误差有较为显著的上升，且Pearson 相关系数和定向精度均有下降。在期货品种较少的情况下，数据所包含的信息有限，使得模型较难对CPI提供精确的预测。从以上结果可以得出，当期货合约数据的样本数量保持在一定的水平，本文模型结构能对CPI 提供较为精确的预测，这表明模型具有一定的稳定性。

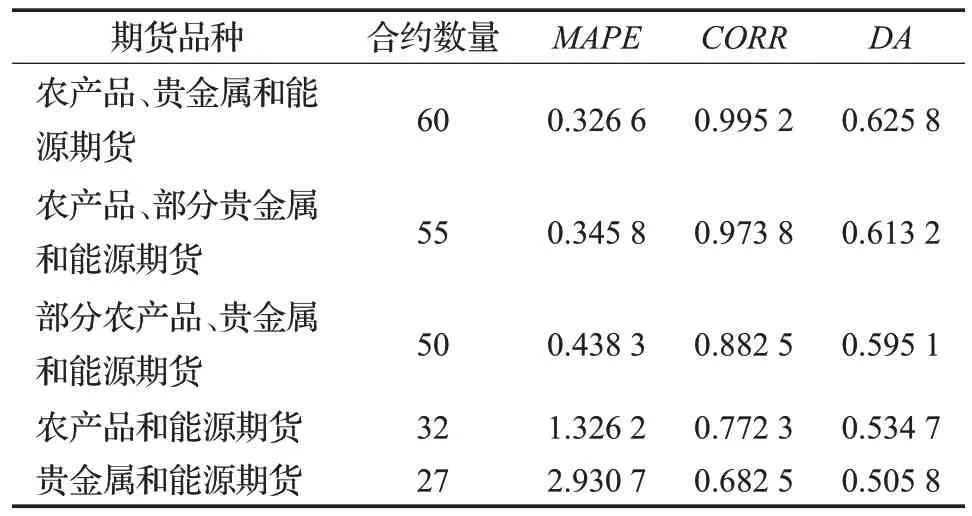
表4 不同种类期货合约预测结果分析Table 4 Analysis of forecasting results with different future types

4 结束语

科学预测我国CPI 并在此基础上运用一定的技术手段，实施超前性的货币政策，对于全面把握经济发展趋势、经济安全以及社会稳定具有重要的意义。期货的价格变动是通货膨胀更早期的预警指标，它包含基础商品价格的波动会影响生产者价格指数，进而影响消费者价格指数。CNN 具有特征提取和特征识别的特点，被广泛应用于空间特征提取；LSTM网络具有处理时序相依数据的能力，本文选取期货日交易数据，结合卷积神经网络（CNN）和长短期记忆（LSTM）网络的特点，提出基于CNN-LSTM 深度网络的CPI 预测模型，进行期货面板数据特征提取和CPI 预测。论文针对CNN-LSTM深度网络训练过程中存在两种影响模型训练效果的问题，一是梯度消失导致神经网络难以收敛，二是过拟合导致测试集失效，本文在设计训练网络时添加BN层效解决了梯度消失问题，通过Dropout 技术阻止神经元共适应缓解决了过拟合问题。CPI 数据是以月为单位发布的，数据量相对较少，为解决训练过程中存在样本数量不足的问题，本文对月度CPI 数据进行插值处理，提高深度网络训练样本量。论文设计实验实现了CNNLSTM 深度网络，将预测过程分为两个阶段，一是预训练阶段，二是动态训练预测阶段；通过滑动时间窗口对网络进行训练并对未来一段时间的CPI做出预测；将预测结果与支持向量回归、ARIMA 和LSTM 模型进行对比分析，结果表明CNN-LSTM 预测结果的各项评价指标，包括MRSE、MAPE、Pearson 相关系数和DA 均优于传统方法预测的结果，当期货合约数据的样本数量保持在一定的水平，本文的模型结构能对CPI提供较为精确的预测。研究表明，本文提出的CNN-LSTM深度网络具有很好的价格发现能力，对于CPI早期预警具有意义。