融合多策略的鸟群算法及油层识别ELM模型优化

宋 飞，夏克文，杨文彪

河北工业大学 电子信息工程学院，天津300401

群体智能是相对高效的一种优化算法，它可以解决传统技术难以解决的非线性问题以及NP难等问题。因此，群体智能算法得到了广泛的研究和关注。蜻蜓算法的主要灵感源于自然界中蜻蜓的静态和动态蜂群行为[1]。通过自然界中的鸟类的觅食、警惕、飞行三种行为，Meng等人对于鸟类的交互行为进行建模分析，提出了一种新型的群智能算法，即鸟群算法（BSA）[2]。虽然群体智能算法具有简单高效，易于实现的优点，但它在实际应用中依然存在易于陷入局部最优等缺点。因此，对于群体智能算法的改进越来越重要。Zhang 等人提出了一种动态多群差分学习量子鸟群算法来融合三种策略来提高鸟群算法的性能[3]。Wang 等人通过扰动局部最优解的策略，使原鸟群算法又快又稳地收敛到全局最优[4]。Wang 等人采用正弦函数和余弦函数来控制加速系数，改变了空间搜索，使全局最优值收敛更快[5]。由此可见，多种改进策略相结合的方法具有一定的效果。

群体智能优化算法大多存在易于陷入局部收敛以及收敛精度低等局限性，鸟群算法同样具有这些缺点，采用多种改进策略结合的方式对鸟群算法进行改进，提出融合多策略的鸟群算法（MMSBSA）。首先，为了增强算法跳出局部最优的能力，提出混沌参数和高斯扰动策略；其次，为了加快算法的收敛速度，引入混合多步选择和自适应步长策略；最后，为了增加种群的多样性，提出小波变异策略，增强算法的寻优能力。为验证改进算法的有效性，将改进算法与另外5 种智能算法进行比较，选用10个基准函数测试算法的性能。

极限学习机（ELM）是单隐层前向网络的训练算法，具有训练速度快，泛化性能高的特点，广泛应用于回归于分类问题之中。因此，考虑将ELM 应用于油层识别中。由于ELM 隐含层参数是随机选取的，所以其稳定性较差，因此对于ELM的参数优化必不可少。目前，王珂珂等人[6]应用鲸鱼算法优化ELM，牛春彦等人[7]提出用云量子花朵授粉算法来优化极限学习机，但算法的收敛精度较低，模型泛化性不高。采用MMSBSA 对极限学习机模型进行参数优化，应用油层识别实验验证改进的极限学习机的识别效果。

1 鸟群算法及其改进

1.1 鸟群算法

鸟群算法是Meng等人[2]在2015年提出的一种新型的生物启发式算法，通过模仿鸟类的社交行为及互动中的觅食行为，警惕行为和飞行行为来解决优化问题。

设鸟群规模为N，飞行空间维度为D，(i∈[1,2,…,N])代表鸟的位置，FQ表示飞行间隔，P为觅食概率，若(0,1) 间的随机数小于P，鸟类将会选择觅食，否则，这只鸟将继续保持警惕。

（1）觅食行为

每只鸟通过自我经验和群体经验来寻找食物，用数学公式表示如下：

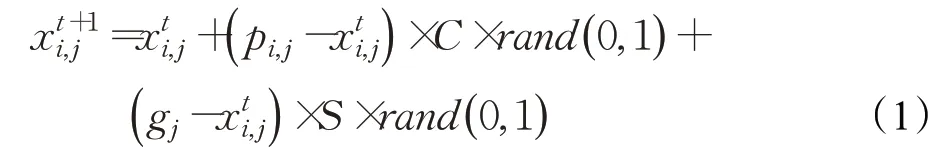
其中，j∈[1,2,…,N]，rand(0,1)表示(0,1)中的独立均匀分布数，C和S为自我认知和社会认知加速系数，pi,j是第i只鸟的最佳先前位置，而gj是种群共享的最佳先前位置。

（2）警惕行为

鸟类试图移动到种群的中心，并且它们将相互竞争，用数学公式表示如下：

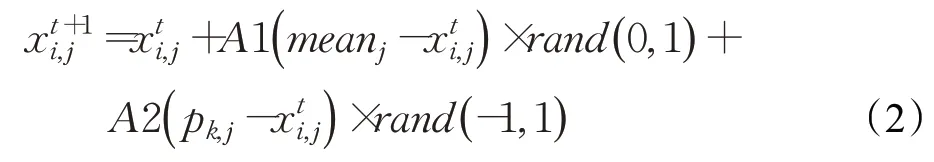
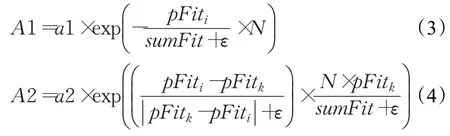
其中，k(k≠i)是从1到N之间的随机整数，a1 和a2是中的两个常数，pFiti代表第i只鸟的最佳适应度，sumFit表示种群的最佳适应度之和，meanj表示整个群体平均位置的第j元素，ε用于避免零分误差，是计算机中的最小常数。

（3）飞行行为

当鸟类到达一个新的地点进行飞行行为时，会划分为生产者和乞食者，用数学公式表示如下：

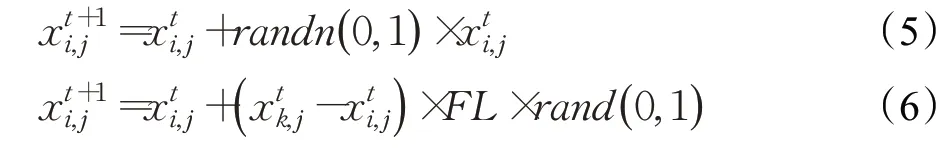
其中，randn(0,1)表示均值为0，标准差为1的高斯分布随机数，k∈[1,2,…,N],k≠i，FL(FL∈[0,2])表示跟随概率。

1.2 改进的鸟群算法

目前，鸟群算法在优化问题中的应用效果显著，具备调节参数少，鲁棒性能好，收敛精度高等优点，但是依然存在收敛速度缓慢，多样性不足，局部收敛等问题。因此，本文对于鸟群算法进行了深入研究，提出了五种改进策略，用以提高鸟群算法的性能。

1.2.1 混沌参数

混沌变量具有遍历性、有界性和普适性的特点，许多学者将混沌应用于群体智能算法的搜索空间的初始化之中，取得了显著的效果。由此，依据混沌序列固有的规律性，将其引入到鸟群算法的参数之中。

受PSO 算法的启发，在鸟群算法中引入惯性权重。权重具有混沌序列的遍历随机性，为了有效地增强算法的全局搜索能力，提高算法跳出局部最优的能力，在鸟群算法的觅食行为之中引入Ding等人在鲸鱼优化算法中提出的混沌惯性权重[8]，如公式（7）所示：

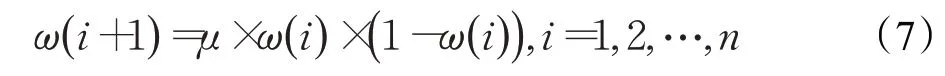
其中，μ的值为4时，logistic混沌具有稳定的状态。

通常，鸟群算法中的两个加速系数会设置为相同的常数。为了平衡算法在全局和局部的搜索能力，在鸟群算法中引用了Du等人对于PSO算法中的认知成分和社会成分改进的对称切线混沌加速系数[9]，加速系数C、S如公式（8）、（9）所示：

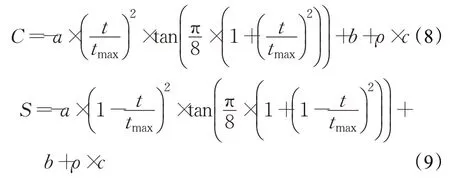
其中，a、b、ρ的值为0，2 之间的常数，t是迭代次数，tmax是最大迭代次数，c是满足logistic混沌的映射。

通过多次实验验证，a的值为0.5，b的值为1.5，ρ的值为0.1。

将引入的混沌参数加入到鸟群的觅食行为中，提出混沌鸟群算法（CBSA），改进如公式（10）所示：

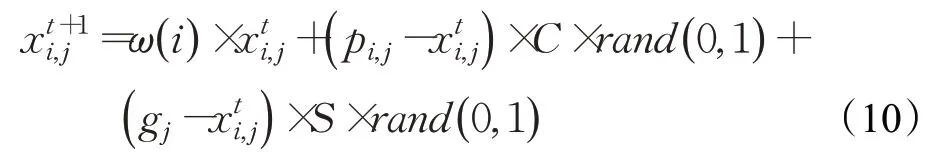
1.2.2 高斯扰动

针对算法的种群多样性不足，容易陷入早熟收敛的情况，受文献[10]和文献[11]的启发，在鸟群的觅食行为中增加高斯扰动策略，增强个体的逃逸能力，促使算法跳出局部最优，提出混沌高斯鸟群算法（CGBSA），改进如公式（11）所示：

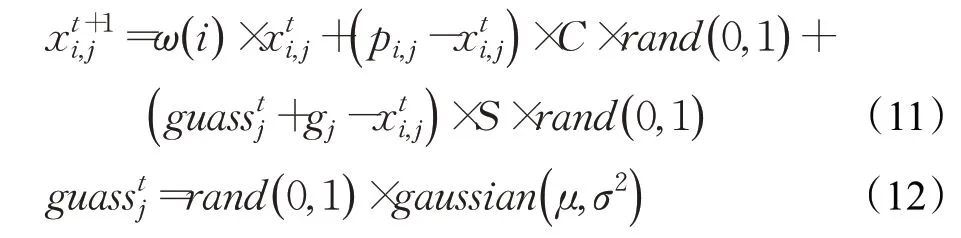
1.2.3 混合多步选择

为了增强算法种群的多样性与随机性，加快算法的收敛速度，受Du等人[9]对于PSO算法改进方法的启发，将混合多步选择策略引入鸟群算法中，考虑将基本算法未搜索的位置点引入寻优的选择范围之中，将个体位置更新分为四部分，为了加快算法的收敛速度，比较各个位置的适应度函数值选择最优的位置。提出混沌高斯多步鸟群算法（CGMBSA），策略描述如下：

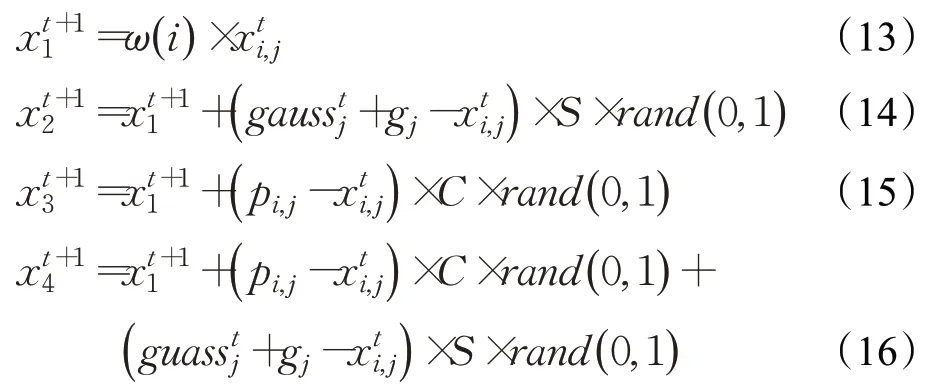
然后根据个体位置的适应度大小选出最佳位置，过程如公式（17）所示：

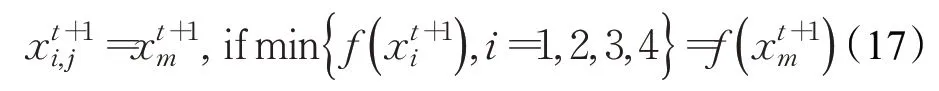
1.2.4 自适应步长

针对鸟群算法收敛速度慢的缺点，受文献[12]的影响，将基本鸟群算法飞行行为中的随机步长设置为自适应步长，步长因子随迭代次数的增大而减小，提出混沌高斯多步自适应鸟群算法（CGMABSA），改进如公式（18）、（19）所示：

其中，λ为0，1 之间的常数，t为迭代次数，tmax为最大迭代次数。

通过多次实验发现λ的取值为0.000 1 时，可以得到较好的实验效果。

1.2.5 小波变异

受文献[13]的启发，为了增加算法种群的多样性，引入小波变异策略，对于适应度小于种群平均适应度的个体位置进行变异操作，变异过程如公式（20）所示：

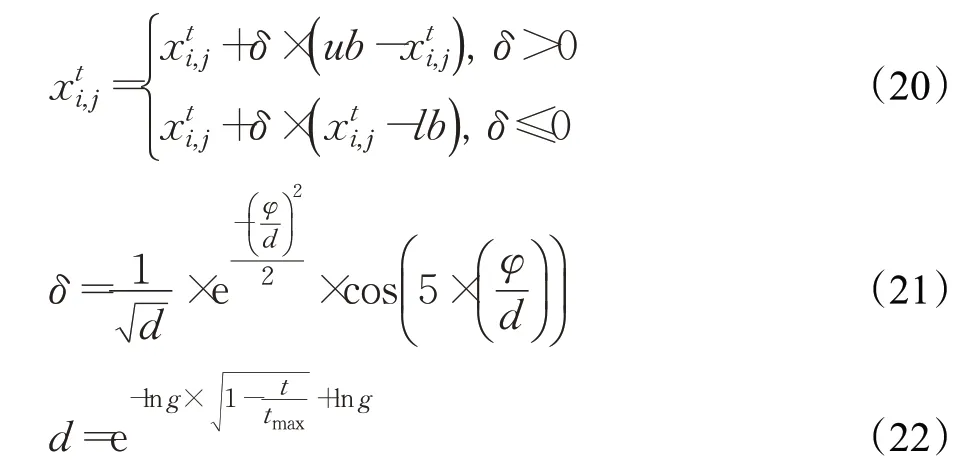
其中，ub为变量上边界，lb为变量下边界，防止算法超出搜索范围，φ为[-2.5d，2.5d]之间的随机数，g的取值为10 000，t为迭代次数，tmax为最大迭代次数。

综上所述，将融合五种改进策略的算法命名为融合多策略的鸟群算法（MMSBSA），MMSBSA 算法步骤如下所示。

1.3 仿真实验与分析

为了验证MMSBSA 的有效性，选取10 个基准函数[14]进行测试，如表1所示，其中，F1～F4为单峰函数，仅有一个最优值，可以用来验证算法的收敛性能；F5～F7为固定维多峰函数，F8～F10为混合维多峰函数，包括多个局部最优解。

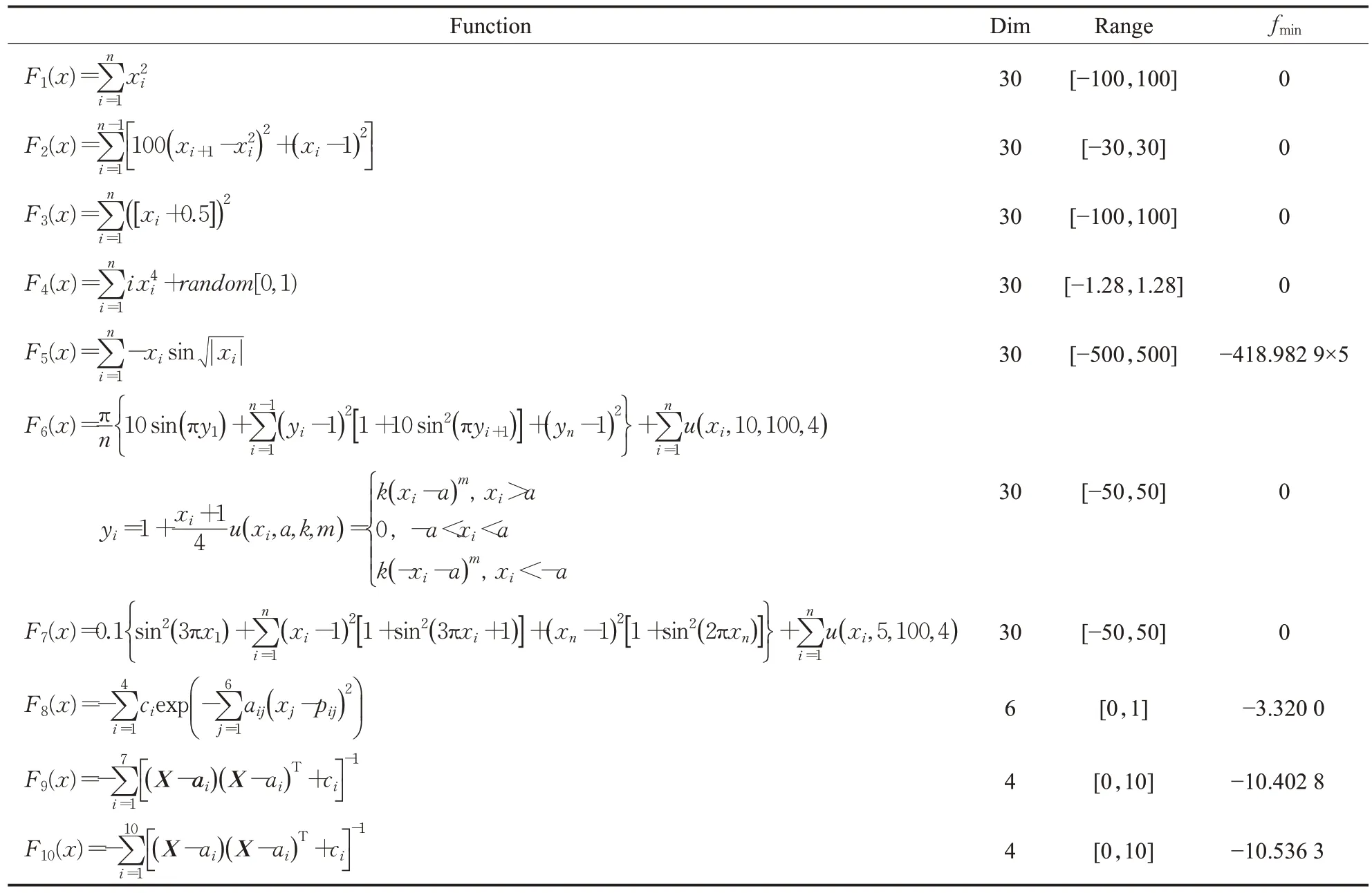
表1 10个基准函数Table 1 10 benchmark functions

本文的实验环境如下：MATLAB R2018a，Win10（64 bit），PC 处理器是Intel®Core™i5-10300H，主频是2.5 GHz，内存是8 GB。所有优化算法的种群规模为30，最大迭代次数为1 000，各算法的参数设置如表2 所示。为了保证算法的有效性，以下所有实验都在相同的条件下进行。

表2 优化算法参数设置Table 2 Parameter setting of optimization algorithm

首先，为了验证融合多策略的鸟群算法策略的有效性，进行了消融实验进行比较。为了验证策略的有效性，通过BSA 与各种改进的鸟群算法进行比较分析。仿真寻优迭代曲线如图1所示。

由图1可知，本文的改进策略在单峰、多峰以及混合多峰函数的测试中，均可以取得优于基本BSA的效果。其中，CBSA与CGBSA的效果相较基本BSA来说，具有一定的跳出局部最优的能力；CGMBSA 和CGMABSA的寻优曲线相较于CGBSA来说，寻优速度更快，而且通过对比分析，MMSBSA的寻优效果最佳，说明本文改进策略的融合具有一定的效果。

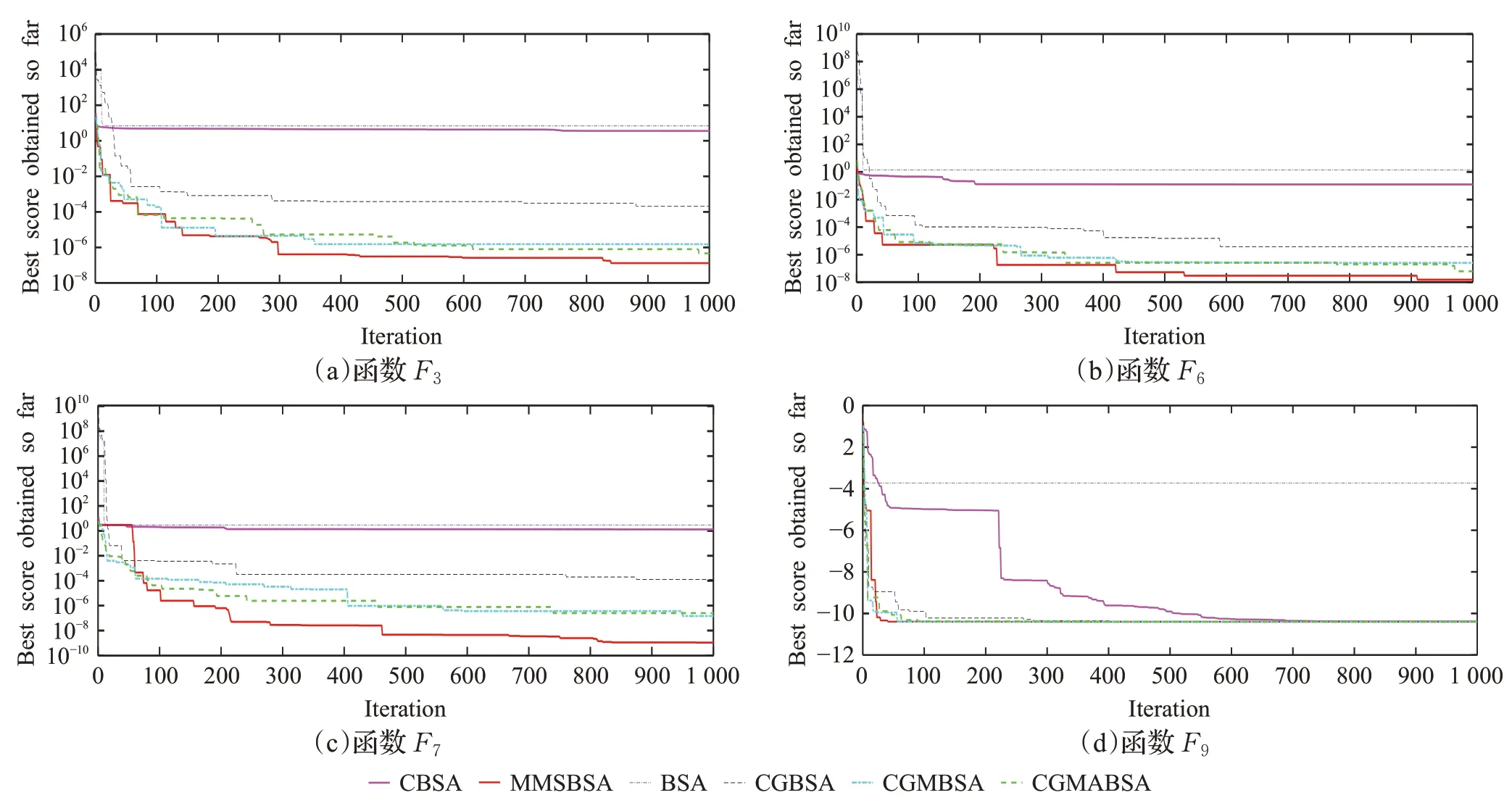
图1 4个基准测试函数的仿真寻优迭代曲线图Fig.1 Iterative curves of simulation optimization for four benchmark functions

其次，将MMSBSA 与BSA、鲸鱼算法（WOA）[14]、正弦余弦算法（SCA）[15]、具有时变加速系数的粒子群优化算法（TACPSO）[16]、文献[17]中改进的粒子群算法（MPSO）进行对比分析，验证MMSBSA的性能。

为了更加直观地观测各算法的性能，10个基准测试函数的仿真寻优迭代曲线图，如图2所示。

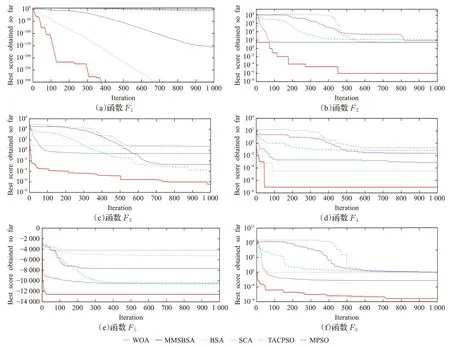
图2 基准测试函数的仿真寻优迭代曲线图Fig.2 Iterative curve of simulation optimization for benchmark function

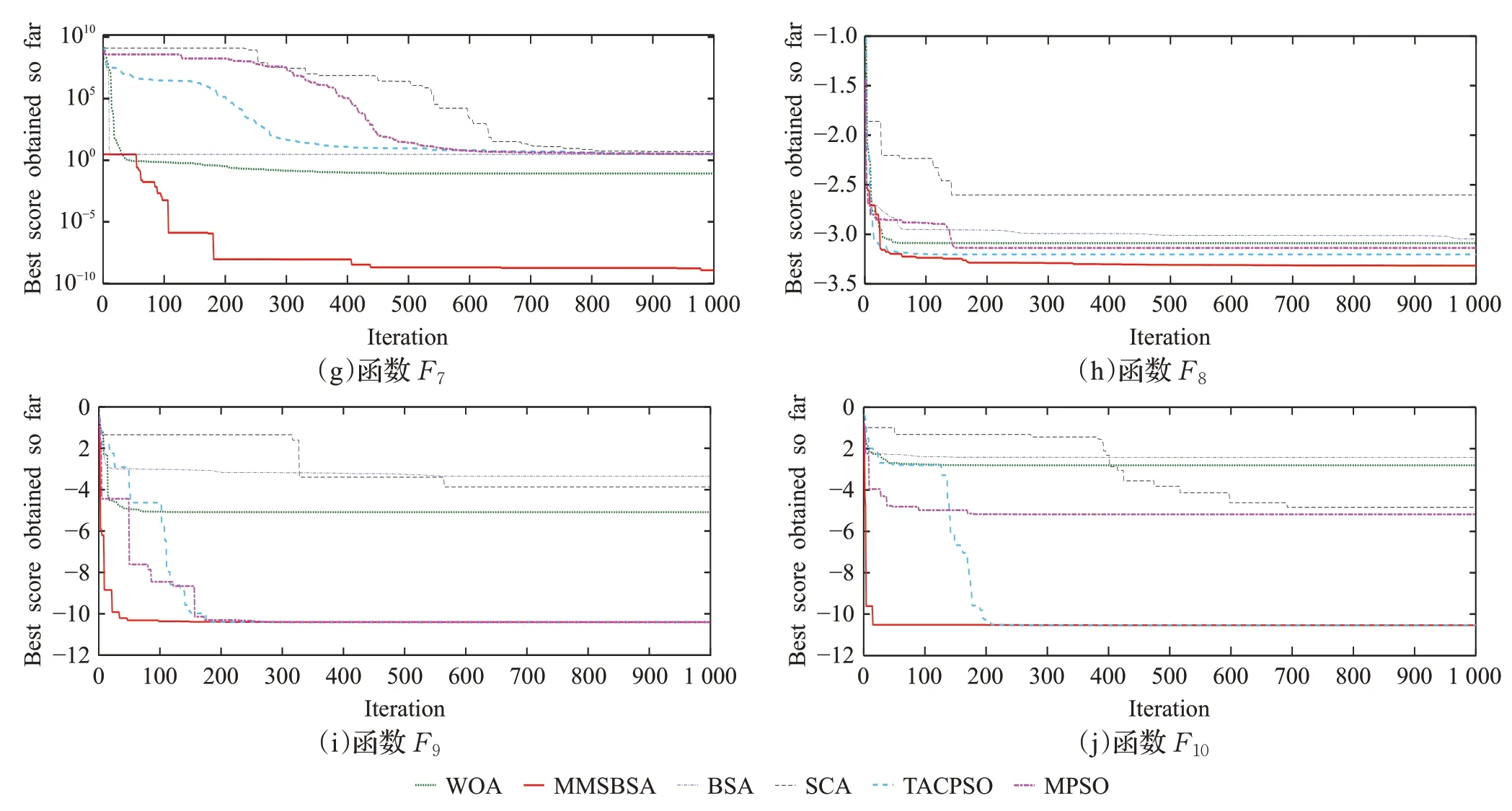
图2 （续）

图2中实线为MMSBSA算法迭代寻优曲线，图2中的（a）～（d）是单峰基准函数的寻优曲线，在F1函数寻优中，WOA、SCA、TACPSO 和MPSO 都存在一定的早熟收敛情况，BSA 和MMSBSA 的收敛速度随着迭代次数的增加而加快，而且都能够寻找到最优值，其中，BSA的寻优趋势近似于线性收敛变化，横坐标为690时达到最小值；而MMSBSA在迭代前期收敛很快，图中横坐标为130 时成拐点开始趋于平缓，横坐标为378 时达到最小值。显然，MMSBSA 的寻优速度更快。在函数F2、F3、F4的寻优曲线中，MMSBSA 不仅寻优速度快于其他算法，而且寻优精度也高于其他算法。图2中的（e）～（j）是多峰基准函数的寻优曲线，对于多峰函数的测试，MMSBSA性能依然优于其他对比算法。

综上所述，本文对于鸟群算法的改进具有积极的影响，MMSBSA对于基准函数的测试效果优于其他5种智能算法。

为了更加全面地验证算法的有效性，获得每个算法运行30 次的平均值、最大值、最小值以及标准差，10 个基准测试函数的评价指标结果如表3所示。

表3 中粗体标出的为最优的结果，由表3 可知，MMSBSA 无论是单峰函数，还是多峰函数的寻优结果都比较接近最优值，而且寻优能力在多数情况下高于另外5 种算法，算法性能比较稳定。因此，可以验证MMSBSA在收敛速度以及寻优精度方面的性能高于其他算法。

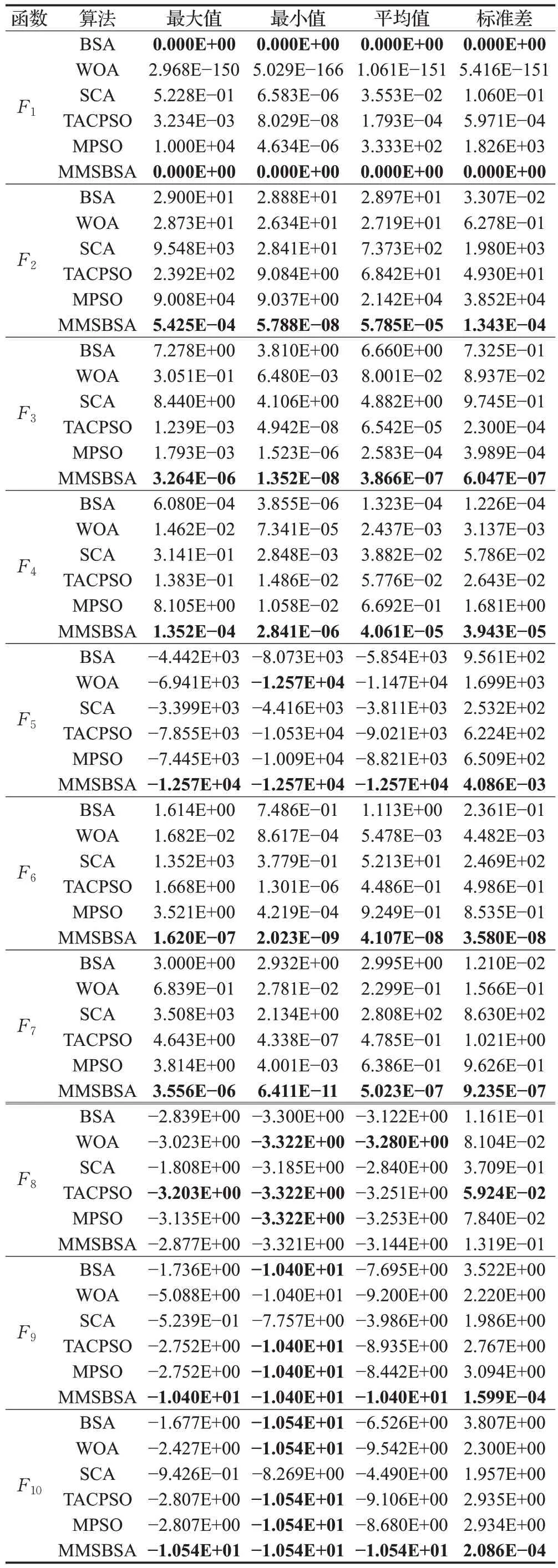
表3 不同算法的测试结果Table 3 Test results of different algorithms

2 改进的极限学习机模型

2.1 ELM原理

极限学习机是Huang 等人[18]针对单隐藏层前馈神经网络提出的一种新的学习算法，极限学习机比人工神经网络更加简单、训练速度较快、泛化性能好。

ELM的数学模型[18]如公式（23）所示：

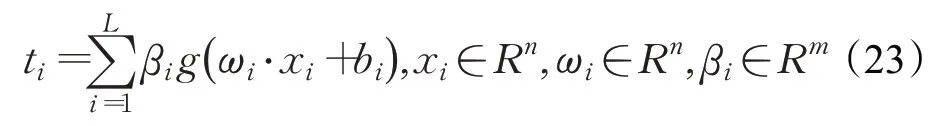
其中，ti表示输出结果，βi表示隐含层与输出层的权值，bi表示隐含层的偏置，xi表示样本数据，假设有q个样本。

本文应用的激活函数为Sigmoid 函数，如公式（24）所示：

公式（23）可以写成：

公式（25）可以转换为最小二乘解问题：

其中，H+是H的Moore-Penrose 广义逆矩阵。

2.2 MMSBSA-ELM模型

在基本的ELM中，随机选取参数导致ELM的分类准确度不高，性能不稳定。MMSBSA具有收敛精度高、速度快、稳定性强的优势。因此，采用MMSBSA 优化ELM模型的权重ω和偏置b，选出最优值，代入ELM中进行训练，构建MMSBSA-ELM 模型。MMSBSA-ELM模型算法步骤如下所示。

算法MMSBSA-ELM模型算法

3 油层识别的MMSBSA-ELM模型应用

油层识别是石油开发与勘探的主要任务，为了提高ELM模型的分类精度，将MMSBSA用于油层识别ELM模型的参数优化，通过某油田实际数据来验证模型的性能。

选取两个实际的油井数据对油层识别MMSBSAELM 模型进行应用测试。A1、A2 均为国内某油井，A1井测得13 个属性信息，分别为{GR，DT，SP，WQ，LLD，LLS，DEN，NPHI，PE，U，TH，K，CALI}，经过约简之后得到{GR，DT，SP，LLD，LLS，DEN，K}7个属性信息；A2井实际测得28 个属性信息，分别为{AC，CNL，DEN，GR，RT，RI，RXO，SP，R2M，R025，BZSP，RA2，C1，C2，CALI，RINC，VCL，VMA1，VMA6，RHOG，SW，VO，WO，PORE，VXO，VW，SO，AC1}，经过属性约简之后得到{AC，GR，RT，RXO，SP}5个属性信息，对于约简后的信息进行归一化处理，公式如下所示：

其中，x为样本属性值，xmin表示样本属性的最小值，xmax表示样本属性的最大值。图3 为A2 井约简后的5个属性信息在井段1 255～1 280 m的归一化处理结果。

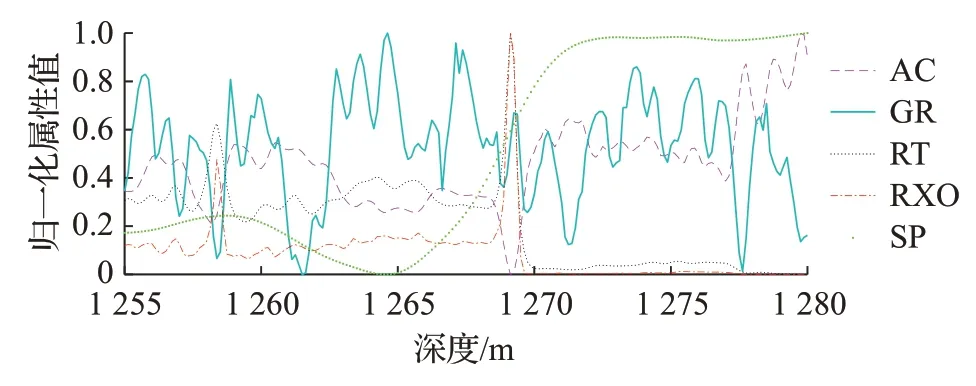
图3 属性归一化曲线图Fig.3 Attribute normalization graph

在A1井的井段3 330～3 350 m中提取201个样本数据点，其中油层样本点有84个，非油层样本点有117个，然后将样本点随机划分为两部分，训练集用来训练构建网络模型，测试集用来验证模型的性能。

对于分类问题来说，激活函数选取Sigmoid 函数的ELM 分类效果最好，因此，本文的激活函数选取Sigmoid函数，隐含层节点数选取35。

为了验证MMSBSA-ELM模型的性能，选取遗传算法（GA）、粒子群算法（PSO）、蚁群算法（ACO）优化的ELM以及基本的ELM与MMSBSA-ELM的性能进行比较，各优化算法的参数设置为GA 的交叉概率为0.7，变异概率为0.05；PSO 的ωmax=0.9，ωmin=0.5；ACO 的信息素蒸发系数为0.5，转移概率为0.5，所有种群的最大迭代次数设置为200。识别准确率选取每个算法运行20次之后的平均值，A1井的各算法识别准确率如表4所示。

表4 ELM算法性能比较Table 4 Performance comparison of ELM algorithms

由表4可知，MMSBSA-ELM具有较高的识别率，可达到97.18%，这说明MMSBSA的优化提高了ELM的分类精度，分类效果显著。

选取A2 井的样本信息来验证油层识别MMSBSAELM模型的性能，A2油井数据信息如表5所示。

表5 A2油井数据信息Table 5 Data information of well A2

通过A2井的样本数据信息来验证MMSBSA-ELM模型的有效性，A2井的真实油层分布和各个ELM的分类结果如图4 所示。其中，横轴代表油层深度，纵轴代表类别标签，“1”代表油层，“0”代表非油层。

由图4可知，与ELM、GA-ELM、PSO-ELM和ACOELM的识别结果相比，MMSBSA-ELM的识别结果最为接近真实的油层分布。为了评估油层识别模型的性能，采用以下指标：

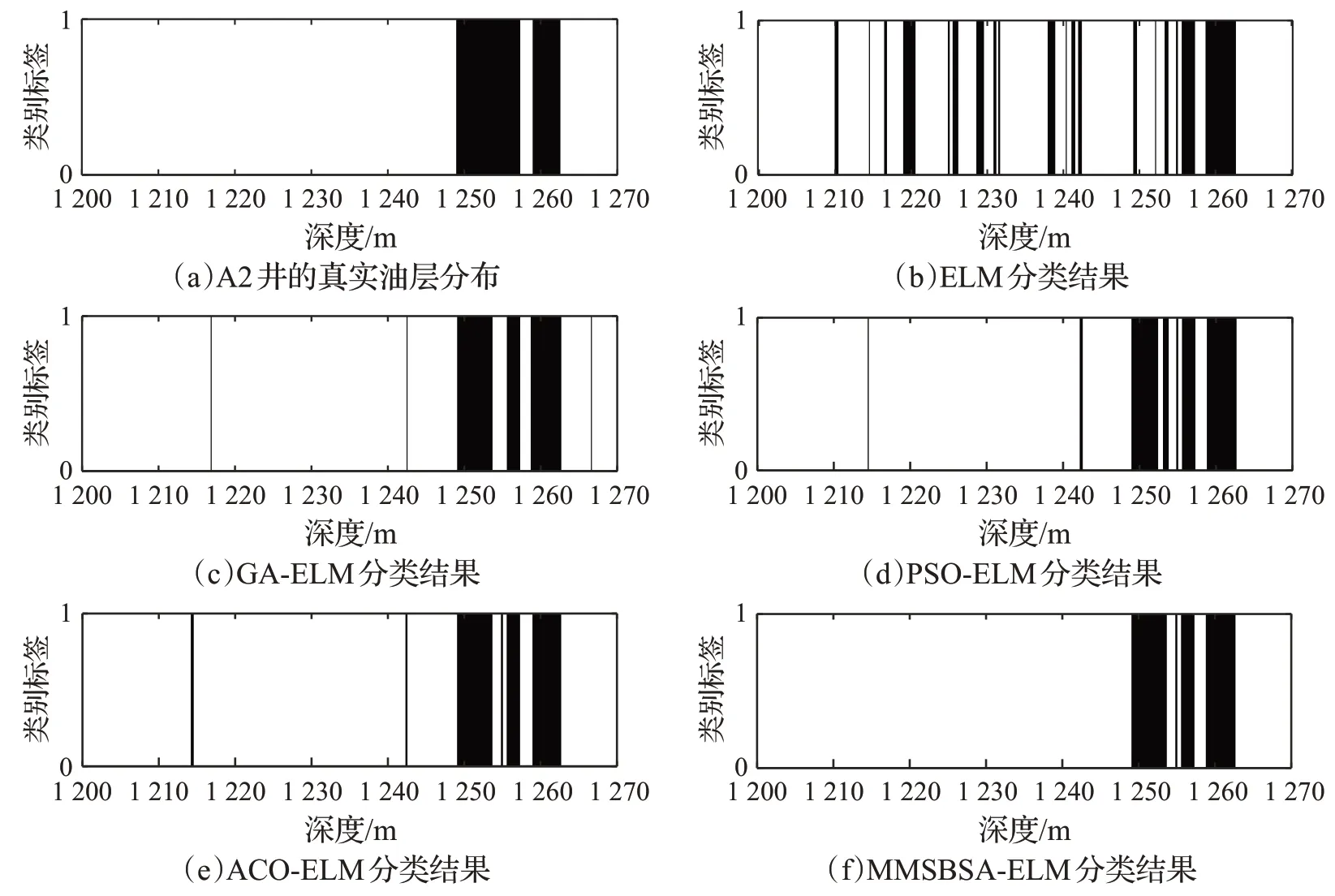
图4 真实油层分布和ELM分类图Fig.4 Actual oil layer distribution of A2 and classification of ELM

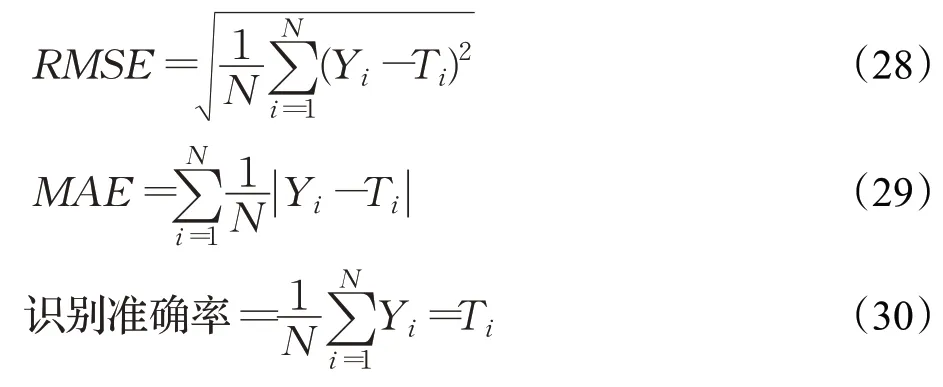
其中，Yi和Ti分别表示识别输出值和期望输出值，RMSE 可以评估分类识别模型的准确度，MAE 可以显示识别模型的预测误差。

为了展示各个模型的性能，表6是各算法运行20次取平均值的结果。

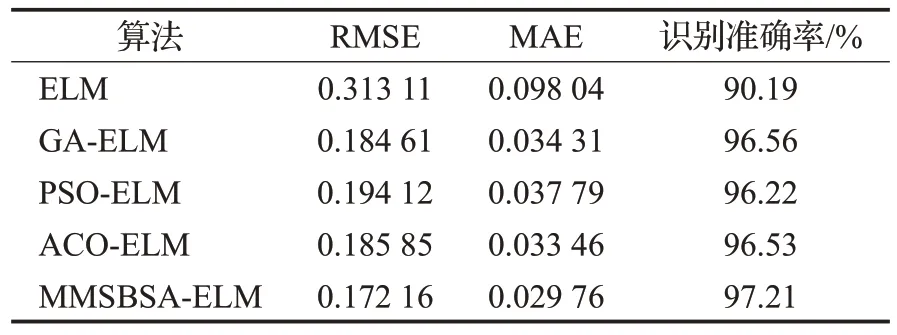
表6 ELM算法性能比较Table 6 Performance comparison of ELM algorithms

由表6可知，在A2井井段的油气层识别中，MMSBSAELM的平均识别准确率可达97.21%，高于其他对比模型的识别结果，预测误差也低于其他模型，说明MMSBSAELM模型在样本点较多的情况下依然具有较高的识别准确度，具有一定的应用价值。

4 结束语

本文提出的融合多策略的鸟群算法，即MMSBSA，引入混沌参数和高斯扰动策略，增加算法的寻优能力，提高算法跳出局部最优的能力；混合多步选择策略和自适应步长策略的融合，能有效地加快算法的收敛速度；小波变异策略，可以增加种群的多样性。通过10 个基准函数测试，与BSA、WOA、SCA、TACPSO 和MPSO 这5种智能算法进行比较，MMSBSA具有更加精准快速的寻优性能。将MMSBSA 应用于ELM 模型的参数优化中，即建立油层识别MMSBSA-ELM 模型，应用于油层识别领域，与ELM、GA-ELM、PSO-ELM 和ACO-ELM的识别结果相比，MMSBSA-ELM的识别准确率高于其他模型，这表明改进方法具有一定的可行性，具有实际应用价值。