一种运动链拓扑对称性识别方法

吴昌军，邓涛，许辉，张露

（1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.重庆交通大学 航空学院，重庆 400074）

对运动链进行综合是获得机械装置新构型的主要途径之一[1-2]。在过去几十年里，许多有效的综合方法被陆续提出。运动链之间的等效结构即同构被认为是此过程中的一个主要难题，为此学者们对其展开了大量研究[3]。然而顶点（构件）的等效结构即拓扑对称性顶点在一定程度上被忽略，但这并不意味着拓扑对称性没有研究的价值[4]。事实上，识别同一链中的拓扑对称性不仅能加快运动链的综合，而且有助于机构的枚举[5]。

群论法[6-7]主要以排列组合为理论基础来识别构件的对称性，原理简单，有效性高。然而对于一个n杆链来说，顶点标号的排列有n!种，并且排列的数量会随着顶点的增加而显著增加。尽管这些群论法都提出了一套属于自己的准则来减少不必要的排列，但在某些情况下，排列的数量仍然是惊人的。构件的完全关联链表法[8]是通过对邻接构件的层层嵌套来获得某一构件的唯一表示。此方法有效性非常高，但构件的完全关联链表是一个结构量而非数值量，并且当n较大时，此链表的结构非常复杂而且冗长。对比两构件的链表需要比较两表的层数以及层数中各邻接构件的组成情况，这意味着此过程将耗费较多的时间。关系码法[9-10]是将某一顶点相邻接的各顶点的权值按大小排列以形成此顶点的识别码，比完全关联链表法更简单、更高效。一级关系码的权值为顶点的度，二级码的权值为一级码，以此可推广到更高阶的关系码。然而杆件数量越大，判定所需的关系码级数也越高。级数的增加会导致其长度的显著增加，一些10 杆拓扑图的IV 级码已经达到60 多位，更重要的是该方法在某些情况下已经出现误判。一种基于广度优先生成树的方法[11]是通过比较构件广度生成树的结构特征来进行构件的对称性判定。它计算量小，便于计算机实现，然而当构件数量较大时，广度优先搜索算法的内存耗量较大。重标法[12]是根据提出的一些特定的规则对运动链重新标号，随后对新旧矩阵进行对比判定对称性。这种方法可靠性较高，对判定条件的充分性有足够的理论依据。然而这些重标规则十分复杂和繁琐，涉及大量抽象概念，并且可能会出现好几种重标的可能，此时效率相对较低。三次幂向量序列（Cubic power vector sequence，CPVS）法[13]是利用邻接矩阵的三次幂序列作为构件的不变量。它效率高，复杂度低，但在判定某些复铰时会出现误判。连杆邻接串法[14]是一种将汉明矩阵简化表示为数字串来识别构件对称性的方法，效率高，计算简单。但对于度较大的构件来说，连杆邻接串非常长，尤其是在大型运动链的情况下。此外，如果一阶汉明连杆邻接串失败，需要二阶汉明邻接串，这使得判定过程变得更加复杂。连杆识别码（Link identification number，LIN）法[4]是一种构件的唯一数值链路标识码，此标识码可用来检测机构。然而，该方法仅适用于不超过10 个构件的运动链。

总体来说，机械结构设计迫切需要一种简单，高效和可靠的拓扑对称性识别方法。然而一方面，针对拓扑对称性的研究较少，它们大都为同构性检测方法的附加产品。另一方面，现存的对称性检测方法大都都涉及一些抽象的概念和复杂的中间参数比较，且随着杆副数量增大，一些方法的效率和有效性会大大降低，很难兼顾简便性和可靠性。因此，本文基于连杆邻接矩阵提出了一种新的拓扑对称性识别方法，即是通过运算获得一种拓扑对称性识别码。它是运动链构件的一个不变量，不随着构件标号的改变而改变。若两构件的对称性识别码相同，则它们是同构的，否则是非同构的。此方法简单、高效且整个判定过程在计算机上极易实现。

1 运动链的描述

1.1 运动链的拓扑图描述

对于单铰运动链来说，将其杆件表示为顶点，运动副表示为实线便转化成了其对应的运动链拓扑图，例如瓦特链及其对应的拓扑如图1 所示。

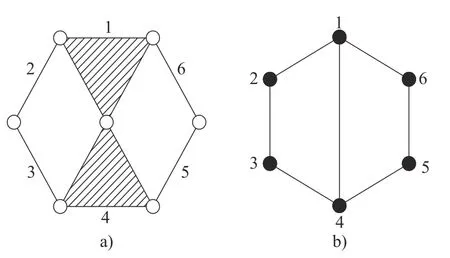
图1 瓦特链及其拓扑图

在复铰运动链中，若将复铰等效为一构件，并用空心圆表示便得到了其对应的双色拓扑图[15]，如图2所示。

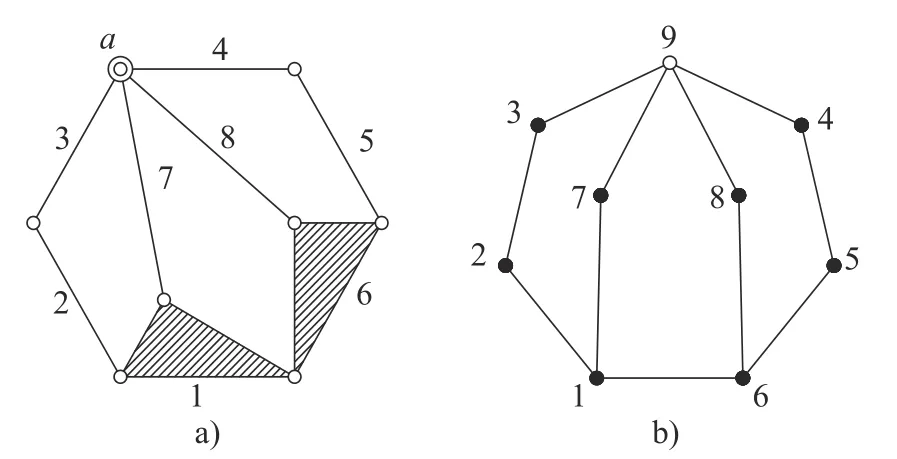
图2 一种复铰运动链及其拓扑图

基于上述复铰表达，对于行星轮系来说，只需将齿轮副表示为虚线用于区分单铰的实线便可得其对应的拓扑图[16]，如图3 所示的辛普森行星轮系及其拓扑图。

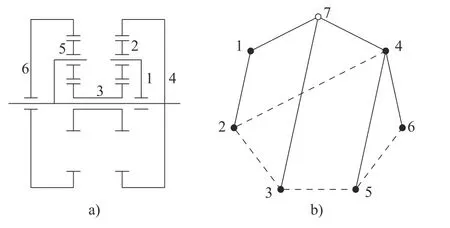
图3 辛普森行星轮系及其拓扑图

1.2 运动链的矩阵描述

本节将介绍运动链的两种矩阵描述，即连杆邻接矩阵A（Adjacency matrix）和连杆汉明矩阵H（Hamming matrix）。运动链拓扑图的连杆邻接矩阵A是其最基础的矩阵，大多数识别方法都以它为已知量或输入量，其元素aij取值为

式中：i和j为连杆标号或顶点标号，i和j为从1 到n的整数，n为运动链的连杆总数；aij的不同取值代表了不同的运动副类型。

连杆邻接矩阵的每一行代表了该标号的连杆是否与其他标号的连杆直接连接。图1 所示的瓦特链连杆邻接矩阵为

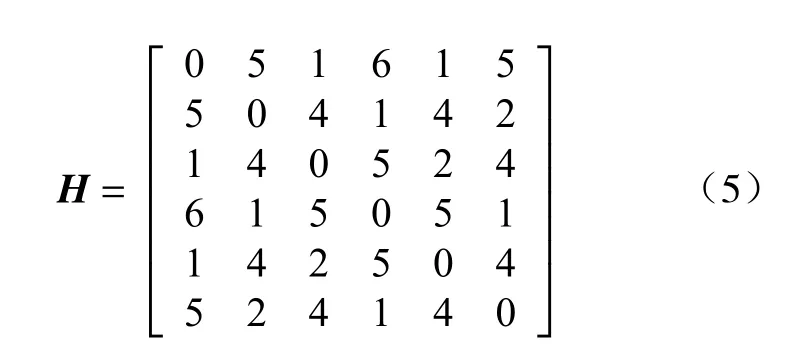
20 世纪90 年代，数字通信领域的汉明技术被引入到机械领域，并诞生出了汉明矩阵H[17]，近年来被推广到包含移动副的运动链同构识别之中[18]。它的元素hij表示连杆i和连杆j各自连接关系的不同程度。以连杆邻接矩阵为已知，hij定义为连杆邻接矩阵的第i行和第j行所有列中不同元素的总和，即：

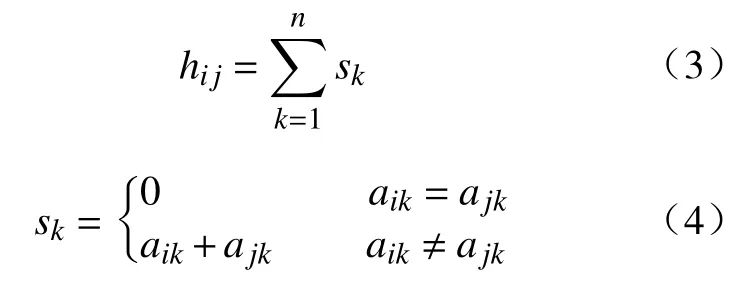
例如，对于上述瓦特链连杆邻接矩阵中的第1 行和第2 行来说，其第1、2、3、4、6 列的元素都不同，故h12=1+1+1+1+1=5。同理可得图1 的汉明矩阵，即

2 识别码的获得流程与对称性识别

2.1 识别码的获得流程

本文的拓扑对称性识别码TSRC（Topological symmetry recognition code）获得流程如图4 的阶段1 和阶段2 所示。

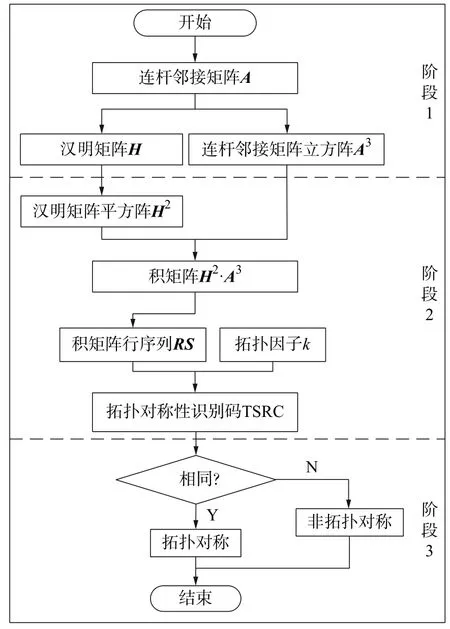
图4 构件拓扑对称性识别流程

阶段1 为从连杆邻接矩阵中导出本方法的初始量（初始矩阵），阶段2 为获得拓扑对称性识别码的运算过程，这个两阶段可细分为以下7 个步骤。

步骤1 由式（1）写出运动链或是运动链拓扑图的连杆邻接矩阵A，并将其作为本方法的输入量。

理论上，连杆邻接矩阵与运动链拓扑图是一一对应关系，它包含了拓扑图中所有的拓扑信息。因此，绝大多数的方法都以此为输入量。但连杆邻接矩阵的元素并不能作为判定方法的最终量，因其主要只表达了行列号所对应的杆件是否直接连接，而实际上两杆的关系远不止如此。要准确地描述两杆的相互关系还需将其放入整个拓扑图中考虑。于是不同的方法从连杆邻接矩阵中提取了不同的特征信息，这些特征信息的差异导致了识别能力的高低。此外，事实证明使用简单单一信息量的方法都已经出现反例[13-14]。因此为获得较高的识别能力，本文从连杆邻接矩阵中提取了多种不同的信息量作为初始量以形成TSRC，见步骤2 与步骤3。

步骤2 计算连杆邻接矩阵的3 次方阵A3，图1的A3表达式为

在连杆邻接矩阵A的m次方阵中，其元素（aij）m的几何意义为顶点i与顶点j之间距离为m条边的路径数目[17]，如图1 中A3的元素（a12）3表示连杆1 与连杆2 之间存在5 条距离为3 的路径，即为（1-2-1-2），（1-2-3-2），（1-4-1-2），（1-4-3-2），（1-6-1-2）。高次邻接矩阵揭示了拓扑图中连杆之间更宽泛的连接关系。因其参与决定元素值的顶点更多，比邻接矩阵元素更能代表一个顶点的周边环境信息，故它被选作本方法的初始量之一。此外，此处取m为3 的主要目的是为了兼顾信息量与计算量。m越大会导致计算量越大，但m次矩阵中所包含的信息量并不会随着m的增加而显著增加。

步骤3 由式（3）和式（4）的连杆邻接矩阵中导出汉明矩阵H。

因以高次邻接矩阵为基础的判定方法在某些情况下已经失效，这证明其信息量并不足以判定某些实例的拓扑对称性。因此，本方法引入了汉明矩阵作为第二初始量。它揭示了拓扑图中杆与杆之间总体连接关系的不同，其有异于连杆邻接矩阵。

步骤4 计算汉明矩阵的平方阵H2。

由于以汉明矩阵为判定依据的一阶汉明连杆邻接串在10 杆链中已经失效[14]，证明直接利用一阶汉明矩阵元素作为最终量的方法也有其适用范围。于是本文将汉明矩阵平方，放大了拓扑图中更多的细节特征，这将有助于提高识别方法的识别能力。

步骤5 求积矩阵H2·A3，图1 的积矩阵为

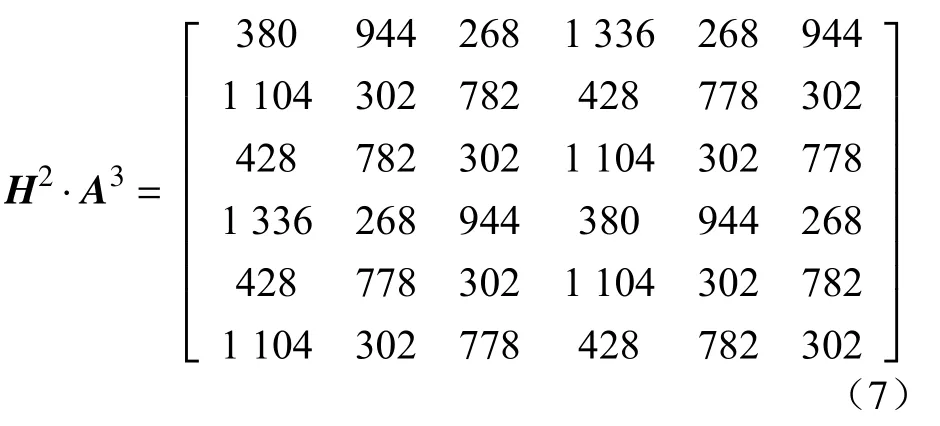
由步骤2～ 步骤4 已获得包含两种不同信息量的矩阵，本文采用将其相乘的方式获得一个全新的矩阵。若两矩阵有一方不同，则将导致乘积不同，从而获得不同的判定结果。

步骤6 将积矩阵H2·A3各行中的元素按降序排列得积矩阵行序列RS（Sequence of row），图1的积矩阵行序列RS 为

对元素排序的目的是消除因元素顺序不同而产生的不同识别码TSRC 和进一步导致的误判。如积矩阵第二行与第三行的元素分别为1 104，302，782，428，778，302 与428，782，302，1 104，302，778，显然它们元素组成相同，仅是元素位置不同。若不对它们排序而直接进行后续运算，则前者识别码为11 468，后者为13 492。这说明顶点2 与顶点3 不是拓扑对称关系，但这与由图1 中得出的结论是相互矛盾的，即为一错误结论。

步骤7 将上述行序列RS 中的元素rs乘以相应的拓扑因子k，并将所得的乘积求和以获得拓扑图的拓扑对称性识别码TSRC，即

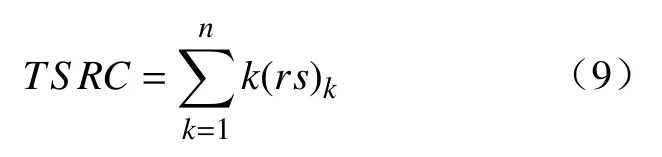
式中拓扑因子k定义为从1 到n的整数。

定义拓扑因子并乘以RS 是避免在元素组成不同而和相同的情况下产生相同的TSRC。如两RS分别为[1 2 3]和[1 1 4]，前者的TSRC 为14，后者为15。若无拓扑因子，则两者的TSRC 和都为6。图1 各构件的拓扑对称性识别码TSRC 如表1 所示。

表1 图1 各构件的TSRC 值

2.2 顶点的拓扑对称性识别

顶点的拓扑对称性是指同一拓扑图中顶点间的等效性。若将某一运动链拓扑图的顶点分别作特殊标记后，获得的新运动链拓扑图为同构[19]，那么这些顶点即为拓扑对称性顶点。如图1 中瓦特链的顶点1 与顶点4 被标记为机架，见图5。显然图5a）与图5b）为同构关系，这意味着顶点1 与4 拓扑对称。

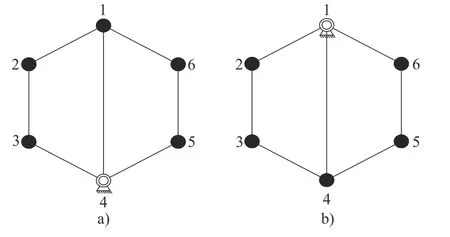
图5 瓦特链形成的两种同构机构

因拓扑图顶点的标号是任意的，所以同一拓扑图的顶点标号共有n!种。考虑到图的几何意义，顶点之间的相互位置和连接方式等结构信息在拓扑图中是恒定不变的[13]。故由图的结构信息并通过一系列数学方法所衍生得的TSRC 是顶点的一个数学不变量。所谓“不变量”是指TSRC 的值与拓扑图中顶点标号的顺序无关，顶点编码顺序发生变化不会改其TSRC。因此TSRC 可以作为拓扑对称性的判定依据。若已知两顶点是拓扑对称的，那么它们的识别码TSRC 应相等，反之亦然。其次，如果两构件是非拓扑对称的，则它们的TSRC 应为不相等。

基于上述结论，从表1 可知顶点1 与4 的TSRC相等，顶点2、3、5、6 的TSRC 也相等，这表明顶点2、3、5、6 也互为为拓扑对称。

3 判定实例与对比分析

3.1 单铰运动链

单铰运动链取自文献[14]判定失效的两实例，如图6 所示。

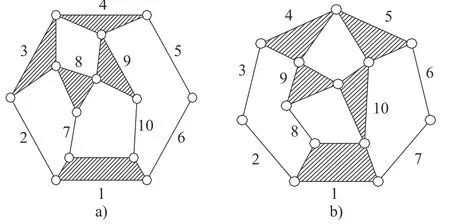
图6 单铰运动链实例[14]

该方法判定图6a）的10 杆运动链共有7 组拓扑对称性构件，即（1）（2，7，10）（3，9）（4）（5）（6）（8）；图6b）共有9 组拓扑对称性构件，即（1）（2，7）（3）（4）（5）（6）（8）（9）（10）。后图6a）被更正为8 组对称性构件，即（1）（2，10）（3，9）（4）（5）（6）（7）（8）；图6b）被更正为没有拓扑对称性构件。

由2.1 节可得出图6 各构件的拓扑对称性识别码TSRC，如表2 和表3 所示。

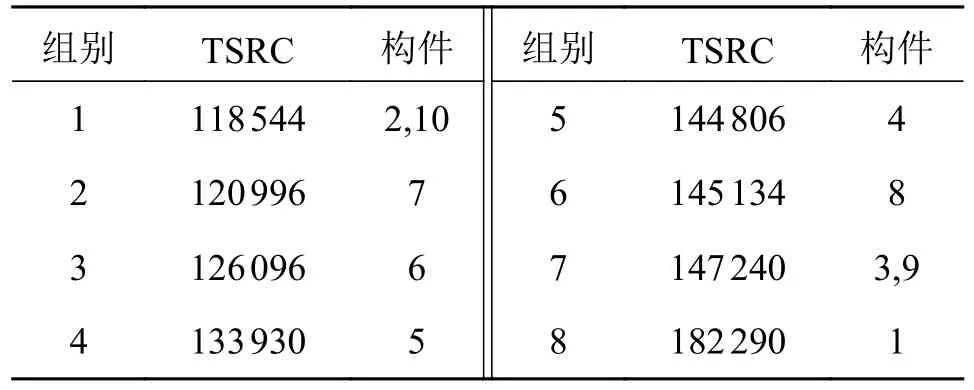
表2 图6a）各构件的TSRC 值

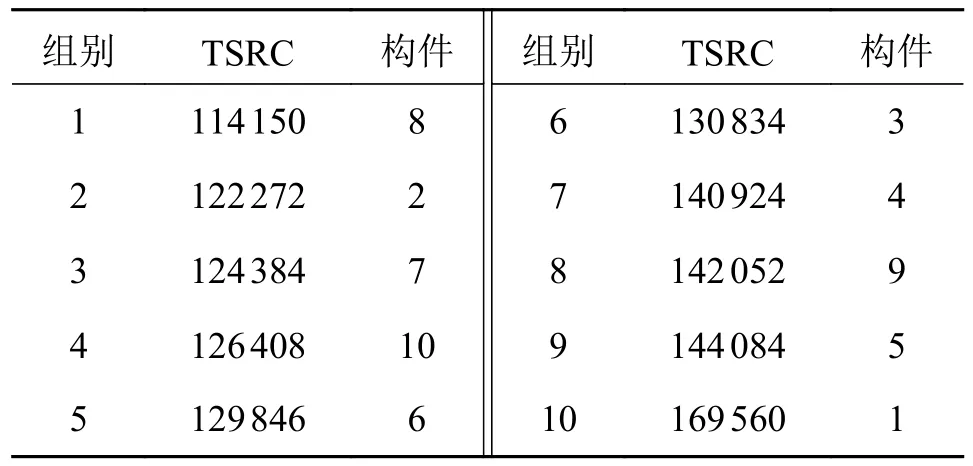
表3 图6b）各构件的TSRC 值

由表2 和表3 可知：图6a）实例中，共存在2 组TSRC 值相等的构件，即（2，10）（3，9），这意味着它们为拓扑对称性构件组（拓扑对称性构件组是指处于同一组内的各构件互为拓扑对称）；图6b）中构件的TSRC 互不相等，即顶点间互不拓扑对称。这与文献[14]更正后的正确结论一致。基于文献[14]，复现出的图6a）的汉明矩阵及其连杆一阶汉明串为

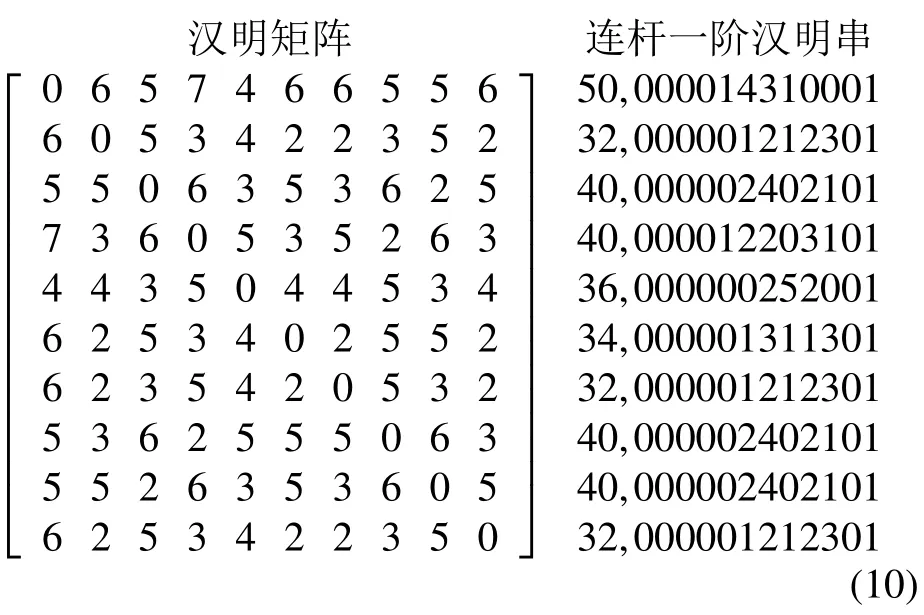
连杆一阶汉明串由两部分组成，第一部分为汉明矩阵对应的行和，第二部分为汉明矩阵对应行的元素组成情况。由上可知图6a）中存在两组相等的连杆一阶汉明串，即（2，7，10）与（3，8，9），这意味着同一组内的构件连接关系相同，但事实上从图中可以看出构件8 与构件3、9 的连接关系并不相同，构件3、9 都与公共构件4 相邻接。最终，前期未能正确区分出构件3、8、9 的连杆一阶汉明串导致了连杆邻接串（见表4）错误地识别出构件2、7、10 为拓扑对称。由上可见汉明矩阵只表现出了连杆间的总体连接特性（构件3、8、9 都与1 二副杆，2 三幅杆相邻接），而细节特征（构件8 不与构件4 相邻接）在一定程度上已被忽略。

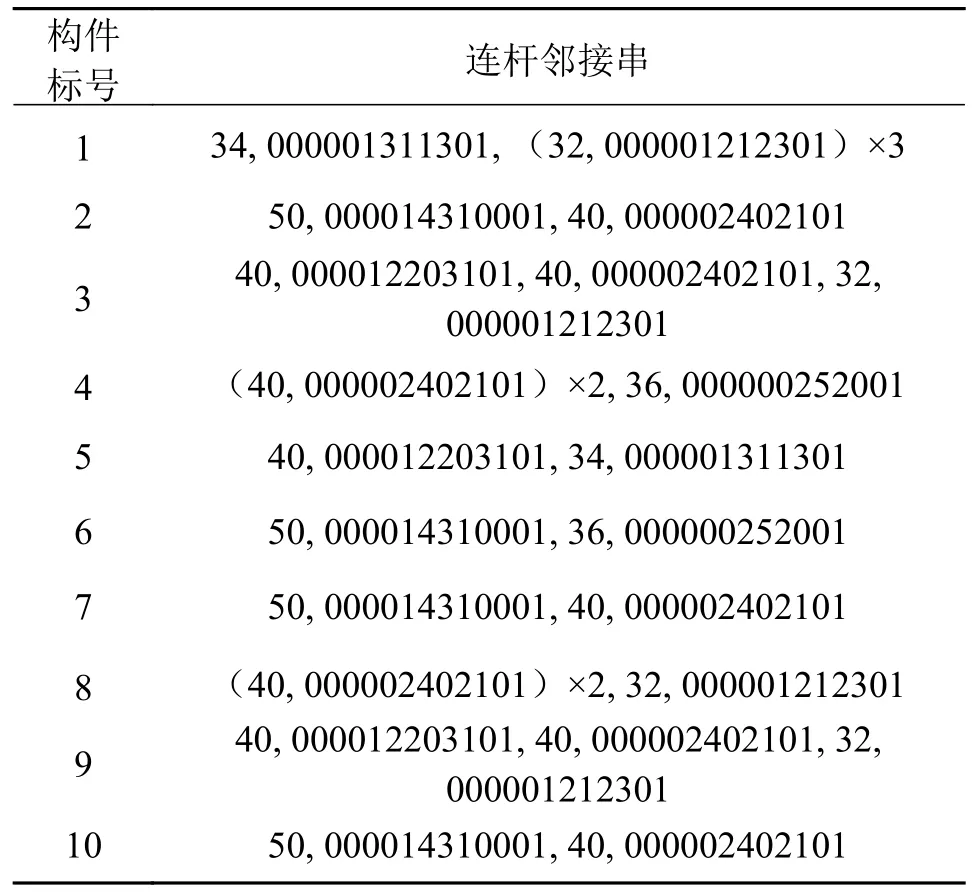
表4 图6a）各构件的连杆邻接串

总的来说，文献[14]是一种仅以汉明矩阵为依据的拓扑对称性判定方法。尽管它简单，效率高，但它却存在有效性低的严重问题，毕竟有效性才是对于一种方法最本质的要求。后来，虽然经过改进得到的2 阶连杆邻接串成功区分了该反例，但这也加大了计算量。相反，本文中的方法包含了更多的拓扑信息，这是成功区分这两对反例的关键。更重要的是本方法同样简洁高效，并且对比TSRC 比对比冗长的连杆邻接串更加容易。

3.2 复铰运动链

复铰运动链取自文献[13]中判定失效的实例。该方法判定图7a）顶点9 和顶点10 是拓扑对称的，图7b）中顶点没有拓扑对称关系。而事实上由拓扑图特性可知图7a）没有拓扑对称关系，图7b）中存在5 组拓扑对称性顶点，即（1，3）（2）（4，8，9，10）（5，7）（6）。

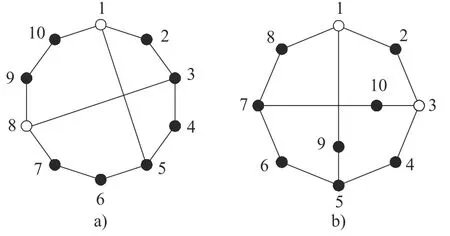
图7 复铰运动链实例

图7 各顶点的拓扑对称性识别码TSRC 分别列于表5 与表6 中。

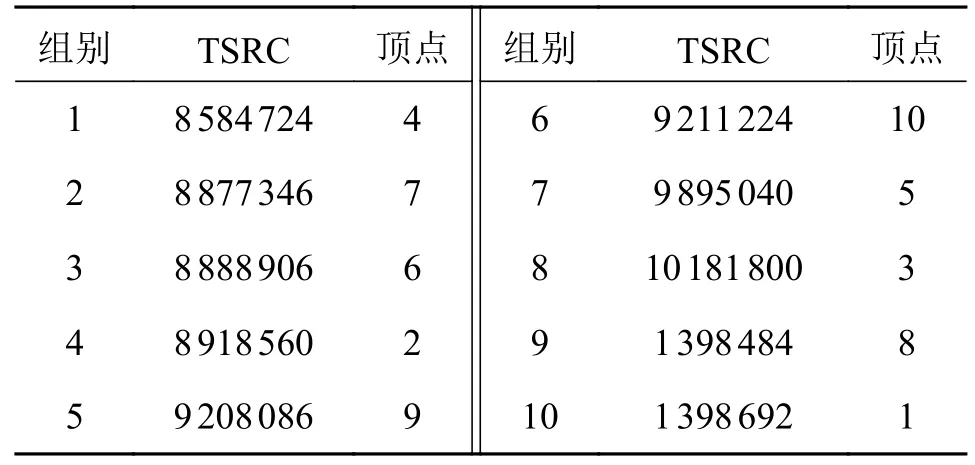
表5 图7a）各顶点的TSRC 值

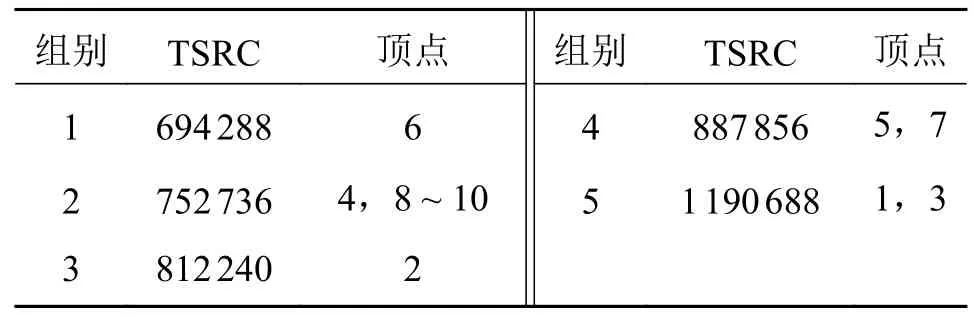
表6 图7b）各顶点的TSRC 值

由表5 和表6 可知：图7a）中顶点的TSRC 互不相等，即顶点互不拓扑对称；图7b）存在3 组TSRC 相等的顶点，即（4，8，9，10）（5，7）（1，3）为拓扑对称性顶点组。这与由拓扑图特性得出的结论一致。

由文献[13]复现出图7a）的CPVS值，见表7。顶点9 和10 的CPVS 相等，即为文献指出的潜在相似性（对称性）顶点。最终根据潜在相似性顶点和其能形成的所有可能的排列组合构建判定矩阵以排除实际顶点中有相等的CPVS 却不对称的情况，但在上述例子中这种排除效果似乎并不明显以致得出顶点9 和顶点10 拓扑对称的错误结论。

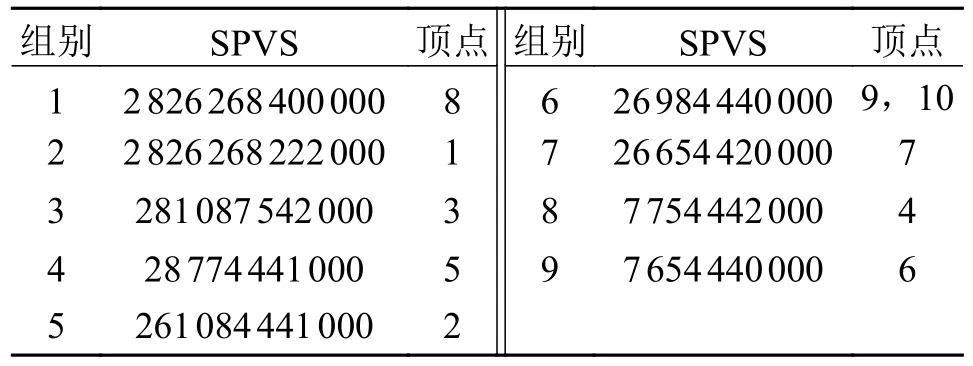
表7 图7a）各顶点的CPVS 值

总的来说，此方法[13]对具有较少构件的运动链非常有效。但当构件数或潜在相似顶点数增加时，排列组合的所有可能将大大增加，判定的工作量也将显著增加。此外，判定过程是矩阵与矩阵的比较，这比本文中数字与数字的比较更加复杂。另一方面，通过比较和排序得到的这些潜在相似性顶点也可能是非相似顶点，这意味着CPVS 的筛选能力还有待提高。更重要的是该方法也存在有效性不足的问题。然而对于本方法来说，相同的TSRC 即代表相似性，并且不需要矩阵元素的后续排列和组合，这使得本方法更加简洁高效。

3.3 行星轮系

行星轮系的实例来自于参考文献[13]，如图8所示。图8a）包含1 个复合铰链，4 个齿轮副；图8b）仅包含4 个齿轮副。由文献知图8 存在4 组拓扑对称性顶点，（1）（2，4）（3，5）（6，7）；图8b）不存在拓扑对称性顶点。

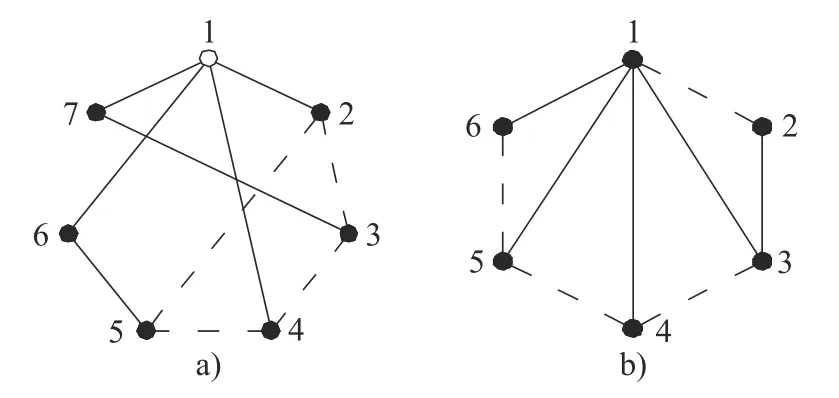
图8 行星轮系实例

上述实例各顶点的拓扑对称性识别码TSRC 列于表8 和表9 中。

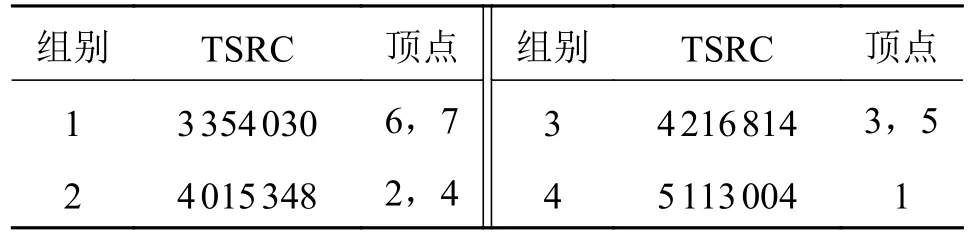
表8 图8a）各顶点的TSRC 值

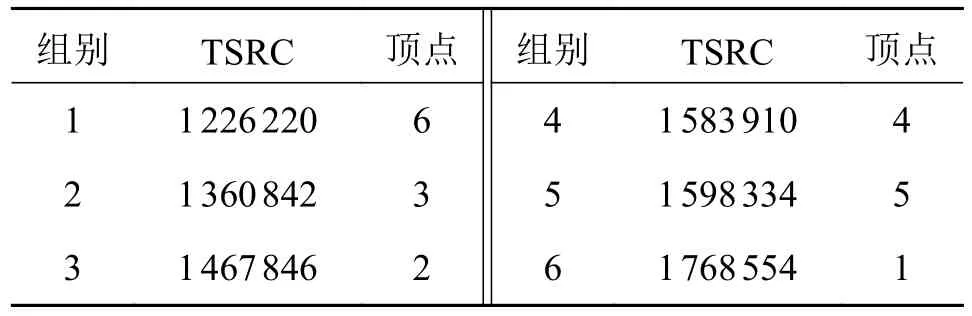
表9 图8b）各顶点的TSRC 值

由表8、表9 可知，图8a）中存在3 组TSRC 值相等的顶点，即（6，7）（2，4）（3，5），它们为拓扑对称性顶点组；图8b）中顶点的TSRC 互不相等，即顶点互不拓扑对称，此结果与文献[13]一致。

4 结论

1）本方法创造性地对汉明矩阵进行平方运算以获得运动链的更多细节信息，并将汉明矩阵的平方阵与邻接矩阵的立方阵相乘获得了一个全新的包含大量拓扑特征的积矩阵。并定义了拓扑因子，将拓扑因子与积矩阵行序列的乘积求和得到运动链构件的不变量，即运动链拓扑对称性识别码TSRC。

2）本方法逻辑简单易理解，开发本方法的计算机程序非常容易，即使对于仅有编程基础的人员来说也是如此。通过计算机程序，只需输入连杆邻接矩阵即可实现自动识别，过程简单，高效，准确。

3）对于其他方法失效的实例，本方法仍旧能够成功识别。方法的有效性经过了大量的实例验证，其中包括全部8 杆、10 杆1 自由度运动链，9 杆2 自由度运动链，含2 个复铰的8 杆1 自由度运动链，6 杆1 自由度齿轮链。但因篇幅限制，并未详述。

4）本方法易推广到其他类型运动链的拓扑对称性识别中，如含移动副和凸轮副的运动链等，只需简单修改连杆邻接矩阵形式即可。然而，本方法目前只在平面运动链中做了大量的验证，对于空间运动链的拓扑对称性，尚需更深入的研究。