一种PSO-NLM 权值曲线包络分析的单向阀故障诊断方法

李锶宇，黄国勇*,,2，潘震，钱恩丽，何冬

（1.昆明理工大学 信息工程与自动化学院 昆明 650500；2.昆明理工大学 民航与航空学院 昆明 650500）

矿浆管道输送是于20 世纪60 年代兴起的一种新的固体物料运输方式[1]。往复式高压隔膜泵是矿浆管道运输时提供动力的核心设备，单向阀是其核心零部件较其他部件更易发生故障。实际工况中，其故障冲击特征极易被大量背景噪声所淹没，频率成分复杂致使其故障冲击特征难以提取。

目前，对于单向阀振动信号处理方式主要依据时频域分析方法对信号分解，文献[2]利用局部均值分解（Local mean decomposition,LMD）方式分解为多个分量并依据能量分布选取有效分量进行包络解调提取单向阀的故障特征。文献[3]针对单向阀早期故障特征提取问题利用微分经验模态分解（Differential empirical mode decomposition,DEMD）方式分解信号，选择与原振动信号的Kullback-Leibler 散度值较小分量进行重构；文献[4]针对强噪声污染的单向阀故障特征难以提取问题，对信号进行奇异值分解，依据相关系数筛选分量。提取原始振动信号主要信息的分解方法会造成信号局部信息失真和细节丢失[5]。在保证原始信号不丢失且能有效减少大量背景噪声影响对于单向阀故障特征频率提取，准确判断故障具有重要意义。

2005 年，Buades 等[6]首次提出的一种依据图像自身结构特性和细节进行去噪的方法—非局部均值算法。2012 年，Tracey 等[7]首次运用NLM（Non-local Mean,NLM)算法处理医学领域心电图信号，得到了较好的去噪效果。2014 年，Van等[8]首次将非局部均值和经验模态分解相结合，运用在轴承故障特征提取中并成功提取相应的故障特征频率。2016 年，张龙等[9]针对强烈背景噪声下NLM 诊断效果不理想提出权重非局部平均算法的权重包络谱诊断方法，有效提取轴承故障冲击特征。针对非局部均值算法的处理效果受参数影响较大，2019 年，唐晓红等[10]将粒子群算法引入NLM参数寻优求解，以峭度值的倒数为适应度函数，有效选取适合实际工况下轴承信号的3 个参数：搜索框半径（M），相似框半径（P），带宽参数（λ）。2020 年，万书亭等[11]针对滚动轴承早期故障信号受强背景噪声影响，将非局部均值去噪方法用于滚动轴承早期故障振动信号进行降噪预处理提高信噪比。

鉴于单向阀往复过程非平稳冲击特性，与轴承旋转机械平稳振动过程具有较大差别，且单向阀发生故障时会伴有异常的振动和噪声。将NLM 算法运用于单向阀故障振动信号处理中，实际工况下单向阀故障信号包含背景噪声较多，与故障相关的冲击特征不明显，信号稀疏性较弱。包络熵值大小能有效反映信号稀疏特性，如果信号包含故障特征信息较多，包络熵值较小，信号呈现较强的稀疏性[12]。运用粒子群优化算法，以NLM 滤波信号包络熵最小作为目标函数，寻找NLM 算法最优参数。直接利用最优参数NLM 加权运算得到的信号样本点权值分布曲线作为处理信号，包络谱分析提取频率。为大量背景噪声下单向阀故障特征频率的提取提供一种新的方法。

1 方法介绍

1.1 非局部均值算法(NLM)

假设u为无噪声真实信号，n为背景噪声信号，则实际带噪声信号y表示为

基于非局部均值降噪算法是将真实信号u从包含噪声信号n的实际信号y中通过消除噪声恢复真实信号的过程。则以去噪点t为中心的搜索区域内N(t)所包含的所有点的权重平均值K(t)可表示为

式中Z(t)为归一化因子。

式中w(t,s)表示权重。

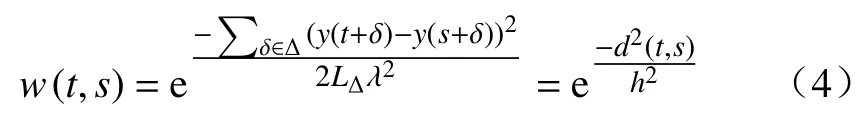
式中：权重w(t,s)值的大小取决于t和s两点领域块之间欧式距离的平方和d2(t,s)，参数h为带宽参数控制指数函数即w(t,s)的衰减速度。权重w(t,s)取值满足如下两个条件：

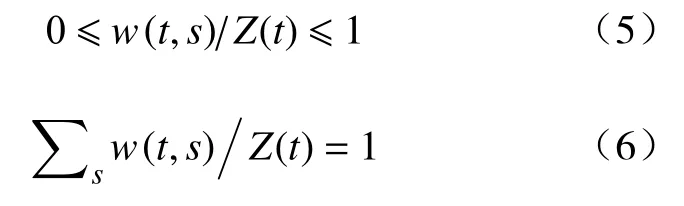
1.2 权值曲线包络分析

NLM 算法依据各样本点邻域之间的局部结构相似性提取信号中存在的周期性冲击特性，通过对相似样本点平均化来减少噪声。权重w取值取决于以去噪点为中心的相似区域与其他点为中心的相似区域之间相似度。两个相似区域相似度越大则权值贡献越大，即权重运算后该点w取值越大。

权值贡献计算思路如图1 所示，图中t为去噪点，N(t)表示以去噪点t为中心半径为M的搜索范围。n(s)、n(t)、n(v)分别表示以点s、t、v为中心半径为P的相似区域。其中，相较于n(v)与n(t)的相似度，n(s)与n(t)的相似度明显较大。则点s的权值贡献越大。对于往复运动的单向阀采集的振动信号，冲击特征是稀疏成分，而信号中剩余信息包含大量背景噪声。冲击特征作为稀疏成分，当n(t)为冲击范围时，在搜索范围N(t)内与n(t)相似的成分较少，此时权值贡献较小。为避免平均化过程导致单向阀自身信号的冲击特征均值化，以加权运算后信号各样本点的权值分布曲线作为处理信号，进行希尔伯特包络谱分析提取单向阀故障特征频率。

图1 NLM 参数关系

1.3 PSO-NLM 算法

影响NLM 算法的3 个决定性参数：搜索框半径M，相似框半径P，以及带宽参数h。参数M决定搜索区域的大小，M值越大，则搜索区域内的相似区域越多，NLM 滤波效果越好，但其耗时长而影响计算效率。P决定相似区域的大小，P值过大会导致信号的部分关键信息丢失，过小会造成相似块区域增多，致使相似块信息不具有代表性。h控制指数函数即w(t,s)的衰减速度。h过小，容易引起噪声波动，造成相似块之间平均化不充分；h过大，滤波信号过于平滑，细节丢失严重，导致高失真率。

NLM 算法参数组合是影响NLM 算法处理信号的关键所在。粒子群算法[13]具有较好的全局寻优特性，本文利用其对NLM 算法3 个参数（M，P，h）进行优化，筛选出NLM 最优参数组合。

粒子群优化算法中，假设在D维空间中存在N个粒子组成的种群，每个粒子在搜索过程中依据个体局部极值和种群全局极值不断调整自身的速度和位置，表述为：

式中：C1，C2为加速度控制参数；w为惯性权重；η是取值在[0,1]之间的随机数；k为迭代次数；分别为第i个粒子在第k，k+1 次迭代时的速度；分别为第i个粒子在第k，k+1 次迭代时的位置；分别表示第i个粒子在第k次迭代时的个体局部极值和种群全局极值。

目标函数的选择直接影响粒子群算法寻优结果的准确性。Shannon 熵是一种很好的评价信号稀疏特性的标准，熵值的大小反映了概率分布的均匀性，最不确定的概率分布（等概率分布）具有最大的熵值[14]。包络熵是将信号解调运算后得到的包络信号处理成一个概率分布序列pj，包络熵值能反应原始信号的稀疏特性[12]。零均值信号x(j)(j=1,2,3,···,N)的包络熵Ep可表示为：

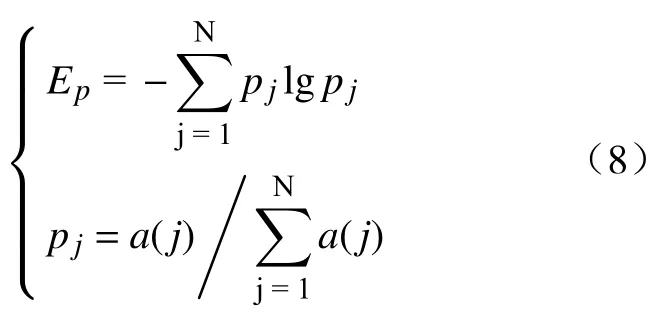
式中：pj是a(j)的归一化形式；a(j)是信号x(j)经Hilbert解调后得到的包络信号。

对于包含大量背景噪声的单向阀故障信号而言，其信号稀疏性较弱。NLM 滤波后的信号包络熵值越小，说明此时信号中出现有规律性的冲击特征越明显，信号稀疏性较强。本文选取包络熵作为粒子群算法的适应度函数。则NLM 算法的M，P，h的优化步骤如下：

1）种群初始化。设定各项参数如初始位置、初始速度、迭代次数、种群规模、NLM 参数M，P，h范围等。

2）设置目标函数。依据NLM 滤波信号的包络熵值最小作为目标函数即适应度函数，计算第一代个体极值和全局极值。

3）迭代寻优。依据公式（7）自动更新种群的粒子位置和速度，并计算新粒子适应度值，循环迭代获得最优个体局部极值和种群全局极值。

4）输出NLM 最优参数组合，当进化代数达到最大迭代次数后停止搜索，将得到NLM 最优参数M，P，h。

2 诊断流程

对于大量背景噪声信号下单向阀故障特征难以提取的问题，文中选用NLM 方法对信号进行处理，运用粒子群算法搜寻NLM 算法最佳参数组合。对NLM 权值分布曲线作包络谱，则PSO-NLM 权值分布曲线包络分析具体实现步骤如图2 所示。

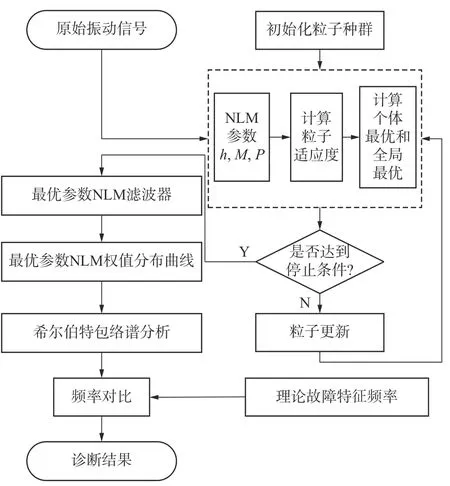
图2 PSO-NLM 权重包络诊断方法

1）设定粒子群算法各参数并搜寻NLM 算法参数M、P、h。种群规模，学习因子和权重因子主要依据参考文献[10]进行NLM 参数的设定，其中最大迭代次数G，依据对象进行设定。粒子群算法设定的各项参数如表1 所示。

表1 粒子群算法参数设定

2）以NLM 滤波后信号包络熵作为目标函数来搜寻NLM 最优参数（M，P，h），为避免NLM 滤波过程冲击特征均值化的影响，以NLM 权值分布曲线作为处理信号。

3）对NLM 权值分布曲线作希尔伯特包络谱，对于提取到的频率与理论特征频率比对来判断故障。

3 单向阀故障诊断

3.1 试验方法及单向阀机理分析

本试验数据来源于云南大红山铁精矿输送管道，单向阀作为核心设备高压隔膜泵的关键零部件更容易发生故障。图3 为本文采集信号所涉及的管道输送的高压隔膜泵简图和故障单向阀实物图。

图3 高压隔膜泵及故障单向阀实物图

本试验数据是对采集到的单向阀故障振动信号进行分析判断，单向阀是由阀体，阀芯和弹簧组成的锥式结构，其中阀芯和弹簧组合可以看作1 个2 阶振荡环节，频率计算公式[15]为

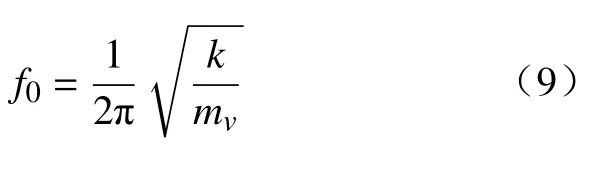
式中:k为弹簧刚度；mv为阀芯弹簧系统的等效质量。根据泵的柱塞运动情况，将弹簧刚度设为

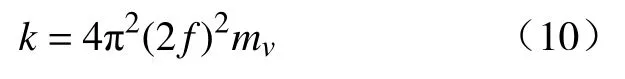
式中f为高压隔膜泵正常运行的频率。弹簧-阀芯系统的频率f0=2f，即1～1.034 Hz。当泵单向阀出现故障时，其特征频率包含单向阀的频率及泵的固有频率和其倍频特征频率。

3.2 试验分析

文中所用数据为单向阀发生故障时所采集的振动信号，其采集频率为2 560 Hz，采样数据取10 240点，且通过现场得知高压隔膜泵的正常运行时频率为0.5～ 0.517 Hz。

采集的单向阀故障信号，其时域波形和希尔伯特包络谱如图4 与图5 所示。单向阀原始故障信号受大量背景噪声的影响，如果直接对信号进行包络谱分析无法直接提取到故障特征。干扰频率较多，且频率主要分布在0～ 200 Hz。

图4 原始信号时域波形

图5 原始信号希尔伯特包络谱

为有效较少噪声干扰，尽可能保留原始信息，有效提取单向阀故障特征。将采集到的单向阀信号运用文中方法进行处理，运用粒子群算法对NLM 参数进行参数选择，以NLM 滤波信号包络熵值最小作为目标函数。PSO 收敛曲线如图6 所示，可以看到以包络熵为目标函数的包络熵值随着迭代次数的递增而不断减小，并趋于稳定。此时参数取值：M=8，P=4，h=1.843 4。

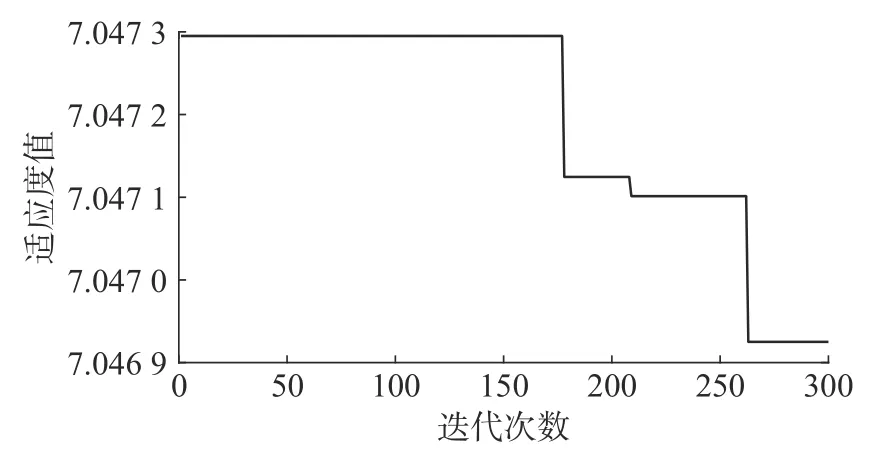
图6 PSO 收敛曲线

图7 为最优参数NLM 加权运算得到的信号样本点权值分布曲线，图8 为最优参数NLM 权重分布曲线的希尔伯特包络谱，对权重分布曲线进行包络谱分析有效提取到单向阀正常工作的基频相近成分0.937 5 Hz，且提取到其二倍、四倍、五倍频，同时提取到0.625 Hz 及其多倍频特征等突变特征，这些频率特征成为单向阀故障信号的主导频率，表明此时单向阀必定发生故障。文中方法有效避免NLM 均值化导致冲击特征弱化的问题，且从权重角度对冲击特征进行增强，包络谱幅值明显增大。

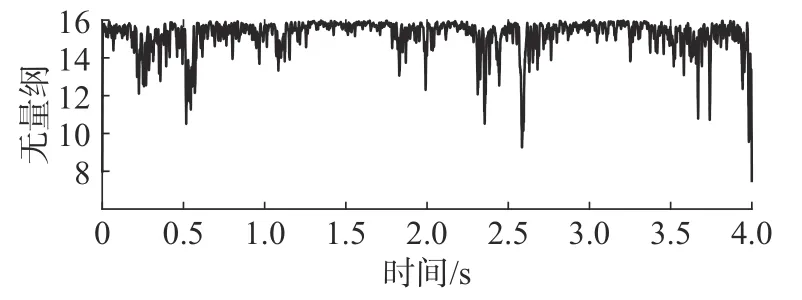
图7 最优参数NLM 权值分布曲线

图8 最优参数NLM 权值分布曲线希尔伯特包络谱

3.3 方案对比

经验非局部均值算法对数据进行处理时，参数λ的取值通过SURE 准则选择[16-17]。上述文献中根据SURE 准则确定适合本实验参数λ的取值为0.5σ，其中σ为信号的方差。计算得到单向阀故障振动信号σ=0.163 4，参数M，P多为人为经验进行选取，因此数据处理结果呈现出多样性。本文选用M=10，P=10，λ=0.081 7，h=0.266 9。

图9 为最优参数NLM 滤波后信号，图10 为最优参数NLM 滤波信号希尔伯特包络谱分析，单向阀正常工作的基频相近成分0.937 5 Hz 被表征出来且包含其二倍频成分，同时提取到0.625 Hz 的频率。但冲击特征不明显，且包络幅值较小。NLM 算法求均值导致部分冲击特征均值化而无法精准的对单向阀故障冲击特征频率进行提取。

图9 最优参数NLM 滤波信号

图10 最优参数NLM 滤波信号希尔伯特包络谱

NLM 算法自身受噪声影响较大，权值计算作为计算核心也受其影响。传统NLM 权值分布曲线如图11 所示，相比于图7，传统NLM 处理后得到的权值曲线冲击特征表征不明显。

图11 传统NLM 权值分布曲线

传统NLM 权值分布曲线希尔伯特包络谱如图12 所示，相比图8，提取到0.625 Hz，0.937 5 Hz，1.875 Hz 和3.75 Hz，部分倍频成分未能有效提取，文中方法提取到的突变特征频率更为明显。

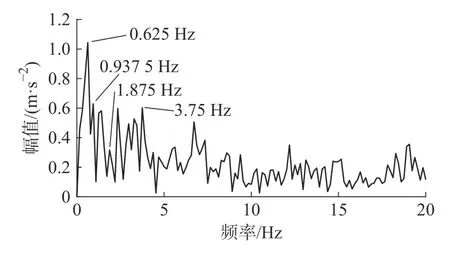
图12 传统NLM 权值分布曲线希尔伯特包络谱

4 结论

1）将NLM 算法运用在单向阀振动信号处理时，受噪声影响较大，以最优参数NLM 算法降噪后，直接包络分析滤波信号效果不理想。

2）文中方法有效避免了NLM 算法滤波过程冲击特征均值化的影响，对权值曲线进行希尔伯特包络谱分析，从权重角度增强其故障特征，有效提取大量背景噪声下故障信号的特征频率。

3）通过试验对比，文中提出的PSO-NLM 权值分布曲线包络分析方法与最优参数NLM 滤波信号包络分析方法和传统NLM 权值分布曲线包络分析方法进行对比，进一步证明文中方法的优越性。