SUV 双横臂悬架性能分析及优化设计

钱飚，金智林

（南京航空航天大学 能源与动力学院，南京 210016）

随着汽车行业的不断发展，人们对汽车平顺性、舒适性、操纵稳定性的要求也越来越高，其中起关键作用的就是汽车悬架[1]。因此，如何设计出满足用户各种需求的悬架是汽车设计过程中必须考虑的问题。

在现代悬架的开发过程中，悬架的K&C 特性始终受到密切关注，它直接反映悬架性能的好坏[2]。国外对于悬架K&C 特性的研究在20 世纪70 年代开始，研究了包括车轮定位参数随轮跳的变化，车轮受力随车轮前束角、外倾角的变化，方向盘转角对其特性的不同影响等[3-4]。随着对悬架的要求不断提高以及对悬架特性的研究逐渐深入，各种悬架的研发和应用方面取得了丰硕的成果[5-6]。

双横臂悬架由于其优异的性能在汽车上得到广泛的应用[7]。合理布置的双横臂悬架可以精确控制车轮的运动，实现侧倾中心高度和车辆质心的匹配，同时可以有效减少因为轮距的变化导致的轮胎磨损[8-9]。如何设计双横臂悬架布置方式使其满足设计要求是需要考虑的主要内容。目前主要的研究方法是采用虚拟样机技术来建立相应模型，探究采取不同布置时定位参数对平顺性和操纵稳定性的影响[10]。

虚拟样机技术是在多体动力学理论的基础上建立的一种辅助运算工具，能够极大的便利工程师对产品的运动和受力进行分析。计算机技术发展起来之前，学者更多的是根据理论分析以及工程经验来定性分析各种结构属性对悬架性能的影响，没有能力根据硬点的坐标定量分析悬架性能，计算机辅助设计为这一需求提供了可能。其中，Adams Car 是虚拟样机技术的典型代表，能够有效的简化建模的工作，提高仿真的精度和效率，极大降低设计成本，实现对建模和优化的目标要求[11]。

Zhang 等[12]建立麦弗逊悬架模型，通过Adams Insight 对不满足设计要求前轮前束角和主销内倾角进行了优化，使其满足车辆的舒适性和操纵稳定性需求。刘鹏[13]运用Adams Car 建立悬架模型，优化了电动轮驱动汽车的双横臂悬架系统运动学特性，建立了悬架的响应面模型，最后通过非归一化的优化算法NSGA 优化悬架系统，得到所求的最优解。张向东[14]在Adams Car 中建立双横臂悬架模型，对主要定位参数进行分析优化，搭建整车动力学仿真模型，对比优化前后的操纵稳定性与纵向冲击舒适性，实现了自己的优化要求。

关于悬架性能的优化设计，相关学者已经做了许多工作，但对于不同的悬架，面临的问题不同，优化参数及优化设计的方法也不尽相同。本文运用Adams Car 模块，依据已有SUV 的硬点坐标建立双横臂前悬架模型，仿真分析双横臂悬架性能；通过Adams Insight 模块优化调整相应的硬点坐标，使得相应的悬架定位参数在车轮跳动时按要求变化，提高目标SUV 双横臂悬架的性能。

1 SUV 双横臂悬架模型

本文研究目标为某SUV 车辆，针对该车存在的过度轮胎磨损问题和考虑到对车辆直线行驶稳定性以及适当不足转向的需求，对其前悬架进行相应的优化，该车具体参数如表1 所示。

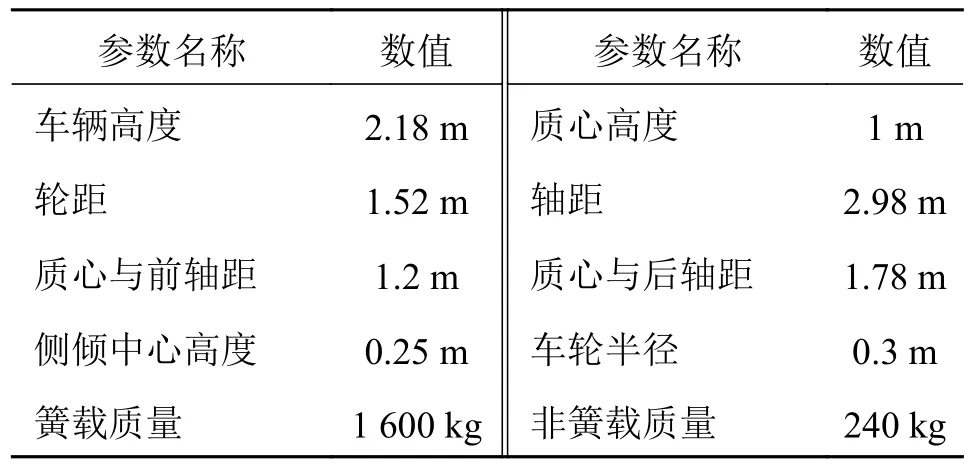
表1 SUV 车辆参数

悬架的关键点的空间坐标即常说的硬点坐标通过三坐标测量仪进行测绘，硬点坐标可以概括描述该悬架的几何形状。该SUV 双横臂悬架硬点坐标见表2。前轮的初始定位参数通过车轮定位仪测量，得到初始车轮外倾角0.1°，前束角0.1°，主销后倾角5.43°，主销内倾角10°。

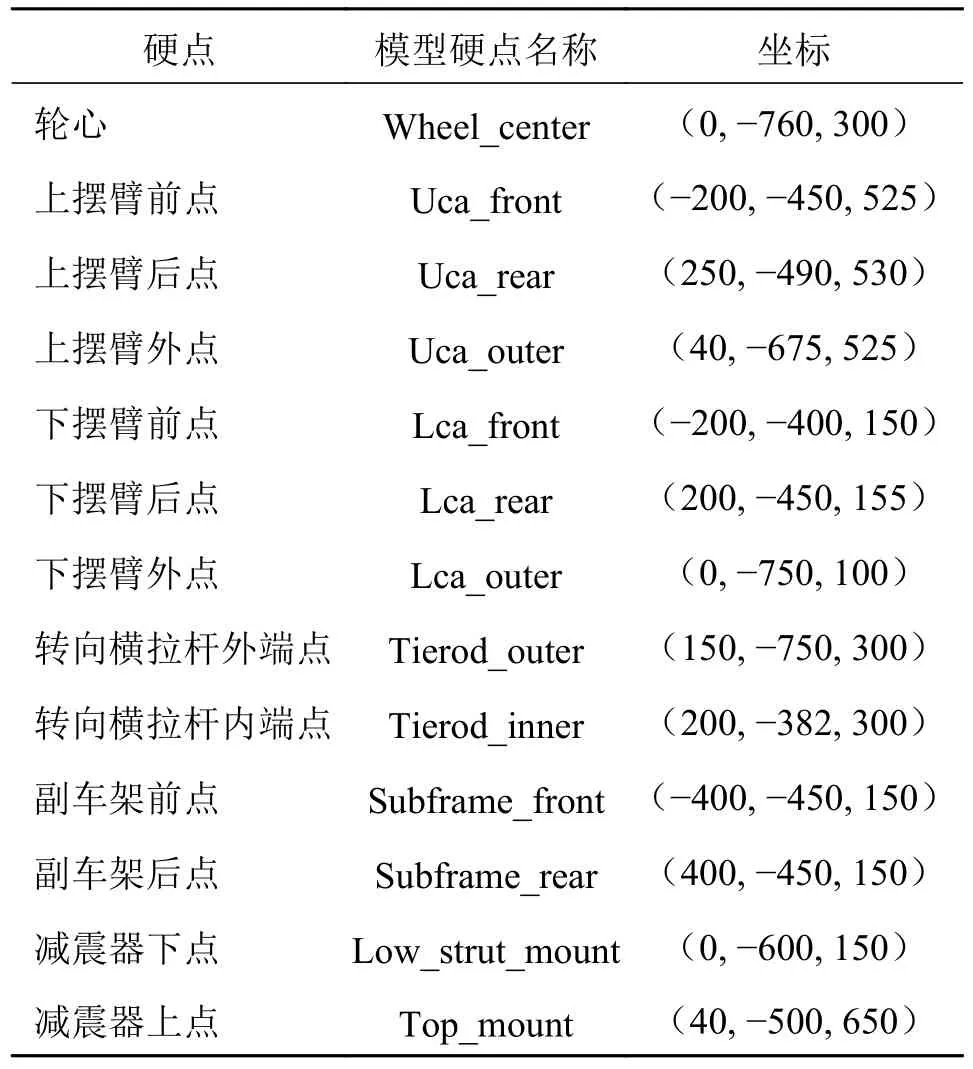
表2 双横臂悬架初始硬点坐标

双横臂悬架的主要由上横臂、下横臂、主销、转向节、转向横拉杆和减震器等组成。在Adams Car 中依据该SUV 悬架的硬点坐标，依次建立部件、几何体、连接、力元件和通讯器等，得到双横臂悬架模板。本文将双横臂悬架子系统和转向子系统集成装配，得到SUV 双横臂悬架Assembly 模型，得到仿真模型如图1 所示。

图1 双横臂前悬架模型

2 SUV 双横臂悬架性能分析

2.1 双横臂悬架仿真试验

在Adams car 中有多种仿真类型可供选择，为了研究车轮定位参数随车轮跳动的变化规律，选取最具代表性的平行轮跳（Parallel Travel）试验，试验步数设置为100，仿真的类型设置为运动学特性，轮跳设置为±50 mm。平行轮跳的参数设定如表3所示。

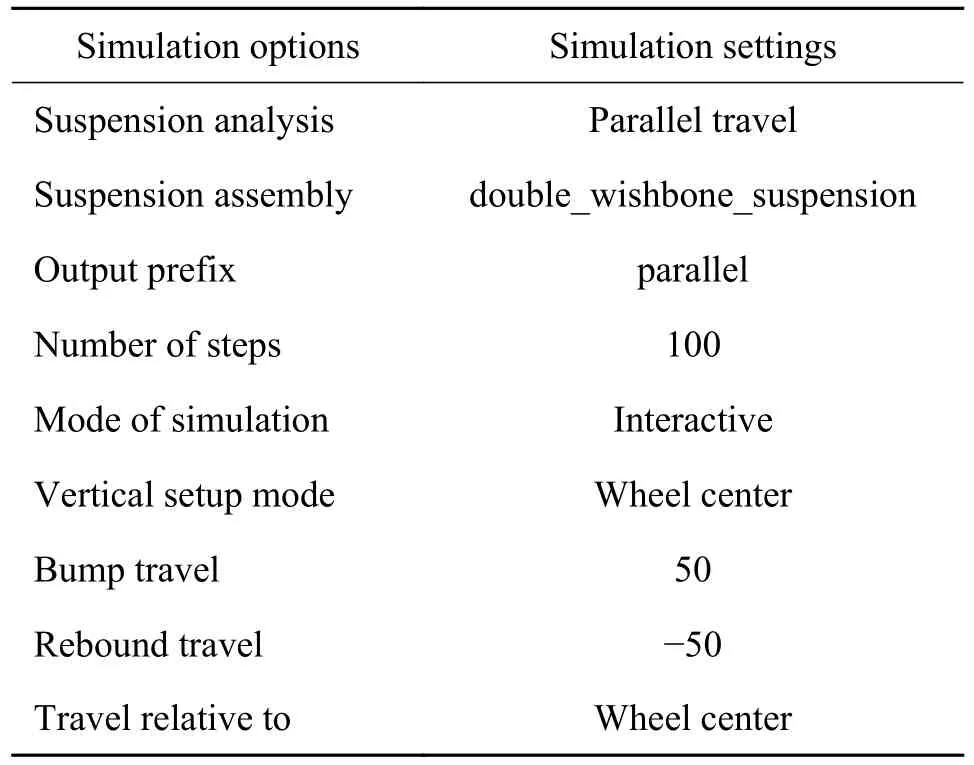
表3 平行轮跳参数设定

试验完成后，调用Animation Controls 模块观察过程是否正确，接着调用后处理模块（Postprocessor）以研究各个定位参数随轮跳的变化规律以用于分析优化。

2.2 双横臂悬架运动特性分析

对于车轮定位参数随轮跳变化情况，不同悬架有着不同的要求，参考《汽车工程手册》中对悬架特性一般值的变化范围要求[15]，结合具体悬架情况，对该双横臂悬架进行特性分析。

图2 为平行轮跳试验时车轮外倾角变化曲线。车轮上跳及回弹时引起的外倾变化对车辆直线行驶过程中的稳定性、不足转向特性以及过度转向特性的影响不可忽略。轮胎与路面接触时的外倾角存在，将会产生相应的外倾推力，外倾推力与因侧滑角的存在导致的侧向力的合力充当了车辆转向的推力。为了发挥轮胎的能力，希望轮胎总是垂直于地面，因此对地的外倾角应该控制在较小的范围内。在轮跳±50 mm 的范围内，车轮外倾角保持在较小的范围内变化，最好在-1°～ +0.5°/50 cm 上跳。该双横臂悬架的车轮外倾角变化范围在-1.25°～ 0.5°，上跳50 cm 时的变化为-1.25°，不符合要求，需要进行优化。

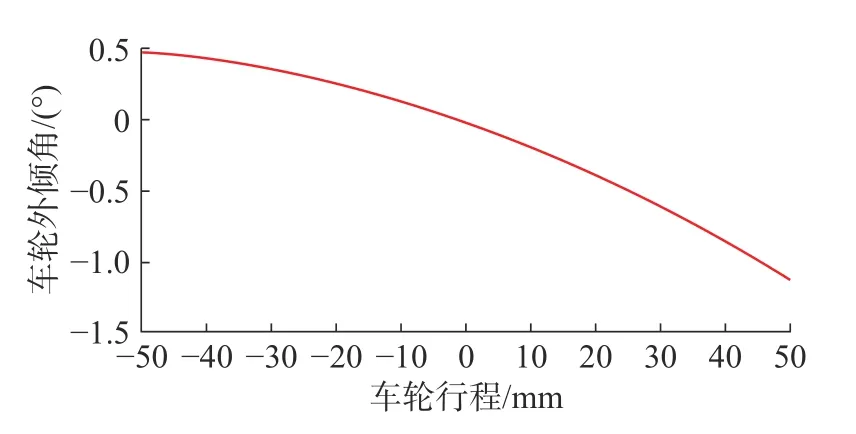
图2 平行轮跳-车轮外倾角变化曲线

图3 为平行轮跳试验时主销后倾角变化曲线。主销后倾角的存在将影响转向时的外倾变化，如果主销后倾角的预设值很大，则外倾转向轮相应外倾角会存在负的变化趋势。当存在较大的前轮主销后倾角时，前轮转向所需要的横向力需适度增大，用来抵消产生的外倾推力,此时车辆存在较弱的不足转向特性，横向加速度的阈值会提高。所以一般要求前置前驱车主销后倾角在1°～ 7°之间变化，前置后驱车的主销后倾角在3°～ 10°之间变化，所设计的双横臂悬架主销后倾角在范围5.25°～ 5.7°之间变化，满足设计要求。

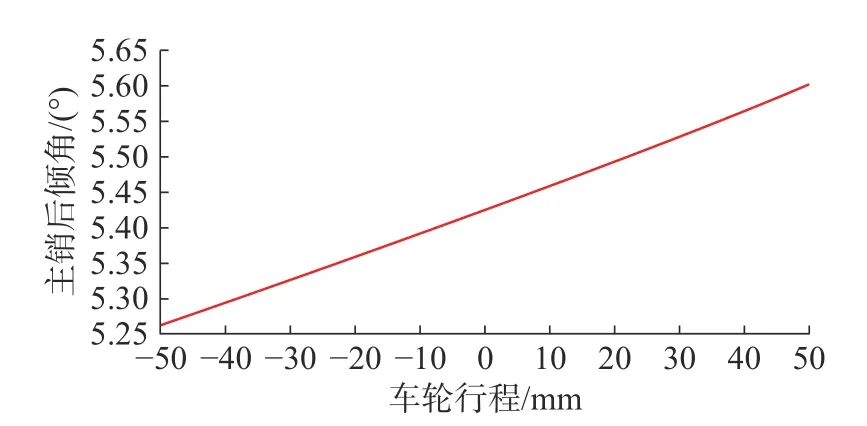
图3 平行轮跳-主销后倾角变化曲线

图4 为平行轮跳试验时车轮前束角变化曲线。车轮上跳及回弹时的引起的前束值变化对车辆直线行驶时的稳定性、不足转向特性和过度转向特性的影响不可忽略。对于前轮，要求车轮上跳时的前束值多数为0 至负前束之间变化，确保良好的直线行驶稳定性，同时确保因车载质量发生变化而引起车高变化时也能保证不足转向特性。当车轮前束值随着车辆的运动有着过大的变化时，车辆的直驶稳定性将被影响，同时增大的滚动阻力将增大轮胎磨损，影响其寿命。所以前束角的设计原则是在车轮跳动时，保持在较小的范围内变化。该双横臂悬架的前束角在平行轮跳试验的变化率为-2°/50 mm，为保证合适的不足转向特性，前束变化率应该在-1°/50 mm以内，不符合要求，应进行优化。

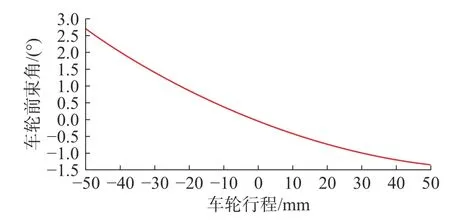
图4 平行轮跳-车轮前束角变化曲线

图5 为平行轮跳试验时主销内倾角变化曲线。合适大小的主销内倾角可以使汽车转向回正、转向操作轻便。如果主销内倾角不合适引起主销偏移距过大时，将导致较大的回正力矩引起转向盘“打手”现象。在车轮跳动时，一般取主销内倾角变化范围在5°～ 15°之间，目标悬架的主销后倾角在9.25°～ 11.5°之间变化，符合设计要求。

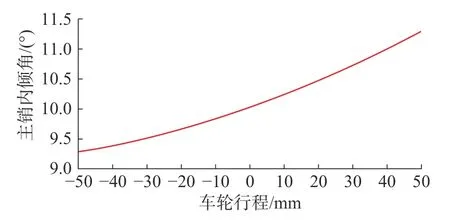
图5 平行轮跳-主销内倾角变化曲线

3 SUV 双横臂悬架优化设计

3.1 优化目标及优化变量

硬点坐标的改变将引起悬架各个部件相对位置的变化，最终导致悬架特性改变。本文选择对定位参数变化灵敏度高的硬点，在Adams/Insight 模块中进行硬点坐标优化，根据预设的定位参数目标，得到合适的硬点坐标，实现对于悬架优化设计的构想。

使用Adams/Insight 模块，对前面确定的定位参数进行优化。根据前文分析确定主要参数的变化范围约束，主要对车轮外倾角和车轮前束角进行优化，同时注意其他参数的变化。

根据参数灵敏度选取下摆臂前点（Lca_front）、下摆臂后点（Lca_rear）、下摆臂外点（Lca_outer）、转向横拉杆外端点（Tierod_outer）这4 个硬点的x、y、z这3 个方向上共12 个坐标值作为优化目标。优化过程中硬点的变化范围取-10～10。

3.2 优化方法

Adams Insight 提供了多种优化策略（Investigation Strategy）和试验设计算法（DOE design type）选择，这里根据优化需要，优化策略选择二阶响应面法，试验设计算法选择D-optimal 算法。

响应面分析法，是一种基于实验数据，利用多元二次回归方程通过拟合的方法得到因素和响应之间的映射关系，分析所得到的回归方程来寻求多变量问题的解的一种方法。

当响应值与因素之间的关系为线性时，进行一阶响应曲面拟合。

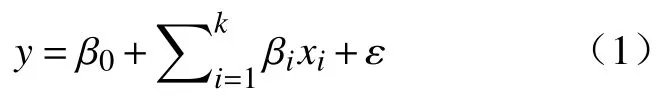
式中：βi为xi的斜率；ε为误差。

当响应值与因素之间的关系为非线性时，进行2 阶或者更高阶的响应曲面拟合，2 阶响应曲面表达式为

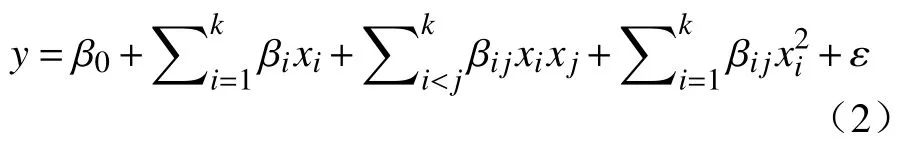
式中βij为xi与xj之间的线性交互效应或者xi的二次效应。

D-optimal 试验设计可以使得所建立的模型的渐进协方差矩阵的行列式的值最小，该理论最终可以实现减小模型参数的标准误差，最终得到更加可靠的参数估计结果。假设试验系统的回归模型为：

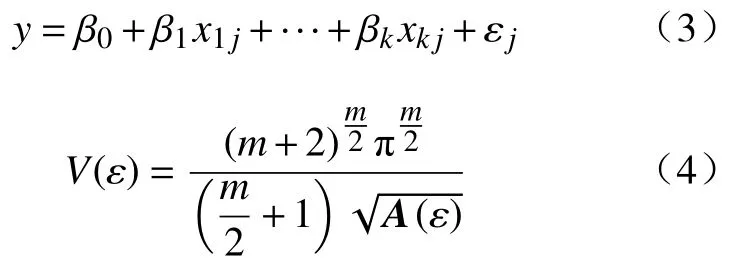
式中A(ε)为试验设计的信息矩阵，找到使得V(ε)最小的试验设计算法即为D-optimal 试验设计算法。

3.3 优化结果分析

设定所选择的试验方法后，创建优化系统的工作矩阵。在保证计算精度的前提下尽量减少计算时长，选取256 次迭代进行优化。优化完成后，从导出的web 页面分析设计变量对优化目标的影响。选取目标数值后，得到如表4 所示的优化后的硬点坐标。

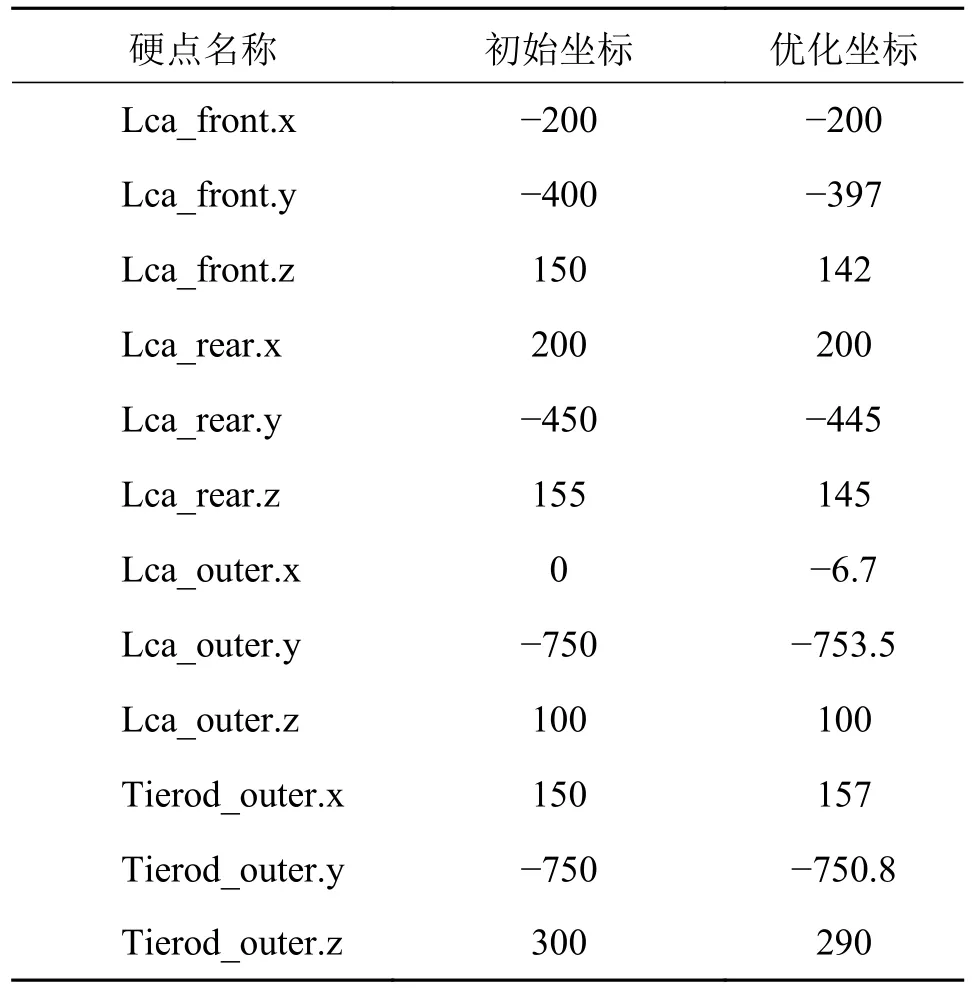
表4 优化前后硬点坐标对比

优化过后得到新的硬点坐标，在模型中修改硬点坐标后，重复前文中平行轮跳仿真，将优化前后的SUV 双横臂悬架定位参数变化进行对比分析，图中虚线表示硬点坐标优化后的仿真曲线。

图6 为优化前后车轮外倾角变化曲线。分析可知，车轮外倾角的变化范围由最开始的-1.25°～-0.5°变化到-1°～-0.25°，变化范围减少了29%，同时优化后车轮上跳50 cm 的车轮外倾角的变化范围在1°左右，满足优化要求。从综合考虑转向性能和直线行驶稳定性的观点出发，优化后的上跳及回弹时的外倾变化在要求的范围内。

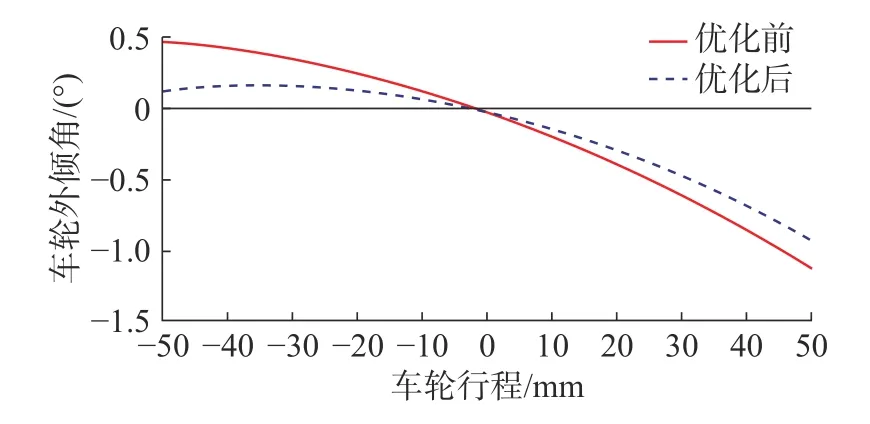
图6 优化前后车轮外倾角变化曲线

图7 为优化前后主销后倾角变化曲线。图7 表明，主销后倾角的随轮跳的平均变化范围由原先的5.4°变化到6°，优化后的数值在要求的变化范围之内，满足设计要求。主要考察主销角度在设载状态下初值设置，主销内倾与后倾的变化趋势不做硬性要求。全行程下角度变化 0.2°以内，优化后的主销后倾角变化范围更小。基础主销角度设置合理，因此优化主销角度参数也在合理范围内。

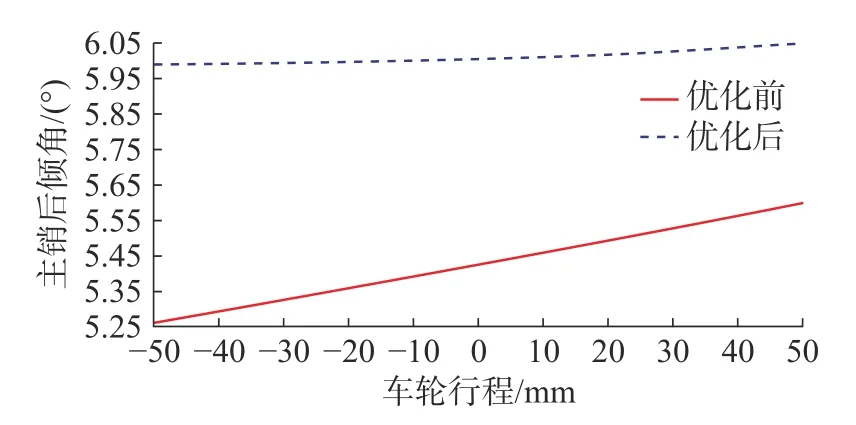
图7 优化前后主销后倾角变化曲线

图8 为优化前后车轮前束角变化曲线。通过图8 可知，优化前的前悬前束变化率为-2°/50 cm，前束变化率过大，车辆的行驶稳定性较差，轮胎磨损剧烈。优化后的前束角变化到-0.5°～ 1.5°，经优化后的前束值变化范围减小50%，前束变化率在-1°/50 mm 以内，增加了车辆行驶的直线稳定性，减少了轮胎磨损，保证了合适的不足转向特性。

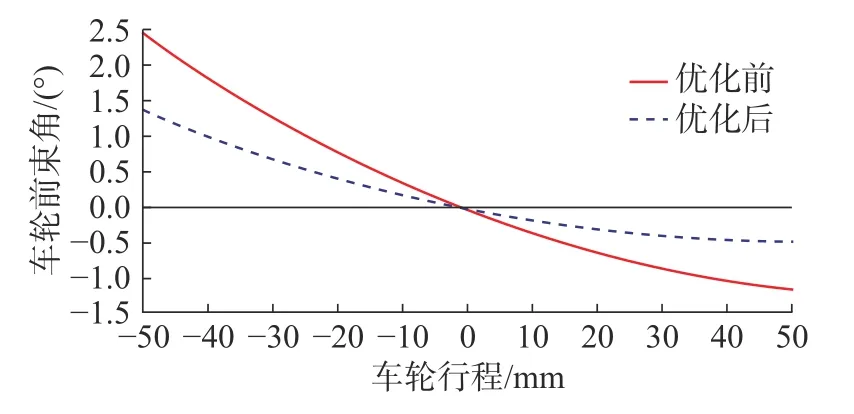
图8 优化前后车轮前束角变化曲线

图9 为优化前后主销内倾角变化曲线。结合图9 的仿真结果可得，主销内倾角的值由优化前的9.8°～ 11.6°变化到优化后的11.2°～ 12.6°，后倾角随车轮跳动其变化率减小，满足优化的目的。主要考察主销角度在设载状态下初值设置，主销内倾与后倾的变化趋势不做硬性要求。全行程下角度变化范围在2°以内。基础主销角度设置合理，因此优化主销角度参数也在合理范围内。

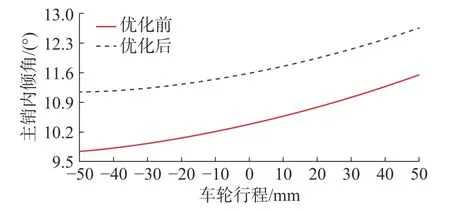
图9 优化前后主销内倾角变化曲线

4 结论

针对某SUV 双横臂悬架的结构特点，利用Adams Car 建立了双横臂前悬架模型。进行了相应仿真试验及硬点优化，得到以下结论：

1）通过平行轮跳试验仿真分析，分析该悬架的主销后倾角、主销内倾角、前轮外倾角、前轮前束值随车轮跳动的变化，精准确定了该悬架定位参数存在的问题。

2）利用Adams/Insight 模块，选择合适的硬点，对悬架硬点坐标进行优化。优化后的车轮外倾角和前束值在±50 mm 平行轮跳试验时的变化相比于优化前分别减小了29%和50%。优化后的主销后倾角和内倾角在仍满足要求的情况下，变化率均减小超过20%，悬架性能更加优秀。优化后的悬架能够满足车辆对于直线行驶稳定性、不足转向特性等性能的要求。优化设计满足了设计要求，悬架性能得到改善。

3）通过对虚拟样机的使用，实现对SUV 双横臂悬架的设计性能的检验，完成了对悬架的优化设计，虚拟样机的使用可以有效缩短整个产品的设计优化周期。