冗余驱动对3-PUS/S 并联机构的性能改善

史康，谢任远*,,2，余维,2，李德婷

（1.上海航天控制技术研究所,上海 201109；2.上海市空间智能控制技术重点实验室,上海 201109）

具有3 个转动自由度的并联机构是一类重要的少自由度并联机构。由于其自身的结构特性，具有常被应用于灵巧眼[1]、仿真转台、调姿平台、良好的一般工业及航天航空等军事工业应用前景，机械臂关节[2]等。许多学者对具有3 个转动自由度的并联机构，进行了构型创新设计与性能分析。

构型设计：史革萌 [3]对一种三自由度球面并联机构进行了瞬时运动学分析；Hemandez 等[4]提出一种腕关节球面并联机构，研究了其尺度综合；何延等[5]研究了一种三角化解耦并联机构，并进行了构型综合、运动学分析；Hou 等[6]提出一种3-PSS/S 球面并联机构；Wu 等[7]提出一种新型非对称的三支链球面并联机构，支撑高定位精度的移动平台。

性能分析：Enferadi 等[8]使用等效转角方法求得3-RRP 球面并联机构的刚度矩阵，分析了机构的刚度性能；Tao 等[9]采用最小干涉设计方法实现3-RRR球面并联机构工作空间的优化；杜力等[10]对一种新型的3T1R 并联机构进行了工作空间分析和尺度参数优化设计；胡波等[11]对一种非对称3-PRS 机构进行了运动等效和约束性能分析；赵裕明与金振林[12]提出了一类冗余三自由度并联机构，利用达朗贝尔原理进行了逆动力学模型并通过研究验证了其正确性。

冗余度机器人，分为结构冗余和驱动冗余，是指含有自由度数 （主动关节数）多于完成某一作业任务所需最少自由度数的一类机器人。冗余度机器人相对于一般并联机构具有更高刚度、更优的力操作性能和更大的承载能力等优点，目前已成为机器人研究与应用的一个热点[13]。为了改善机构的性能，一些学者尝试通过添加冗余驱动的支链来提升机构的性能。王晓明[14]提出了一种新型冗余并联驱动机构并对其奇异性进行了分析；Baron 等[15]研究了一种冗余并联机构规避奇异性的几何方法；Shin 等[16]分析冗余并联机构对并联机构刚度提升的影响，并根据分析结果做了优化设计；周结华等[17]对一种冗余三自由度并联机构进行了工作空间和奇异性分析；黄胜军等[18]提出了一种新型的三平移冗余并联机构并进行了相关的运动学性能分析。

上述文献表明了增加冗余驱动可以有效的改善并联机构性能。本文基于国内外目前三转动自由度并联机构的应用和发展，研究了两种相关的新型并联机构：3-PUS/S 并联机构和增加了一条冗余驱动支链的4-PUS/S 并联机构。主要通过对比分析，研究增加冗余驱动支链对原机构性能的影响。

1 构型描述与运动学分析

1.1 构型描述

3-PUS/S 并联机构包括动平台、定平台、一条中心支链以及对称布置于动、定平台之间的3 条结构相同的运动支链。3 条支链均依次由竖直导轨移动副、主动滑块、万向节、从动杆、球面副组成。在3-PUS/S 并联机构基础上增加一条和其他3 条支链对称布置的相同支链，便形成了冗余驱动的4-PUS/S并联机构。两种并联机构虚拟样机如图1 所示。

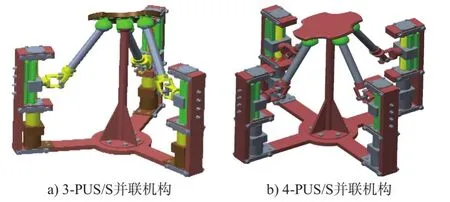
图1 两种并联机构图

1.2 机构自由度与相对自由度计算

3-PUS/S 并联机构含有动平台、定平台、主动滑块（3 个）、从动杆（3 个）等共8 个部件组成。由修正后的Grübler-Kutzbach 公式，计算可得

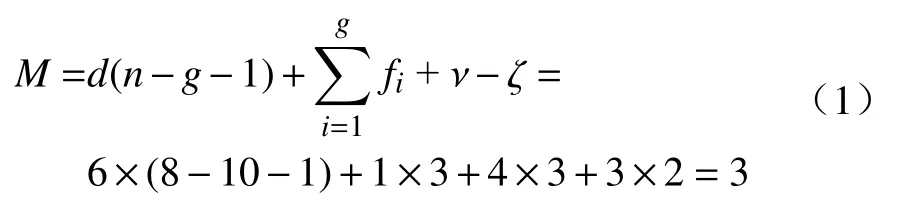
式中：M为机构自由度；d为机构的阶数；n为活动构件数；g为运动副数目；fi为第i个运动副具有的自由度数目；v为去除公共约束之后的冗余约束数目；ζ为局部自由度数目。

对于4-PUS/S 并联机构，同样由修正的 Grübler-Kutzbach 公式，计算可得

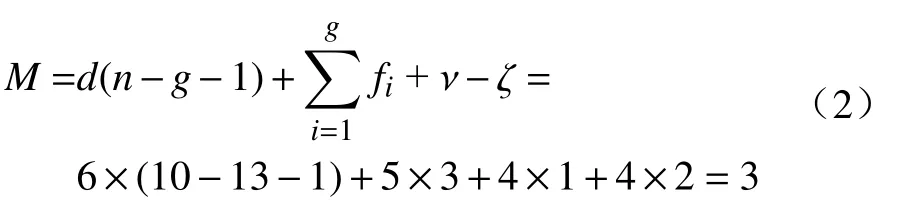
所以4-PUS/S 并联机构依然有3 个自由度，所加的驱动支链为冗余驱动支链。

相对自由度：机构动平台通过球副与基座铰接，确保机构动平台至多具有3 个转动自由度。而利用修正后的Grübler-Kutzbach 公式，可知机构自由度为3。所以，机构动平台具有3 个转动自由度。

1.3 机构运动学反解分析

运动学反解涉及已知动平台的位姿，求解各个驱动滑块的位移。本文所研究的两种三自由度转动并联机构，动平台由于受到与定平台相连的中心球副的约束，所以动平台中心位置固定，只存在姿态的变化，设动平台在坐标系中的3 个姿态角分别为α、β、γ。在两种并联机构中建立如图2 所示的坐标系。

图2 两种并联机构的坐标系建立图

设动平台3 个球副中心点依次为B1、B2、B3，令3 个球副中心点Bi到动平台中心点的垂直距离为r。3 个滑块上虎克绞中心点分别为A1、A2、A3。设虎克绞中心位置Ai到动平台竖直杆中心的垂直距离为R。以动平台中心处球副中心点O为原点建立定坐标系O-XYZ，Z轴竖直向上，Y轴垂直于A2A3，X轴由右手定则确定，设3 个主动滑块在Z轴的位置为hi。同样以O点为圆心建立固结于动平台的动坐标系M-xyz，M与O点重合，z轴竖直向上，y轴垂直于B2B3，x轴由右手定则确定。

用向量的形式表示出OAi和MBi，即：

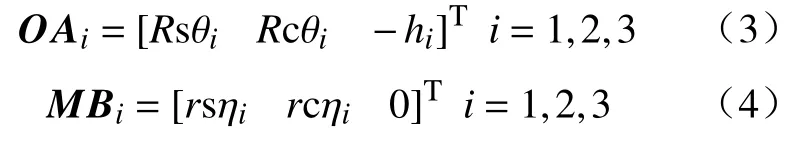
式中：s=sin、c=cos；θi为OAi在XY坐标平面上的投影与Y轴正方向的夹角，逆时针方向为正；ηi为MBi在xy坐标平面上的投影与y轴正方向的夹角，逆时针方向为正。

按照动坐标系先绕z轴旋转γ角、再绕y轴旋转β角、然后绕x轴旋转α角的旋转顺序，由动、定坐标系相对位姿，计算可得两者之间的转换矩阵为

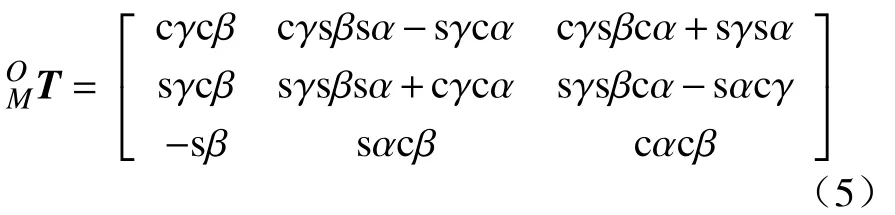
根据闭环矢量三角形方程和定杆长方程可得

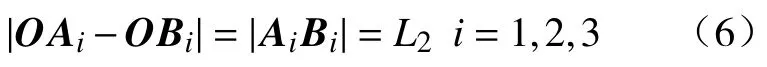
通过坐标变换等计算求得3-PUS/S 并联机构运动学反解通式为

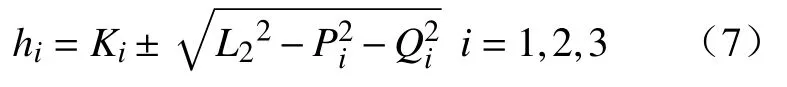
其中：

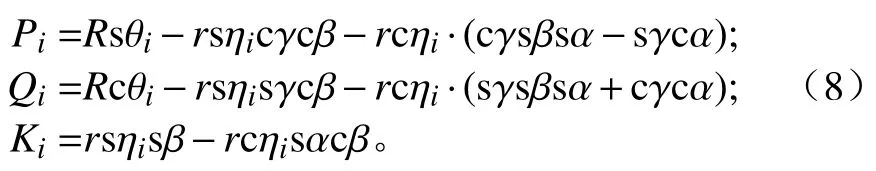
根据所建坐标系，代入 3-PUS/S 机构中已知量计算式（7）可求得其运动学反解依次为：

对4-PUS/S 并联机构进行同样的运动学反解分析。代入4-PUS/S 并联机构中已知量，计算式（7）可求得4-PUS/S 并联机构的运动学反解依次为：

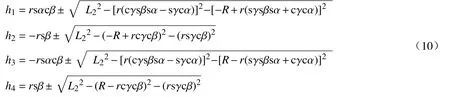
2 工作空间绘制与分析

2.1 工作空间搜索流程

基于两种并联机构的位姿反解模型及结构约束条件，采用离散边界搜索算法，使用工程软件，计算并绘制出机构的工作空间。采用的搜索算法流程如下：

1）根据机构设计要求，给定机构的结构参数：R、r，以及α、β、γ的搜索范围。

2）根据位姿反解模型计算出主动支链的长度hi。

3）检验此时支链长度hi状态下，是否满足由杆件尺寸、运动副转角限制等组成的边界条件。如满足，记录此时的α、β、γ值。

4）姿态角α、β、γ增加一个微小量后，继续搜索，直到搜索完设定好的整个α、β、γ范围。

5）将搜索过程中所有满足要求并记录的α、β、γ取值点绘制出来，形成整个机构的工作空间。

2.2 实例分析

给定机构参数如表1 所示。设定动平台姿态角α、β的搜索范围为（-0.6,+0.6）rad，γ的搜索范围为（-π/2,+π/2）rad。

表1 机构参数

按照上述流程图算法搜索出所有满足条件的α、β、γ。搜索并绘制出3-PUS/S 并联机构和4-PUS/S 并联机构工作空间如图3 所示，为了便于观察和比较大小，将两种并联机构工作空间在同一幅图里叠加显示如图4 所示。

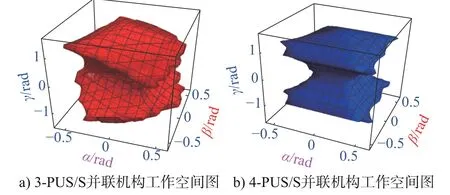
图3 两种并联机构的工作空间图

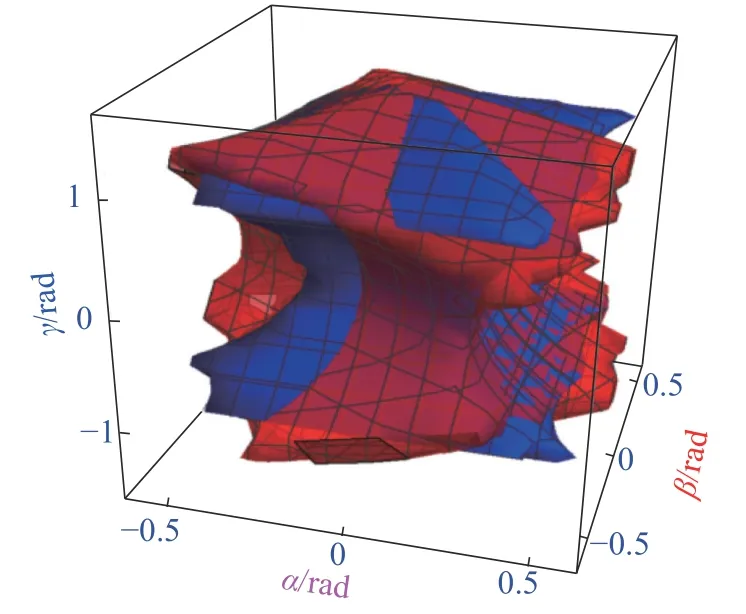
图4 两种并联机构的工作空间叠加图

通过观察发现，同等机构参数下，4-PUS/S 并联机构的工作空间范围略小于3-PUS/S 并联机构。可知在同等条件下引入冗余驱动支链，会略微减小原机构的工作空间范围，但并没有较大变化。

3 雅克比矩阵的求解

3.1 约束雅克比的求解

如图5 所示，在动平台中心处建立瞬时参考坐标系p-x′y′z′，3 个坐标轴方向分别对应平行于定坐标系的X、Y、Z并在此坐标系中表示后面提到的所有旋量。

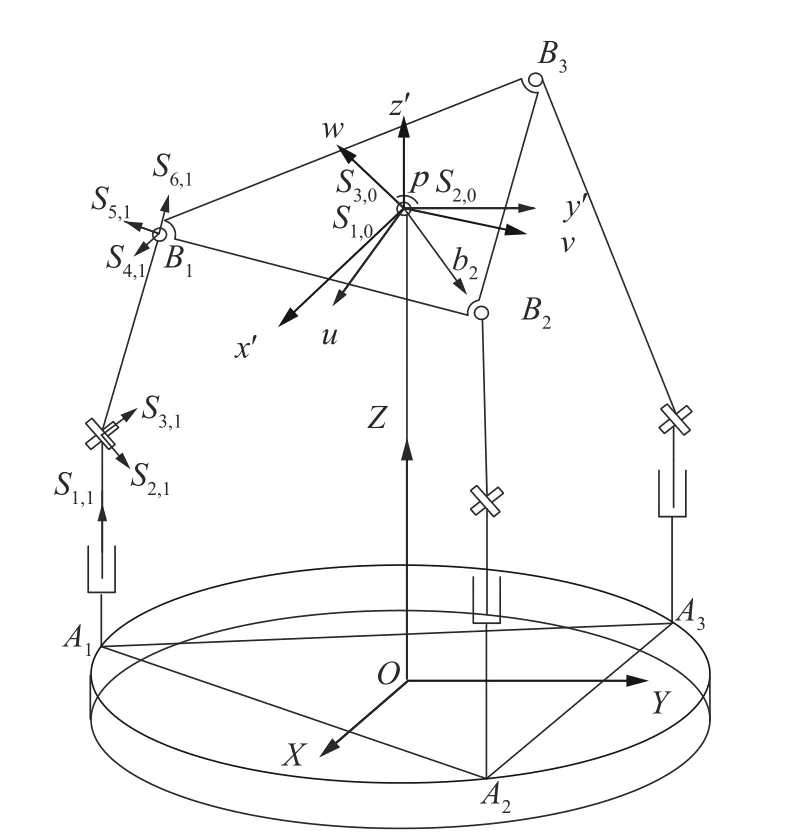
图5 3-PUS/S 并联机构示意图

由螺旋理论可知，动平台的瞬时螺旋S/p可表示表示：

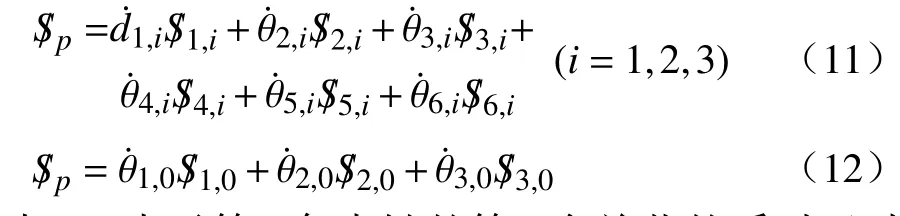
式中：S/j,i表示第i条支链的第j个关节的瞬时运动螺旋；表示第i条支链的第一个关节的移动速率；表示第i条支链的第j个关节的转动速率；表示中间约束S 支链第j个关节的转动速率；表示中间约束S 支链第j个关节的瞬时运动螺旋。

由图5 结合螺旋理论可知，各运动关节的瞬时运动螺旋表示：

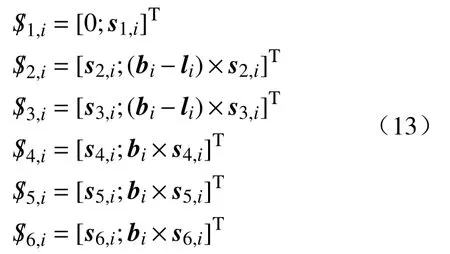
由螺旋理论可知，PUS 支链的6 个关节线性无关，自由度是6，所以没有约束反螺旋，对动平台不提供约束。中间约束S 支链中3 个运动螺旋表示为：

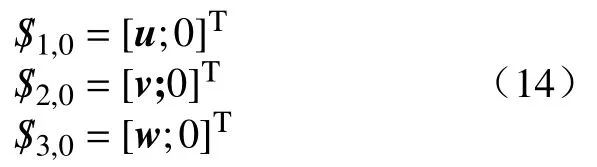
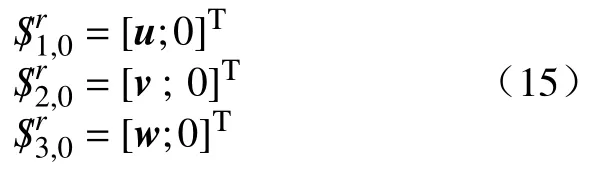
将此反螺旋系与式（12）两边作互易求积可得

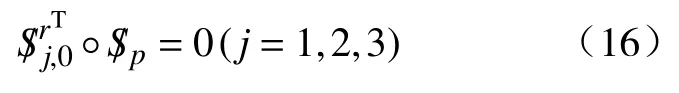
写成矩阵形式为：

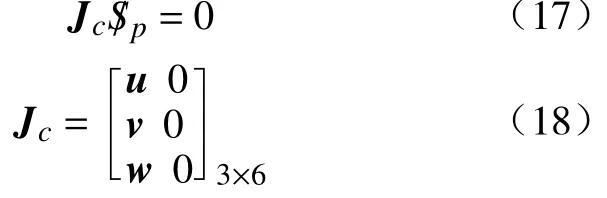
Jc即为所求的3-PUS/S 并联机构的约束雅克比矩阵。

3.2 驱动雅克比的求解

锁定每条支链中的驱动关节（移动副），由螺旋理论可知，此时每条支链增加一个反螺旋，可表示为

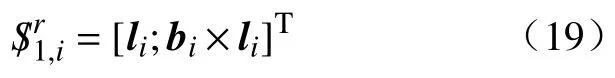
将此反螺旋系跟式（11）两边作互易求积可得

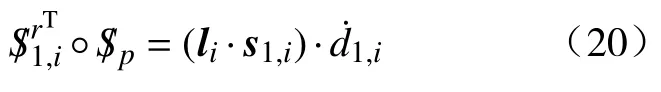
所以得到

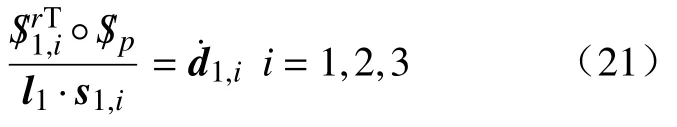
写成矩阵形式为：

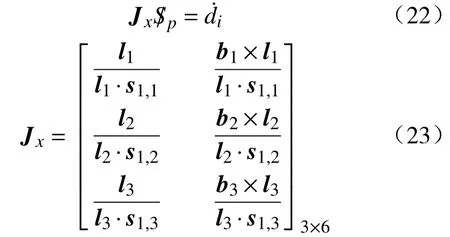
Jx即为所求的3-PUS/S 并联机构的驱动雅克比矩阵。

3.3 完全雅克比

综合Jc与Jx，即可得出3-PUS/S 并联机构的完全雅克比矩阵为

同样的方法，可求得4-PUS/S 并联机构的完全雅克比矩阵为

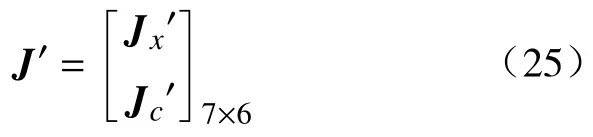
其中4-PUS/S 并联机构的约束雅克比矩阵为

4-PUS/S 并联机构的驱动雅克比矩阵为

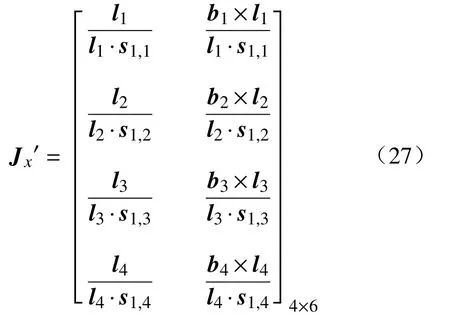
4 机构静刚度分析

当并联机构的结构参数确定后，机构的刚度会随着位姿的变化而改变，经常使用的衡量并联机构刚度特性的指标有刚度矩阵的行列式、特征值、条件数、迹等。这里使用刚度矩阵的最大特征值作为研究刚度的指标，对两种并联机构在相同结构参数下的刚度特性进行对比分析。刚度矩阵可以表示为

式中：J表示机构的雅克比矩阵；k表示驱动副的关节刚度，这里设定k=1000 N/mm。绘制出两种并联机构分别在γ=0、γ=π/4 时不同姿态下的刚度矩阵最大特征值分布图如图6 与图7 所示。

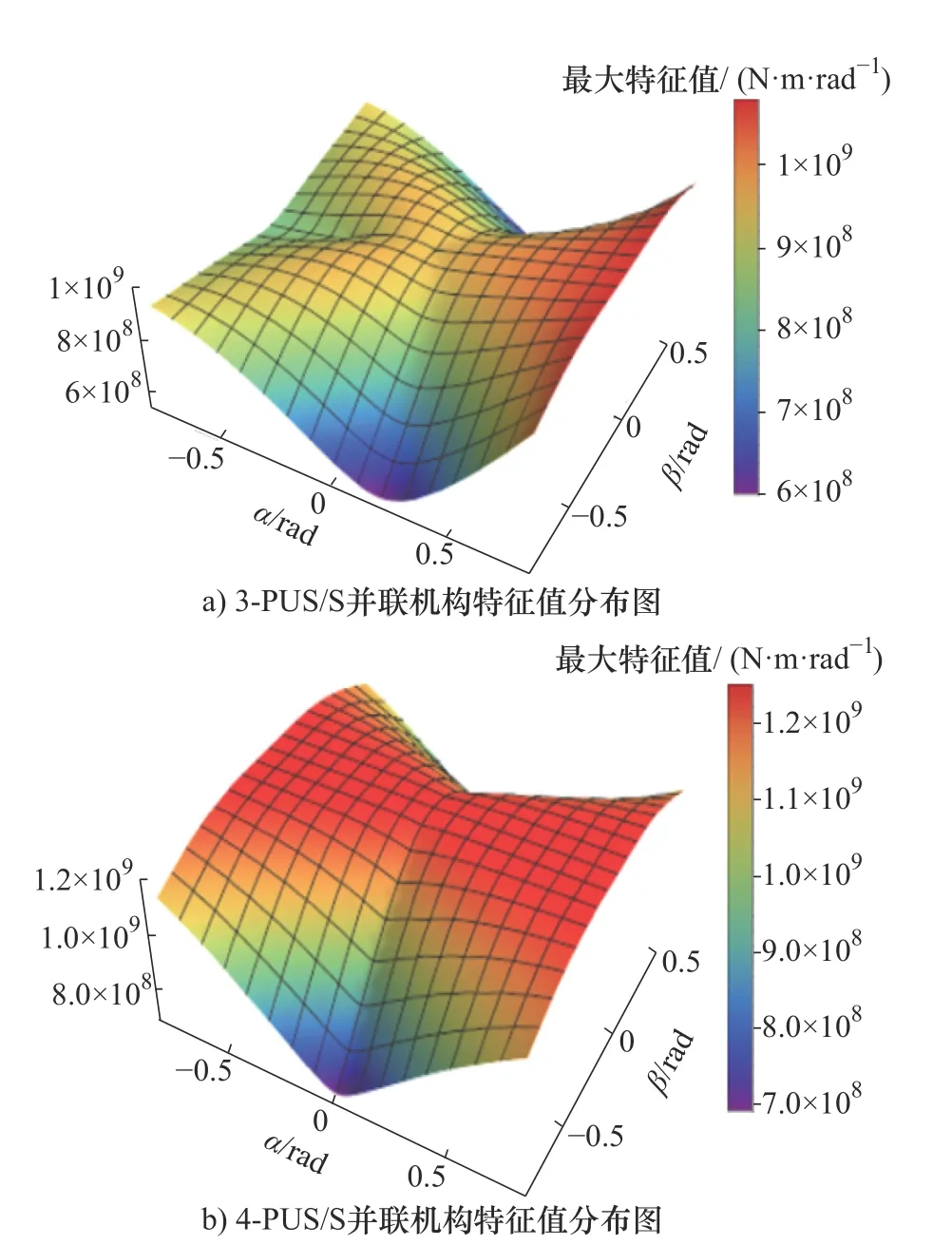
图6 γ=0 两种并联机构刚度矩阵最大特征值分布图

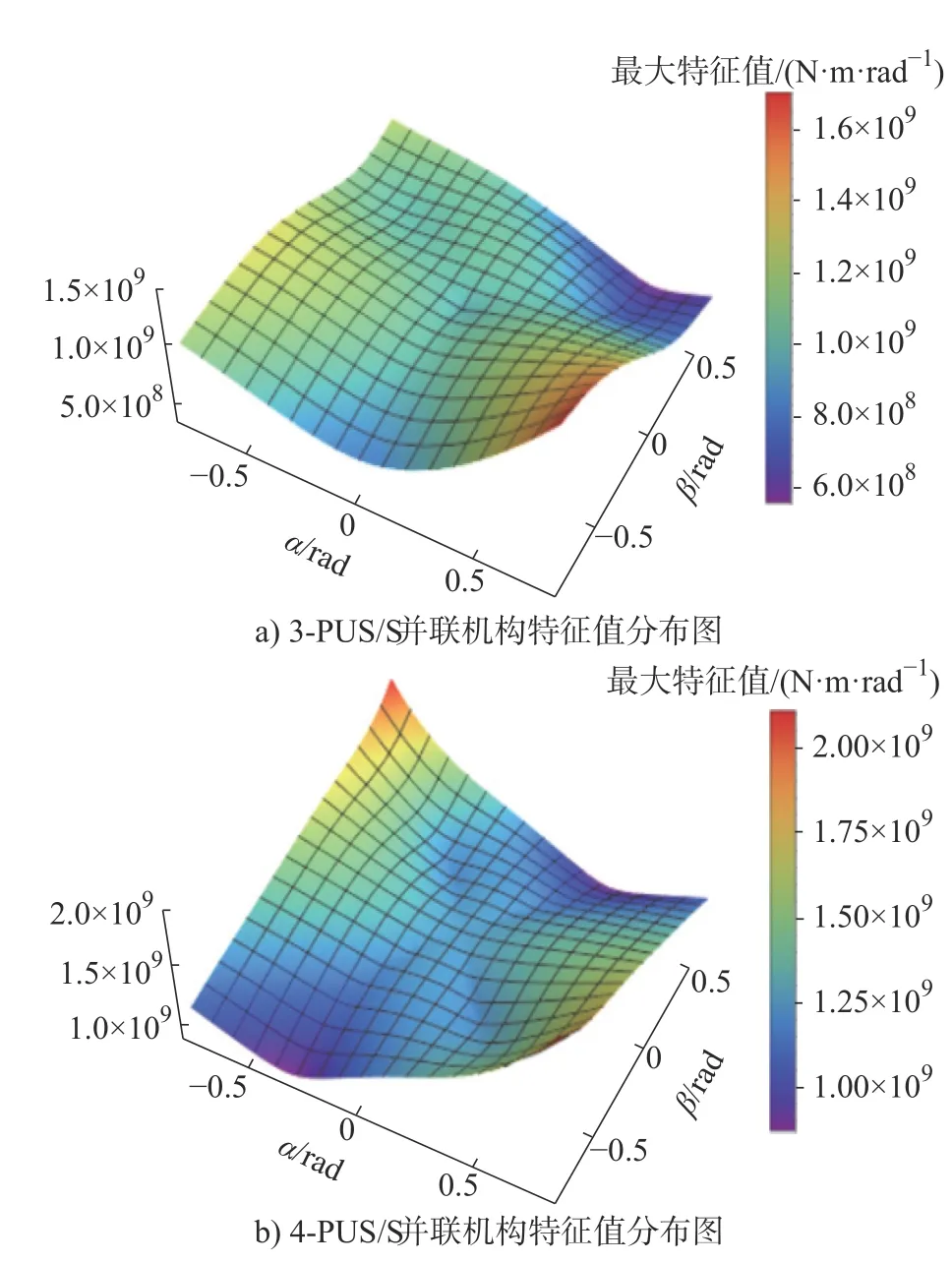
图7 γ=π/4 两种并联机构刚度矩阵最大特征值分布图

表2 给出了γ=0、γ=π/4 时两种机构的最大特征值数据对比情况。由表2 可知，γ=0 时，4-PUS/S 并联机构最大特征值相比3-PUS/S 并联机构总体提高了约20%，γ=π/4 时，4-PUS/S 并联机构最大特征值相比3-PUS/S 并联机构总体提高了约25%。

表2 两种机构最大特征值数据对比

说明出引入冗余驱动支链对机构刚度特性有一定程度的提高。从机构工作精度的角度考虑，引入冗余驱动支链降低了机构因受力变形引起的误差，提高了工作精度。

5 机构动力学分析

动力学的数学建模问题在三自由度并联机器人实际的运动控制和动态性能的分析中占有很重要的地位，三自由度并联机器人的动力学数学模型描述的是并联机器人的运动构件和各个关节力矩之间的关系，是求解机器人正向动力学问题和逆向动力学问题的基础。常用研究方法包括：拉格朗日法、牛顿-欧拉法、凯恩方法、高斯方法、旋量对偶法等。

本文将并联机构分为动平台子系统、从动杆子系统、主动滑块子系统等3 部分，拉格朗日方程为

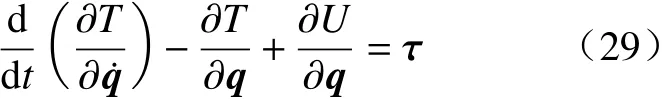
式中：T为系统动能；U为系统势能；q为广义坐标；τ为对应广义坐标q的广义力。

利用式（29）分别求解其动力学模型，最后求解出机构整体动力学模型。

本节以下求解公式中，选取广义坐标q=(α β γ)T，求解3-PUS/S 并联机构动力学模型时，i=1,2,3；求解4-PUS/S 并联机构动力学时，i=1,2,3,4。

5.1 动平台子系统的动力学模型

3-PUS/S 并联机构和4-PUS/S 并联机构均为绕动平台质心的三转动自由度机构，所以动平台无平动动能，只有转动动能。

动平台角速度为

动平台动能为

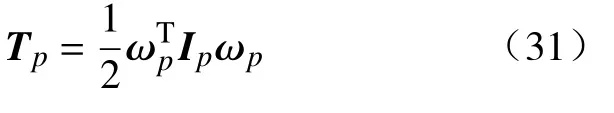
式中Ip为动平台转动惯量矩阵。

取动平台质心处水平面为零势能面，因为动平台没有平动，所以动平台势能为

将式（31）和式（32）代入到朗格朗日方程式（29）中，整理可得动平台子系统的动力学模型方程为

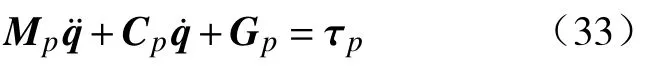
式中：Mp为动平台子系统惯性矩阵；Cp为动平台子系统哥氏力系数矩阵；Gp为动平台子系统重力项；τp为动平台子系统等效广义力。

5.2 从动杆子系统的动力学模型

动平台上Bi点的广义速率为

所以并联机构连杆A1Bi的角速度为

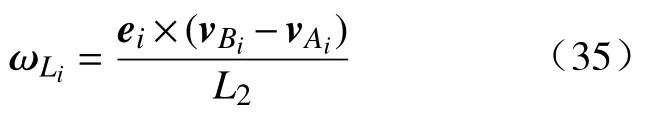
式中：ei为从动杆由点Ai指向点Bi的单位矢量；vAi为主动滑块的速度矢量。

由运动学基本知识知道，从动杆质心C的速度vCi为

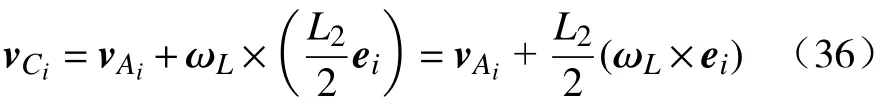
所以从动杆子系统动能

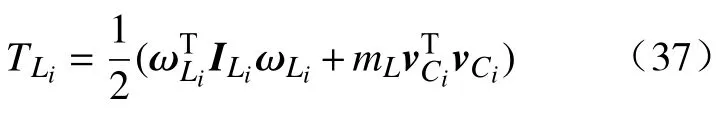
从动杆质心C的位置坐标可表示为

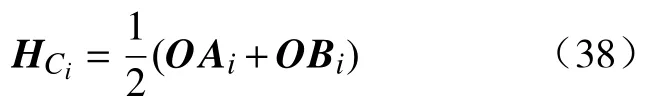
所以从动杆势能可表示为

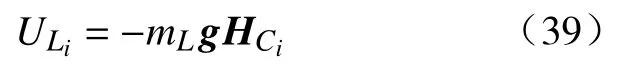
同理可得从动杆子系统的动力学模型方程为

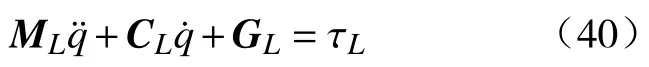
式中：ML为从动杆子系统惯性矩阵；CL为从动杆子系统哥氏力系数矩阵；GL为从动杆子系统重力项；τL为从动杆子系统等效广义力。

5.3 主动滑块子系统的动力学模型

主动滑块在丝杠上做直线运动，所以转动动能为零，其动能为

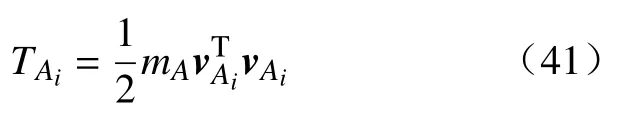
势能为

同理可得主动滑块子系统的动力学模型方程为

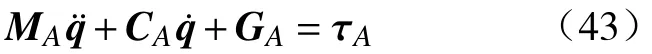
式中：MA为从动杆子系统惯性矩阵；CA为从动杆子系统哥氏力系数矩阵；GA为从动杆子系统重力项；τA为从动杆子系统等效广义力。

5.4 机构整体动力学模型

在求得机构各子系统动力学模型的基础上，可以得到整体动力学模型为：

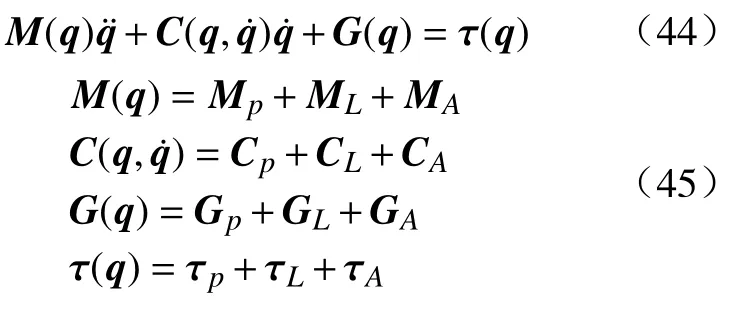
由虚功原理可知，3-PUS/S 并联机构的关节驱动力和等效广义力之间的关系为

式中：J为3-PUS/S 并联机构的雅克比矩阵；F=(f1f2f3)T，为关节驱动力。

在4-PUS/S 并联机构中，由于机构有3 个自由度，4 个驱动，所以机构在任一状态下都有无穷多组驱动力的解，根据虚功原理和范数最小原则确定此机构关节驱动力和等效广义力之间的关系为

式中：J为4-PUS/S 并联机构的雅克比矩阵；(JT)+=J(JTJ)-1,为JT的伪逆；F=(f1f2f3f4)T，为关节驱动力。

5.5 动力学仿真结果分析

在上述动力学理论计算的基础上，选定机构设计参数，进行实例验证。设定机构参数如表3 所示。

表3 机构参数

规划动平台运动轨迹函数为：

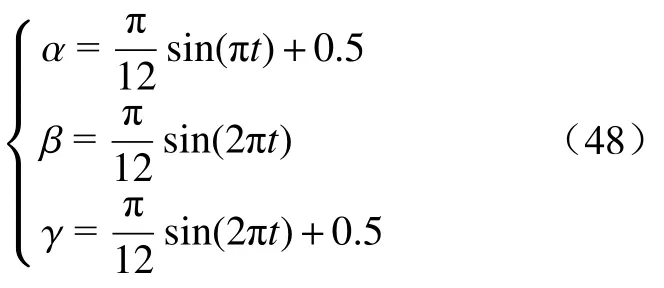
根据已求得的动力学方程，可求得两种并联机构各主动滑块的驱动力，绘制10 s 内两种并联机构各主动滑块驱动力曲线，选取其中曲线较为平滑的2～10 s 区间段如图8 所示。图中f1、f2、f3、f4分别代表两种并联机构各主动滑块的驱动力。

图8 两种并联机构驱动力曲线图

由两种并联机构驱动力曲线对比可知，动平台在此种运动规律状态下，驱动力曲线平滑无突变，说明机构运行良好，没有出现奇异位置。添加了冗余驱动支链的4-PUS/S 并联机构相比于3-PUS/S 并联机构，各主动滑块驱动力峰值总体呈下降趋势，降幅为30%左右。但相应的，各驱动力的最小值总体上升了25%左右。总的来说，在添加了冗余驱动支链后，机构驱动力配置效果更加高效，改善了并联机构的驱动性能。

6 结论

本文研究了一种3-PUS/S 并联机构和4-PUS/S 并联机构，并对这两种并联机构进行了运动学反解模型的求解、工作空间的绘制与对比分析、完全雅克比矩阵的构建、静力学刚度矩阵的分析、动力学模型的建立与分析、探究引入冗余驱动支链对原机构性能的影响。

由两种机构的理论分析以及仿真结果对比可知，引入冗余驱动支链对原并联机构性能的影响与预期相符，得到了引入冗余驱动支链对原机构动平台的工作空间范围有略微减小、在一定程度上改善了刚度特性分布情况、提高了机构刚度、工作精度、改善了并联机构驱动性能等的结论，为后续研究两种并联机构的控制及应用奠定了基础。